3.1.3 移动边界模型
137Cs进入土壤表层之后的再分配是一个复杂的综合作用过程,包括物理、化学和生物作用[181184],影响137Cs再分配过程的因素包括土壤属性、地形和土地利用等[185-190]。137Cs再分配模型多数建立在没有侵蚀作用条件下,其中包括对流-分散模型[15,178,191,192]、分隔模型[193-195]和其他模型[196]。剖面分布模型和扩散模型都是基于137Cs再分配原理进行建模,扩散模型相对于剖面分布模型考虑更为全面。扩散模型主要包括传输模型[169]和简化传输模型[179]。传输模型建模虽然充分考虑了137Cs再分配的多个环节,但是模型结构复杂,参数较多,很难应用到实际研究中。简化传输模型结合前人研究成果,忽略扩散方程的对流项,极大地简化了计算过程,提高了模型的实用性,具有很重要的科学意义。
模拟侵蚀条件下137Cs扩散过程比较复杂,难点主要包括两点:①扩散的上边界(土壤表层)会随着侵蚀向下移动;②边界处在侵蚀作用下,137Cs向系统外部流失,影响系统内部的扩散。简化传输模型假设侵蚀只发生在每年年底较短的时间内,忽略侵蚀过程对侵蚀表层以下土壤137Cs扩散的影响,模型特别适用于年降雨量少,且降雨集中的地区,但是对于雨季较长,月降雨平均的地区该模型具有一定局限性。本书旨在简化模型基础之上,借助地球化学动力学移动边界问题的解决方法,完善该模型。
3.1.3.1 模型建立
模型采用张信宝教授的两点假设:①不考虑对流作用;②初始条件为瞬间面源,即在初始时刻(1963年)137Cs以总质量M以极高的浓度集中于x=0处,浓度视为无限大。未侵蚀剖面在固定于实验室的参考系中土壤剖面中137Cs扩散方程可以描述为
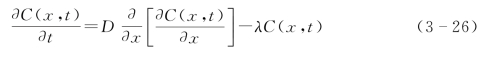
侵蚀剖面中的137Cs的扩散,可将土层视为半无限介质,如图3-2所示。
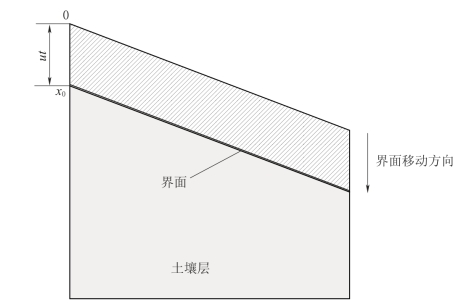
图3-2 侵蚀剖面的扩散移动边界
图3-2中,在t=0时刻,土壤与空气的界面为x=0处,表层经过时间t侵蚀作用移动到x 0处,即移动边界。假设移动速度(侵蚀速率)为u,本章假设移动速度为恒速。侵蚀过程中,边界向下移动。界面位置与时间的关系为
![]()
为了便于下文讨论边界处的物质迁移,需要对坐标系进行转换,即由实验室固定参照系转为界面固定的参照系。在新的参照系下,坐标用y表示,且两相(空气和土壤)界面固定于y=0处。具体的变换为

将式(3-27)和式(3-28)代入式(3-26),变换新参照系下的扩散方程为
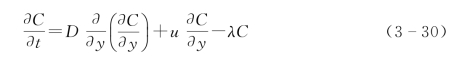
式(3-30)与式(3-18)相似,但是它们有着完全不同的物理意义。式(3-18)中V代表对流项的达西流速,式(3-27)中u代表侵蚀速率,且两个方程的坐标系是不同的。改变坐标系后微分方程t=0时刻初始条件没有发生变化。
![]()
界面y=0的组分通量为

边界处137Cs吸附的黏土颗粒随雨水以泥沙形式带走,可看作与热传导一维杆在边界处与移动的流体(例如空气)接触时扩散的相同问题。这种情况第一类边界条件或者第二类边界条件都不合适,需要用到第三类边界条件(牛顿冷却定理),即在边界处,流出杆的热流近似地与杆和外部的温差成比例,同理,则在左端点(y=0)处,137Cs损失的组分量为
![]()
C B(t)表示外部空气中137Cs的浓度,在这里C B(t)=0。这里需要特别注意u>0,且u前面的符号为负号,本文扩散为半无穷介质,不存在右边界,只有左边界。如果为有限介质内的扩散,右边界处u前面的符号要取正号。137Cs损失的组分量式(3-33)应当与扩散通量式(3-32)相等,即

3.1.3.2 模型解法
式(3-30)中λC为衰变引起的浓度变化,放射性组分的扩散方程需要先对方程两边同时乘以eλt,简化模型,消去衰变项,式(3-30)变换为
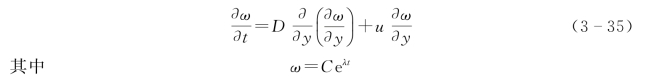
综合以上,土壤侵蚀剖面137Cs扩散模型如下:
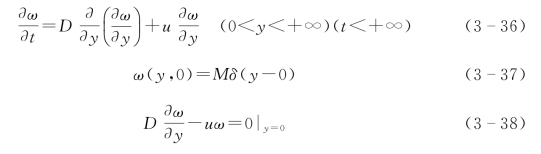
为求解式(3-36)~式(3-38),需要先去掉式(3-36)中一阶项![]() ,为此令
,为此令
![]()
其中a,b为待定常数。
对将K代入,对y和t求导
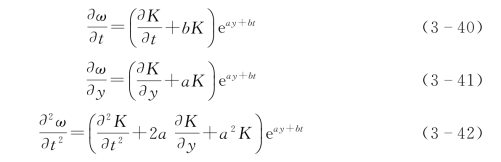
将式(3-40)~式(3-42)代入式(3-36),消掉e ay+bt
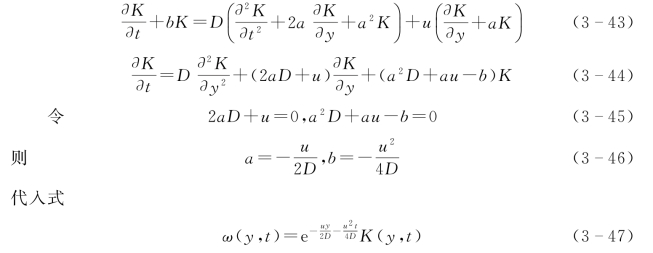
由上面公式可知K(y,t)应满足方程:

K(y,t)应满足的定解条件为
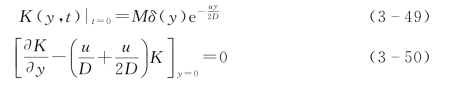
由数理方程知
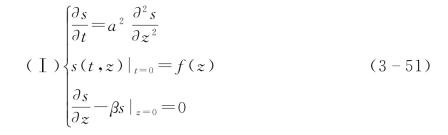
上式的求解公式为
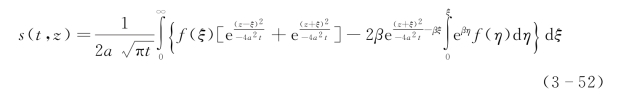
由此可得式(3-48)~式(3-50)的解为
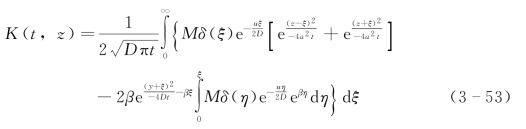
其中,![]() 。
。
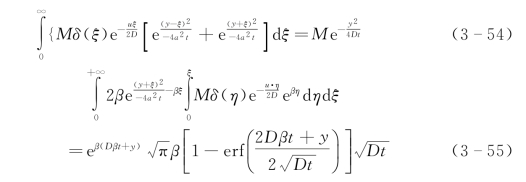
将式(3-54)和式(3-55)代入,利用式(3-39)将K(t,z)替换为ω(y,t),再根据ω=C eλt,得到的最终结果为

式(3-56)两边对x求积分,结果为
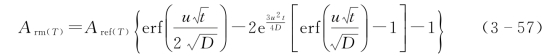
式中 A rm(T)——剖面剩余137Cs面积比活度;
A ref(T)——取样年份137Cs面积比活度背景值。
3.1.3.3 讨论
令侵蚀速率u=0,即在非侵蚀条件下137Cs剖面浓度变化,方程可以简化为
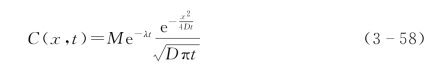
式(3-58)与简化扩散模型非侵蚀条件下解相同式(3-23)。若侵蚀速率u≠0,式(3-56)可以分为两部分:式(3-59)和式(3-60)。
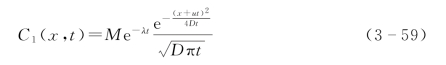
C 1(x,t)可视为C(x,t)向上平移u×t个单位。
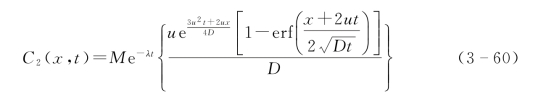
式(3-60)中令t和u保持不变,观察C 2(x,t)随深度增加的变化趋势,如图3-3所示,图中C 2(x,t)在表层取最大值,随深度增加以指数形式减小。
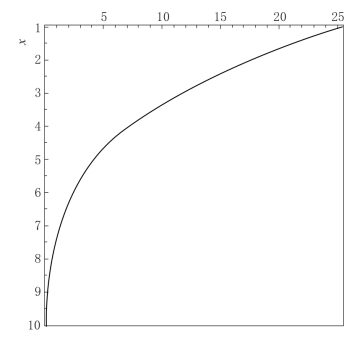
图3-3 137Cs浓度变化曲线
如果忽略边界位置137Cs通量变化对其本身扩散的影响,则C 1(x,t)则可以近似看做在侵蚀条件下137Cs浓度随时间和深度变化的分布函数,即非侵蚀分布函数式(3-58)向上平移u×t个单位。如果在雨量充沛的地区,侵蚀作用较长,必须考虑边界条件,C 2(x,t)可看做通量变化对表层以下137Cs浓度的影响因子,表层部分所受影响最大,浓度减少最大,随深度增加以指数形式减小。综上所述,C 1(x,t)-C 2(x,t)构成了在雨量充沛地区,侵蚀条件下137Cs扩散方程的完整解。
3.1.3.4 模型验证
式(3-56)和式(3-57)提供了两种获取侵蚀速率的方法。式(3-56)可通过不同深度137Cs浓度值进行曲线拟合直接获得侵蚀速率和扩散系数。图3-4为样点剖面137Cs浓度分布,样品于2013年采于贵州省遵义市新浦镇附近未干扰林地山顶。面积比活度为504Bq/m2,该区域的2013年的本底值为802Bq/m2,1963年的本底值为2497Bq/m2,137Cs衰变常数取0.0227,将图3-4数据和相关系数代入,使用MATLAB进行曲线拟合,如图3-5所示。获得扩散系数D=0.54,侵蚀速率为0.034,曲线拟合指标R 2为0.92。
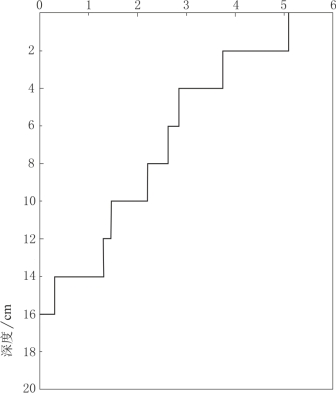
图3-4 采样点137Cs浓度分布图
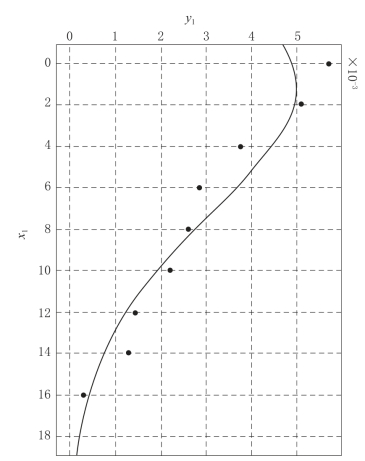
图3-5 模型曲线拟合结果
使用式(3-57)计算侵蚀速率需要先通过背景值剖面获取扩散系数D。为了对比与简化传输模型之间的差异,本章使用2004年开县数据[179],扩散系数D取1.98cm2/a,得到在不同损失率下的侵蚀速率,表3-1列出了模拟结果对比。
表3-1 模拟结果对比
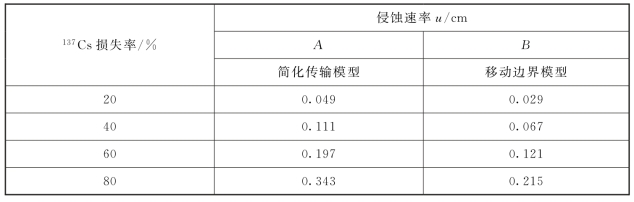
如前文所述,在年降雨充沛的地区,简化传输模型得到的侵蚀速率会大于实际值,本文移动边界侵蚀模型在相同137Cs损失率的条件下结果均小于前者,约为前者的60%,结果符合预期。
