五、基本集合对十二音和声的控制

一、前言

十二音作曲法的实质是它的和声问题。

从30年代到70年代的整整四十年里，西方理论家对十二音和声问题一直争论不休。对勋伯格十二音作品中的和声持怀疑态度的一派主要提出两个问题：（一）不协和音问题；（二）作品的一体化问题。关于第一个问题，勋伯格早在《和声学》（1911年）中用“远关系泛音”的理论，后来又在《用十二音作曲》（1941年）中用“不协和音的解放”的理论已经作出回答；争论的焦点便转移到第二个问题。怀疑者们认为：调性体系可以控制作品的横向面与纵向面（即旋律与和声）并使之一体化，而十二音体系则只能控制作品的横向面，因而不可能产生一体化的音乐结构。他们主要的根据是：十二音音乐中所有各种“例外”的处理如重复、序列的重新排列、截段的纵向结合、非毗邻截段的横向结合等等，都有可能产生与基本集合[2]无关和无法解释的和声。

在自由无调性时期，这种结构功能不明确的和声确是存在过。勋伯格自己说过：在调性作品里，和声是为发展曲式服务的，好比文章结构中标点符号对于构成句子、分段与合成章节的作用，而新的无调性方法，虽然同样需要发展曲式，却“几乎不能把希望寄托在这些结构价值尚未弄清的和弦上。因此，最初想写出结构复杂或篇幅很长的作品几乎是不可能的。”（《用十二音作曲》第三段）自从找到了十二音方法之后，情况便发生了根本变化，不仅他音乐中的旋律来自基本集合，而且某些更重要的东西也来自基本集合，“其规律性和逻辑性完全比得上早期的（调性）和声。”[3]（《用十二音作曲》第五段）既然勋伯格已作出如此明确的结论，为什么怀疑者们还要不断著书撰文去曲解（当然并非恶意）勋伯格的十二音和声呢？归根结底，无非两个原因：（一）他们没有真正了解勋伯格的十二音和声或基本集合的实质；（二）勋伯格本人的辩词仅仅停留在理论上的反驳，在他的讲稿中虽也举出不少自己早期的作品来说明他的写作方法，但未用完善的分析方法去对他的和声作进一步的论证。

著名音乐理论家阿伦·福特（Allen Forte）在他1973年出版的《无调性音乐的结构》一书中，应用集合论的原理，创造出一套分析无调性和声结构的方法。1977年，他的学生，理论家马塞·海德（Martha· M·Hyde）继而写出一本专著《勋伯格的十二音和声》，运用她老师的理论去对勋伯格的《组曲》Op.29作深入细致的解剖，为我们了解勋伯格的十二音和声提供了很有价值的参考资料。

到底什么是勋伯格“正宗”的十二音和声呢？它的规律性和逻辑性果真比得上调性和声吗？这便是本文所要讨论的问题。

二、基本集合与勋伯格的十二音和声概念

勋伯格之后，一些西方的有关论著常把十二音列称为“序列”（Se⁃ries）。值得注意的是，勋伯格本人在他所有的英文著作中却一律把十二音列称为“基本集合”（basic set）。事实上，“序列”一词只反映出十二音列的表面形态，即十二个有定序的音级（pitch-class，）；而“基本集合”这个术语才真正反映出十二音列的实质，即音与音之间的内在联系。这个术语显然与数学的集合论有关，而用集合论的原理去演绎十二音列的结构问题是最有说服力的。

在《用十二音作曲》中，勋伯格提出许多与他的十二音和声概念有关的论述，归纳起来，大致有以下三个方面：

第一，这种作曲程序是建立在基本集合不断反复使用的基础上的。作为所有旋律及和声的写作材料，基本集合在十二音音乐中的作用相当于调性音阶在调性音乐中的作用。基本集合还起着主题的作用，因而每个作品都必须有自己独特的基本集合；但它又有别于调性音乐中的那种主题，在实现其作为主题（或动机）的功能时，是不依赖于节奏、句法等外部特征的。

第二，基本集合中任何三至九音的线性截段[4]都代表这个基本集合的和声（一般不称作“和弦”）。如将一个基本集合分割成为两个截段，这两个截段便为互补关系，即互为“补体”（complement）。二音截段不足以代表基本集合的和声，因为它只包含一个音程，未能体现出最低限度和声结构；十音截段也不能作为和声单位，因为它的补体是二音截段。所有具有和声意义的三至九音的线性截段都是基本集合的子集合（subset，简称“子集”）。

一个截段（集合）一旦被用在作品中并且具有和声意义，其特征便不是由音级内涵或排列的次序来决定，而是由它的音程内涵来决定。好比在调性音乐里，当一个大三和弦在旋律中作横向呈现时，它的音级内涵或排列是不重要的，三音可最先出现，然后再出现五音和根音，或作移位处理，人们都会听出是大三和弦，因为它的音程内涵始终是大三度、小三度和纯五度或其转位。

勋伯格说：“当基本集合己被耳朵熟悉之后，在作品后面部分可以容忍稍稍偏离这个次序。但在作品开始时不应有所偏离。”（《用十二音作曲》第九段）这既为严格遵守基本集合的次序作了原则性的规定，也为必要的“例外”提供了理论根据。

第三，勋伯格把十二音音乐的织体（和声）看作是一个多维的音乐空间（musical space）即多面体。在这个多面体中，横向面和纵向面都受基本集合的控制，都代表着基本集合的和声[5]，它们之间具有高度的同一性；这种同一性在调性音乐中同样存在，只是在十二音音乐中表现得更为突出而已。由于这个多维空间里的所有的“面”（纵向的与横向的）都来自同一个基本集合并受这个基本集合的严格控制，故其和声结构是完全统一的。

勋伯格的十二音和声概念，是了解他的十二音和声的先决条件，但进入具体分析，还得借助于阿伦·福特关于分析无调性音乐[6]结构的方法；而福特的方法又集中反映在他所编制的《音级集合原型与涵量表》（简称“集合表”，见附件）里。福特将所有可能的三至九音的音级集合（原型）按“集合名称”（Name）、“音级内涵”（pcs）和“音程涵量”（Vector）三个项目及互补关系相对照的方式编制成表，为我们的分析提供了十分方便的工具。简介如下：

第一项——集合名称：

例如表中第四行的“3-4”，其中3表示该集合是一个三音组，4是该集合在所有三音集合中的编号。这样，“3-4”便代表某一特定的三音集合，好比调性和声中的和弦标记。

第二项——音级内涵：

八度内的十二个音（包括不同音区）分别用0至11来表示它们的音级（12=0）：0代表C、^♯B、^♭♭D；1代表^♯C、^♭D；……11代表B。“3-4”的音级内涵是“0，1，5”，意味着它的原型由C、^♯C、F组成。

第三项——音程涵量：

如以四音集合“4-4”为例，其音级内涵为“0，1，2，5”，可用以下方法求出其音程涵量为〔211110〕：

先求第1音与第2，3，4音之间的音程量；再求第2音与第3，4音之间的音程量；最后求第3音与第4音之间的音程量。代表音程量的数字表示该音程的半音数——1为半音，2为全音，3为小三度，4为大三度，5为纯四度，6为三全音，而大于三全音的音程一律折换成较小的转位音程。然后，作一次统计，〔211110〕表示这个集合包含有2个半音，1个全音，l个小三度，1个大三度，1个纯四度，0个三全音。

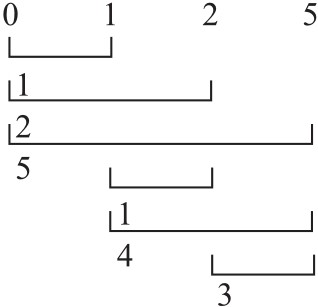
一个集合的音程涵量愈小，其补体的音程涵量愈大，反之亦然。以上这个“4-4”及其补体“8-4”（见表中同一行的右方）的音程涵量的关系是：

在“音程涵量”的前五项数中，“8-4”总是比“4-4”大四个数，而第六项则只大两个数，仅及前五项的一半。这是因为，在八度内的所有各种音程中，凡大于6的音程都已折换成为小于6的音程（11=1， 10=2，9=3，8=4，7=5），而6不能折换，因此，6以外的音程都比6多一倍。从这里可看到，两个互补集合相对应的项之间的差，与集合之间大小的差（即集合名称第一个数字的差）相等。这种音程的比例性，使我们有理由把一个集合的补体看作是该集合的缩小或扩大的重复；这样，互补关系的集合，彼此之间的关系便建立在一个牢固的基础之上。

表中有少数集合名称的编号附加有字母“Z”，这是表示，除这个集合之外，还有另一个集合与它具有相同（等量）的音程涵量，但又不能简化成为相同的原型。例如“4-Z15”与“4-Z29”便是一对具有这种关系的集合：

例1

这张集合表上只列出各集合的原型，不包括它们的移位及倒影。

原型的移位，因其形态与原型完全相同，可简单地将其音级折换成与原型相同的音级。

例如：一个音级内涵为“7，8，0”的集合（见下例b），可将其音级改记作“7，8，12”，再将最低音“7”作为“模”数，每个音级都减去7，结果可还原成为原型“0，1，5”。

再例如“3-4”的移位倒影“8，0，1”（下例c），因其形态不同于原型，只能简化成“0，4，5”而无法折换成与原型相同的音级内涵，但其音程涵量仍与原型相等。

例2

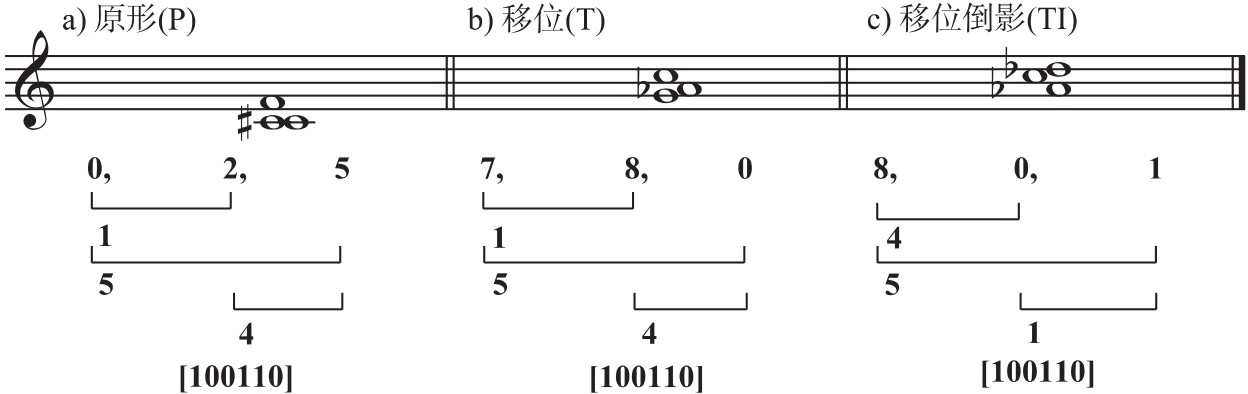
注：P为Prime的缩写，与O（Original的缩写）通用。T为Transposition的缩写。

三、基本集合对十二音和声的全面控制

下面我们借助于福特的“集合表”来分析几个勋伯格早期十二音作品的例子[7]。在十二音织体中，常见的序列音分配方式有所谓“纵横法”、“分割法”和“重叠法”三大类型；以下选择的例子便分别属于这三种类型。

（一）纵横法的例子：

例3（见下页）

所谓“纵横法”，就是让序列音按时间先后依次出现，同时体现在织体的纵向与横向的关系上，各声部发音点基本上被错开，这种类型常见于二部或二部以上的复调织体。

上例由单一序列形式（P）作三次反复构成，织体包括三个“面”。第一面是它的整体，也就是通常所说的纵向面，由于基本集合严格地呈现三遍，它已展示出基本集合的全部和声。第二、三面是两个横向的对位声部。大管声部最初出现了两个线性截段，即2~5号音和8~11号音（有句逗相配合），其pcs都是“4-21”，它们都代表基本集合的和声。接下去的旋律由一些非毗连音级组成，直至第6小节又出现一个线性截段（pcs4-2）。这些非线性截段表现为八个相交迭的，与线性截段等量的三音集合“3-8”“3-2”“3-1”“3-6”（请与该例下端的图解相对照）。最后一个非线性截段（pcs3-7）与线性截段“9-7”（2~10号音）互补，也同样代表基本集合的合法和声。这个和声面直接表现为线性截段的虽为数不多，但由于作者的巧妙安排，通过等量和声的关系与基本集合挂上了钩；这正好证明“和声不是由音级或排列来决定，而是由音程内涵来决定的。”再看圆号声部，头两个三音集合虽为非线性截段，但分别为pcs“3-7”和“3-8”，与线性截段等量；尤其值得注意的是，整个圆号声部一共只出现十二个音，包括基本集合的所有音级和序数，它的排列具有一定的规律性。

例3 勋伯格：《木管五重奏》Op.26

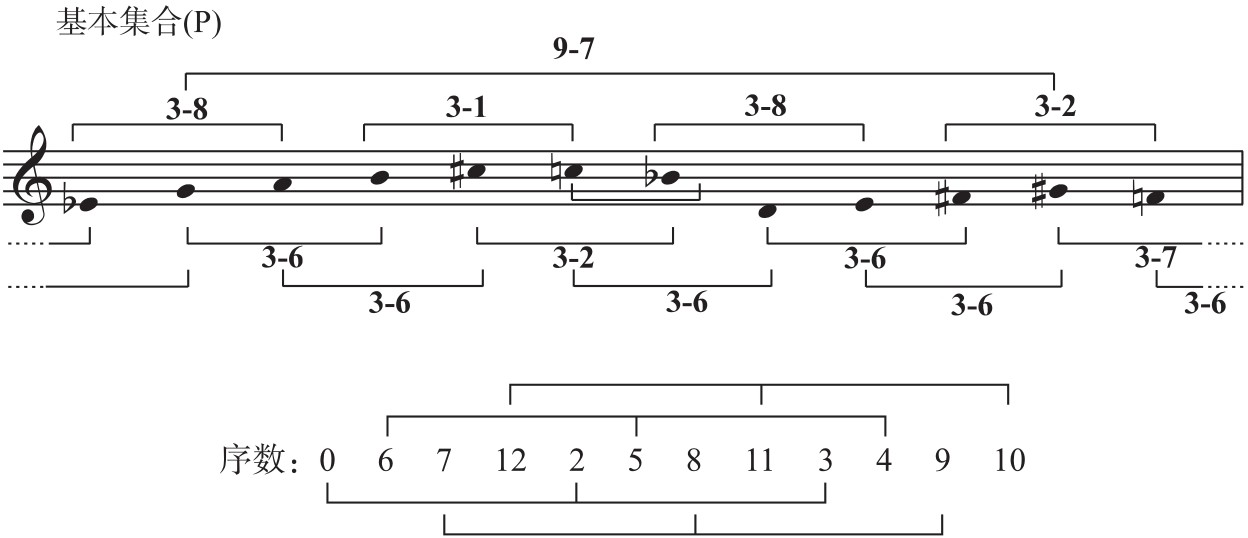
下一个例子同样属于“纵横法”，其和声结构表现得更加严格：

例4 勋伯格：《管弦乐变奏曲》Op.31

“第VI变奏”

基本集合（I₆）本身具有隐伏二声部的性质（见上例下端图解），织体中“隐伏”声部“公开”化，被写成两个对位声部。纵向面与例3一样，全由基本集合所控制。值得注意的是，两个横向面由四个与线性截段等量（“3-4”“3-5”“3-1”）的非线性三音截段组成，这就充分体现出基本集合对这段音乐的所有和声面的控制。

（二）分割法的例子：

例5 勋伯格：《钢琴组曲》Op.25

所谓“分割法”，就是将一个基本集合分割成若干个截段并将它们用于不同的声部或层次。

例5便是将一个单一的序列形式（P）分割成为a、b、c三个截段。a被作为和声背景，b、c被写成两个对位旋律。音组c（序数9~12）在音组b（序数5~8）尚未结束之前的插入，似乎打乱了基本集合的顺序，但却是合乎逻辑的。因为：（1）“间奏曲”是《组曲》的第四曲，这时基本集合已被人们所熟悉，必要时作一些适当的“偏离”是允许的；（2）分割的线性截段有时可以作为独立的小集合而发挥作用[8]；（3）两个旋律相结合的结果，又构成两个表现为小分句（有明显的音型及句逗）的新的和声结构面——“4-18”和“4-5”，它们都与基本集合的线性截段等量；（4）作为三个分割截段相结合的完整织体（纵向面），已表现为线性截段“4-5”与“4-18”的补体“8-5”与“8-18”（对照上例图解）。于是，这段音乐处处都受到基本集合的控制。

再看勋伯格《组曲》Op.29的一个例子。这里分割截段被排列成为纵向的和弦：

例6 勋伯格：《组曲》Op.25

整个织体的纵向和声是四个结构为“3-3”的和弦的并列，这是直接来自基本集合的和声，不必赘述。三个横向的旋律声部都不是线性截段，但中提琴与大提琴声部的纵向面等量于线性截段8-Z15，而小提琴主旋律声部则等量于8-Z15的补体4-Z15。于是，这段音乐和每个和声面都受制于基本集合的和声。

（三）重叠法的例子：

所谓“重叠法”，指的是两个或两个以上序列形式的重叠应用，每个序列形式用于织体中的一个声部或层次。

下例摘自勋伯格《管弦乐变奏曲》Op.31的主题，它表明勋伯格是怎样用基本集合去控制两个相重叠的序列形式（倒影关系的P与I₉）的和声结构的。

例7 勋伯格：《管弦乐变奏曲》Op.31

织体中的第一个片断是P的五音截段（1~5号音）和I₉的五音截段（1~5号音）的重叠；第二个片断是两个四音截段（6~9音）的重叠。最后一个片断理应是两个三音截段（10~12音）的重叠，但I₉的9号音“^♭B”的延长打破了这个规律。这段音乐的纵向和声结构是pcs“9-3”“8-9”和“7-4”，分别与基本集合的线性截段“3-3”“4-9”和“5-4”互补；如果第三片断的伴奏只包含I₉的10~12号音的话，它的纵向面便不能代表基本集合的和声，这就是^♭B音延长的意义所在。可见，勋伯格在他早期的十二音作品中，对和声结构的控制是十分严谨细致的。

下例表现得更为复杂，除两个移位关系的序列形式P与P₆相重叠之外，后半部中，P₆的材料又作“分割法”处理（与例5情况相似）：

例8 勋伯格：《钢琴组曲》Op.25

这段音乐包含有多种四音组的结合，为了便于叙述，我们将两个序列形式的四音组都用字母a、b、c来表示。

（1）模仿声部最初两音与上方声部重叠之后，构成一个与线性截段P_（a）等量的纵向和声结构pcs“4-12”。紧接着，P₆的3~4音与P的5~6音重叠，又构成另一个与线性截段等量的和声pcs“4-Z15”。

（2）在后一片断里，P_6（b）与P_6（c）相重叠，又产生局部的纵向和声pcs“4-18”与“4-5”（也与线性截段等量）；在节奏、音区等因素的作用下，这两个和声发挥着相对独立的作用。

（3）P_（c）与P_6（b）两个四音组的结合，产生一个不完全独立的纵向和声pcs“6-2”，正好等量于基本集合主要六音截段的结构。这个片断的完整的纵向和声PCS“9-10”又是线性集合“3-10”的补体。

（4）pcs“9-10”这个和声结构把P的最末一音“^♭B”排除在外。这样处理，一方面有节奏和句法作为依据，另一方面该音已转化成为下一个序列形式I₆的第一音，因而是合乎逻辑的。

以上各例表明，凡符合下列条件之一者，即可代表基本集合的和声：

1.本身就是基本集合的线性截段；

2.与线性截段等量；

3.为线性截段的补体。

以上的分析，使我们看到，勋伯格的十二音和声是严格服从于他的音乐空间的统一法则的。这个法则可用他的一句话来概括：“一首作品的和声已浓缩在基本集合中，基本集合又控制着整首作品的和声。”

四、集合的动机功能

前面曾经说过，基本集合具有主题的作用，但这种主题又不依赖于节奏、句法等外部特征。

基本集合中往往有一两个结构很有特点的音组。这种音组在作品中不断出现（当然也不依赖于节奏、句法等外部因素），起着类似“主导动机”的作用，从而加强了作品的结构力。这种集合的动机功能，早在勋伯格某些后期的自由无调性作品中已有明显的体现，显然是有意识的处理。

例9 勋伯格：《五首钢琴曲》Op.23 No.3

上例摘自勋伯格《五首钢琴曲》Op.23的第三首[9]。片断a是乐曲的开始，一个五音集合“^♭B、D、E、还原B、^♯C”以主题动机的姿态率先呈示在旋律中（其原型音级是“0，1，3，4，6”，音程涵量是〔223111〕，集合名称是“5-10”）；随后，该集合以不同音高和不同形态错综复杂地贯串在织体之中。如果把首次呈示的五音集合当作P的话，那么随后出现的那些等量集合便是它的T，TI和TRI（见上例d的图示）。片断b摘自临近结尾的第30~31小节，除一个类似持续音的五度音程（C-G）外，是两对由pcs“5-10”组成的倒影和弦在不同音区上的对置；这两对和弦同样起着动机的作用，与乐曲开始处的动机相呼应。片断c出现在该曲第14小节，在右手小三度音程作半音下行的和声背景下，四个结构为“5-10”的动机集合依次相交迭，十分巧妙地被组织成类似“分解和弦”的锯齿形音型。

再看看勋伯格第一部完整的十二音作品《钢琴组曲》Op.25中“嘉禾舞曲”的作法。在这首组曲的基本集合里，他设计了一个巴赫名字的动机pcs“4-l”（见下例图解），并在乐曲开始时以旋律形态得到加倍的呈示（见下例左手部分），到临近结尾的第26小节，这个动机的序数被打乱，变为“小九度与小二度交替”的半音阶片断，这似乎已面目全非，但它们仍然代表着巴赫名字的动机。

认识到集合的动机功能及其独特的表现方式之后，再去分析有关的十二音或无调性作品，就会发觉其中的逻辑性比原先所想象的要充分得多。

例10 勋伯格：《钢琴组曲》Op.25

例如桑桐的自由无调性作品《夜景》，其中第一主题的始末都由“半音下行然后再作三全音上行”这样一个三音动机构成（见下例a）；如用集合的观点去观察，便会发觉该曲后面出现一连串“纯四度十三全音”或“纯五度十三全音”的无调性三音和弦（见下例b）并不是偶然的，它们都是主导动机的另一表现方式，仅仅是把原先横向的旋律形态改变成为纵向的和弦形态而已，其作用不只是加强作品的无调性气氛，更重要的是主导动机的贯串。

例11 桑桐：《夜景》

注：“四度十三全音”与“五度十三全音”两种和弦的音级内涵分别为“0， 1，6”和“0，1，7”，但音程涵量相等，都是［100011］，实际上是倒影的关系。

下面请允许我引用鲁道夫·雷蒂《调性·无调性·泛调性》中的一个例子以及他的有关论点。

在无调性或泛调性音乐中，有时看来，作品似乎是没有主题的，雷蒂称之为“无主题音乐”。但雷蒂又说：“在音乐中，绝对无主题是一个不可想象的概念，因为它意味着对任何统一力的彻底排斥，最后连作曲家本人作为结构的组织者的作用也被否定了。”如果用“集合”的观点去观察，便会发现这种音乐实际上并非真正的“无主题”，只是放弃传统的主题手法而代之以集合的动机功能而已。

布列兹《钢琴奏鸣曲》第一号的例子正好说明这种动机功能：

例12

最初呈示的四音集合“^♯F，D，还原F，^♭E”被雷蒂称为“音响结构”（sound formation），实际上是“动机a”，随后出现的另一个四音集合“E，C，^♭E，^♯C”为“动机b”；它们交替出现，表现为“a b a b a”（中间插入少量非动机材料）。进一步观察，又可发现两个集合的原型音级，音程涵量以及名称都是一样的，分别为“0，1，3，4”，〔212100〕和pcs4-3 （12）。于是，这段音乐便同时兼有动机对比与动机贯串的性质，其统一力（或结构力）是显而易见的。（表格如下）

有一种叫“组合性”（combinatoriality）的基本集合，由两个结构相同的六音组，三个结构相同的四音组或四个结构相同的三音组构成。如把第一个音组当作原型（P），则其他音组便为它的移位或倒影移位。周晋民在钢琴五重奏《秧歌与山鼓》中所应用的就是这样一个组合性的基本集合（下例）：

例13

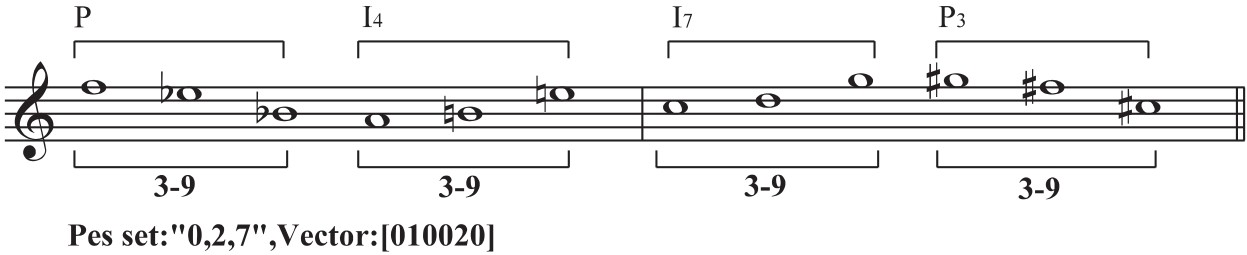
这个基本集合由四个结构相同（3-9）的三音集合组成，用这种基本集合作为材料，不论其织体作了多么复杂的变化，都可以认为，它是由一个单一的三音动机写成的。如果说十二音音乐的结构力表现为“被强化的主题一致性”（雷蒂语）的话，则用组合性基本集合创作音乐，便具有“被强化的主题一致性的再强化”这样一种加倍的结构力了。

五、尚待进一步完兽

然而，作为一种和声体系，只有强大的“结构力”是不够的，还必须具有能把音乐推向前进的“动力”。

调性和声以调性音阶为材料，十二音和声则以基本集合为材料；调性和弦由音阶每隔一音的要素组成，十二音“和弦”则由基本集合的线性截段组成；调性旋律具有明显的和声内涵，十二音旋律则本身就是和声。以上几个方面，都显示出在某种意义上十二音和声与调性和声的相似性。仅就“材料”对“和声”的控制而言，十二音和声的规律性与逻辑性的确是完全比得上调性和声的，甚至有过之而无不及。但另方面，调性和声的进行还受材料内部特有的调式功能所控制，而十二音和声的进行仅仅服从于基本集合有定序的音程关系。调式功能的逻辑可转化成为把音乐推向前进的力量（这种力量不必借助于其他外部因素），而音程关系的逻辑不具备这种相应的力量。简单地说，勋伯格用基本集合控制的十二音和声，虽有足够的“结构力”，却缺少类似调性功能的那种“动力”。虽然有定序的音程关系的逻辑在不断循环中会形成一种惯性，就像人造卫星被发射至轨道之后能绕着地球运转一样；如果基本集合在构成音乐过程中的这种惯性也算是一种“动力”的话，则这种动力还必须借助于力度、节奏、音区、音色等外部因素的配合才能有效地体现出来。难怪雷蒂认为“这种和声的唯一正当理由就是它对于音序的依附关系。”这话本身虽不含贬意，却道出了勋伯格十二音和声的美中不足。

既然美中不足，便有进一步完善的必要。

另一位对现代音乐研究颇有建树的理论家布林德尔在他的《序列写作》一书中，根据欣德米特关于和声紧张度起伏的原理，提出一套很有说服力和行之有效的处理十二音和声的原则。紧张度起伏的原理体现为“紧张—松弛”的矛盾统一运动，与功能和声中“不稳定—稳定”的矛盾统一运动相类似，无疑是非功能和声尤其是无调性和声产生“动力”的源泉。但与勋伯格的十二音和声相比，布林德尔的方法似乎太自由了，“偏离”和“变化”太多了，如果把两者结合起来，取长补短，让结构力与动力融为一体，岂不是一种更为完美的十二音和声概念和方法吗？这只是一种设想，至于如何结合，如何融为一体，便不是本文所讨论的范围了。

我在《十二音技法在中国音乐作品中的运用》[10]一文结束时曾提出过，“和声问题仍然是个薄弱环节，在某些作品中可以看出，作者在和声处理上还没有取得主动权。”本文目的，除了介绍勋伯格正宗的十二音和声之外，更重要的是为了引起同行的兴趣和关心，大家一起来探索十二音和声问题，使我们的十二音创作“更上一层楼”。

附件：阿伦·福特的集合表

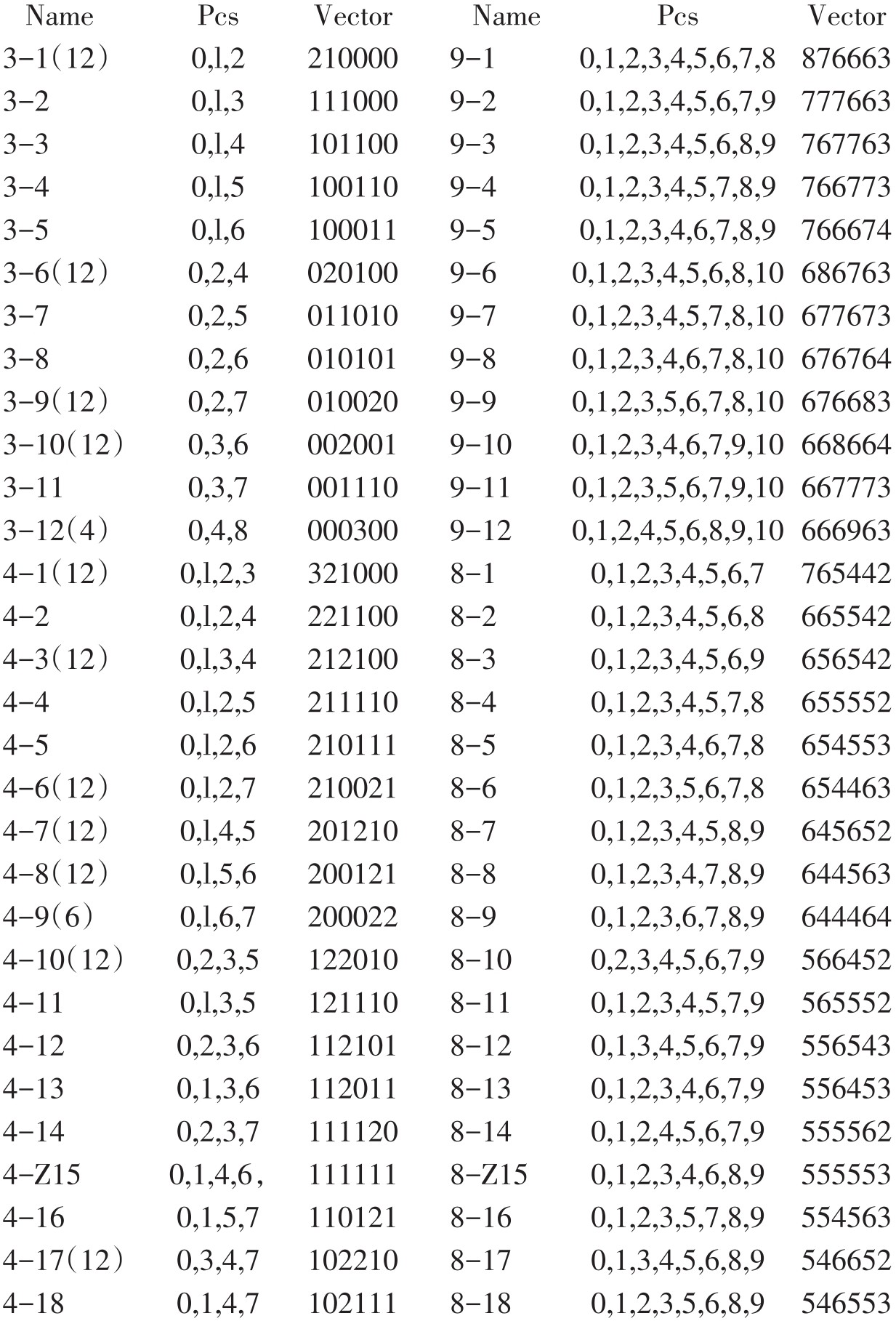
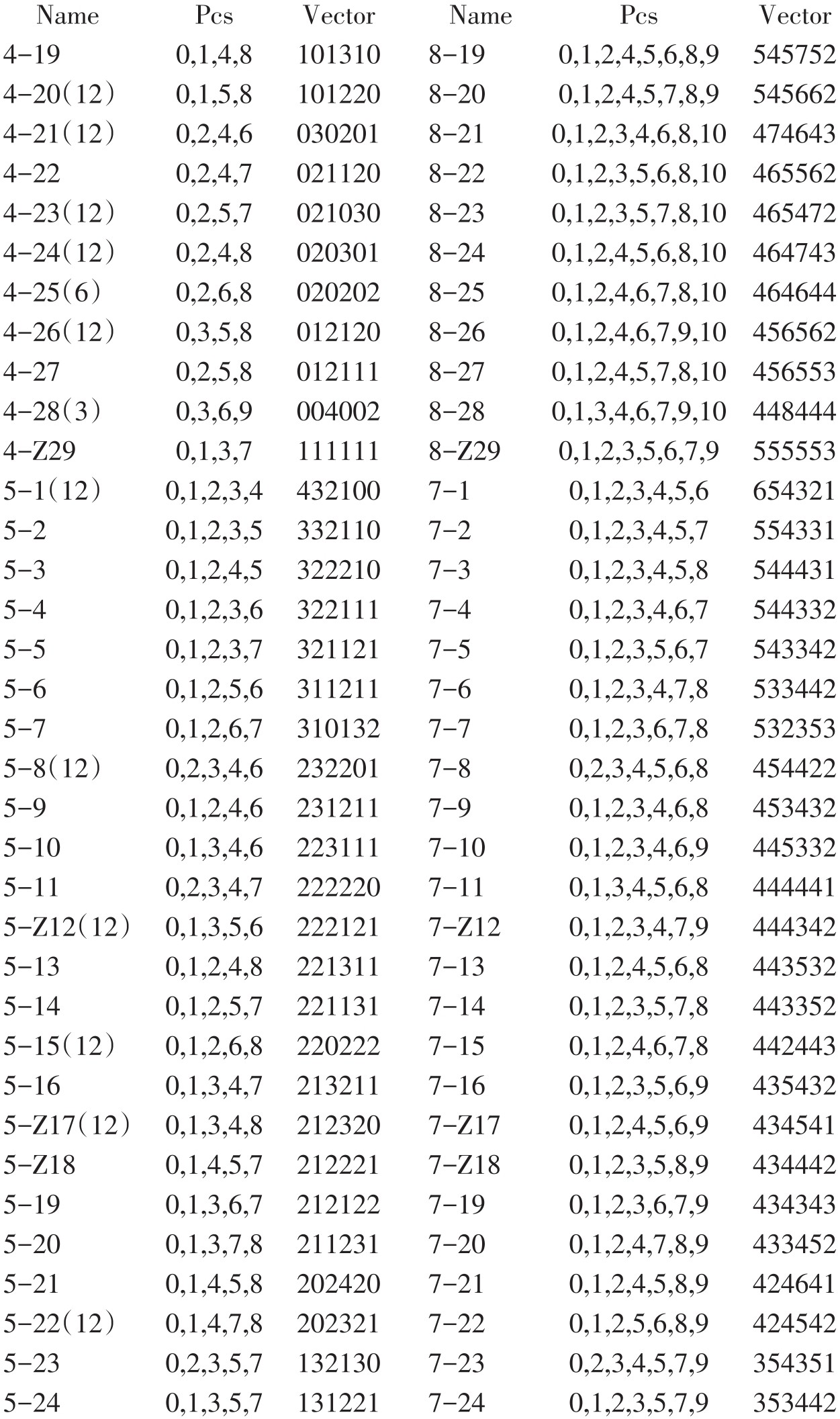
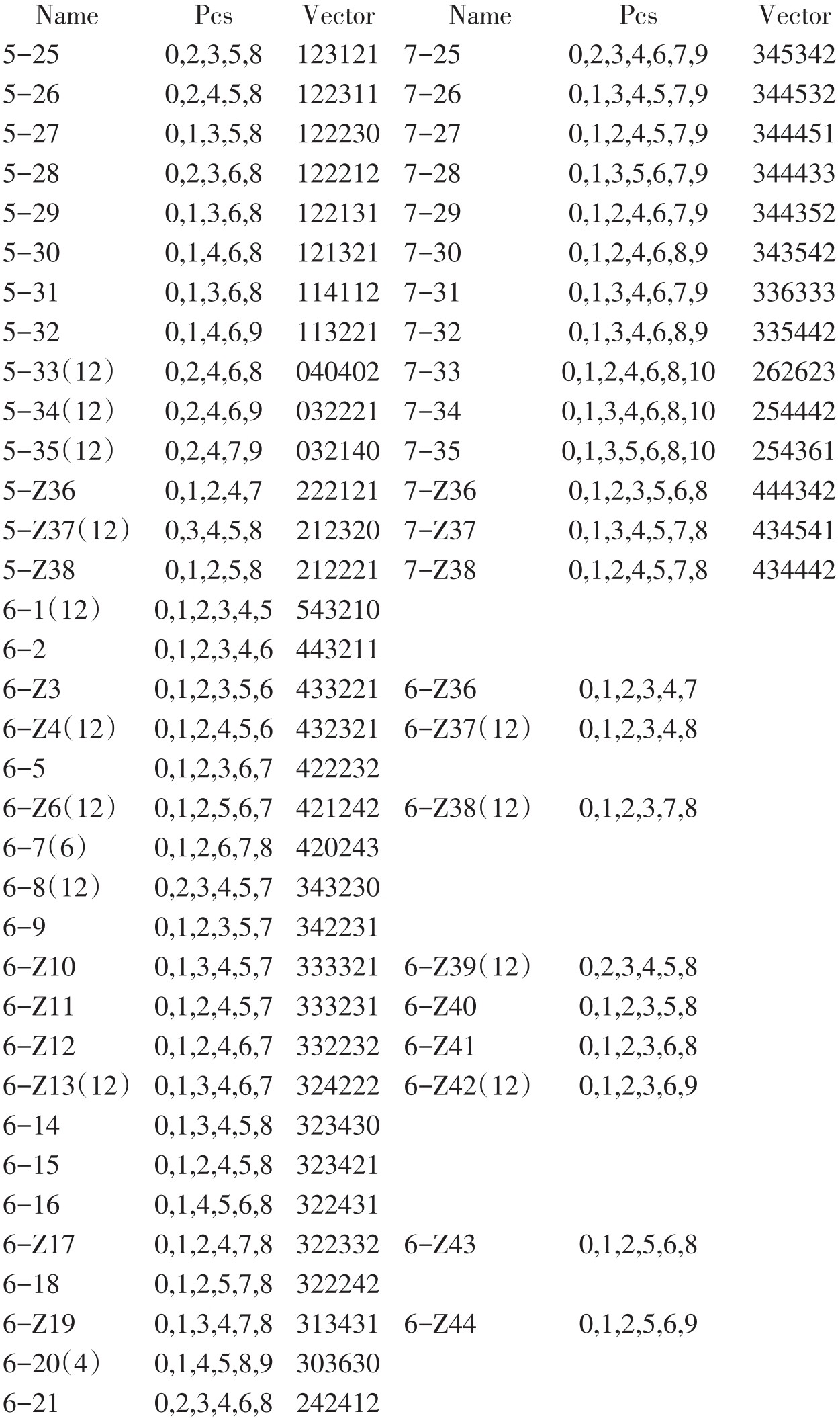
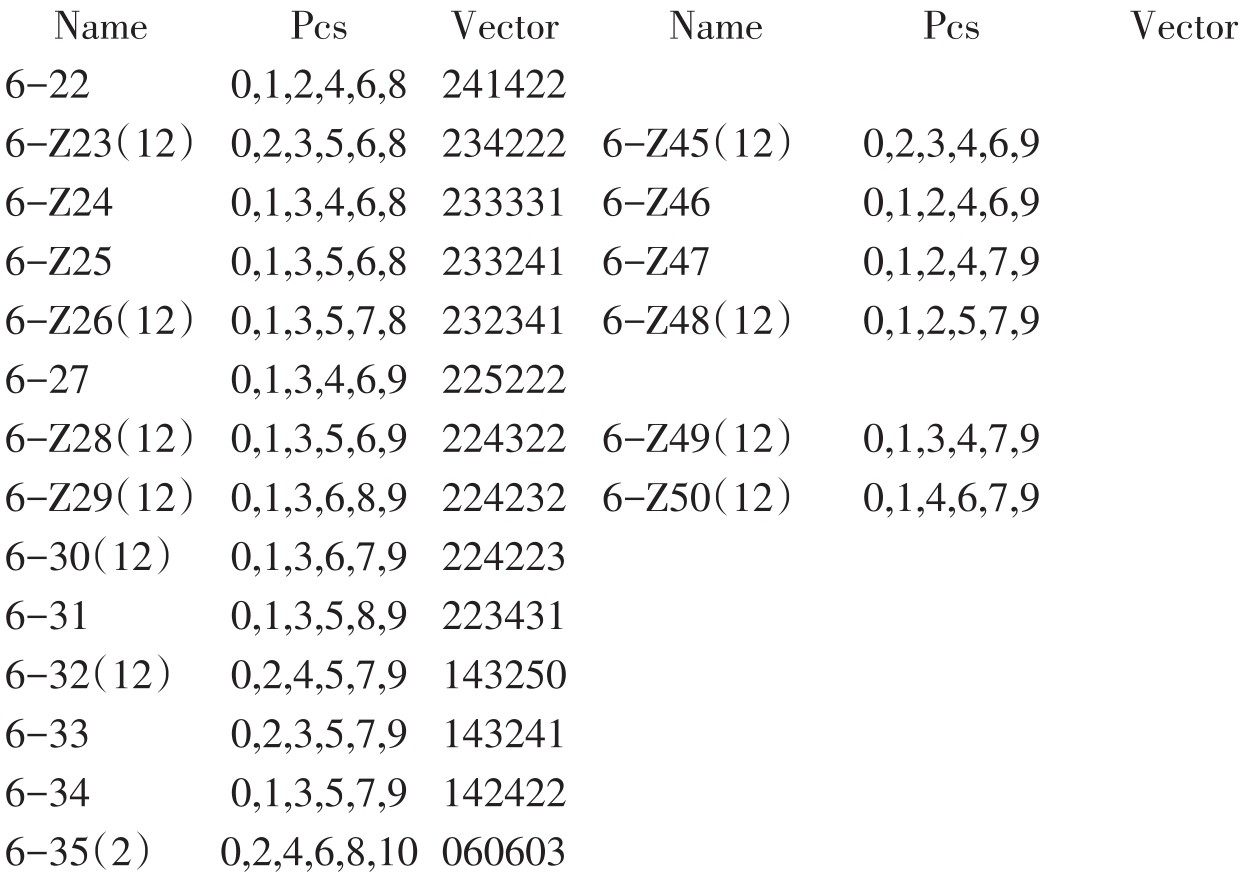
注　释

[1].摘自《用十二音作曲》一文的结束语。《用十二音作曲》（Composition With Twelve Tone）为勋伯格1941年3月在美国洛杉矶加州大学演讲的讲稿，后被伦纳德·斯坦收入他编辑的勋伯格文集《风格与创意》（Style and Idea）中，初版于1950年（纽约哲学图书馆）新版于1984年（加州大学出版社）。该书已出茅于润先生译本（上海音乐出版社2012年）。

[2].“基本集合”（bassic set）与“音列”（tonerow）“序列”（series）等词同义，详见本文第二部分。

[3].着重点为笔者所加。

[4].“线性截段”（Linear segment）简称“截段”，指基本集合中由序数连贯的音级构成的截段，有时也称“线性集合”或笼统地称为“音级集合”。

[5].勋伯格在讨论十二音写作时，一般不提“旋律与和声”，而是提“旋律与伴奏”，所谓伴奏，包括纵向形态的和弦，伴奏音型和对位声部。

[6].最好将“无调性音乐”理解为“非调性音乐”或“非调性思维的音乐”。

[7].以下例子都是勋伯格在《用十二音作曲》中引用过的，参照海德《勋伯格的十二音和声》中的分析方法。

[8].以上两点都是勋伯格在《用十二音作曲》中提出过的。

[9].该曲作于1923年2月，在《钢琴组曲》Op.25第一曲（十二音作品）之后。

[10].见《音乐研究》1986年第1期。