非调性音乐的结构(上篇·缩简版)
十一、非调性音乐的结构(缩简版)
改写说明
美国著名音乐理论家阿伦·福特(Allen Forte)1973年出版的《非调性音乐的结构》(The Structure of Atonal Music),借用数学“集合论”的基本原理来定量分析(解释)非调性音乐的结构,为新音乐研究作出了卓越的贡献。1986年我得到这本书(1977年第2版),由我当时的研究生杨衡展君将其译为中文,限于条件,只能出数量不多的油印本,但在国内业界有一定影响。今年(2008)中国音乐学院罗忠镕教授又译了一遍并交出版社出版。鉴于原书涉及数学方面的问题颇多,以致一般学音乐者读起来有一定的困难,故此,20年前我曾将该译本的上篇改写为“缩简版”,比阅读原版译文更加易懂。现因教学需要,我又将其中的上篇重新整理一遍,成为这个版本,希望对读者阅读原译本会有所帮助。
上篇:音级集合及其关系
一、音级集合
在非调性音乐里,音高组合体已不宜称为“和弦”,即使其组合形态与传统和弦毫无二致,其意义和用法也完全不同。我们将所有音高组合体都称之为“音级集合”(Pitch class set),简称“集合”(set)。应用“音级集合”的概念去对任何两个音高组合体进行比较,显得既简单又准确。
例1 勋伯格《乔治之歌》Op.15(第1首歌的结尾)

例2 韦伯恩《六首管弦乐小品》Op.6/3(第3首小品的开始)

例3

例3显示,把例1、2的各音记在最小的音域里,可发现它们原来是相同的集合,后者是前者的移位。它们是“等值”关系。
测度一个集合,为方便起见,应以以下原理为前提:
1.八度相等;
2.同音异名相等(不考虑音区)。
结果只有12个音级,用0,1,2,3……11等十二个整数来表示,取代通用的字母(音名)标记。这叫“整数标记法”(integer notation)。
例4

为叙述方便,以下我们将“音级集合”简称为“pc集合”,记在方括号内,如[0,1,2]。
二、集合的标准序及原型
在讨论两个集合之间的关系时,必须考虑到它们的顺序,因此有必要将一个集合化为“标准序”。集合的一次排序叫一个“换置”(per⁃mutation),换置的数量取决于该集合所含元素的数量。元素的数量称为“基数”(cardinal number)。基数通常用字母n来代表。一个含有n个元素的集合,便有1×2×3……n个不同的置换。例如三元素的集合,共有1×2×3=6个换置。这个运算用“n!”(即n的乘阶)来表示。
但,确定一个集合的标准序,不必考虑其所有的置换,只需考虑它的“循环置换”(circular permutation)即可。但有一个先决条件,即该集合必须以上行数字的顺序开始,而且每一个循环置换也必须保持上行数字的顺序。例如:集合[a,b,c]的第一个循环置换为[b,c, a],第二个循环置换为[c,a,b]。n个元素的集合便有n个循环置换。
当第一元素变成最末一个元素时,必须加以整数12,因12=0,其算术值不变。例如对集合[1,3,0]标准序的确定:

条件之一:标准序必须是首末两数之差为最小的置换。以上集合的标准序为A0。
条件之二:如有两个以上置换的首末整数之差相等的话,则选择第一位数与第二位数之差为最小值的置换。如两数仍相同,则选择第一位数与第三位数之差为最小值的置换。以此类推,直到二者的第一位整数与倒数第二位整数被检查完毕为止。如差数每次均相同,则任选一种作为标准序。
例如:

根据条件之一,A0与A3都可作为标准序;而根据条件之二,则A0才是最佳标准序。(A0与A3为反行关系)。
一个集合按标准序排序,且第一位整数被化为0,便被称为“原型”(或“基本型”)(prime form)。
三、移位相等的pc集合
例5 韦伯恩《五乐章的弦乐四重奏》Op.5/5

以上两个集合出现在同一作品的不同部位(第12小节和第25小节),表现形态也不同(前者为旋律,后者为和弦)。它们已按标准序排列,故可进行比较。
A:[2,3,7,8,9]
B:[0,1,5,6,7]
如果用i来代表pc整数,其移位就是i加某一整数t,结果产生pc整数j。如j大于或等于12,则用j除以12所得的余数来代替。这叫做“以12为模的加法”(略为“mod 12”)。
如集合A=B的话,必定有一个分别同A中每一整数相加之后可产生与B中每一整数形成一一相等的整数t。上例中的t为10,称为“移位算子”(transposition operator)。

例6 贝尔格《单簧管与钢琴小品四首》Op.5(1913)

上例A是该作品第一首开始处单簧管的音型,B是第三首开始处钢琴的音型。A移位等于B(移位算子t=4),或B移位等于A(移位算子t=8)。
移位算子对于非调性音乐来说显得特别重要,表面上很不相同的结构,可以在更基本的结构层次上是等值的。
四、反演相等的pc集合
注:“反演”是数学术语,相当于音乐中的“反行”或“倒影”,也叫“补数”(Complement),是集合论中“补运算”(Complementation)的专用词。为适应音乐学习者的习惯,下文论述中,有时会用“反行”来代替“反演”。
在移位相等的关系中,A的每一元素均与B的一个元素相对应,这种对应关系在任何情况下都具有唯一性,即A的某一元素不能同时对应于B的两个元素。用数学术语来描述这一程序,叫做“根据T法则,A映射上B”。
运用“映射”的概念,是传统音乐术语所无法达到的一种既方便又准确的手段。此概念的用处,在论述反行程序时尤为明显。
反行程序也按对应法则进行。这种法则将集合A的每一元素映射上集合B的一个元素。反行映射用I来表示,它是一种固定对应(fixed correspondence)。如:
I
0←→0
1←→11
2←→10
3←→9
4←→8
5←→7
6←→6
任何时候,双箭头所连接的两个整数之和都是12。映射I把集合A的每一元素映上其反行,从而产生一个新的相等的集合B。例如:A为[0,1,2],其反行为[0,11,10]
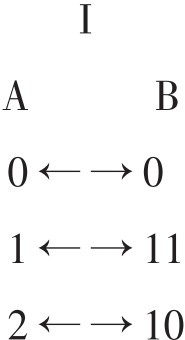
除移位相等外,两个pc集合如果能通过反行后接着进行移位而简化成相同的原型的话,二者即相等。用双映射(double mapping)来表示:
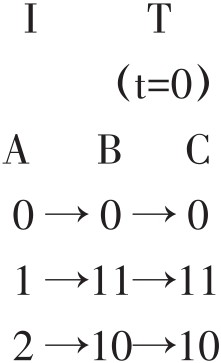
例7 勋伯格《乔治之歌》Op.15/6

注:根据其映射,证明B源于A。
将两个反行相等的pc集合进行比较时,必须颠倒后者的顺序。移位算子则等于每一对相对应的元素的和。
A:[3,4,7,10]
B:[8,7,4,1]
和:11 11 11 11
在继续讨论之前,先介绍一种表达移位和反行的符号标记(表达式),它对两个pc集合A与B进行简明描述是有用的。

前例两个集合A,B可写作B=T(I(A),11),意即“B是A的反演并在高度11上的移位”。
例8 艾夫斯《没有回答的问题》

这是艾夫斯早期的作品(1906),写作日期早于勋伯格的第一首无调性作品。第一片段包含第一个“问题”的最初两个音,在弦乐伴奏下由小号奏出;第二片段是第二个“问题”的相应音乐。两个片段的小号声部相同,伴奏不同,但A=D,B=C。我们根据的是映射和双映射公式:
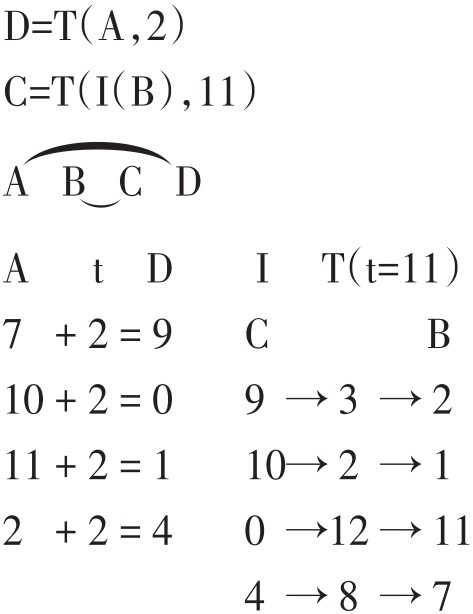
再例如:
例9 勋伯格《五首管弦乐小品》OP.16/1

五、集合原型及名称一览表
为了避免繁琐的描述而能快捷地查阅一个pc集合,有必要给集合的原型赋予一定的名称。名称由两端的数字和中间的连字号“—”组成。连字号左边是集合的基数,右边是集合的序号,即该原型在表中的位置。例如,“5-31”是下例中两个pc集合的名称,是集合表中基数为5(由5元素组成)的第31个集合(见附录的《音级集合表》)。
例10 贝尔格《奥尔腾伯格之歌》Op.4/2

斯特拉文斯基《木管乐器的交响乐》

要在集合表中查阅一个pc集合的名称,可按以下程序进行:
1.将该集合变为标准序;
2.进行移位,使第一位整数为0。
以上面二例为例:

已知两者为同一个集合,但在集合表中查不到[0,2,3,6,9],可见这不是最佳的标准序。因此,须求出该集合反行的标准序,并移至高度为0。
原标准序:[0,2,3,6,9]
反 行:[0,10,9,6,3]
上行排列:[0,3,6,9,10]
新的标准序:[9,10,0,3,6]
移位至0开始:[0,1,3,6,9]表中名称为“5-31”
这说明以上贝、斯二氏例子的集合是相等的,而且其原始形态只是原型“5-31”的反演。
六、pc集合的音程及其向量
为了对pc集合的性质以及集合之间的关系进行更全面的研究,还应对其音程向量进行讨论。
例11 贝尔格《沃采克》Op.7


A,C,D为旋律陈述,旋律音程即顺序各不相同。B,E,F为纵向陈述,音高级也各不相同。但因为总的“音程向量”是一个集合的更本质的特征,我们可发现,以上分布在该作品五个不同部位的,表现方式也不同的集合竟是相等的。
与12个音级(pc)相对应的,是12个音程级(interval class,简称ic),但经过转位,可简化为六个。
0=0
1=11
2=10
3=9
4=8
5=7
6=6 (省去0级,共有6个音程级)
如果要使一个整数的含义更加明确,必须在整数前标以pc或ic,尤其是在单独使用一个整数而为了避免误会时。音程级的概念,可使对一个集合总的音程内涵的描述简明化。以上例A为例:

注:10-11时,10应+12,即22-11=11=1;也可以倒过来相减,即11-10=1。
Pc集合总的音程内涵叫“音程向量”(interval vector,简称vec⁃tor)。音程向量的统计方法是:先统计ic1出现的次数,写下该数;再统计ic2出现的次数,写在前一位数的右边。以此类推,直至写完ic6出现的次数。结果,例11那个集合的向量为[102111]。
如果已知一个集合的“名称”或“原型”,则不必计算而可在表中直接查到它的“向量”。
七、音程向量的某些特征
在实际创作中,某些集合可能比其他集合起着更加重要的作用。原因是多方面的,但主要是这些集合的向量具有特殊的结构特征:
(1)唯一的向量项:
在所有220个pc集合中,只有4个pc集合其向量的每一项都是唯一的。
6-1 [543210]
6-32 [143250]
7-1 [654321]
7-35 [254361]
例如,pc集合“7-35”的原型是[0,1,3,5,6,8,10],正好与大调音阶相吻合。
例12 布索尼《第二小奏鸣曲》

上例第二小节第二拍上七个同时鸣响的音构成了pc集合“7-35”。但这些集合往往是以不同于调性音乐的方式出现的。
Pc集合“6-1”与“7-1”是我们熟悉的半音阶结构,其标准序分别为“0,1,2,3,4,5”和“0,1,2,3,4,5,6”。而“6-32”的排序正好与大调音阶的前六音相吻合:“0,2,4,5,7,9”
下面是艾夫斯《音之路》中“6-32”的纵向描述,出现在该作品的开头处。这种结构通常被称为“四度结构”,但在非调性音乐中,这名称是不恰当的。
例13 艾夫斯《音之路》No.1

(2)某ic的最大数:
上述四个具有唯一向量项的集合,还有另外的特征,即每个集合都包含有某一音程级的最大数。6-1与7-1以ic1为其最大数;6-32与7-35则以ic5为最大数。此外,还有另50个集合具有这一特征,这些集合,许多在非调性作品中占有重要地位。如:
例14 贝尔格《沃采克》Op.7

上例是pc集合“4-19”,“0,1,4,8”,[101310]。是包含ic4最大数的两个四元素集合之一(另一个是“4-24”),贝尔格以它作为“沃采克”的一个著名动机。在整部歌剧中,ic4在结构上的重要性是明显的,另一个事实也可作为证明:即结束每幕的和声都是“8-24”,它是包含ic4最大数的两个8元素集合之一(另一个是“8-19”)。
例15 贝尔格《沃采克》Op.7

[1,2,3,5,6,7,9,11]=标准序[0,1,2,4,5,6,8,10]
以ic6为最大数的pc set共27个,其中以“4-9”出现得最多。
例16 韦伯恩《五首管弦乐小品》OP.10/3

在上例中,这个集合出现在该乐章最初的旋律动机中。线性(横向)的陈述突出该集合中的两个ic6。
(3)向量项相等或近似相等的分布:
只有一种向量具有这一条件,即[111111]。至于“近似相等的分布”,是指4个以上的项是相等的向量,一共有29个。如:
例17 勋伯格《五首钢琴小品》Op.23/4

这里ic4三个音程紧接出现(见上例[ ]内)。
八、基数与音程内涵
本节要考察的是向量的某些更为抽象的结构特征(与基数有关)。
集合的基数决定其音程数。换句话说,基数相同的集合,其音程数是固定的。如:一个pc集合的基数为2,其音程数必定为1;如再加上一个元素,让基数增至3,这个新元素又可构成2个新的音程(每个新音程都包含有原集合中的一个元素)。
音程数随着基数的增加而增加,可用下表来表明:

一般情况下,如果pc集合的基数为k,音程数为n。求n的公式为:
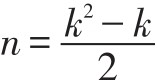
例如pc集合“5-7”,音程向量[310132],共10个音程。用上面的公式:
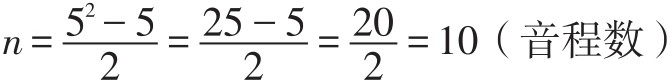
基数与音程内涵之间的关系具有更重要的意义。
1.一个pc集合的音程向量如果要表示出所有6种音程级,其基数至少应为4,而这样的集合也只有两个:4-Z15和4-Z29,即[111111]。
2.任何一个七元素以上的集合的向量都无“0”项。
3.任何一个五元素集合都至少包含有一个ic4。这意味着,只有当五元素集合所出现的ic4多于一个时,才要求分析时加以注意。
4.五元素与六元素集合的向量,“0”项最多只有三个。这样的集合只有两个:5-33和6-35。(这两个pc集合均为全音阶结构)。
含有一个或两个“0”项的五、六元素集合显得特别重要,这种集合涉及“不变性”(invariance),将在第12章讨论。
5.奇数(odd)音程级(ic1,3,5)在数量上多于偶数(even)音程级。在所有基数3至9的pc集合中,只有31个集合的音程分布是偶数多于奇数的。其中大多数(18个)属于奇数为5和7的集合。这些基数的集合比其他基数的集合更难“驾驭”。见下表:
奇—偶数音程分布状态
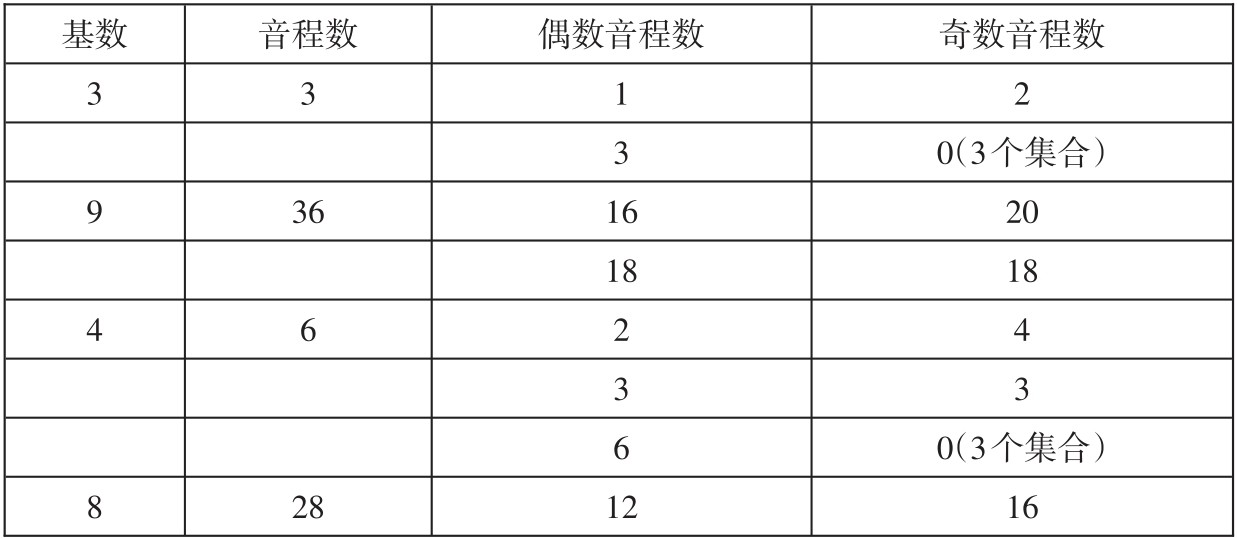
续表
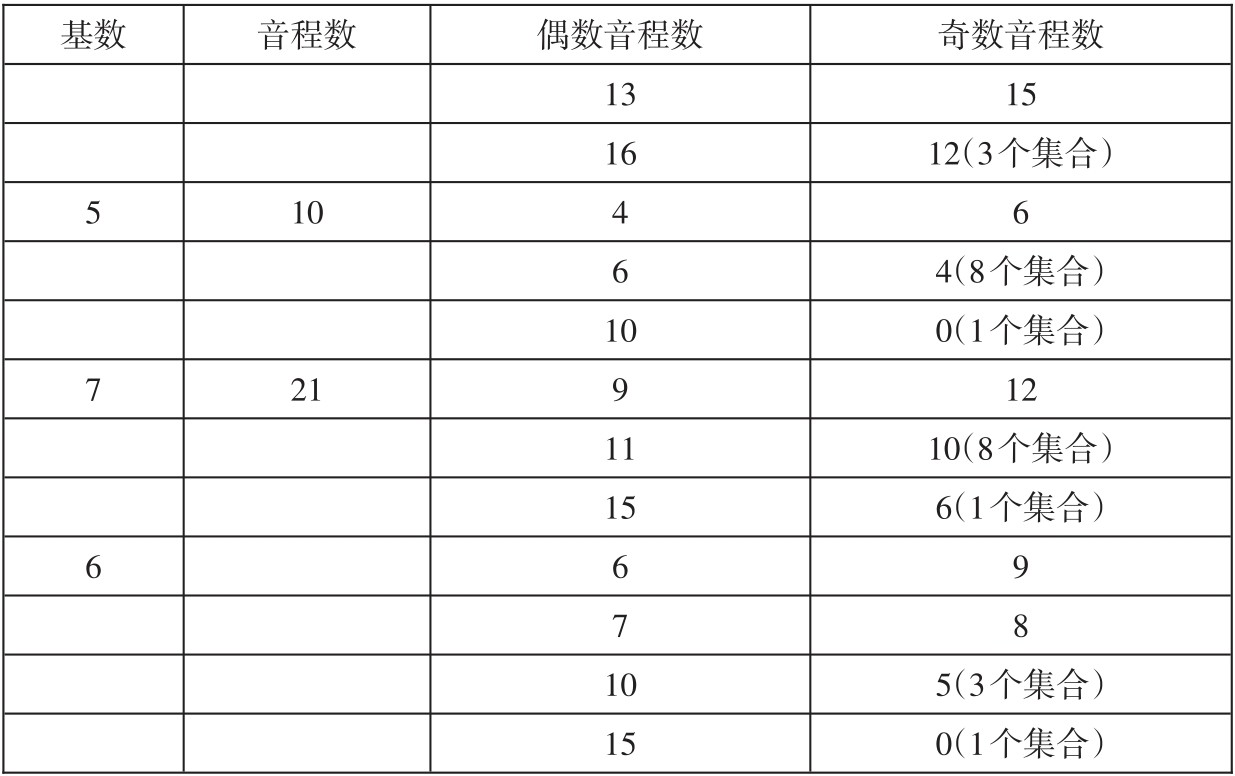
从上表可看出,基数为9的集合,根本不存在偶数音程多于奇数音程的情况。
九、向量相同而不相等的pc集合
在一般情况下,两个pc集合通过移位或反演移位之后,可化为相同的基本型者,这两个集合便可认为是相等的。由此推论,似乎每个基本型的音程向量都是唯一的。但事实并非完全如此。例如,全音程四音集合4-Z15和4-29,它们的音程向量同为[111111],却不能通过移位或反演移位化成同一个基本型。这两个pc集合便称为“Z关系对”(Z-related pair)。这种关系对共有19个,如5-Z12与5-Z36;6-Z10与6-Z39……等。(四音集合有1对,五音集合3对,六音集合15对)。
现在又出现了一个分析上的问题:既然二者具有相同的向量,能否简单地选择其中的一个作为原型,而把另一个看作是它的“变体”?不能!除非以基本的pc集合结构作为区别的基础,而把相同的向量看作是“从属因素”,否则便不能在“音高级结构”与“音程级结构”之间找出其必然的和有说服力的区别。但是,以音程内涵为基础而把Z关系的集合视为不相等,其最大的理由是由音乐数据所提供的。这一点也是本书所最关注的。
在非调性作品中有大量例子,说明pc集合起着最重要的作用。
例18 韦伯恩《三首短曲》Op.11/1

A 6-Z10:[2,4,5,6,8,9]=[0,2,3,4,6,7]
B 4-Z29:[0,1,3.7]
C 6-Z10:[4,5,7,8,0,11]=[0,1,3,4,5,7]
D 2-1:[10,11]
E 4-Z15:[1,2,5,6]
注:①A与C为反演关系。
②B+D=6-Z39,与6-Z10为Z关系对[333323],6-Z39是B与D的并集(union)。
③B与E也是Z关系对[111111]。
上例几个Z关系集合在作品中是紧相连接的。再看另一个例子(下例),两个片段相隔很远,6-Z37是第二小提琴开始的横向旋律;而6-Z4是乐章结尾四种乐器的总和。它们的音程向量都是[432321]。
例19 韦伯恩《6首小曲》Op.9/4

Z关系集合(尤其是六元素的)还有其他特性,以后还将谈到。
十、pc集合的子集
例20 贝尔格《沃采克》Op.7

以上第一个例子摘自该歌剧的开始处,其中第二个集合(最后一个纵向和弦)是5-30。
第二个例子是“我们穷人”(Wir arme leut)的动机(曾在例14中引用过),与主人公密切联系并贯穿整部歌剧的始终,是集合4-19。
第三个例子是另一动机,是集合5-30,与歌剧开始处的集合相同,其中包含作为最后四个音的4-19。
最后一个例子是“我们穷人”动机的扩展(加上一个音)。构成集合5-30。
以上说明,4-19包含在5-30之中,即4-19是5-30的“子集”。换句话说,5-30是4-19的“母集”(Superset)。
通常,当集合B的每个元素都是集合A的元素时,B便为A的子集,记作B⊂A(读作“B是A的子集”)或A⊃B(读作“A是B的母集”)。
那么,一个集合包含有多少个子集呢?现以三元素集合[0,1,2]为例:
1元素子集有3个:[0]
[1]
[2]
2元素子集有3个:[0,1]
[0,2]
[1,2]
3元素子集有1个:[0,1,2]
0元素子集有1个:[Φ](称为“空集”,empty set)
以上这个三元素的子集数为8。
说明:
①子集是无序的,[0,1]与[1,0]相同。
②空集是任何集合的子集。
一般情况下,一个n元素的集合有2n个子集,例如上面那个3元素集合有23=8个子集。但其中有的子集在理论上和分析上是没有意义的,必须尽量简化。这就涉及“真子集”的概念。
只有当X⊂Y,并且X≠Φ,X≠Y时,X才为Y的真子集。
如上面那个三元素的集合,[Φ][0,1,2]的子集是无意义的;而且,单元素子集也是无意义的(上面的[0],[1],[2])。于是,子集的数量应为2n-(n+2)。(注:n为单元素子集数,2为“x=y”数+空集数。任何集合都有这么两个无意义的子集,应排除在外。)
尽管将“无用”的子集排除掉,作最大限度的简化,随着基数的增大,子集的数量也迅速地增大。

对上表的解释:23-(3+2)=8-5=3
24-(4+2)=16-6=10
25-(5+2)=32-7=25
那么,一个基数为n的集合,包含有多少个基数为m(m≠0,m≠1, m≠n)的子集呢?下面的公式可求出这个数字:

注:“!”为“乘阶”。
以下附表(帕斯卡三角形,Pascal’s triangle)为我们提供了基数为n的集合中基数为m的子集的数量。n值写在左边“行”里,m值写在上方“斜行”里。
例如:一个基数为4的集合,其中基数为2的子集共6个;基数为3的子集共4个。
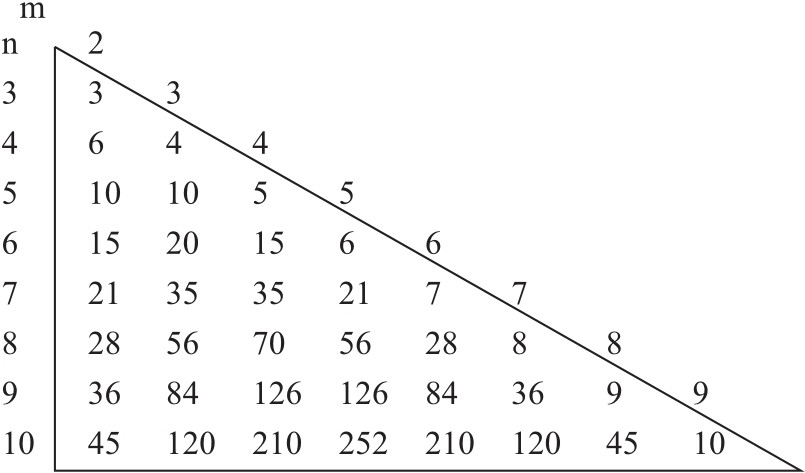
上表所提供的数字是准确的,但对于分析和结构理论的引申却没有多少用处。因为,例如一个10元素集合有210个4元素子集,但真正性质不同的4元素集合(即基本型)总共也只有29个。可见,有许多是重复的(被多重表达的)。
因此,对一个集合来说,我们不仅应知道它含有多少个某种基数的子集,还应知道它包含有什么样的子集(子集的名称)。
例21 韦伯恩《五乐章的弦乐四重奏》Op.5/4

这是一个“子集饱和”(Subset saturation)的例子,四音旋律“4-9”的四个三元素子集均可简化为相同的基本型“3-5”[0,1,6]。
以下是子集分析的更大规模示范:
其中的8元素集合“8-24”是例15引用过的(摘自《沃采克》,该集合出现在歌剧每幕的结尾处,贝尔格称之为“准终止和弦”)。“8-24”中包含有许多动机式的,在歌剧中起主导地位的集合,如4-19,5-30 (均见例20)和6-34。
例22

4-19,5-30,6-34三个集合在8-24中被展示过四次(8-24以标准序出现,下面四个排列成行的都是6-34;而符杆朝上的是4-19,朝下的是5-30。皮尔将这个8-24称为“整部作品中最重要的参考和弦)。
下例是《沃采克》中两次用6-34作旋律(横向)陈述的例证:
例23 贝尔格《沃采克》Op.7

在分析中,往往涉及到用子集来描述集合问题。下例30那个五元素集合(5-32),摘自贝尔格Op.2/3,但三个例子用三种不同的描述方法。
例24

注:此例包括原书的例30、31、32,以下的描述仍称其为例30、31和32。
我们把例30的五音集合A看成有B,C,D三个子集。B是B音上的小三和弦,C是B音上的大三和弦,D是B音上的小七度;整个“5-32”被描述为:在B音基础上同时混合着大、小三和弦而产生的四音和弦“B-D-♯D-♯F”,加上七音A。也可看成是一个“属七和弦”和一个“小七和弦”的综合。把“5-32”看作是两个传统三和弦和一个单元素子集的结合的描述法,显然是受传统概念所支配的,因为没有理由把这些子集看作比其他子集更重要,更具特点。
例31,32提供了同样可行的描述。例31的子集也是三和弦,却把单元素子集排除开(实即包含进B中);例32用不同类型的子集,并且都不是三和弦,显然更接近非调性的观念了。
当然还有另外的描述法,关键是,应善于选择用来描述一个集合的特殊的子集。这又涉及到“不变性”(invariance)的概念。
十一、移位中的不变子集
已知相等的集合A与B,第三个集合C为A与B中的元素所限定,这个集合便称为A与B的“交集”(intersection),并记为C=·(A,B)。这样一个集合的元素称为“不变音级”(invariant pitch-class),或简称“不变式”(invariants)。
例25 斯特拉文斯基《三首弦乐四重奏小品》之2

上例可以说明非调性音乐中“不变式”的作用。在A,B对(都是4-8)重复6次之后,出现了一个由集合[4,9]组成的对比片段(第4小节),接下去又是开始对A,B的再陈述。A与B是集合“4-8”的移位相等形式,二者的关系为:
B=T(A,11)
应用于4-8的这个T值精确地限定了两个不变式,形成子集[4, 9]。这个不变子集,在第1小节的初次陈述与第6小节的再次陈述之间提供了一种直接的结构连续性。
不变性的概念与发展、变化、连续、非连续等直观的音乐概念有着密切的联系,要了解非调性音乐的基础,离开这一概念是不可能的。下面让我们来对移位中的不变性作系统的考察。
音程级与移位算子之间有一种直接的对应关系,因此,任何移位t值所产生的不变式数量,可从向量项显示出来。例如pc集合3-1的基本型[0,1,2],它的音程可用一对表示为O1和O2的“运算域”(Oper⁃ands,代表某两个pc整数)之间的差数来表示。
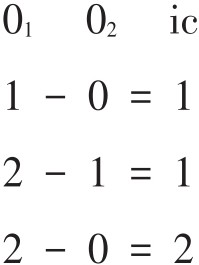
因为有2个一级音程和1个二级音程,故其音程向量为[210000]。当音程级(ic)数量转换成为移位算子(t)时,其结果为:
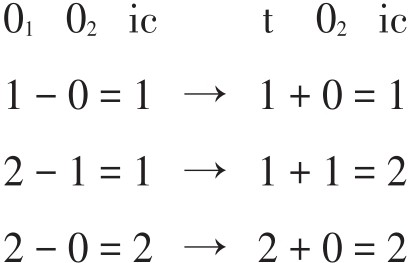
注:从ic转换为t用“→”为标记,而且后面要恢复到O1,故不用减法而用加法。
当t值为1时,不变式数量为2(pc1和pc2);当t值为2时,不变式数量为1(pc2)。这样,我们可从音程向量中直接判断出不变式的数量了。例如,ic1的项为2时,意味着在t=1的条件下进行移位时,该集合有2个元素不变;ic2的项为1,意味着在t=2的条件下移位,有一个不变式;ic3为0,意味着t=3时,不变式为0。余类推。
例如,5元素集合“5-30”,其vector为[121321],直接观察可得知:
t=1,不变式为1;
t=2,不变式为2;
t=3,不变式为1;
t=4,不变式为3;
t=5,不变式为2;
t=6,不变式为1。
“5-30”的基本型为[0,1,4,6,8],t=1的移位[1,2,5,7,9](不变式1个,即pc1,♯C)。余类推。
再以7-35(大音阶)vector[254361]为例,可用下面的图解来表明移位与不变式数量的关系:(谱表上下方配成对的移位算子是反行的关系,实际上最多为6;当t=6时,产生了两个不变式,而ic6的向量项则是1。这说明反演关系的t值总是产生相同的不变式数量,而ic6的向量项必须“×2”才是t=6时不变式的正确数量。

关于移位的不变式,有三种特别重要的情况:
1.极大值不变性;2.极小值不变性;3.包含两个以上集合及反演关系的t值的不变性。
例26 贝尔格《单簧管与钢琴小品四首》Op.5/1

此例说明“极大值不变式”。
例26a,b是该作品第一首和第三首开始处的旋律形态,它们都是6-Z44,B=T(A,4)。6-Z44的向量是[313431],t=4的移位可产生4个不变式[0,4,7,8](基本型为[0,1,4,8])。例26c是它的移位。这种不变子集具有作品结构成分的意义。此例c中4-19的出现已说明这一点。同一作品中另外几个重要的集合也包含有4-19。
例27(下例)是7-21[10,11,2,3,5,6,7],出现在该作品第三首的一个重要的结构部位上,例26c那个4-19[11,3,6,7]作为7-21的子集,反复出现达7次之多,而7-21中再没有另一个四元素的集合出现过3次以上。
例27 贝尔格《单簧管与钢琴小品四首》Op.5/3

下例说明“极小值不变式”。
例28 斯特拉文斯基《春之祭》

大管旋律以t=11的移位在[12]处反复。6-32(以上集合)是具有唯一向量项的集合([143250]);于是,11是准确地被限制在一个固定不变的pc上的唯一的t值,这个pc便是11(B)。结果,第一次陈述中作为装饰性旋律音的B,在第二次陈述中成为主要旋律音♭C。
此外,括号内那个四音音型(pc set3-7)已包括在6-32的移位形式中,并成为紧接出现的“春天的预兆”段落中突出的特征,达到从“引子”到下一段落之间的连接目的。
例29 勋伯格《乔治之歌》Op.15/1

此例包含四个“4-2”集合(A,B,C,D),但不太容易看出+(A,B)与+(C,D)是移位相等的。+(C,D)=T(+(A,B),8),名称为6-2,向量[443211],不变子集为[2,4]。两个段落的联系是这样安排的:1.第二段落中用不变子集中的pc4开始了第一个四音子集(C);2.而pc6和8本只属于第一段落,但被用来作为第二段落的伴奏,因而加强了两个6音集合的联系。
例30 斯特拉文斯基《春之祭》

此例揭示了在一个小小片段内等值集合的本质。
B=T(A,11),有趣的是:不变子集[2,5,9]以附点二分音符持续着,而其他元素是变换的(中间一行谱)。音程内涵保持不变的同时,有一种音级内涵的变换起伏。
例31 勋伯格《五首钢琴小品》Op.23/2


A:[3,4,6,7,8,9,10,11,0]“9-3”的基本型[0,1,2,3,4,5,6,8,9]
B:[11,0,2,3,4,5,6,7,8] 向量:[767763]
C:[7,8,10,11,0,1,2,3,4]
D:[5,6,8,9,10,11,0,1,2]“7-21”的基本型[0,1,2,4,5,8,9]
E:[9,10,0,1,2,3,4,5,6] 向量:[424641]
F:[1,2,4,5,6,7,8,9,10]
(将以上A,B,C,D,E,F的9音集合与“9-3”相对照;将下面划线的与7音集合“7-21”相对照。)
前面已提过,反演关系的t值(如8与4,7与5)产生相同数量的不变式;反演关系的t值在移位条件下也产生相等的不变子集。
Pc集合9-3的三种不同形式各呈现在上例的每一小节中。第18小节为A,B,C;第19小节为D,E,F,其移位关系可图解如下:
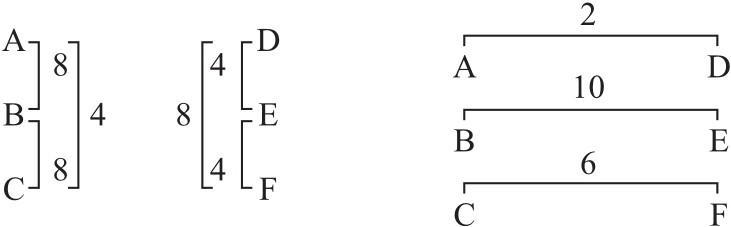
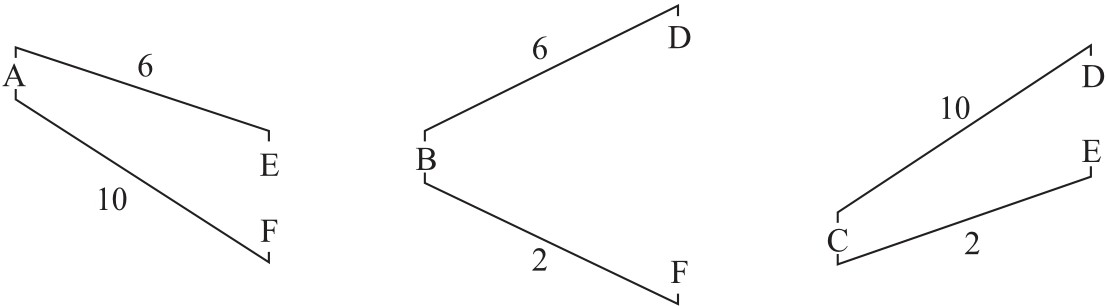
注:以上分别为纵向关系,横向关系和斜向关系。
Pc集合7-21是第18小节三对集合和第19小节三对集合每对之间的不变子集。2和10的t值包含有pc集合6-2的不变式;6的t值则包含有pc集合6-30的不变式。
基数为n的集合中拥有基数为n-1的不变子集一览表(略)
只有29个集合具有这种性能,其不变关系可从左向右读,重复的情况(如8-24与8-21共同拥有7-33不变式)除外。
8-1拥有7-1不变式,但8-1在移位中并不拥有3-1不变式。这个链条并不是连续的。
虽然在移位中只有五个8元素的pc集合拥有7元素子集不变式,但8元素集合通常固定地拥有大量的五元素与六元素集合。只有8-28是例外。
十二、反演中的不变子集
孤立来看,移位中不变式的数量是不受一个集合的特定音级所限制的,而只受该集合的音程内涵所限定。但在反演移位中,pc集合便成为决定因素了,因而更趋复杂化。
例32 勋伯格《月迷彼埃罗》Op.21

5-31 [114112]
这是《月迷彼埃罗》中一首间奏曲第一段的结尾。在这一曲式的交接点上,两个纵向集合A,B有着共同的名称“5-31”。它们之间唯一的非不变式是pc1和pc2(见上例)。按第五节所述,B是A的移位反演(t=3):

※比较两个反演相等的集合,须将后一集合颠倒过来(以上B已颠倒)。
※A,B的不变子集是[0,3,6,9],因为5-31的向量[114112],t=3时有4个不变式。
再举一个类似的例子:
例33 鲁格尔斯《天使》

以上集合是“5-21”,[202420]。A是B的t+0的移位。C的出现则包含着反演移位的关系。
B:[10,11,2,3,6]
C:[11,10,7,6,3]=T(I(B),9)有4个不变式。
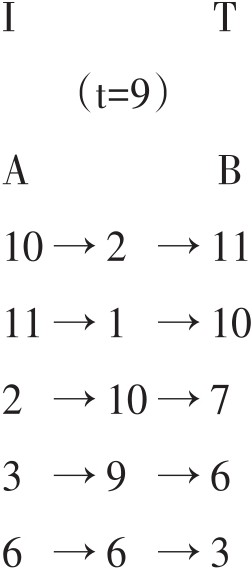
注:反演移位与单纯移位,其不变式不相等。
以上二例,仅移位也可产生4个不变式;那么,是否反演的结构效应与仅通过移位所产生的结果完全一样呢?不是的!
下面讨论“反演移位”中不变性的结构原理(再次使用映射标记):
以集合S:[0,1,2,3](“4-1”,[321000])为例。其双映射为:
S T(I(S),0) T(I(S),1)
0 → 0→1
1 → 11 → 0
2 → 10 → 11
3 → 9→ 10
S的任何元素用a来表示;S反演的任何元素用a1来表示;移位的结果用x来表示。
双映射首先把a传送到a1上,再传送到某元素x上。
a→a1→x
因为反演关系已构成固定的“对”(fixed pairs),所以,可变的t值便成为双映射中最基本的因素。那么t值是什么呢?我们可用以下的演绎来说明。t=x+a。
(1)根据a+a1=0 mod 12(反演定义)
(2)a1+t=x(移位定义)
在不改变其值的条件下,后一表达式可通过在等式两端同加a而得以改变:
(3)a+a1+t=x+a
因为a+a1=0,故可得出:
(4)t=x+a
例34 斯特拉文斯基《春之祭》

S:“8-28”,[0,1,3,4,6,7,9,10][448444]
A:“7-31”,[4,6,7,9,10,0,1][336333]
原型[0,1,3,4,6,7,9]
B:“7-31”,[1,3,4,6,7,9,10]
C:“7-31”,[10,11,1,2,4,5,7]
D:“7-31”,[7,8,10,11,1,2,4]
E:“7-31”,[11,1,2,4,5,7,8]
※号处为不变子集6-27[1,4,6,7,9,10]
原型[0,1,3,4,6,9]
S是8元素集合“8-28”,以变化多端的前后关系贯串出现在整个作品中。其特征之一是,八个七元素子集均为“7-31”,上例是它的五次出现A,B,C,D,E。
集合B是A的t=9的移位,※号处的6元素集合是A与B的不变式。7-31的向量为[336333],显然,这种t值的移位可产生6个不变式(即※处的6-27)。整个小节都是8-28(通过7元素的子集)派生出来的。Pc集合7-31在第2小节(C)重新出现,实际上完全由持续的二分音符表现出来。
C与B的比较表明:C=T(I(B),8),并产生四个不变式。在单纯的移位中,没有任何一种t值刚好可以产生四个不变式的(这里,不变式子集为4-28,是8-28的补集),可见“反演”是具有特殊意义的。
上例最后一小节,D是C以“t=9”(这也是B与A移位的t值)的移位。其最大不变性产生的6-27[10,11,1,2,4,7]仍然是它们之间的不变子集。最后,E=T(I(D),9),仍然保持最大的不变性。但这个不变子集6-Z13,尽管它在作品其他地方是重要的结构成分,但在这里并无特殊意义。
十三、相似性关系
上面几节论述了集合的相等关系,即一对相等关系的集合可通过移位或反演移位而简化成相同的基本型;在此意义上,两个集合是相等的。本节要讨论的是相同基数而不相等的集合之间的相似性,如何测定二者之间的相似性程度。
例35 艾夫斯《没有回答的问题》

以上两个片段5-10和5-Z12具有共同的四元素子集4-13[10,1, 3,4],这叫“音级相似性”(pitch-class similarity)。
我们可给两个基数n的集合S1和S2,以及基数为n-1的集合S3的相似性关系Rp下定义:
Rp(S1,S2)当且仅当。(S3⊂S1,S3⊂S2)
简言之,S1和S2必须包含有一个基数为n-1的共同子集,二者才呈Rp关系。
这似乎是测定两个集合相似性关系直截了当的方法,但其弊病是显而易见的。例如,例35中那个5-Z12与38个五元素集合中的18个呈Rp关系;5-10则与22个五元素集合呈Rp关系。这样的Rp关系实际上没有什么特殊意义。但如考虑两个集合之间音程级的相似性,则具有更重要的意义。
仍以例35的两个集合为例:
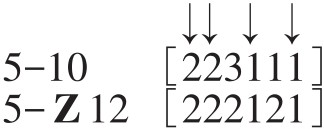
它们之间的ic1,ic2,ic4,ic6四个向量项是一致的。拥有四对这种对应关系的向量项的一致性,称为“极大相似”(maximally similar);因为任何两个向量中,对应一致的向量项最多是四对。
以音程向量来测定,极大相似性包含两种关系:R1和R2。R2已如上述,而R1的两个向量必须具有相同的数字,除四个向量项是相对应的之外,还有两个是互换的:

相对来说,R1比R2的关系更为密切。例36便是两个R1关系的集合。
例36 威伯恩《六首管弦乐小品》Op.6/1

第一行谱是5-9:[4,7,3,5,9]=[3,4,5,7,9]=[0,1,2,4,6] (原型)
第二、三行5-24:[5,1,3,6,11]=[11,1,3,5,6]=[6,5,3,1,11]=[0,1,3,5,7](原型)
5-9:[231211]
5-24:[131221]
这是例36中两个集合的向量,观察其中每个向量项,可发现与上面“4-2”和“4-3”的关系完全一样。
与“极大相似”相反的是“极小相似”。两个向量如果没有对应一致的向量项,便为“极小相似”(minimally similar),标记为“R0”,如例勋伯格的《幸运之手》Op.18中的两个集合:
4-2 [3,4,5,7] [221100]
4-13[8,11,1,2][112011](谱例略)
各种相似性程度可概括如下:
Rp音高级的极大相似性
R0音程级的极小相似性
R1音程级的极大相似性(有互换位置的特征)
R2音程级的极大相似性(无互换位置的特征)
如果把Rp和ic相似性(R1与R2)结合起来考虑,相似集合的数量还会大为减少,甚至出现意料不到的特殊关系。
(原书)例51的两个三角矩阵,说明基数为4的集合的单纯Rp关系和复合关系“。(R1,Rp)”的区别:
(图略)
左图:以集合“4-2”为例,在标2的行中从左向右读,读到尽头再向下读,可得知:4-2与4-1,4-3,4-4等呈Rp关系(共19对)。
右图:用同样方法读,4-2只与两个集合4-3,4-22呈复合关系。
上图说明,在基数为4的246对呈Rp关系的集合中,只有22对兼有Rp和R1关系。
(原书)例52表明,基数为4的集合,有66对同时兼有Rp和R1或R2的关系“(Rp,+(R1,R2)”。
同时兼有音级和音程级的极大相似性,被认为比单纯的音级相似性或音程级相似性更为重要。
同时兼有R0和Rp关系的集合对“(R0,Rp)”,数量非常少。(原书)例53表明此情况。
各种相似性关系的矩阵详见原书“附录2”。
还有一种情况:两个集合在音程上为极大的相似关系,而音级则是极小的相似关系,我们用“-”来表示逻辑否定(“非”),记为:(+(R1, R2),-Rp)。(原书)例54的矩阵表示基数为5的集合的这种关系。
例37 贝尔格《沃采克》Op.7

5-Z17[0,1,3,4,8]
5-19[11,0,3,5,6]=[0,1,3,6,7],二者的音级不是极大相似。但查阅(原书)例54的矩阵,证明5-Z17与5-19为(+(R1,R2),-Rp)关系。
十四、顺序关系
在非调性音乐里,无序集合是一种更基本的概念,顺序关系也不像移位或反演一样被普遍地应用于置换之中。但顺序关系有时也显得十分重要。
例38是一个简单的顺序的例子。
例38 斯特拉文斯基《巴尔蒙特的两首诗》(之一)

B是A的重新排序。结果,B中的两个pc(9和0)保持原来位置,而另两个pc(5和11)的位置被颠倒过来。
请注意:有序集的表示方式与无序集的表示方式有区别。有序集的数字之间相隔一定的距离,以区别于用括号表示的无序集。
在非调性音乐中,把pc集合的置换视为移位或反演移位后的重新排列,是非常重要的。例38中的B可视为A按t=0移位后的重新排列。
例39 韦伯恩《大提琴奏鸣曲》(1914)

例39表明更复杂的重新排序。
A:5 2 63
B是A(t=9)的移位;
(t=9) 21130
C是B(t=3)的移位;
重排 B:0 11 3 2
D是C(t=5)的移位。
(t=3) 3 2 6 5
重排 C:3 5 6 2
(t=5) 8 10 11 7
重排 D:11 10 8 7
结果是:C与A的pc内涵相同,因而可对二者进行比较,以测定位置重新排列的数量。我们看到,C中只有pc6的位置保持不变。
既然所有集合都是移位关系,就有理由对任何一对集合的顺序关系进行比较,就像对A和C进行比较一样。
A以t=9进行移位而产生“2 11 3 0”,这叫“有序移位”(ordered transposition)。将A的“有序移位”与B进行比较,体现了一种特殊的重新排列:两个元素保持不变,另两个元素互换位置。
例40 韦伯恩《六首管弦乐小品》Op.6/3

A:15011
(t=8)B:9187
例41 韦伯恩《五乐章的弦乐四重奏》Op.5/5

A:3 9872
(t=8)B:11 5 4 3 10
以上都是有序移位的例子。
再来看“有序反演(移位)”。
同“有序移位”相比,“有序反演”的概念更加复杂,它涉及双映射。
在“有序反演(移位)”中,起作用的主要是“音程连续”(interval succession),即相邻的pc所构成的音程连续。
例42 勋伯格《乔治之歌》Op.15/2

音程连续被用连字号隔开,记在方括号内的数字来表示。但还有一种更简明的表示法,叫“基本音程型”(basic interval pattern),缩写为bip。
例43 勋伯格《五首管弦乐小品》Op.16/2

可用上例来说明bip的概念。
该片段包含pc集合5-4的三种形式。下面列出的是它们的有序pc集合,音程连续和基本音程型。
bip
A:8 4325 [4-1-1-3] 1134
B:101987 [3-4-1-1] 1134
C:0 311109[3-4-1-1] 1134
基本音程型是音程连续的标准化,其标记的数字按上行顺序组合,数字间不用连字号。这种简化形态告诉我们,所有三种形式A,B, C,其总体连续音程是相同的。
例44是pc集合6-Z13的两种形式,但其总体连续音程内涵(bip)却是相异的。
例44 韦伯恩《六首歌曲》Op.14/1

上例A,B的bip中。仅有一个共同的位数。两个片段的对比还发音法、音区、节奏和音色等其他方面。
根据重新排序的音级去直接比较一个集合的两种形式是行不通的。
音的重新排列,可能影响也可能不影响音程的连续,在顺序反演与bip之间,便没有简单的对应。
十五、pc集合的补集
十二个音级的集合(即整数为12的集合)构成“全集”(universal set)用“∪”表示。
从∪中选出一个n元素集合,可有效地将∪划分成两个集合,即n元素集合和12-n元素集合。或者,设M表示被选出的一个4元素集合,N表示余下的一个8元素集合,那么,就∪来说,M为N的“补集”(complement);反之,N为M的“补集”,其关系记为:
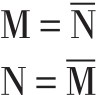
在非调性音乐中,补关系起着最基本的结构作用。
例45 韦伯恩《四首歌曲》Op.12/4

A:[3,7,8,9] (4-5)
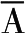 =+(B,C) (8-5)
=+(B,C) (8-5)
B:[10,0,2,4](4-21)
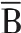 =+(A,C) (8-21)
=+(A,C) (8-21)
C:[11,1,5,6](4-16)
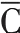 =+(A,B) (8-16)
=+(A,B) (8-16)
注:此片段由全部12个pc组成。
上例∪被划分为A,B,C三个集合,任何一个集合的补集均由其他两个集合的并集构成。
从“集合基本型一览表”的排列中可以查阅到:4-5的补集是8-5, 4-21的补集是8-21,等等。基数为6的集合属于例外,后面单独进行论述。
例46是一首作品中两个相隔很远的部位的补关系,比例45更加复杂。
例46 勋伯格《五首钢琴曲》Op.23/3

第一部分为该曲主题(用K表示),可简化为pc集合5-10。
第二部分为该曲的结束段落,出现了K的发展形式及其补集7-10。这一补关系由M、P两个镶嵌式结构组成。M可简化为pc集合7-10,其中含有子集N(5-10),音级与K相同。P也可简化为pc集合7-10,所含子集Q(5-10)则与K无共同音级,构成了极小不变性(仅有一种t值在反演移位中不产生不变式)。我们不仅承认从音级上看得出来的pc补集为补集,也承认任何补集的移位或反演移位。例46的t值确切表明两片段的相互关系。下面是这种关系的概括:

把一个集合与其补集进行比较时,使用较小基数更方便。例46中的pc集合7-10以两种方式表示:①按实际的pc内涵记在方括号内;②或根据其补集(字面上的)的pc内涵,转化成标准序,记在圆括号内。例46下方就是这样做的。
由此可见,要鉴别一个集合,没有必要涉及基数大于6的集合。例如要鉴别基数为9的集合,只要找出它不包含的3个pc,并确定其基本型,然后在“集合表”上查阅即可。
既然一个集合的补集可以是移位的或反演的,在不变式对应的意义上,一种更为基本的性质可以从音程向量中找到。
试比较5-35和7-35的向量:
5-35[032140]
7-25[254361]
除ic6的向量项之外,7-35中的每一个向量,都比5-35中相对应的向量项大2。这种固定的对应关系可以看作是音程级分布的比例规律。也就是说,补关系集合之间相对应的向量项的算术差,与该两集合的基数的差(d)是一致的;ic6的向量项属于例外,其中d必须除以2,因为6是其自身的反演。若给定一个集合S的向量,便可轻而易举地确定-S的向量来。
例如:已知4-Z15的向量是[111111],对其中从ic1到ic5的每个向量项都分别加以4,而对ic6则加以2,便是其补集8-Z15的向量:
4-Z15[111111]
8-Z15[555553]
鉴于这种音程比例,我们有理由把一个集合的补集视为该集合的一种简化(如8-Z15简化为4-Z15),或放大(如4-Z15放大为8-Z15)的重复形式。
一个集合的补集被包含在该集合之中,补集便为该集合的特殊的子集;或反之,该集合为补集的特殊的母集。
除7-Z12不包含子集5-Z12之外,每个大于6的集合至少有一次包含其补集。其极值如下:

例如:8-19:[0,1,2,4,5,6,8,,9]
4-19:[0,1,4,8]
8-19的8个补关系子集为:[0,1,4,8]
[1,2,5,9]
[1,5,8,9]
[4,5,8,0]
[5,6,9,1]
[5,9,0,1]
[8,9,0,4]
[9,1,4,5]
例47 斯特拉文斯基《三首弦乐四重奏》之三

此例是该作品的结尾。两个结束音♯G,E的出现,使这里包含有8-19的八种形式的补集(4-19);而如果没有这两音,那个纵向和弦6-22便只包含有一个4-19。补关系在某种程度上解释了前面其他地方(该乐章第7小节和第14小节)为什么用4-19作为结束和声。
六音集合的补关系比较特殊。在50个六元素pc集合中,有20个是自成互补的,如6-1的补集仍是6-1。然而Z关系六音集合的补集却是它的Z关系对应集,如6-Z3的补集是6-Z36,等等。
包含与不变性的概念,与补关系的概念相联系。根据这种联系,可作音程相似性关系测定的延伸。例如,对基数为7和基数为5的集合进行比较:
例48 斯克里亚宾《两首诗》Op.63/1

测定7-26与5-33的关系:
第一个集合为A,第二个集合为B,第三个集合为C。
B为A(t=3)的移位。前两个集合是相等的,但与第三个集合则差别很大。
(下略)
十六、截段取样
在进入下篇“集合复合型”之前,必须先掌握“截段取样”的分析过程。所谓截段取样,就是确定(判断)作品中哪些音乐单位可作为分析的对象。
我们把传统意义上的相对独立的结构单位称为“基本截段”(Pri⁃mary segment)。例如一个具有节奏特点的旋律音型(通常有休止符隔开或共同的横杆符尾)、纵向的和弦、固定音型,等等。
不断截段取样的程序称为“交叠”(imbrication),即对一个结构的组成部分作连续地提取。下例为线性交叠的例子:
例49 勋伯格“无词歌”(选自《小夜曲》)Op.24

注:以上a为“基本截段”,b为“交叠”。
“交叠”是确定一个基本截段中的附属截段(subsegment)的基本方法。同样重要的是一个以上的基本截段相互作用所构成的“复合截段”(composite segment)。所谓“复合截段”,是由一些截段或相邻的附属截段,或由某些其他方式相连的截段所构成的音乐单位。
例50可作为复合截段的最初实例。
例50 勋伯格《五首管弦乐小品》OP.16/1

整个旋律线构成集合6-5:[4,5,6,7,10,11]。
头两个旋律音与伴奏和弦构成“复合截段”6-5:[6,7,8,9,0,1],与上方声部单独构成的集合相等。
(上篇完)
