5.7 函数的递归
函数作为一种代码封装,可以被其他程序调用,当然也可以在函数本身内部代码中被调用,即自己调用自己。这种函数定义中调用函数自身的方式称为递归。
递归就像是一个人站在装满镜子的房间中,看到的影像就是递归的结果。
递归在数学和计算机应用上非常强大,能够非常简洁地解决重要问题。
在前面案例中我们定义了数学中求阶乘的函数,其实这是一个经典的递归例子。阶乘的定义如下:
![]()
在前面的函数定义中,我们使用一个简单的循环累乘来实现阶乘的计算。但是仔细观察这个公式,比如计算5!,可以变成5!=5×4!,如果去掉5,那就只需计算4!,依次类推,就会发现n!=n(n-1)!,这时可以有另一种表示阶乘的公式:
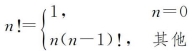
从这个定义中可以看出,0的阶乘是1,其他数的阶乘是这个数乘以比这个数字小1的数的阶乘。
递归的基本思想是将一个复杂的问题转换为若干个子问题,子问题的形式和结构与原问题相似,求出子问题的解之后根据递归关系就可以获得原问题的解。
递归有两个基本要素。
①基例:子问题的最小规模,用于确定递归何时终止,也称为递归的出口。
②链条:即递归模式,将复杂问题分解成子问题的基础结构,也称为递归体。
递归函数的一般形式为:

上例求阶乘不用循环,而改用递归来解决,就是每次递归都是计算比它更小数的阶乘,直到1!。1!是已知的值,称为递归的基例。递归的链条就是n!=n(n-1)!。依据递归函数的一般形式,可以写出求阶乘的代码:

fact()函数在定义时内部引用了自身,形成了递归过程,而无限制的递归将耗尽计算资源,因此必须设计基例,使得递归逐层返回。函数体中用到了if语句给出的n为1时的基例,一旦递归层到了n=1时,fact()不再递归,返回数值1。
递归过程如图5-6所示。
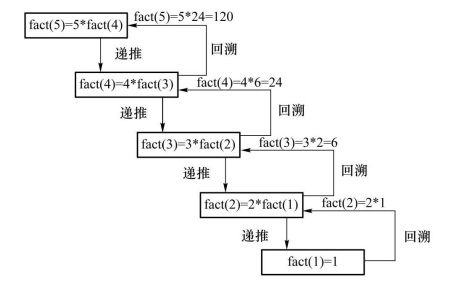
图5-6 递归过程
递归遵循函数的语义,每次调用都会引起新函数的开始,表示它有本地变量值的副本,包括函数的参数。每次调用时,函数参数的副本都会临时存储,递归中各函数再运算自己的参数,相互没有影响,当基例结束运算并返回值时,各函数逐层结束运算,向调用者返回计算的结果。
程序运行结果如下:

注意:使用递归,一定要注意基例的构建,否则递归无法返回,将会报错。
在数学中,有一个非常有名的数列(斐波那契数列),可以使用递归来实现。斐波那契数列的公式如下:
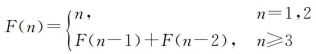
使用递归函数来实现,代码如下:


运行结果:

斐波那契数列是由数学家昂纳多·斐波那契以兔子的繁殖为例子而引入的,故也称为“兔子数列”。兔子的繁殖故事是这样的:一般兔子出生两个月后就有繁殖能力,一对兔子每个月能生出一对小兔子,如果所有的兔子不死,那么一年后有多少对兔子。兔子的繁殖示意图如图5-7所示。
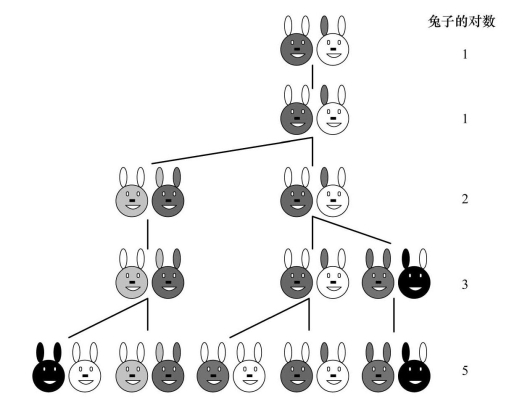
图5-7 兔子的繁殖示意图
兔子数量统计如表5-1所示。
表5-1 兔子数量统计

【案例5-6】 理财计划。
银行推出了一款理财计划“重复计息储蓄”。储户只需在每个月月初存入固定金额的现金,银行就会在每个月月底根据储户账户内的金额算出该月的利息并将利息存入用户账号。现在如果某人每月存入k元,请计算一下,n月后,他可以获得多少收益。
输入数据仅一行,包括两个整数k(100≤k≤10000)、n(1≤n≤48)和一个小数p(0.001≤p≤0.01),分别表示每月存入的金额、存款时长、存款利息。
案例分析:
根据题目要求,可以列出收益规律表,如表5-2所示。
表5-2 收益规律表

程序代码:

用递归实现:

【案例5-7】 汉诺塔。
有3个立柱A、B、C。A柱上有大小不等的圆盘n个,较大的圆盘在下,较小的圆盘在上。要求把A柱上的圆盘全部移到C柱上,遵循大圆盘在下、小圆盘在上的规律(可借助B柱)。每次移动只能把一个柱子最上面的圆盘移到另一个柱子的最上面。请输出移动过程。
案例分析:
这是动态规划问题中的一种。移动规则:
·规则一,每次移动一个圆盘。
·规则二,任何时候都是大圆盘在下面,小圆盘在上面。
实现方法:
(1)当n=1时
直接把A上的一个圆盘移动到C上,即A→C,如图5-8所示。
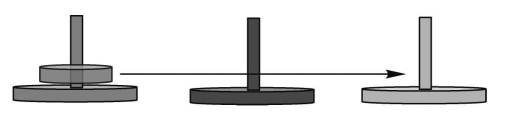
图5-8 一个圆盘的移动
(2)当n=2时
先把小圆盘从A放到B上,即A→B。再把大圆盘从A放到C上,即A→C。最后把小圆盘从B放到C上,即B→C,如图5-9所示。
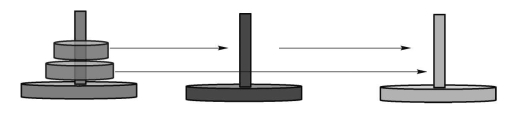
图5-9 两个圆盘的移动
(3)当n=3时
先把A上的两个圆盘,通过C移动到B上去,调用递归实现。再把A上剩下的一个最大圆盘移动到C上,A→C。最后把B上的两个圆盘借助A,挪到C上去,调用递归实现。
(4)当n=n时
先把A上的n-1个圆盘借助C,移动到B上去,调用递归实现。再把A上的最大圆盘,也是唯一一个,移动到C上,A→C,即递归出口的条件。最后把B上的n-1个圆盘借助A,移动到C上,调用递归实现。
在移动中得到递归出口的方法是:将最后的大圆盘从A移动到C。
递归的链条是:某柱上的n-1个圆盘借助另一个柱,移动到指定柱上去。
实现代码如下:

运行结果如下:

