5.8 迭代
从直观上讲,递归是指将大问题化为相同结构的小问题,从待求解的问题出发,一直分解到已知答案的最小问题为止,然后再逐级返回,从而得到大问题的解(就像一棵分类回归树tree,从root出发,先将root分解为另一个(root,sub-tree),就这样一直分解,直到遇到leaf后逐层返回),过程如图5-10所示。
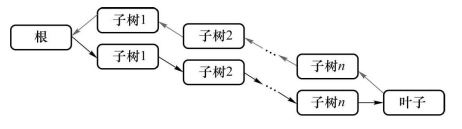
图5-10 递归过程
迭代则是从已知值出发,每次将前一步已知的赋值传递给后一步,可以循环地使用同一段代码来递推,不断更新变量值,一直到能够解决要求解的问题为止。迭代过程如图5-11所示。
![]()
图5-11 迭代过程
迭代与普通循环的区别是:循环代码中参与运算的变量同时是保存结果的变量,当前保存的结果作为下一次循环计算的初始值。
迭代难以理解但效率高,递归易于理解但效率低,死递归会造成栈溢出,内存开销大。
递归算法从思想上更加贴近人们处理问题的思路,而且所处的思想层级算是高层(神),而迭代则更加偏向底层(人),所以从执行效率上来讲,底层(迭代)往往比高层(递归)高,但高层(递归)却能提供更加抽象的服务,更加简洁。
使用迭代算法要解决3个方面的问题。
(1)迭代变量的确定
在可以用迭代算法解决的问题中,至少存在一个直接或间接不断由旧值递推出新值的变量,称为迭代变量。
(2)建立迭代关系式
迭代关系式是指从变量的前一个值推出其下一个值的公式(或关系)。
(3)对迭代过程进行控制
迭代过程的控制通常分为两种情况:一种是所需的迭代次数是个确定的值,可以计算出来,这时可以使用一个固定的循环来控制迭代过程;另一种是所需的迭代次数无法确定,这时应进一步分析结束迭代过程的条件。
迭代函数的一般形式为:

【案例5-8】 母牛的故事。
有一头母牛,它每年年初生一头小母牛。每头小母牛从第四个年头开始,每年年初也生一头小母牛。请编程计算在第n年的时候,共有多少头母牛?
案例分析:
参考兔子数量的算法,也列出一个表格,计算出每一年母牛的数量,然后在这些数字之间找出规律,如表5-3所示。
表5-3 母牛数量

·前4年没有小牛产子,每年数量与年数对应。
·第4年,对应有4头母牛,4=3+1。
·第5年,对应有6头母牛,6=4+2。
·第6年,对应有9头母牛,9=6+3。
由此可以看出数量是有规律可循的,该年母牛的数量就是一年前的数量再加上三年前的数量,用公式表示就是F[n]=F[n-1]+F[n-3]。
基例为前三年的母牛数量,F(1)=1,F(2)=2,F(3)=3。
链条为F[n]=F[n-1]+F[n-3]。
用递归函数实现:

![]()
运行结果:

改成迭代实现:

运行结果:
![]()
从两个程序的运行结果看,计算同样多的数量,递归需要占用更多的内存,执行的效率也低。数据量越大,差别越明显。
从程序的设计来看,递归就是不停地自己调用自己,从根一层一层往叶分解:return cow(m-1)+cow(m-3)。而迭代则使用交换赋值的形式,复用循环从叶一层一层往根传递值:f1,f2,f3=f2,f3,fn。
