2．1 数 制

虽然计算机能极快地进行运算，但其内部并不像人类在实际生活中使用的十进制，而是使用只包含0和1两个数值的二进制。 当然，人们输入计算机的十进制被转换成二进制进行计算，计算后的结果又由二进制转换成十进制，这都由操作系统自动完成，并不需要人们手工去做，学习计算机，就必须了解二进制（包括八进制／十六进制）。

数制就是用一组固定的数字和一套统一的规则来表示数的方法。

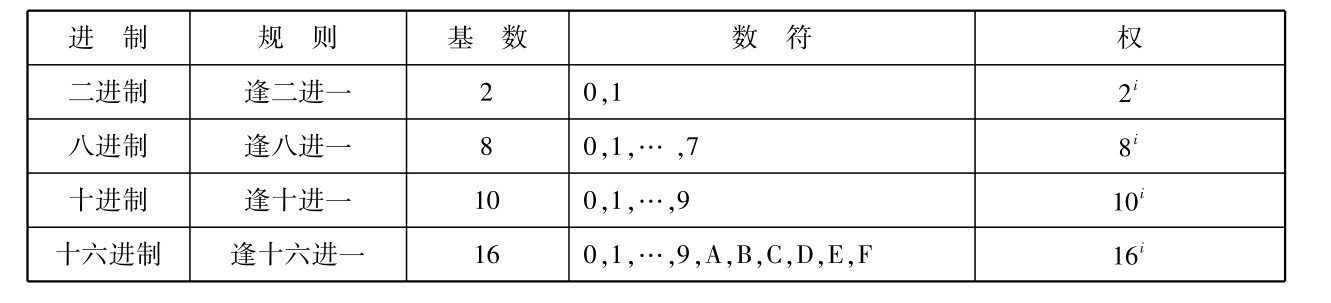
按照进位计数的数制成为进位计数制。 日常生活中采用的是十进位计数，而在计算机内处理信息采用的是二进位计数。 在进位计算的数字系统中，如果用R个基本符号（如0，1， 2，…，R－1）来表示数字，则称其为R进制，R称为该数制的基数，Ri称为权（i为整数，如3，2，1，0，－1，－2，…）。

进位计数的编码符合“逢R进位”的规则。 各位的权是以R为底的幂，一个数可以按照权位展开成多项式，例如，（123．456）10＝1×102＋2×101＋3×100＋4×10－1＋5×10－2＋6×10－3。

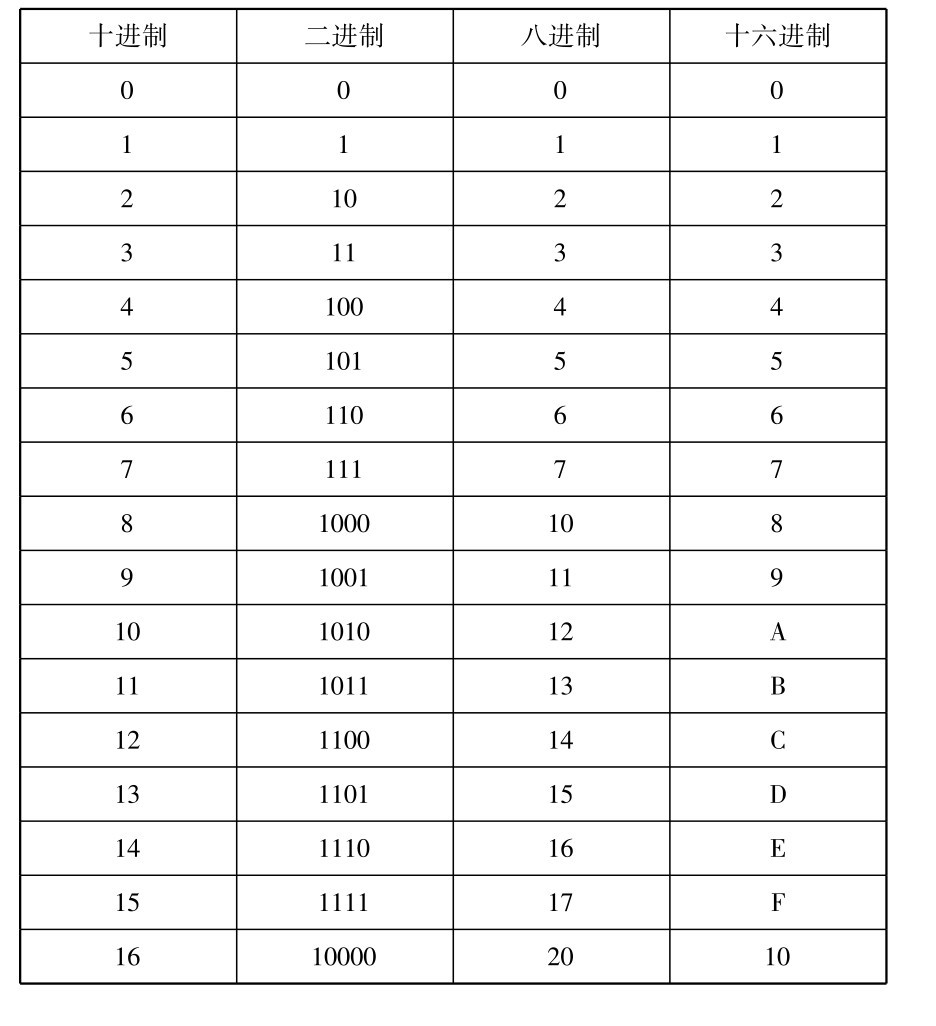
计算机中经常用到的进制有二进制、八进制、十进制和十六进制等，它们之间的特点对比见表2．1，数值对比见表2．2。

数制符号表示：二进制B（binary）；八进制O（octal）；十进制D（decimal）；十六进制H（hex⁃adecimal）。

表2．1 二进制、八进制、十进制和十六进制特点对比

表2．2 二进制、八进制、十进制和十六进制数值对比