2．2 数制之间的转换

2．2 数制之间的转换

2．2．1 十进制数转换成R进制数

要将十进制数转换为等值的二进制数、八进制数和十六进制数，需要对整数部分和小数部分分别进行转换。

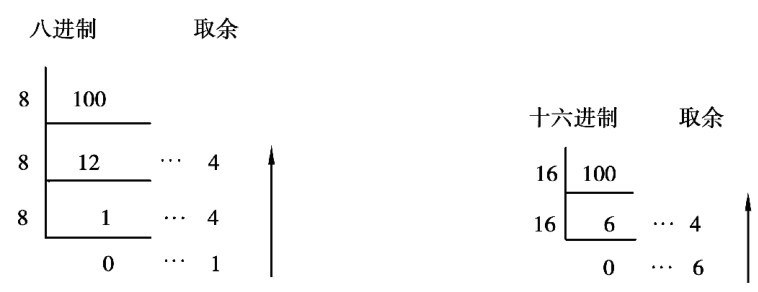
整数部分：连续除以基数R，直到商为0为止，再逆序取各位余数。

小数部分：连续乘基数R，直到积为整数为止，再顺序取各位整数。

例如：

（100．6875）10＝（1100100．1011）2

（100）10＝（144）8＝（64）16

2．2．2 R进制数转换成十进制数

按权位展开，依次相加。加权公式如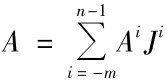：其中n为整数位数（最低位为0位），m为小数位数，Ai为该数A的第i位数字，J为进制数，Ji为该数第i位的权。例如：

（101101）2＝1×25＋0×24＋1×23＋1×22＋0×21＋1×20＝45

（23．4）8＝2×81＋3×80＋4×8－1＝19．5

（1D9）16＝1×162＋13×161＋9×160＝473

2．2．3 二进制数与八进制数、十六进制数之间的转换

二进制数、八进制数和十六进制数之间的相互转换很有实用价值。 由于这3种进制的权之间有内在的联系，即23＝8，24＝16，因而它们之间的转换比较容易，即每位八进制数相当于3位二进制数，每位十六进制数相当于4位二进制数。

在转换时，位组划分是以小数点为中心向左右两边进行的，中间的0不能省略，两头不足时可以补0。 例如：

（11010．110101）2＝（011010．110101）2＝（32．65）8

（11010．110101）2＝（00011010．11010100）2＝（1A．D4）16

（32）8＝（011010）2＝（11010）2

（1A）16＝（00011010）2＝（11010）2

如果要将八进制数转换成等值的十六进制数，可以先将八进制数转换成二进制数，再把二进制数转换成十六进制数，反之亦然。例如，（32）8＝（11010）2＝（1A）16。

有时，为了表示方便，常用字母B，O，D和H分别来表示二进制、八进制、十进制和十六进制数。如，（10011）2可表示为10011B，（9A）16可表示为9AH。