2.3 计算机中数据的表示
2.3 计算机中数据的表示
在计算机内部,所有的信息(包括数据和指令)都采用二进制编码来表示,而二进制描述的计算机存储单位是位。 现在我们来看一下计算机中信息表示的单位。
(1)位(bit)
位是二进制数位的缩写,在计算机中bit指二进制的一个位数,简称b。 以0和1来表示。位是计算机信息的最小存储单位。
(2)字节(Byte)
字节是由若干个二进制位的组成,简称B。 一个字节通常由8个二进制位组成,即1Byte=8bit。 字节是在信息技术和数码技术中用于表示信息的基本存储单位。
由于字节这个单位比较小,因此常用的信息组织和存储容量单位实际上是KB、MB、GB、TB等,它们之间以1024为进制单位。
•1KB=210B=1024B
•1MB=220B=1024KB
•1GB=230B=1024MB
•1TB=240B=1024GB
(3)字(Word)
字是其用来一次性处理事务的一个固定长度的位(bit)组,是计算机存储、传输、处理数据的信息单位。 字是计算机进行信息交换、处理、存储的基本单元。 字是由若干个字节组合。1Word=n Byte。
(4)字长
在同一时间中处理二进制数的位数称为字长。 例如,CPU和内存之间的数据传送单位通常是一个字长;还有内存中用于指明一个存储位置的地址也经常是以字长为单位的。 通常称处理字长为8位数据的CPU为8位CPU,32位CPU就是在同一时间内处理字长为32位的二进制数据。 现代计算机的字长通常为16,32,64位。
2.3.1 数值数据在计算机内的表示
数值数据有正有负,在计算机中表示一个数值数据时,总是用最高位表示数值的符号,其中“0”表示正,“1”表示负,其他各位表示数的大小。 在计算机中,小数点位置固定的数称为定点数。 通常,计算机中的定点数有两种:定点整数和定点小数。
在讲述上述两个内容之前不得不先引入两个非常重要的概念:原码和补码。
①原码。 原码是一种计算机中对数字的二进制定点表示方法。 原码表示法在数值前面增加了一位符号位(即最高位为符号位):正数该位为0,负数该位为1(0有两种表示:+0和-0),其余位表示数值的大小。
例如,用8位二进制表示一个数,+11的原码为00001011,-11的原码就是10001011。
原码不能直接参加运算,可能会出错。 例如数学上,1+(-1) =0,而在二进制中00000010+10000010=10000100,换算成十进制为-4。 显然出错了。 出错的原因是符号位也直接参与了计算。 为了解决这个问题,在计算机中提出了补码表示数据的方式。
②补码。 在计算机系统中,数值数据一律用补码来表示(存储)。 主要原因:使用补码,可以将符号位和其他位统一处理;同时,减法也可按加法来处理。 另外,两个用补码表示的数相加时,如果最高位(符号位)有进位,则进位被舍弃。 另外,补码与原码的转换过程几乎是相同的。
正数的补码与原码相同。
例如:+10的补码是00001010。
负数的补码等于其原码的符号位不变,数值部分的各位取反,然后整个数加1。
例如:求-10的补码。
-10的原码(10001010)→符号位不变,按位取反(11110101)→整个数加1(11110110)。
1)定点整数
定点整数的小数点默认为在二进制数最后一位的后面。 在计算机中,正整数是以原码(即二进制代码本身)的形式存储的,负整数则是以补码的形式存储的。
假设用8个二进制(一个字节)来存储整数,则将0符号化后用原码表示为:
+0=00000000 -0=10000000
可见,二者并不一致。 因此,必须想办法使0的表示方法唯一。
对负整数求补码,如:
-0→10000000(原码)→11111111(反码)→11111111+1→00000000(补码)
正整数的补码与原码相同。
采用补码表示整数的另一个好处是运算时不需要单独处理符号位,符号位可以像数值一样参与运算。 如:求10-5=?
[10]补=00001010 [-5]补=11111011
[10]补+[-5]补=00001010+11111011=00000101(最高进位甩掉)
补码运算的结果仍为补码,再将补码转换回原码,即可得到运算的结果,如上例的运算结果为5(因为结果为正数,故补码就是原码)。 如果运算结果为负数,可以用减1再取反(符号位不变)的逆过程求出原码。 如:求5-10=?
[5]补=00000101 [-10]补=11110110
[5]补+[-10]补=00000101+11110110=11111011
将11111011减1再将除符号位外的其他位取反,可得原码为10000101,即-5。
2)定点小数
定点小数的小数点默认为在二进制数的最高位(即符号位)后面。 在计算机中,既有整数部分又有小数部分的数称为浮点数。 浮点数分为单精度(32位)、双精度(64位)和扩展精度(80位)3种。
浮点数采用尾数和阶码的形式存储,即阶码符号、阶码、尾数符号和尾数分别存储在单独的位置,阶码的位数决定了这个数的大小,尾数的位数决定了这个数的精度。

例如,一个十进制浮点数为6.375,转换成二进制数为110.011,写成二进制的指数形式为0.110011×2+11(注意,这里的阶码11为二进制数),存储在计算机中的形式如下:

浮点数的运算比较复杂,为了提高运算速度,在计算机硬件中一般都专门设有浮点运算部件。
2.3.2 字符数据在计算机中的表示
计算机中的非数值信息也采用0和1两个符号的编码来表示。
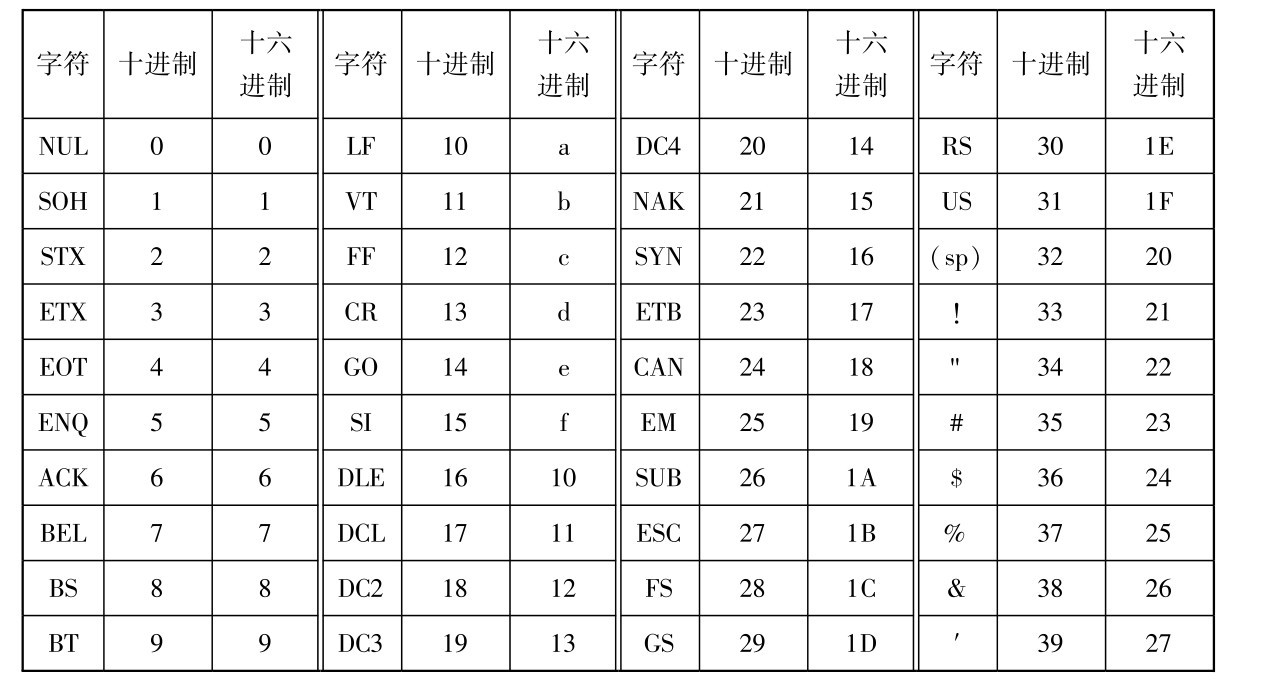
目前,微型计算机中普遍采用的英文字符编码是ASCII码(American Standard Codefor In⁃formation Interchange,美国国家标准信息交换码)。 它采用一个字节来表示一个字符,在这个字节中,最高位为0(零),低7位为字符编码,00000000~01111111(0~127)共代表了128个字符,见表2.3。
表2.3 标准7位ASCII码字符集
续表
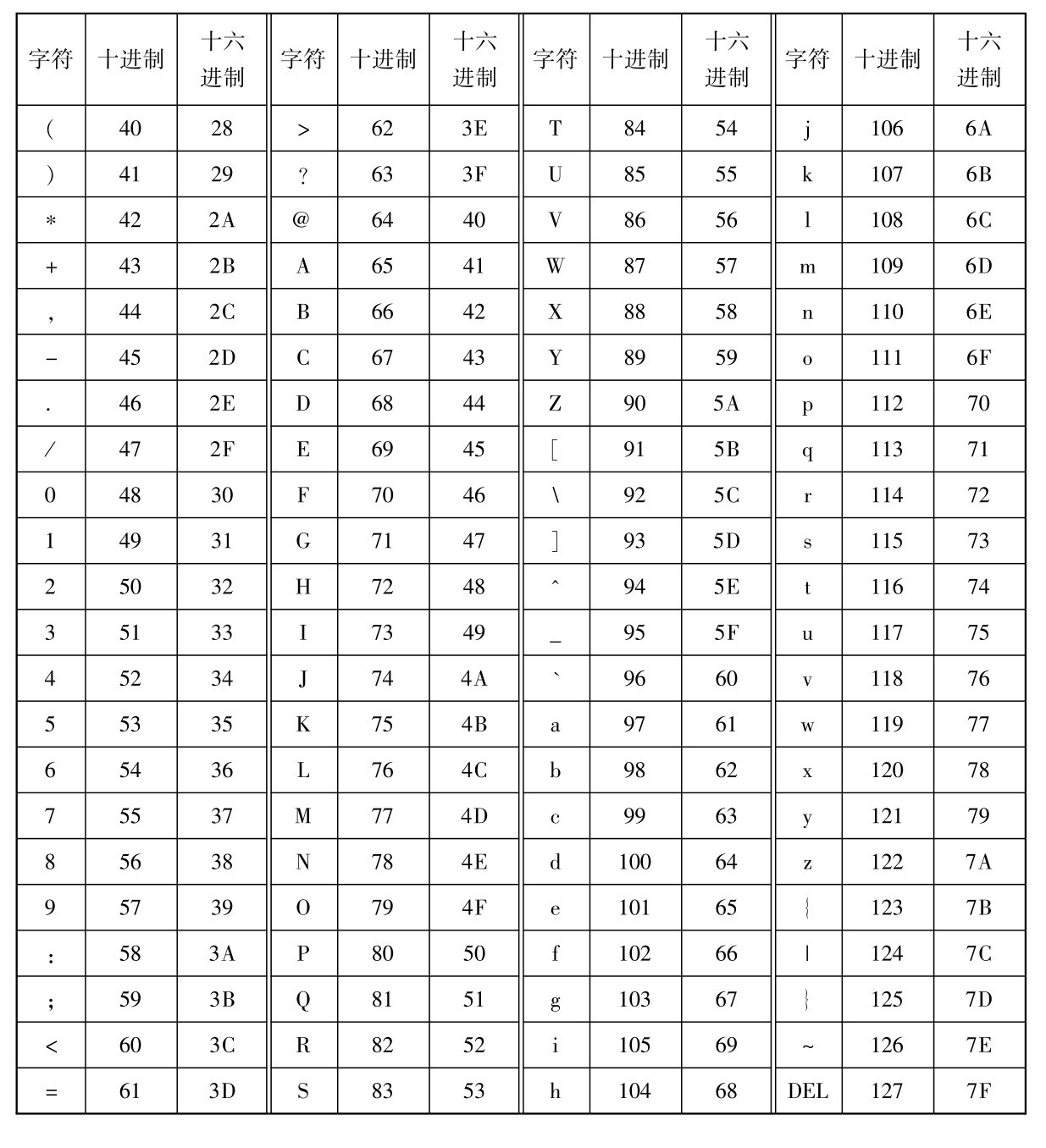
在这128个ASCII码字符中,编码0~31是32个不可打印和显示的控制字符,其余96个编码则对应着键盘上的字符。 除编码32和128这两个字符不能显示出来之外,另外94个字符均为可以显示的字符。 从表2.3中可以看出以下规律:
①数字0的ASCII码是48D或30H;大写字母A的ASCII码是65D或41H;小写字母a的ASCII码是97D或61H。
②数字0~9、大写字母A~Z、小写字母a~z的ASCII码值是连续的。 因此,如果知道了数字0、大写字母A和小写字母a的ASCII码值,就可以推算出所有数字和字母的ASCII码值。例如,A的ASCII码为1000001,对应的十进制数是65,由A~Z编码连续可以推算出字母D的ASCII码是68(十进制数)。
③数字0~9的ASCII码值小于所有字母的ASCII码值;大写字母的ASCII码值小于小写字母的ASCII码值;大写字母与其对应的小写字母之间的ASCII码值之差正好是十进制数32。
2.3.3 中文字符在计算机中的表示
汉字符号比西文符号复杂得多,所以汉字符号的编码也比西文符号的编码复杂得多。 首先,汉字符号的数量远远多于西文符号,汉字有几万个字符,就是国家标准局公布的常用汉字也有6763个(常用的一级汉字3755个,二级汉字3008个)。一个字节只能编码28=256个符号,用一个字节给汉字编码显然是不够的,所以汉字的编码用了两个字节。 其次,这么多的汉字编码让人很难记忆。 为了使用户方便迅速地输入汉字字符,人们根据汉字的字形或者发音设计了很多种输入编码方案,来帮助人们记忆汉字的编码。 为了在不同的汉字信息处理系统之间进行汉字信息的交换,国家专门制定了汉字交换码,又称国标码,国标码在计算机内部存储时所采用的统一表达方式被称为汉字内码。 无论是用哪一种输入编码方法输入的汉字,都将转换为汉字内码存储在计算机内。
综上所述,汉字的编码有3类:输入编码、内部码和字形码。 这3类汉字编码之间的关系如图2.1所示。
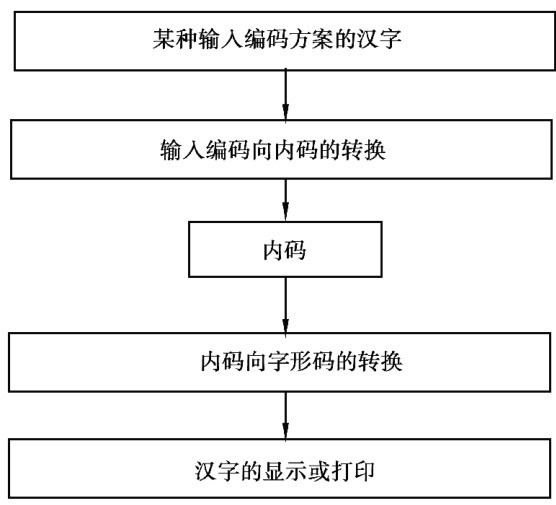
图2.1 各汉字编码之间的关系
1)输入码
汉字的输入方式目前仍然是以键盘输入为主,而且是采用西文的计算机标准键盘来输入汉字,因此汉字的输入码就是一种用计算机标准键盘按键的不同组合输入汉字而编制的编码。人们希望能找到一种好学、易记、重码率低并且快速简捷的输入编码法。 目前已经有几百种汉字输入编码方案,在这些编码方案中一般大致可以分为3类:数字编码、拼音码和字形编码。
(1)数字编码
数字编码就是用数字串代表一个汉字的输入,常用的是国标区位码。 例如,“中”字位于第54区48位,区位码为5448。 数字编码输入的优点是无重码,而且输入码和内部编码的转换比较方便,但是每个编码都是等长的数字串,难以记忆,因此目前较少使用。
(2)拼音码
拼音码是以汉语读音为基础的输入法。 由于汉字同音字太多,输入重码率较高,因此,按拼音输入后还必须进行同音字选择,影响了输入速度。 目前大部分的汉字输入都采用这种输入方式,比较常用的输入法有:谷歌拼音输入法、搜狗拼音输入法等,如图2.2所示。

图2.2 谷歌拼音输入法和搜狗拼音输入法
(3)字形编码
字形编码是以汉字的形状确定的编码。 汉字总数虽多,但都是由一笔一画组成的,全部汉字的部首和笔画是有限的。 因此,把汉字的笔画部首用字母或数字进行编码,按笔画书写的顺序依次输入,就能表示一个汉字。 五笔字型编码是最有影响的字形编码方法,比较常用的输入法有:万能五笔输入法、王码五笔型输入法、陈桥五笔输入法和极品五笔输入法等。
2)内部码
世界各大计算机公司一般均以ASCII码为内部码来设计计算机系统。 汉字数量多,用一个字节无法区分,一般用两个字节来存放汉字机内码。 汉字机内码又称内码,对于汉字存储和处理来说,汉字较多,要用两个字节来存放汉字的机内码。 为了避免与高位为0的ASCII码相混淆,根据GB3212—80的规定,每字节最高位为1,这样内码和外码就有了简单的对应关系,同时也解决了中、英文信息的兼容处理问题。 例如,以汉字“啊”为例,其国标码为3021(H),机内码为B0A1(H)。
3)字形码
把汉字写在划分成m行n列小方格的网络方格中,该方阵称当m×n点阵。 每个小方格是一个点,有笔画部分是黑点,文字的背景部分是白点,点阵中的黑点就描绘出汉字字形,称为汉字点阵字形(见图2.3(a))。 用1表示黑点,0表示白点,按照自上而下、从左至右的顺序排列起来,就把字形转换成了一串二进制的数字(见图2.3(b))。 这就是点阵汉字字形的数字化,即汉字字形码。 字形码也称为字模码,它是汉字的输出形式,根据输出汉字的要求不同,点阵的多少也不同。 常用的汉字点阵方案有16×16点阵、24×24点阵、32×32点阵和48×48点阵等。 以16×16点阵为例,每个汉字要占用32个字节,两级常用汉字大约占用256KB。一个汉字信息系统具有的所有汉字字形码的集合就构成了该系统的字库。
汉字输出时经常要使用汉字的点阵字形,因此,把各个汉字的字形码以汉字库的形式存储起来。 但是汉字的点阵字形的缺点是放大后会出现锯齿现象,很不美观,而且汉字字形点阵所占用的存储空间比较大,要解决这个问题,一般采用压缩技术,其中矢量轮廓字形法压缩比大,能保证字符质量,是当今最流行的一种方法。 矢量轮廓先定义加上一些指示横宽、竖宽、基点和基线等控制信息,就构成了字符的压缩数据。
轮廓字形方法(见图2.3(c))比点阵字形复杂,一个汉字中笔画的轮廓可用一组曲线来勾画,它采用数学方法来描述每个汉字的轮廓曲线。 中文Windows操作系统下广泛采用的True Type字形库就是采用轮廓字形法。 这种方法的优点是字形精度高,且可以任意放大或缩小而不产生锯齿现象。
4)其他汉字编码
(1)GBK码
GBK码是中国制定的新的中文编码扩展国家标准。 该编码标准兼容GB2312—1980,共收录汉字21003个,符号883个,并提供1894个造字码位,将简、繁体字融于一库。
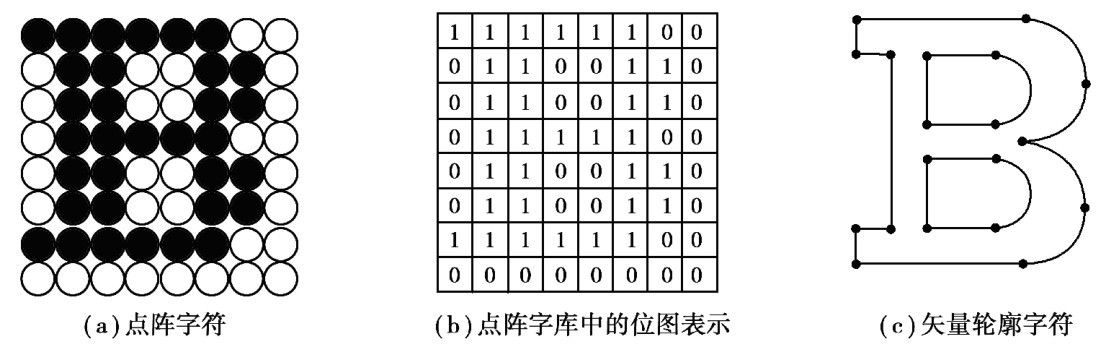
图2.3 汉字字形码的表示方法
(2)BIG5码
BIG5码包含420个图形符号和13070个汉字,但不包括简化汉字。
(3)Unicode码
Unicode码是统一编码组织于20世纪90年代制定的一种16位字符编码标准,它以两个字节表示一个字符,世界上几乎所有的书面语言都可以用这种编码来唯一表示,其中也包括中文。 目前,Unicode码已经成为信息编码的一个国际标准,在它的65536个可能的编码中,对39000个编码已经作了规定,其中21000个编码用于表示汉字。 Microsoft Office就是一个基于Unicode文字编码标准的软件,无论使用何种语言编写的文档,只要操作系统支持该语言的字符,Office都能正确识别和显示文档内容。
