2.4  双馈感应发电机建模

2.4 双馈感应发电机建模

由于双馈感应发电机是一个多变量、强耦合、非线性、时变的高阶系统，为了便于分析，通常作如下假设^[3]：

1）忽略空间谐波，假设三相绕组对称且在空间相差120°，所产生的磁动势按正弦规律分布。

2）忽略磁路非线性饱和，假设各绕组的自感和互感都为定值。

3）忽略铁心损耗。

4）忽略频率变化和温度变化对绕组电阻的影响。

5）若无特别说明，转子侧的参数都是折算到定子侧，折算后的定子和转子绕组匝数相同。

在以同步转速ω₀旋转的d-q-0坐标系下，不计零轴分量，双馈感应发电机的定、转子绕组均采用电动机惯例，建立双馈感应发电机数学模型。

1）磁链方程

式中，L_ss=L_s+L_m，L_rr=L_r+L_m；Ψ_sd、Ψ_sq分别为定子磁链的d、q轴分量；Ψ_rd、Ψ_rd分别为转子磁链的d、q轴分量；i_sd、i_sq分别为发电机定子电流的d、q轴分量；i_rd、i_rq分别为转子电流的d、q轴分量；L_s、L_r分别为定子、转子的漏感；L_m为定子和转子之间的互感。

2）电压方程

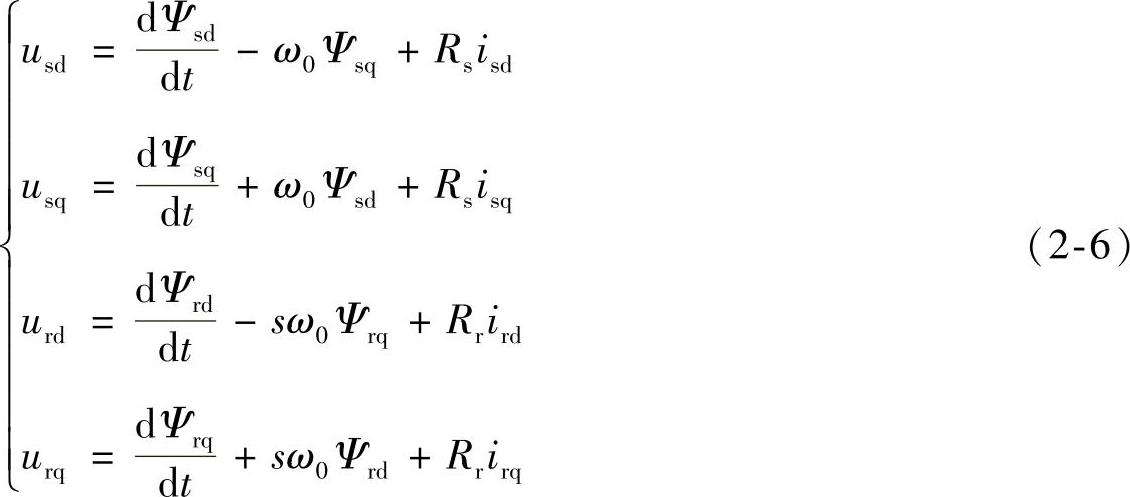
式中，u_sd、u_sq分别为发电机定子电压的d、q轴分量；u_rd、u_rq分别为转子电压的d、q轴分量；R_s、R_r分别为发电机定、转子电阻；s为转差率。

3）电磁转矩方程

T_e =n_pL_m（i_sqi_rd-i_sdi_rq） （2-7）

式中，n_p为发电机的极对数。

式（2-5）～式（2-7）为双馈感应发电机的基本方程。为了研究方便，忽略定子绕组暂态，并设d、q轴参数对称，推导得出的双馈感应发电机简化实用动态等效模型为

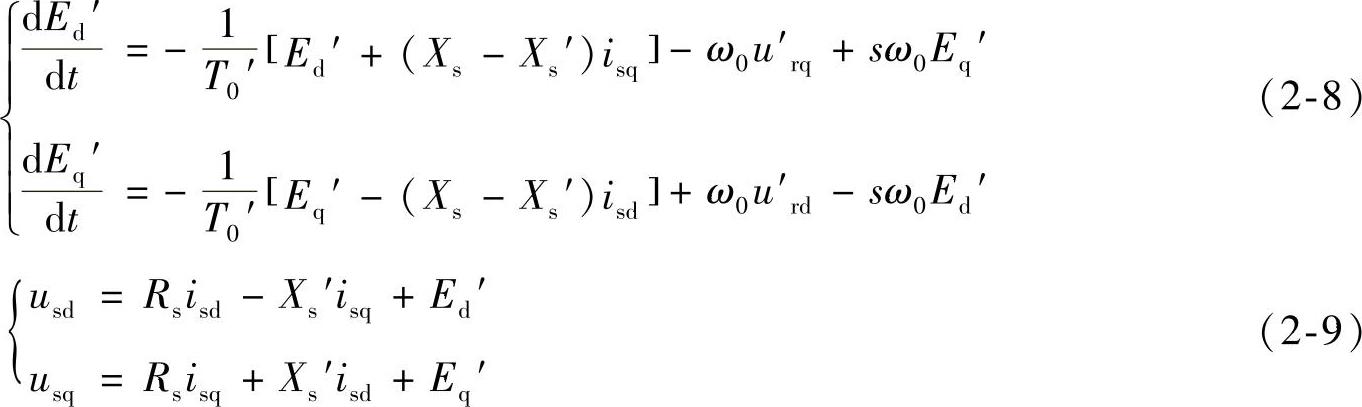
式（2-8）、式（2-9）中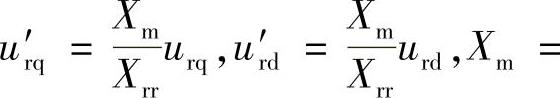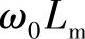，，X_rr=ω₀L_rr；E_d′、E_q′分别为发电机等效暂态电动势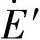的d、q轴分量；T′₀为定子开路时转子回路的时间常数；R_s为定子电阻；X′_s为暂态电抗；X_s为定子同步电抗。

用发电机等效暂态电动势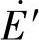和暂态阻抗R_s+jX′_s表示的等效电路如图2-3所示。

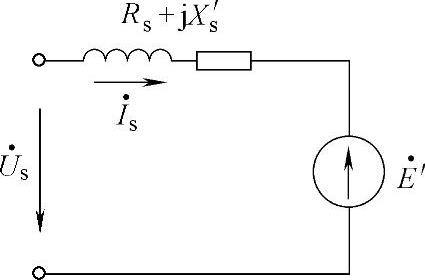
图2-3 用发电机等效暂态电动势和暂态阻抗表示的等效电路