7.3.2 故障电流频率偏移对风电场主变压器差动保护的影响
1.对相量值差动保护的影响
基于相量值的变压器差动保护如图7-4所示,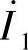 、
、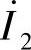 为变压器两侧二次电流的相量值。
为变压器两侧二次电流的相量值。
两侧不同频率正弦电流i1、i2分别为
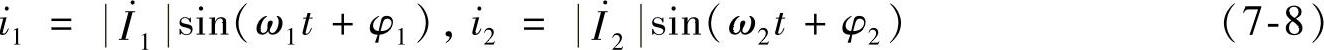
式中,ω1、ω2分别为变压器两侧二次电流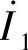 、
、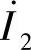 的角频率。
的角频率。
两正弦电流对应的相量按各自频率旋转,幅值为
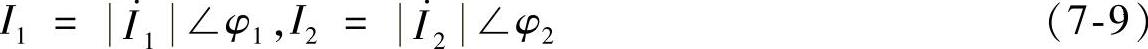
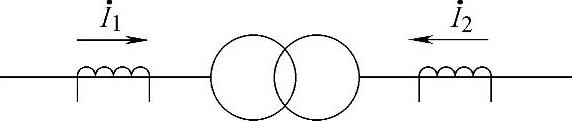
图7-4 基于相量值的变压器差动保护
利用基于信号基频的傅里叶算法可以准确获取两电流基频相量,进而可由式(7-3)、式(7-4)求取稳定的差动与制动电流。但是在微机继电保护中,常利用基于工频分量的傅里叶算法(简称傅里叶工频算法)实现信号基频相量的测量与计算。当信号频率发生偏移时,其固定的采样频率在一个采样周期内采到的点数N′不再等于N(N为一个周期内工频信号采样点数,本文取N=24),工频傅里叶数字滤波器的输出性能就会变差,相应的保护算法将会产生很大的误差。信号频率偏移时,傅里叶工频算法无法准确提取基频相量,差动保护算法也将会产生很大误差。
为分析方便,令式(7-8)两正弦电流幅值均为1,i1角频率为工频ω1,i2角频率ω2=λω1偏移工频。利用傅里叶工频算法分别求取两电流基频相量后,可得差动保护动作电流Iop,即
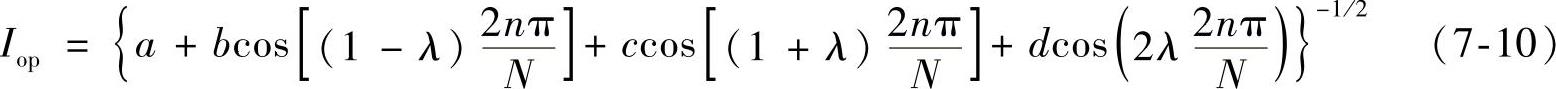 (https://www.daowen.com)
(https://www.daowen.com)
式中,a、b、c、d均为常数,大小取决于电流频率偏移系数λ。
此时差动保护动作电流不再是恒定值,而是另外叠加了三个频率分量的变化值,即(1-λ)f1、(1+λ)f1和2λf1。由于b值一般较大,因此当λ在1附近变化时,信号频率与工频的差值频率电流为差动保护动作电流的主要构成部分。下面取λ=0.8,对工频和40Hz正弦电流作差动分析,动作电流如图7-5中实线所示。动作电流不再保持恒定,主要构成分量为信号频率与工频的差值频率(即10Hz)分量,同时叠加了(1+λ)f1=90Hz和2λf1=80Hz频率分量。类似地可以得到该情况下的制动电流的变化规律,如图7-5中虚线所示。由于两侧频率偏移时,基于相量值的差动保护动作电流与制动电流将以多个频率分量大范围波动,不再类似传统工频电流差动保持稳定,因此,若按此动作特性整定差动保护,将无法保证准确稳定地动作。
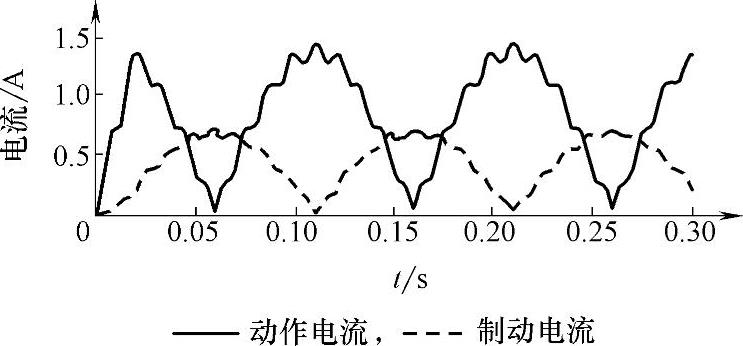
图7-5 相量值差动保护的动作电流与制动电流
同理,两侧频率偏移时,利用傅里叶工频算法也无法准确提取差动电流中的二次谐波,二次谐波分量将被傅里叶工频算法放大,致使比率差动保护被制动元件闭锁。
2.对采样值差动保护的影响
基于采样值的变压器差动保护只需将图7-4中相量值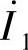 、
、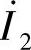 换为瞬时采样值i1(n)、i2(n)。采样值差动保护动作电流iop(n)与制动电流ires(n)分别为
换为瞬时采样值i1(n)、i2(n)。采样值差动保护动作电流iop(n)与制动电流ires(n)分别为
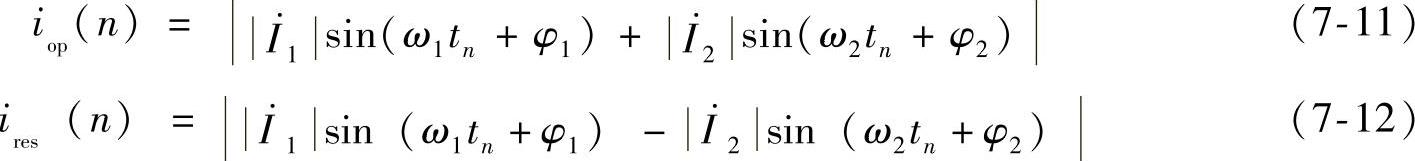
为分析方便,仍令式(7-8)两正弦电流幅值为1,i1角频率为工频ω1,i2角频率ω2=λω1偏移工频,取λ=0.8,采样值差动保护的动作电流与制动电流如图7-6所示,其变化频率为10Hz,取决于两电流频率的关系。
传统工频量的采样值差动保护连续取R次,判别S次满足判据即可以可靠动作。由于两侧频率偏移时,采样值差动保护动作电流频率非工频,除在差流过零点附近不满足动作条件外,其他采样点差流很小,也可能不满足动作条件,因此若按此动作特性整定差动保护,也无法保证准确稳定地动作。
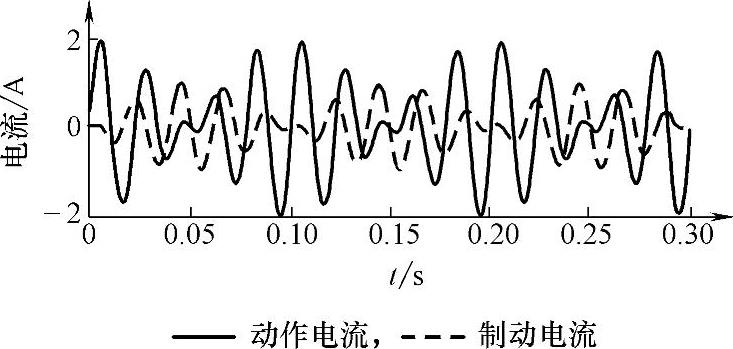
图7-6 采样值差动保护的动作电流与制动电流
