5.1.4 多元线性回归模型的应用
前面已经介绍了多元线性回归模型的一些基本知识和常用的R函数。本小节将结合一个实例详细介绍多元线性回归模型的应用过程。
计量经济学涉及多学科知识,是一门比较难的学科。某大学老师想要探究学生计量经济学考试成绩与其他影响因素之间的关系。根据初步的分析,他认为微积分成绩、线性代数成绩、统计学成绩、大学计算机基础成绩和西方经济学成绩是影响计量经济学成绩的主要因素,并随机抽样了30个学生的成绩,如表5-1所示。其中,y表示计量经济学成绩;x 1表示微积分成绩;x 2表示线性代数成绩;x 3表示统计学成绩;x 4表示大学计算机基础成绩;x 5表示西方经济学成绩。
表5-1 随机抽样得到的30个学生的考试成绩
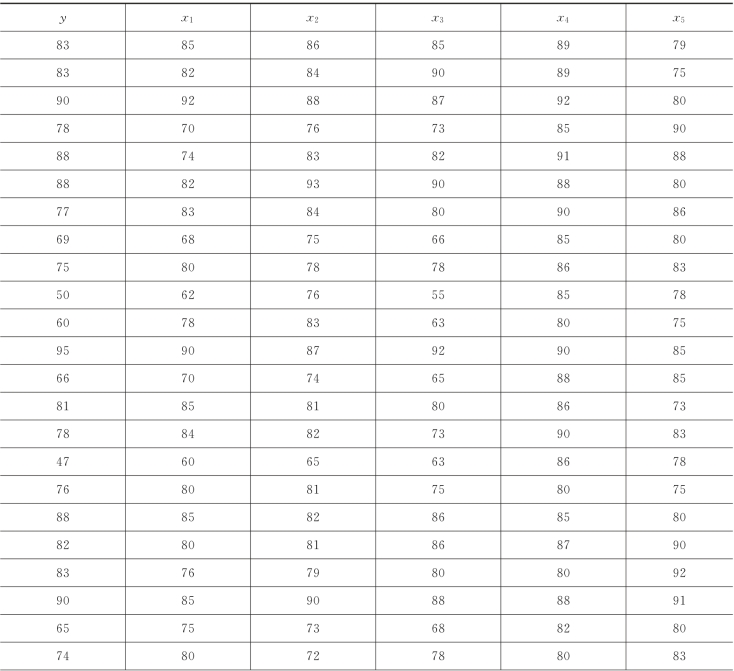
续表
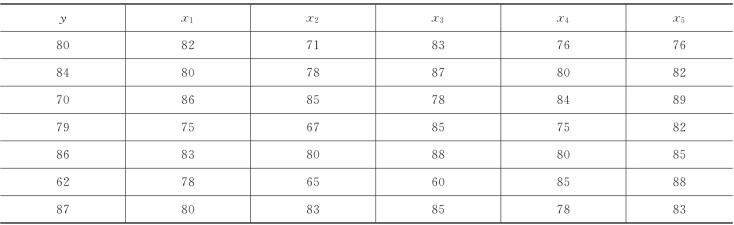
多元线性回归模型的应用步骤如下。
(1)确定因变量和自变量,并收集相关数据,如表5-1所示。
(2)对因变量与自变量进行相关分析,设定理论模型。用R中的cor()函数计算增广相关系数矩阵,代码如下:
代码输出结果如图5-2所示。
图5-2 相关分析输出结果
从相关分析输出结果可以看到,y与x 1、x 2,x 3的相关系数都在0.6以上,这说明自变量与因变量是比较相关的,用当前的自变量与因变量进行多元线性回归分析是合理的。y与x 4、x 5的相关系数较小,分别为0.16和0.23左右,通过计算,其P值均为0.9以上,这说明计算机基础成绩和西方经济学成绩对计量经济学成绩无显著影响。然而,仅凭相关系数的大小并不能决定相关变量的取舍,因此,在初步建模时也应该包含x 4和x 5。
(3)使用R中的lm()函数进行多元线性回归分析,构建回归方程,对应代码如下:
代码输出结果如图5-3所示。
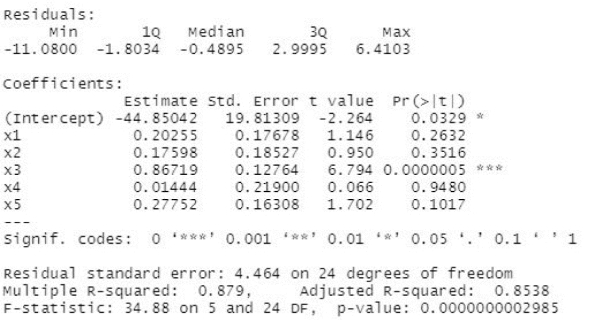
图5-3 多元线性回归模型输出结果
(4)回归诊断。
①通过输出结果可知,回归方程为
②通过输出结果可知,决定系数R 2＝0.879,因此,得出的回归方程是高度显著的。
③通过输出结果可知,回归模型整体方差检验值F＝34.88,检验显著性值P＝2.985×10－10,这表明回归方程整体上高度显著。
④回归系数显著性检验结果表明,只有x 3对y有显著影响,但是不能简单认为其他变量对自变量没有影响,因此,在实际分析中应该进一步讨论。
(5)模型应用。
给定因变量x 1＝80,x 2＝60,x 3＝90,x 4＝75,x 5＝88,利用上述回归模型对y进行预测,代码如下:
得到的点预测和区间预测结果如下:
代码中的interval＝“prediction”表示需要给出区间预测,level＝0.95表示置信区间为95%。计算结果表明,点预测值为85.464,区间预测结果为[73.293,97.635]。