5.2.2　logistic回归模型的应用

5.2.2　logistic回归模型的应用

本小节介绍logistic回归模型的应用,以调查得到的180个不同年龄的人对同一部影片的观点为例,如表5-2所示。其中,No表示样本编号,x表示观众的年龄,y表示观众对该影片的观点(y为二分类变量,1和0分别表示肯定和否定观点)。以观众对影片的观点y为因变量,观众的年龄x为自变量,构建logistic回归模型,并估计年龄为25岁的观众对该影片持肯定观点的可能性。

表5-2　不同年龄的观众对某影片的观点

续表

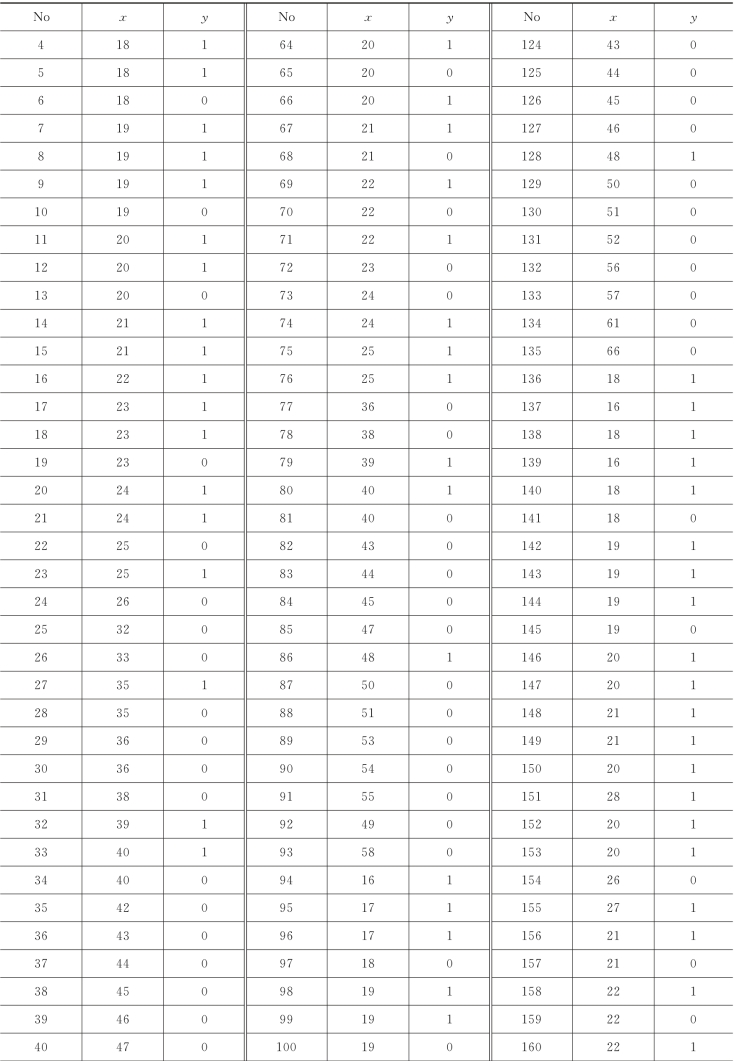
续表

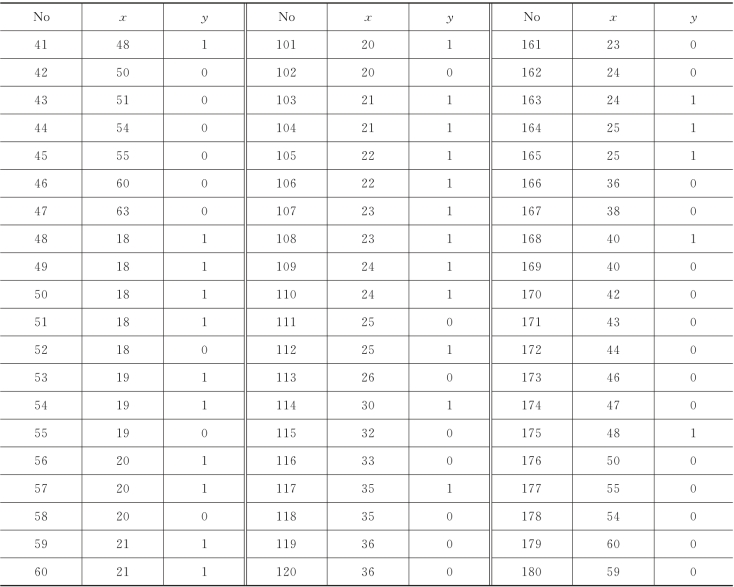
logistic回归模型的应用步骤如下。

(1)确定自变量和因变量,本例中x为自变量,y为因变量。

(2)使用R中的glm()函数拟合logit回归模型、估算回归系数,并对模型的回归系数进行显著性检验,代码如下:

运行上述代码,可得到logistic回归模型的输出结果,如图5-4所示。通过输出结果发现,回归系数对应的P值均在0.1%的水平上显著,这里需要注意的是,回归系数对应的P值越小,统计性越显著,一般认为P值小于0.05是显著的。在结果中,“*”表示在5%水平上显著;“**”表示在1%水平上显著;“***”表示在0.1%水平上显著。

因此,本例的回归模型为ln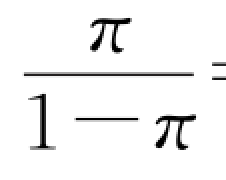＝3.634－0.123x。

(3)使用predict()函数和回归模型,估计年龄为25岁的观众对该影片持肯定观点的可能性,代码如下:

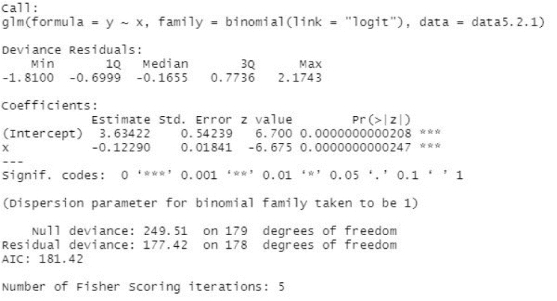
图5-4　logistic回归模型输出结果

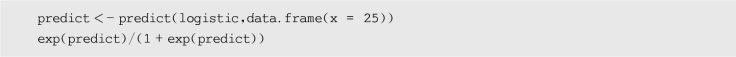
运行上述代码,得到的结果如下:

由运行结果可知,当x＝25时,y＝1的概率约为0.636 9,因此,年龄为25岁的观众对该影片持肯定观点的可能性约为63.69%。