贺兰口待抢救保护岩画危岩情况调查
一、调查范围和目的
岩体稳定性调查范围主要是针对本次岩画保护范围内的岩体而进行的。调查目的包括:
(1)统计裂隙产状,绘制岩体裂隙分布图;
(2)了解岩体结构,寻找控制岩体稳定性的关键结构面;
(3)分析可能存在的危岩类型,判断失稳模式;
(4)针对岩画和危岩特点,提出危岩加固的初步设想。
二、岩体裂隙现状和分布图
为了了解岩体结构面发育的宏观规律性,揭示岩体结构特征,以便有效地了解贺兰山贺兰口沟口附近岩体力学特性,指导危岩稳定性计算,本次在野外岩体裂隙测量基础上,利用Dips软件进行了岩体裂隙统计。
(一)测量范围
裂隙测量主要集中在贺兰口沟口处岩画附近的岩体,包括“驴羊图”“圣像壁”“鹿与马”“人面动物组合”“牧猎图”“睁一只眼闭一只眼”“手印图”“太阳神”以及“人面群像”等岩画(见图1—图4)。
对研究区内出露的基岩进行野外结构面的统计,以此为样本,得到结构面分布散点图(见图5)、结构面等密度图(见图6)及结构面走向玫瑰花图(见图7)。

图1 人面动物组合岩画西侧岩体

图2 牧猎图岩画底部岩体

图3 太阳神岩画东侧底部岩体

图4 太阳神岩画顶部岩体
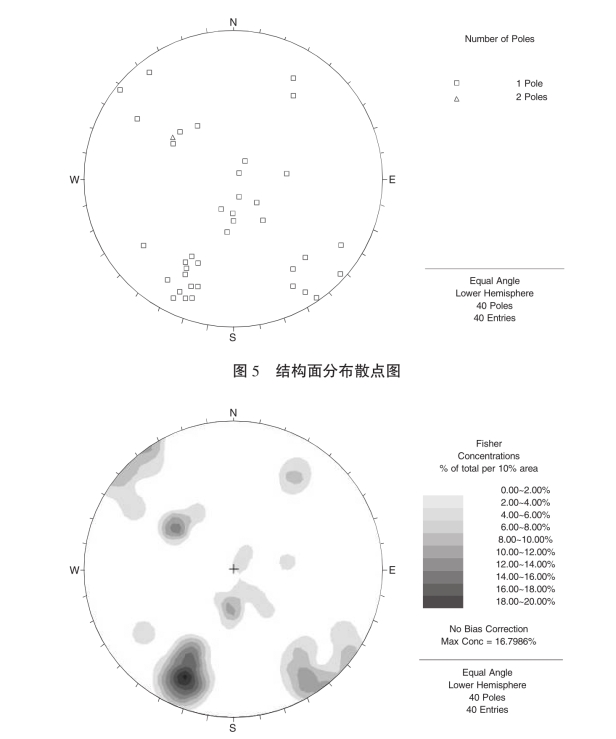
图6 结构面等密度图
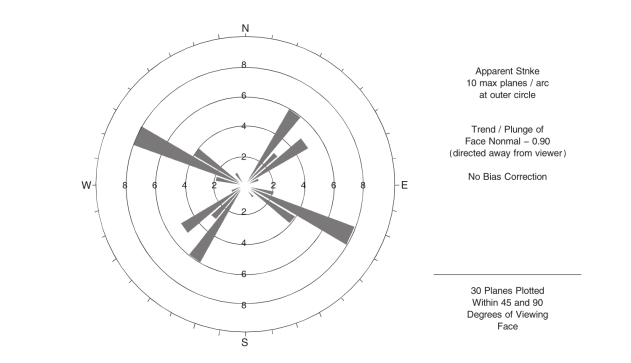
图7 结构面走向玫瑰花图
三、岩体地质病害调查
对贺兰口岩画进行岩体地质病害调查,主要目的是:
(1)了解岩画所在岩体的岩体结构类型;
(2)分析岩画所面临的主要地质病害;
(3)判断周围是否存在危岩及其稳定性分析。
(一)岩体结构类型
表3 岩体结构类型
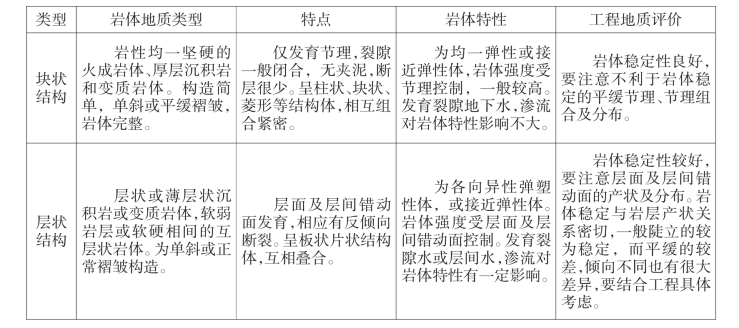
控制岩体稳定性除了地形地貌、地质构造和地层岩性外,岩体结构也是重要的一个方面,因为岩体的破坏不仅是材料破坏,许多情况下是结构失稳[2]。岩体结构因素包括结构面的组数和数量、结构面的倾角和倾向、结构面的连续性以及结构面的表面性质等。根据前人的研究,岩体结构主要分为四类:整体块状结构、层状结构、碎裂结构和散体结构[3](见表3),不同类型岩体结构破坏方式也不同。
续表
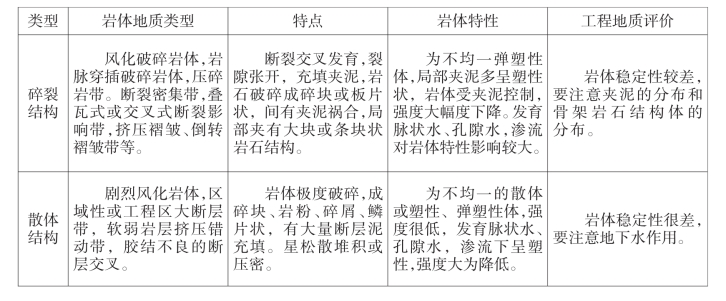
此外,对岩画而言还必须考虑到岩体表面微裂隙。因为随着雨水、温差等风化作用会使这些微裂隙扩展和连通,岩体表面遂沿着裂隙产生剥落和变形,造成岩画模糊或者脱落。
(二)危岩体类型
迄今为止,不同研究对危岩的分类有很多种。从工程防治角度对危岩进行失稳分类可以概括成坠落式危岩、滑塌式危岩和倾倒式危岩3类[4](见图8)。
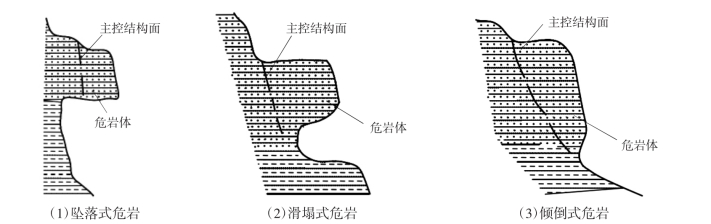
图8 危岩体类型[5]
坠落式危岩的危岩体下部受结构面切割脱离母岩,上部及后部与母岩尚未完全脱离。危岩体底部临空,临空的原因或者是由于危岩体下部软岩的快速风化而成岩腔,或者是由于下部先期危岩体崩落后的渐进发育,属于主控结构面剪切滑移失稳。滑塌式危岩的危岩体后部存在与边坡倾斜一致的贯通或断续贯通的主控结构面,倾角较缓,剪出部位多数出现在陡崖或斜坡,也可能出现在危岩体基座岩土体中,危岩体沿着主控结构面剪切滑移失稳。倾倒式危岩的危岩体后部存在与边坡坡向一致的陡倾角贯通或断续贯通的主控结构面,危岩体底部局部临空,危岩体重心多数情况下出现在基座临空支点外侧,支点为中风化岩层外缘点,危岩体可能围绕支点向临空方向旋转倾倒破坏[6]。
坠落式危岩的破坏机理主要体现在主控结构面的剪切破坏方面,滑塌式危岩则是在荷载作用下主控结构面以压剪破坏为主,倾倒式危岩的破坏机理主要表现为主控结构面在荷载作用下的拉剪破坏[7]。
(三)危岩体稳定性判别方法
1.失稳模式
从广义上讲,危岩体失稳模式是将岩体地质模型、几何模型和力学模型结合,通过适当简化、分类和数学推导来描述的一类危岩体破坏规则。迄今为止这方面的研究结果尚不统一,从工程实践角度出发,危岩体失稳模式应当概念明确和应用简便。陈洪凯等人将危岩体失稳模式分为坠落式、滑塌式和倾倒式三类,并从力学机理上将单体危岩变形破坏机制总结为压剪滑动、拉剪倾倒、拉裂坠落和拉裂压剪四类。其中,滑塌式危岩体主要为压剪滑动破坏,而坠落式和倾倒式危岩体则以拉剪倾倒、拉裂坠落和拉裂压剪破坏为主。
2.计算方法
危岩体稳定性的计算方法通常以极限平衡理论来推导。在极限平衡理论中,分别考虑危岩体所受不同荷载(包括重力、地震力、裂隙水压力)及其组合,然后利用不同计算方法得到稳定系数来表示危岩体的稳定性。在工程设计中使用静力解析法来计算稳定系数时,可以有以下三种方法:①主控结构面之上的抗剪强度和剪应力之比;②岩体抗拉强度与最大拉应力之比;③抗倾覆力矩与倾覆力矩之比。此外对于边界条件比较复杂而难以用静力解析法时,则可以考虑使用数值模拟计算方法(例如有限单元法)。当然此时未必能得到一个确定数值的稳定系数,但是通过危岩体的应力、应变等或者塑性区等关键参数的变化也可以判断其是否稳定。
(1)计算参数。由于稳定系数用不同方法得到,故所需岩体的力学参数也不相同:对于第①种方法而言,如果采用Mohr-Coulomb抗剪强度准则,则需要知道主控结构面上的内摩擦角和粘聚力;而对于第②和第③种方法而言,则需要知道岩体抗拉强度。计算参数应当依据现场和室内实验确定,在条件受到限制时可以采取一些经验强度准则来推导,但是必须注意使用条件和适用范围。
(2)经验强度准则。岩体及其主控结构面的强度参数通常是危岩体稳定性分析的关键参数,目前针对不同研究目的已经得到多种经验强度准则。结合本次实际情况将借鉴Hoek-Brown准则、贯通率法以及岩石表面回弹值进行估算。
(3)Hoek-Brown经验强度准则。Hoek-Brown经验强度准则是以试验结果为前提,以地质调查为基础,通过统计方法与经验参数相结合的半经验半理论的岩体强度公式。由于形式简便且具有一定理论依据因而应用较为广泛。该准则不仅适用于完整岩石,还适用于节理岩体,其强度参数通过现场地质调查并结合完整岩块单轴抗压强度所得,其最新的表达式为:
![]()
式中,σ1和σ3分别为最大和最小主应力,σci为完整岩块的单轴抗压强度,mb,s,α均为岩体强度参数,依赖于岩体的性质,可以利用(地质强度指标)来进行估算:
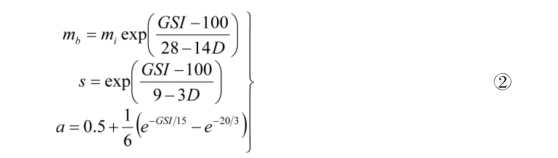
式中,为岩石材料常数,为工程因素影响系数(该值位于0-1之间,对于完整岩块时为0,对于受充分扰动的岩体时为1)的取值方法有很多种,具体内容可以参考相关文献。
(4)岩体单轴抗压强度。在式①中令,通过求解可以得到岩体单轴抗压强度:
![]()
(5)岩体单轴抗拉强度。在式①中令,通过求解则可以得到岩体单轴抗拉强度。通常情况下可以近似的认为,于是
![]()
(6)岩体变形模量。
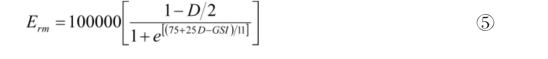
(7)贯通率法。为了估算主控结构面的强度参数,可以利用贯通率法进行估算。此时需要完整岩石的单轴抗压强度、内摩擦角以及裂隙贯通率。在缺乏必要的测试资料时也可由相关文献中的公式作为一般硬质岩石的主控结构面强度参数计算方法。根据研究结果,当裂隙贯通率超过50%时,危岩强度参数将急剧降低。
(8)岩石表面回弹值。如果没有完整岩石的单轴抗压强度和内摩擦角,却又必须做出定性的判断时,可以利用回弹仪对结构面或者附近岩石表面进行回弹实验,通过式④求得结构面基本内摩擦角:
![]()
必须指出的是,式⑥是在忽略剪胀角等影响因素的前提下得到的,并且只是一个经验公式,因而只能作为定性的判断依据,在贺兰口岩画地区还需进行更多的实验加以完善。
四、贺兰口危岩体稳定性分析
此次危岩体稳定性调查范围主要位于贺兰口沟口路边两侧的岩画附近。通过初步调查,在岩画本体附近共发育六处危岩体,分别位于“驴羊图”“鹿与马”“牧猎图”“手印图”“石坡岩画群”和“太阳神”岩画周围。危岩体体积1~20立方米不等,虽然体积不大,但由于靠近岩画(甚至自身表面就存在岩画),因此存在一定隐患。
(一)贺兰口岩石物理性质
从贺兰口岩画附近人工取样得到红色和绿色岩样若干块进行室内分析。利用OLYMPUSBH-2数码视频显微镜和日本理学公司的Dmax/rBX射线衍射仪分别进行岩相和矿物成分分析,结果显示岩样主要成分为石英,含少量长石、云母和方解石,因此判断岩石类型为石英砂岩。
参照GB/T9966.3-2001《天然饰面石材试验方法》中的第一和第二部分对岩样进行相关物理性能测试。其中强度测定条件为试样尺寸5×5×5厘米,并分别测定试样在自然风干状态以及在水中浸泡48小时饱和后状态下的单轴抗压强度,测定仪器为WDW-100电子万能材料试验机,每组6块。结果表明岩石真密度为2.77克/厘米3,体积密度为2.70克/厘米3,真气孔率为1.07%~2.53%,吸水率0.14。单轴干燥抗压强度196.5兆帕,单轴饱和抗压强度188.0兆帕,软化系数0.96。
(二)“驴羊图”岩画
“驴羊图”岩画位于贺兰口入口处南侧山壁(见图9),岩体属于块状结构,整体稳定状况较好。岩体共有三组裂隙:①252-292°/NE∠81°;②310°/SW∠16°;③55°/SE∠84°。三组裂隙间距5~40厘米不等,裂隙面紧闭,夹泥很少。在“驴羊图”岩画的西侧,岩体被②和③两组裂隙切割后形成不稳定结构,厚度0.6米,悬空面尺寸约1.2米×1.4米。
岩体底部已经坍塌,顶部岩体呈悬空状,因此判断其可能成为危岩体。从现场调查来看岩体前端悬空导致其背后产生拉裂缝,因此其失稳模式为拉裂坠落式破坏。


图9 “驴羊图”岩画附近坠落式危岩体
1.计算方法
受到边界条件限制,该危岩体不宜采用静力解析法来计算稳定系数,而利用有限单元法来判断其是否稳定可能更加合理。本次分析使用的程序为ADINA(版本8.5.0),并将危岩体简化为两端固定、两端自由的矩形中厚悬臂板模型。考虑到缺少岩石三轴试验结果,因此无法得到岩石内摩擦角和黏聚力,故模型只能是采用各向同性线弹性的假设,并将其划分为500个3-DSolid单元。
2.计算荷载
计算荷载包括危岩体重力以及水平地震力。按照建筑抗震设计规范(GB50011-2010)附录A的规定,银川地区抗震设防烈度为8度,设计基本地震加速度值为0.20克,因此水平地震力的影响系数取为0.20。
3.计算参数
计算参数是否妥当对于计算结果至关重要。在各向同性线弹性的模型中需要输入的计算参数为岩石密度、泊松比和岩体变形模量。此外为了比较岩体受力状况,还需要知道岩体单轴抗拉强度。岩石泊松比取为0.3,密度为2.7克/米3,对于岩体变形模量和单轴抗拉强度则可以通过计算求得。根据现场统计,岩体体积节理Jv,裂隙表面轻微风化,于是查表可知:GSI=50,mi=19。由于对参数D尚缺乏系统的研究,在本文中暂取为0.4(还需进一步探讨其合理性)。将其代入式①②和③可得σmt=-158kPa(负号表示拉应力)和Erm=3.2GPa。
4.判断标准
严格来讲,有限单元法的计算结果并不是精确的,但是它能够反映各项状态的变化趋势。由于本文采用线弹性模型,所以只考虑弹性位移和应力的变化(见图16—图18)。由结果可知,危岩体最大位移仅为2.17×10-6米,并且在大部分范围内x和y方向的应力都小于岩体单轴抗拉强度,表明该危岩体整体处于稳定状态。但是在边界区域应力则超过了岩体单轴抗拉强度,说明该区域可能产生裂隙,因此还需采取其他模型进行细入研究。
(三)“手印图”岩画
“手印图”岩画两侧存在多处倾倒式危岩体。
1.计算方法
岩体周围被一组裂隙切割,产状为115°/NE∠82°,裂隙顶部较宽,底部闭合,所形成的危岩体尺寸为3.5×0.7×0.5米(见图10)。在重力、地震力及裂隙水压力作用下危岩体将有沿底部向外倾倒的趋势,因此属于倾倒失稳模式。


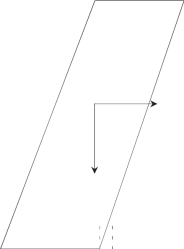
图10 倾倒式危岩体及其计算示意图
2.计算荷载
计算荷载包括危岩体重力、水平地震力以及暴雨状态的裂隙水压力。
3.计算参数
在倾倒式危岩体稳定性计算中,需要确定的参数除了式⑥中数据外,还需要知道岩体的单轴抗拉强度。
4.计算公式
对危岩体基座倾覆点建立力矩,稳定系数的定义为抗倾覆力矩与倾覆力矩之比,计算公式为:
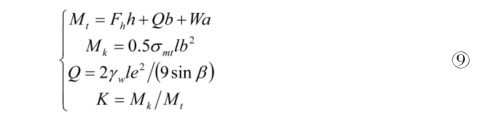
式中,Mt、Mk为倾覆力矩和抗倾覆力矩,Q为裂隙水压力(取暴雨状态),e为裂隙深度,σmt为岩体单轴抗拉强度,l为危岩体宽度。其余参数含义见⑥。此时e取为1.75米,α取为0.20米,计算可得k=0.94,表明该危岩体处于不稳定状态,应当采取锚杆等加固措施。
(四)“牧猎图”岩画
“牧猎图”岩画所处岩体具有上、下两部分临空面,临空面剖面坡度近直立(如图11—图18)。上段临空面高度约4米,宽度约3米,下段临空面高度约2米,宽度约3米。由于后期风化卸荷及雨水掏蚀等因素下,在上段岩体底部开始出现凹岩腔,尽管现在还不连续,但局部腔体较深。
在上段岩体顶部,发育一组平行于临空面的卸荷裂隙,其产状为走向305°,倾向35°,倾角近垂直。从顶部观察,该组卸荷裂隙形成明显的破碎带,破碎带厚度约1米。有的裂隙中生长了杂草,而东段岩体在重力作用下已经坍塌;从侧面来看,该组卸荷裂隙间距较窄,裂隙内部充填泥质碎块,裂隙最外侧距离临空面约200厘米。
此外,在上段岩体东侧还发育一条垂直于临空面的裂隙(限于条件,无法近距离对其观察)。从周围目测来看,该裂隙纵向切割深度有限,属于表层发育的风化裂隙,但需要注意必须防止其和岩体后部的卸荷裂隙贯通,形成新的危岩体。

图11 岩体东侧状况

图12 岩体整体概况

图13 岩体顶部状况

图14 岩体东侧坍塌部位

图15 岩体底部裂隙尺寸

图16 岩体侧面表层浅裂隙和剥蚀层

图17 上段岩体的底部凹岩腔

图18 上段岩体底部的风化剥蚀产物
1.裂隙产状调查
在“牧猎图”岩画底部发育多组裂隙,为了解岩体优势结构面产状和危岩稳定性分析,必须对其进行测量(如图19—图22)。如图通过测量,共发育四组裂隙,其产状分别为:①73°/NW∠16°;②45°/NW∠89°;③120°/NE∠83°;④38°/SE∠54°;
2.危岩体稳定性分析
根据现场调查,“牧猎图”顶部的危岩体的可能失稳模式为拉裂倾倒式失稳。因为危岩体底部存在空隙,坡面与裂隙之间在危岩体重力力矩的作用下继续张拉裂隙,危岩体将发生倾斜变形,从而可能折断危岩体本身或拉断岩桥段而倾倒失稳,进而危岩将先后沿其余裂隙以同样方式失稳。

图19 牧猎图底部裂隙岩体(南侧)

图20 牧猎图底部裂隙岩体(西侧)

图21 牧猎图底部裂隙岩体(东侧)

图22 牧猎图底部裂隙岩体(西南侧)
3.计算荷载组合
作用在危岩体上的荷载类型主要包括危岩体自重和主控结构面充水后产生的裂隙水压力及地震力。将上述计算荷载进行组合,可得到三种荷载组合类型:
组合一:自重。
组合二:自重+裂隙水压力。
组合三:自重+裂隙水压力+地震力。(https://www.daowen.com)
显然考虑组合三比其他组合更加严格(即安全系数更低),所以从保守角度考虑,本次分析仅考虑危岩体在荷载组合三时的安全系数。
4.安全系数
针对拉裂倾倒式失稳模式,可以通过不同的极限平衡力学模型进行安全系数计算。查阅现有文献,对此类危岩体稳定性计算可以有两种计算方法:
(1)材料力学计算公式。被深宽裂隙切割的长条形岩柱可以看作为顶端自由的悬臂梁,其失稳方式是自由端的累积挠曲位移而产生的根部折断或岩桥拉断。因此可以用材料力学中的惯性矩概念来推求危岩的倾倒失稳判据。
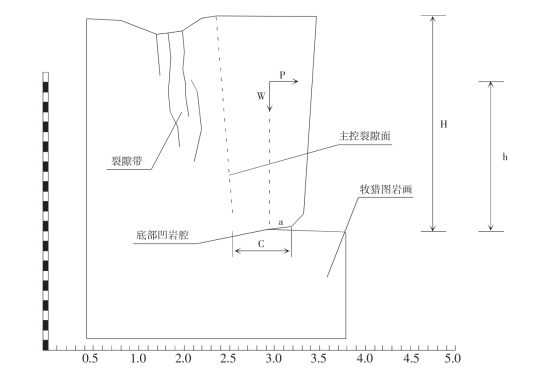
图23 牧猎图危岩体倾倒失稳计算简图
设在悬臂梁的固定端产生最大弯矩和最大拉应力分别用Mmax和σmax,当σmax大于岩体的抗拉强度σt时悬臂梁会倾倒折断而失稳,因此岩柱失稳的第一判据为:
![]()
当引入材料力学惯性矩概念,可得到如下公式:
![]()
令式輥輯訛等于1,得到裂隙临界宽度,该式可以作为岩体失稳的第二判据:
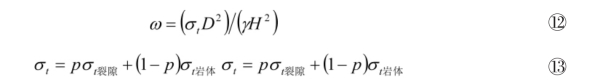
式中,γ为岩体重度,ω为倾倒危岩裂隙在地表的出露宽度,p为裂隙连通率,H为危岩高度,D为危岩底宽。其中最重要的便是确定岩体抗拉强度σt岩体和裂隙连通率p。
岩体抗拉强度σt岩体可以参考式②和④确定。本次设计中采用的参数为mt=19,Jv=5~7,GSI=60,D=0.4,于是可得 σt岩体=-349KPα。其余计算参数(见表 4)。代入式輥輯訛后可得 K=1.69。
表4 “牧猎图”安全系数计算参数

(2)力矩平衡计算公式。对危岩体基座倾覆点,倾覆力矩和抗倾覆力矩分别为:

式中公式的含义可以参考式⑨。设计中,取a=0.05米,e=2米,经过计算可得安全系数K=2.57。
(五)“太阳神”岩画
“太阳神”岩画是贺兰山地区最重要的岩画之一,因此对其进行研究显得尤为重要。
1.裂隙产状调查
通过现场调查,“太阳神”岩画周边共发育 5 组裂隙:①113°~127°/NE∠69°~80°;②152°/SW∠2°~5°;③233°/NW∠26°;④301°/NE∠60°;⑤220°/SE∠88°。其中第一组为层间裂隙,裂隙最为发育,张开度较大,对岩画稳定性影响也较大(见图24、图25)。

图24 “太阳神”岩画东侧道路旁裂隙

图25 “太阳神”岩画西侧道路旁裂隙

图26 “太阳神”岩画顶部裂隙

图27 “太阳神”岩画顶部裂隙
2.岩体稳定性分析
“太阳神”岩画所处位置为裂隙发育部位,如图26、图27。在其背后,恰好被一条卸荷裂隙切割(见图28),而在左右两侧各有一条倾斜裂隙将岩体破碎(见图29)。在岩画右侧,岩体呈现碎块状(见图30)。同时,由于长期风化作用,使得岩画底部空隙加大,有逐渐贯通的趋势(见图31)。“太阳神”岩画所在岩体为不规则形状。经测量,其最大尺寸约为110×156×18 厘米。

图28 “太阳神”岩画卸荷裂隙

图29 “太阳神”岩画两侧裂隙

图30 “太阳神”岩画右侧岩体破碎带

图31 “太阳神”岩画底部裂隙
岩体重心位于岩体外侧,故使用公式⑥。其中计算参数取为σmt=-158KPa,a=0.10米,e=0.55米,经计算可得该岩体的安全系数为2.1,属于稳定状态。
当然这只是简单的和初步的分析,有很多因素没有考虑,因此建议继续将强对岩画岩体的监测工作,同时采取更为准确的计算方法(例如数值模拟)分析岩体稳定性。
(六)“人面群像”岩画
“人面群像”岩画表面共发育两组裂隙:① 98°~116°/NE∠25°~38°;②51°/NW∠70°。该岩体属于块状结构,整体情况稳定,但仍需注意岩体表面节理,可能成为冻融发育的地方,从而造成岩画表面剥落和模糊,如图32和图33。

图32 “人面群像”岩画整体状况

图33 岩画底部表面节理
(七)“符号与人面像”岩画
“符号与人面像”岩画被两组裂隙切割,一组近乎水平,一组近垂直(见图34和图35)。从岩体结构角度而言,岩体属于块状结构,处于稳定状态。

图34 “符号与人面像”岩画整体状况

图35 岩体内部两组裂隙
(八)“岩画群”岩画
该处岩体被两组裂隙切割成块状,如图36和图37。其顶部岩体破碎,底部裂隙为主控结构面。由于被下部岩体遮挡,故其处于稳定状态。对岩画构成威胁的是其表面密集发育的一组浅裂隙,会造成岩体风化起壳和表面模糊。

图36 “岩画群”岩画状况

图37 切割岩体的裂隙

图38 “圣像壁”岩画岩体状况

图39 “圣像壁”岩画岩体的裂隙
(九)“圣像壁”岩画
“圣像壁”岩画西侧为岩体破碎带,主要存在一组裂隙,产状为240°/NW∠85°~90°。并且在岩画表面发育一组浅裂隙,造成岩体风化起壳和表面模糊。见图38、图39。
五、贺兰口危岩体加固设计
从现有分析结果来看,仅有一处危岩体处于不稳定状态,即位于“手印图”附近的第一组危岩体。
假设稳定系数,则可以由危岩体稳定系数的定义得到锚杆的抗倾覆力矩约为11.5KN。考虑到该组危岩体体积较小,且倾覆力矩也不大,因此可以采用单锚杆进行加固。
锚杆设计依据《建筑边坡工程技术规范》(GB50330-2002)执行。由于锚杆拉力设计值不大,故按照危岩体实际情况计算锚杆锚固段长度过小,所以根据相关规定以及类似工程经验,岩石锚杆的锚固段长度不应小于3米,且不宜大于45D(D为锚固体直径)和6.5米。
六、结论
在本次方案设计中,对贺兰口岩画地区的危岩体分部和稳定性状况做了初步研究,可以得到以下结论:
(1)贺兰口岩画地区分部大小不一、状态不同的危岩体。
(2)危岩体体积虽小,但是其附近或者表面存在岩画,因此也不容忽视。
(3)采用Hoek-Brown经验准则估算了贺兰口岩画部分地区的岩体抗拉强度。
(4)采用静力解析法对部分边界条件简单的危岩体稳定性进行了初步的分析。按照现有条件计算,大部分危岩体趋于稳定状态。
由于条件限制无法进行详细的地质调查和试验,因而得出的结论在以下方面还存在不足:
(1)本次设计方案主要针对贺兰口道路两侧的部分岩画保护,因此方案中涉及的危岩体不可能覆盖该地区的全部范围。
(2)部分危岩体位于山坡陡峭位置,给近距离观察和测量带来不便,故危岩体尺寸可能并不准确。
(3)岩体力学参数对于危岩体稳定性分析至关重要。尽管本次设计方案中采用了Hoek-Brown经验准则进行了估算,但是由于缺少详细地质勘测,尤其是现场试验,因此存在一定偏差。
(4)危岩体稳定性的分析方法有很多种,本次设计方案只选用了相对简单的静力解析法。其优点是可以较快速的对危岩体稳定性进行定性判断,但是对于边界条件相对复杂的危岩体则无能为力。
鉴于贺兰口地区岩画的重要性以及地质条件复杂性,建议在本次方案的基础上继续开展以下工作和研究:
(1)在贺兰口岩画地区进行详细地质调查,尤其注意对岩画本体及其附近的岩体地质条件的勘察。
(2)采取多种手段(例如三维扫描技术)准确测量危岩体尺寸,并在条件适宜时近距离测量危岩体周围裂隙产状、填充状况以及尺寸。
(3)在不影响岩画保护的前提下,增加现场岩体力学测试,了解不同位置的岩体力学参数(例如岩体抗拉强度、内摩擦角、粘聚力等)。
(4)增加其他方法(例如现场物探和室内数值模拟等)对部分边界条件复杂的危岩体稳定性进行更细致的分析。
(5)对重点部位的岩画附近危岩体进行现场监测,以确保文物和游客的安全。
