9.7.6　二叉树查找算法

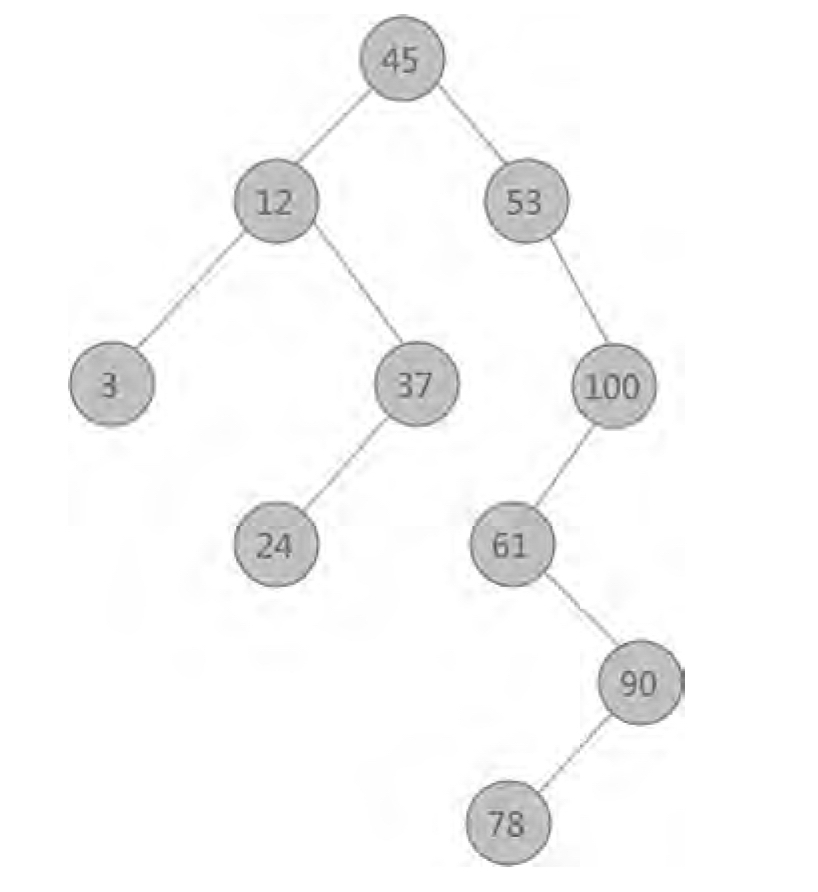
二叉树查找算法是最简单的树表查找算法。先对待查找的数据进行生成树，确保树的左分支的值小于右分支的值，然后在就和每个节点的父节点比较大小，查找最适合的范围。这个算法的查找效率很高，但是如果使用这种查找方法要首先创建树。

二叉查找树（BinarySearch Tree，也叫二叉搜索树，或称二叉排序树Binary Sort Tree），具有下列性质的二叉树：

·若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；

·若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；

·任意节点的左、右子树也分别为二叉查找树。

二叉查找树性质：对二叉查找树进行中序遍历，即可得到有序的数列，如图9-49所示。

图9-49　二叉查找树

使用二叉排序树实现动态查找操作的过程，实际上就是从二叉排序树的根节点到查找元素节点的过程，所以时间复杂度同被查找元素所在的树的深度（层次数）有关。最好情况下，二叉树是完全平衡的，此时查找和插入的时间复杂度都为O（log n）。最坏情况下，二叉树呈线型，此时查找和插入的时间复杂度都为O（n）。平均情况下，时间复杂度为O（log n）。

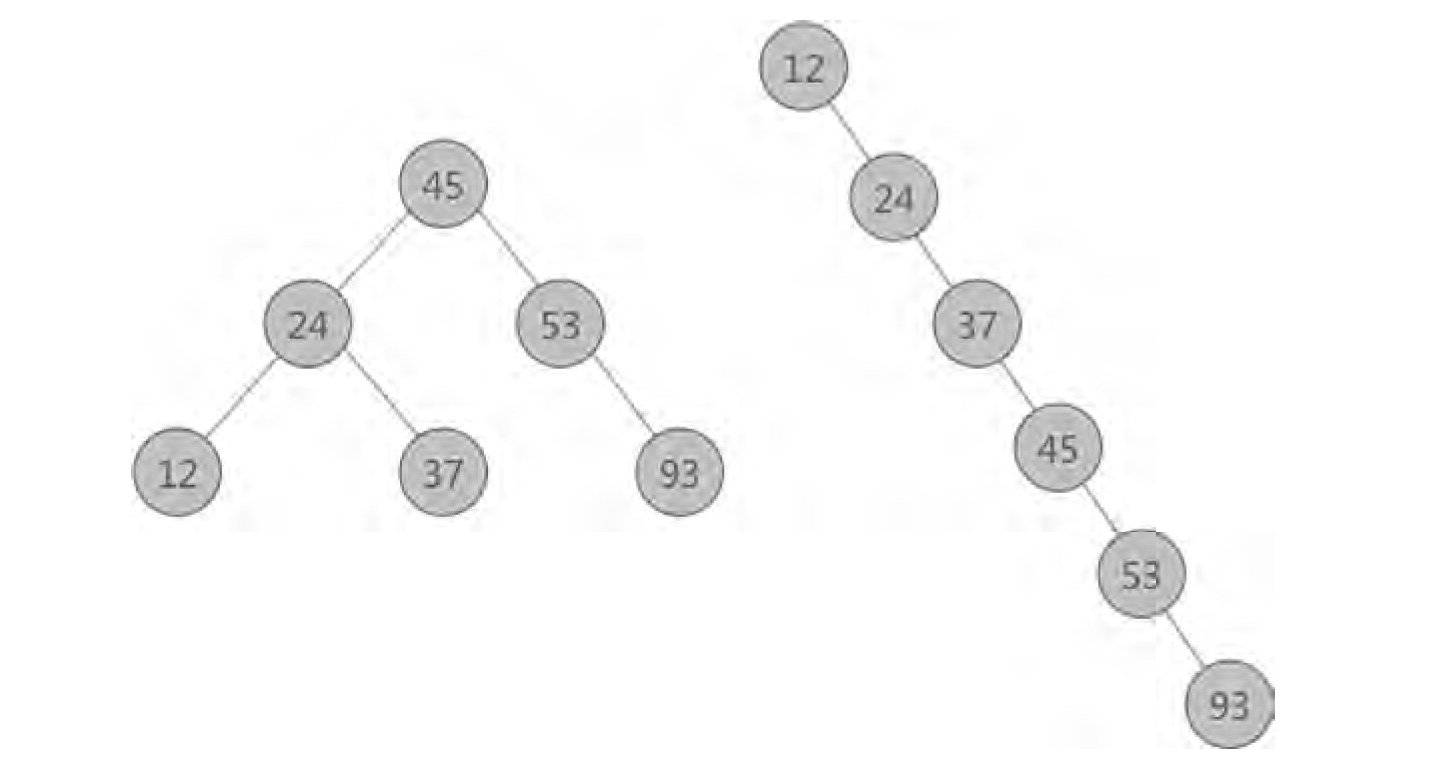
为了弥补二叉排序树构造时产生如图9-50所示的影响算法效率的因素，需要对二叉排序树做“平衡化”处理，使其成为一棵平衡二叉树。

图9-50　二叉查找树的“平衡化”