3.3.2 欧洲微放电检测标准
欧洲的微放电检测标准由ESA的标准化机构ECSS主导编写,已经发布的标准主要有2003年发布的ECSS-E-20-01A,2013年的修订版ECSS-E-20-01A Rev.1及2020年的ECSS-E-HB-20-01A和ECSSST-20-01C等标准。最新的微放电标准手册描述了射频组件与设备的设计测试指南及建议,以实现在空间运行中不发生微放电,它包括之前版本的内容,并且增加了二次电子发射测量研究成果;该标准涵盖了所有类别的卫星射频器件和设备在所有频段上发生的微放电特性。本节主要介绍与中国检测标准不同的部分:微波部件类型与微放电考核方法、微放电设计分析、多载波测试方法,二次电子发射测量相关研究进展在本书第2章2.3节做了相关介绍,其他内容具体参见参考文献[1][2][3]。
3.3.2.1 微波部件类型与微放电考核方法
微波部件表面材料的二次电子发射特性对微放电产生有重要影响。由于微波部件在加工、存储和运输过程中不可避免地存在污染,并会使用黏结剂和润滑剂等,使得微波部件微放电阈值降低,因此微波部件必须保证足够的微放电值余量。微放电设计余量是指微波部件的微放电阈值功率理论计算结果与额定工作功率之间的差额。在透气孔合理设计的条件下,ESA微放电设计与测试标准按照不同的微波部件类型规定了分析、鉴定级试验、抽检试验、单件产品试验四个阶段的微放电阈值考核余量。
在ESA微放电设计与测试标准中将微波部件分为三类:第一类(P1)是微波路径全为金属,或者是为增加微放电阈值而开展的非有机表面微处理的金属,并且金属的二次电子发射特性已知,微波部件透气孔设计合理;第二类(P2)为微波路径包含微放电特性明确的介质或其他材料,微波部件透气孔设计合理;第三类(P3)为除了前两类以外的其他类型微波部件。
对P1微波部件,在微放电阈值分析余量大于8 dB时,如果还满足以下三个条件,则可以不进行微放电试验,认为微放电考核通过:
(1)所分析微波部件是继承于与其类似的已经被验证的合格设计;
(2)所分析微波部件的结构能够进行准确、可靠的电磁场分析;
(3)成熟设计结构,其分析阈值和测试阈值建立了准确联系,所分析微波部件的微放电关键区域与该已有设计一致。
在微放电阈值分析余量不大于8 dB时,需要进行鉴定级微放电试验:测试阈值如果大于6 dB余量,则微放电考核通过;如果鉴定级微放电试验不满足6 dB余量,则需要针对飞行件进行微放电试验。如果是多件飞行件产品同批次投产,只进行微放电抽检;如果所抽样品的微放电阈值余量大于4 dB,则该批次飞行件微放电考核通过;如果抽检样品的微放电余量不满足4 dB或者为单件飞行件,则必须对每件飞行件进行微放电试验,要求微放电阈值余量大于3 dB方可通过微放电考核。
同时,ESA微放电标准中对P2和P3微波部件在不同阶段的微放电阈值考核余量进行了规定。P2微波部件的分析、鉴定级试验、抽检试验、单件产品试验四个阶段的微放电阈值余量分别为10 dB、6 dB、4 dB、3 dB;P3微波部件的分析、鉴定级试验、抽检试验、单件产品试验四个阶段的微放电阈值余量分别为12 dB、10 dB、6 dB、4 dB。P1、P2和P3微波部件的不同阶段单载波微放电阈值考核余量要求如表3-1所示。
表3-1 微波部件不同阶段单载波微放电阈值考核余量
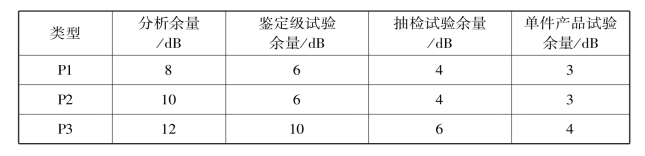
表3-1中微放电考核余量是建立在材料二次电子发射特性稳定的成熟工艺基础上的。如果工艺稳定性缺乏严格控制,即使在产品鉴定试验时微波部件满足了微放电阈值余量要求,但是对于新加工的正样产品仍然需要开展微放电测试试验,通常要求鉴定级的微放电测试余量不小于6 dB,同时飞行试验件微放电阈值余量不小于3 dB,并且对于鉴定件和飞行件都要进行微放电试验。针对三类微波部件单载波微放电考核流程如图3-2所示。
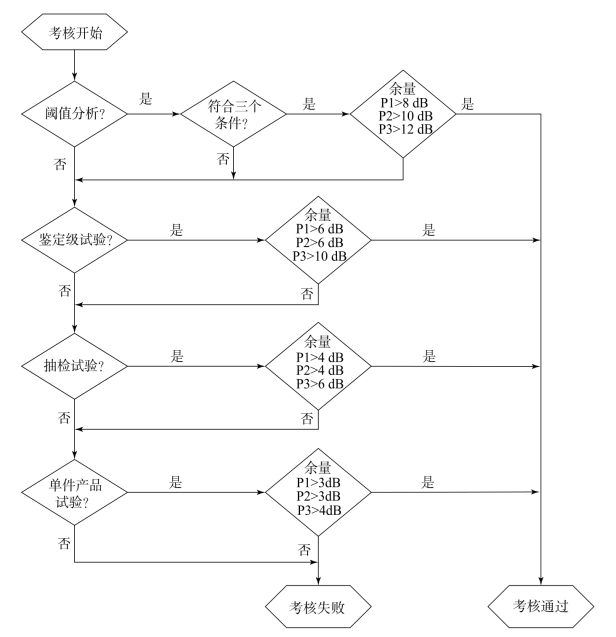
图3-2 微波部件微放电考核流程图
前面已经介绍了微波部件类型与微放电的考核相关内容,下面将对微波部件类型进行介绍。P1微波部件已开展过大量研究工作,新版的ESA标准中对P2和P3微波部件进一步开展了分析和研究。
1.P2部件介质充电效应
对于填充介质的微波部件而言,充电效应会使介质带电并在原射频电场的基础上叠加一个静电场,部件的尺寸以及电场变化都有可能对微放电过程造成影响。此外,介质充电的微放电敏感特性也与其处理方式有关,如加工工艺、静电摩擦、烘烤等。介质充电效应使电子倍增过程发生变化,且规律不具有普适性,因此在分析和测试中微放电阈值存在不确定性,所以目前的分析并没有充分考虑充电效应带来的影响。一般情况下,充电效应意味着发生微放电的可能性增加,尽管原电荷在介质表面分布并不均匀,而且通常是未知的,但数值分析可以在一定程度模拟其变化过程。此外介质的SEY特性也可能受到充电效应影响,导致其测试结果的不一致,最终影响整个分析的准确性。因为电介质的不确定性,在大功率条件下测试结果之间的差异也较为明显。以图3-3所示的同轴滤波器为例,表3-2列出了在图3-3所示的同轴滤波器中ESA采用不同介质材料替换介质板时仿真模拟微放电阈值和测试微放电阈值的差异。
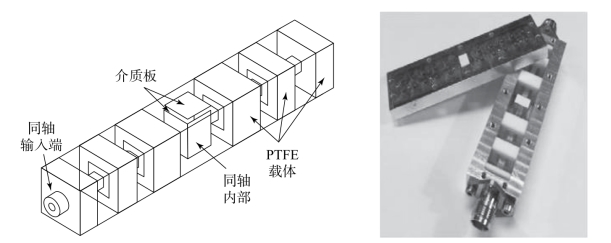
图3-3 同轴滤波器
表3-2 不同介质材料在同轴滤波器内的微放电模拟及测试对比
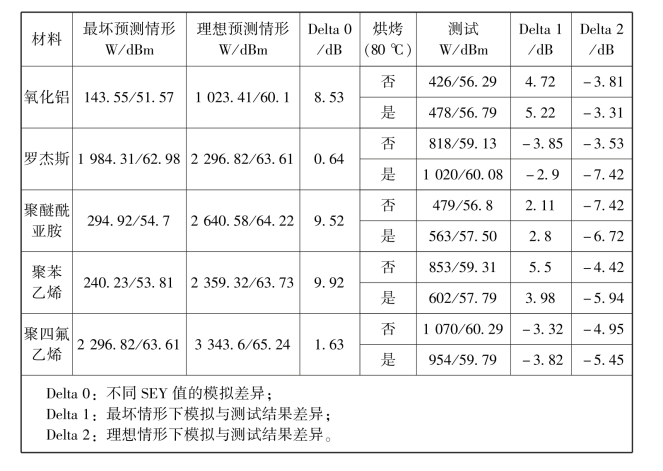
表3-2中阈值分析的SEY数据是通过不同的测试结果获得的,如图3-4所示,其中最坏的阈值分析所考虑样本SEY偏大,理想的阈值分析所考虑SEY较小。
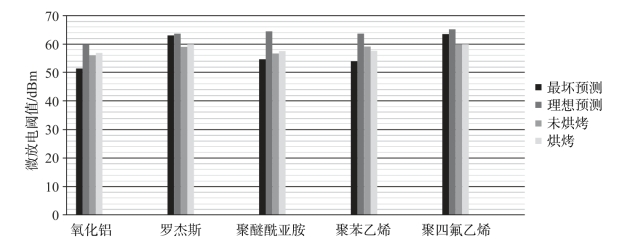
图3-4 不同介质材料在微波部件内的微放电模拟及测试对比(见彩插)
影响阈值产生差异的因素除了微放电效应外,还包括局部释气引发的电晕放电,或三点效应。J.Puech等人研究了不同电导率的介质建模精度,对于相对高电导率的介质,发现用“类金属”方法测量和预测的结果有较好的一致性,但对于电导率较低的介质,其测试和预测结果差异较大。M.Belhaj等进行了不同条件下的充电测试,可借此区分介质电导率的相对高低。
2.与P2和P3部件相关的其他放电类型
在航天器微波部件内存在电介质的情况下(对于P2和P3型部件),可能会出现静电放电现象,并将其统称为“三点效应”,所谓“三点”指三种媒质,即在一个区域内同时存在金属、介质和真空接触条件,并且金属与介质和/或真空间存在尖锐边界接触(见图3-5)。当临界射频场在金属边缘区域达到一定强度时,会激发电子的场发射现象。部分自由电子及金属所激发的电子受到静电场的作用朝着电介质相对带正电的区域运动。当介质二次电子的发射系数最大值σmax大于1时,介质表面更容易带正电,这增加了静电场和场发射的能力,若电场的作用范围没有边界,二次电子会在电场的影响下逐渐远离表面。随着电流密度的增加,雪崩过程仅受到金属锐边或尖端熔化的限制。然而,一旦熔化过程完成,射频电场振幅降低,则“三点”现象趋于消失。
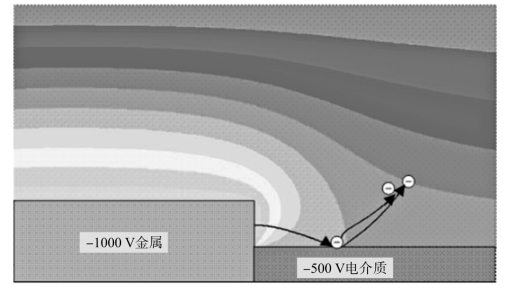
图3-5 反向电压梯度配置中三点放电示意图(见彩插)
(电位轮廓用色标表示,金属出射的电子会被吸引到邻近的电介质区域,若二次电子的发射系数大于1,两者的电位差会更大)
3.3.2.2 微放电设计分析
微放电的两个关键影响因素:一是f×d,二是临界间隙电压随频率的变化。随着f×d的增大,发生微放电的概率变大。在某些情况下,更高的频率意味着更强的场,可以抵消f×d的增加,得到更低的微放电阈值,这意味着至少需要在频段内的三个频率点进行电磁场分析,即在中心频率和上边频、下边频分别研究。为了更好地研究微放电现象,需要明确部件内电场的变化,通过电磁软件或等效电路建模分析其部件内的电场变化,而且部件内所有不同间隙区域的电压变化都需要考虑,尤其在窄间隙高压结构处。微放电分析分为理论分析与三维数值射频电磁计算软件分析。
1.理论分析
最基础的微放电分析模型是基于两个无限延伸的平行板结构,然而,大多数真实的射频器件的几何结构内部是不均匀的射频电场和弯曲的场线。在这种情况下,基于平行平板结构击穿阈值的往往过于保守,一般采用含有膜片的波导来做微放电优化设计,由于膜片是一个常用的波导管部分,可以实现匹配的目的,应用在滤波器中,又可以耦合不同腔体中的不同电磁模式。
现有的理论只适用于含有膜片结构的矩形波导,基于这些理论并对电子损失机制进行建模,推导出有效的SEY模型,并与经典平行板微放电理论一起计算微放电阈值。
(1)横向扩散导致的电子损失:R.Udiljak等人研究了基于膜片与平行板结构的二维模型,并讨论了发射电子非零切向速度而导致的电子损失机制,其中电子沿膜片结构切线方向的传输问题,是通过统计学方法中一维随机传输过程来模拟的。为实现微放电模拟,二次电子的生成速率要高于电子的损耗速率。因此,通过对电子损失速率的近似计算,有效二次电子发射率可(σeff)定义为:
![]()
它总是低于材料和平行板理论所给出的标称SEY(σ)。γ0的值由扩散公式近似地表示为:
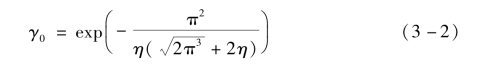
其中η为:

式中,vt是切向二次电子发射速率的平均值,l是膜片长度,d是间隙大小,f是射频频率,N是微放电模式阶数。 (注:η与d/l的值直接相关,这与试验结果一致)。
(2)边缘场造成的电子损失:V.E.Semenov等人对电容式膜片进行二维建模,并采用共形技术对静态场进行分析,通过这种方式,电场可以沿着膜片的切线方向进行计算。研究发现,膜片中心区域的电场可以近似为平行平板结构的电场,结合相关SEY数据并考虑横向随机发射速度和边缘场,便可采用分析平行板方法类比计算膜片结构的微放电电压。
(3)Sombrin和Hatch及Williams图表:经典的Sombrin图、Hatch和Williams的微放电敏感图被广泛应用于测试研究中,以对比不同条件下所得到的不同微放电阈值。(https://www.daowen.com)
在使用这些经典的微放电理论时,通常使用连接不同阶数微放电阈值的包络线代替精确的微放电区域,如图3-6所示。这是因为在经典理论中,不同微放电阶数之间存在着较大的差异,这可能导致非保守预测。不幸的是,传统的Sombrin和Hatch以及Williams的曲线,若不与试验数据进行拟合,就只能精确匹配一阶微放电的试验结果,其余微放电电压都发生了变化。除此之外,谐振区域过窄,即使插入偶数模也不会产生微放电。
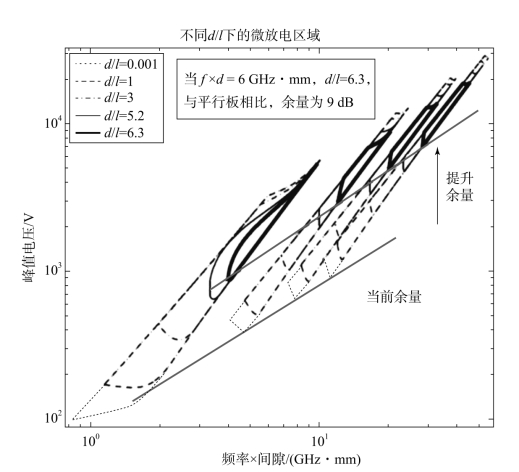
图3-6 典型二维Sombrin图(不同d/l比率的边缘场效应对比)(见彩插)
(4)非稳态理论的应用:该理论包含了电子发射速度的随机性,能够精确计算所有微放电阶数下的击穿阈值,并通过结合相关的SEY数据可以计算微放电的敏感区域,如图3-7所示。
2.三维数值射频电磁计算软件分析
三维数值射频电磁计算软件,除了考虑部件结构内的电磁场变化,还可以模拟粒子在电磁场中的运动轨迹,并自动纳入边缘场效应。这是一种合理准确的方法,可以预测不同情况下的微放电。该标准中常用的微放电仿真分析工具有FEST3D/SPARK3D、CST Particle Studio等仿真软件(见图3-8),目前已被法国达索(DASSAULT,DS)公司收购。
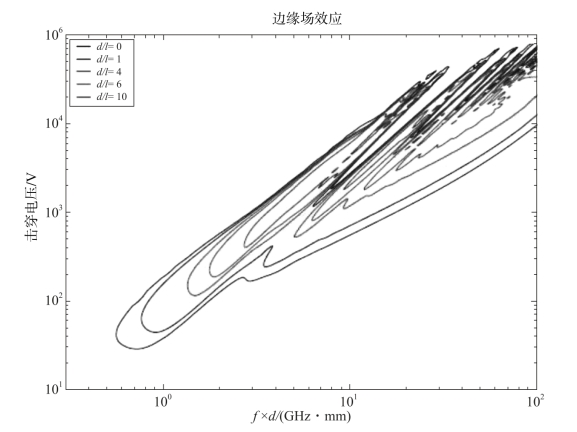
图3-7 不同的d/l下带有边缘场效应的非稳态理论微放电计算(见彩插)
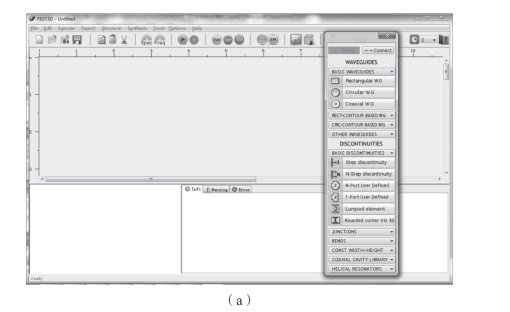
图3-8 常用的微放电仿真分析工具
(a)FEST3D
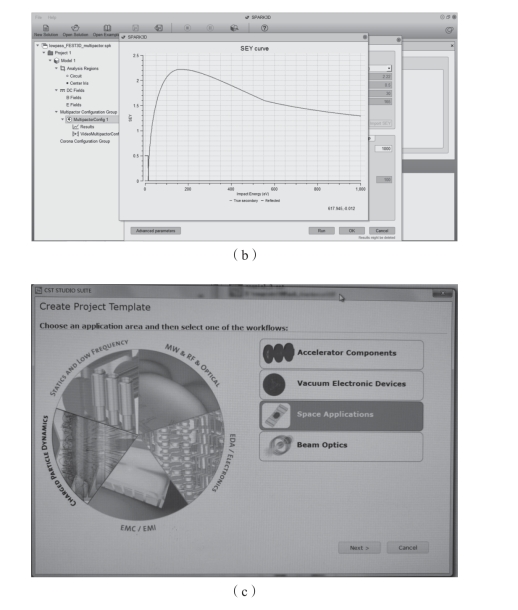
图3-8 常用的微放电仿真分析工具(续)
(b)SPARK3D;(c)CST Particle Studio
3.3.2.3 多载波测试方法
1.用等效功率下的单载波进行多频测试
通过定义合理的等效单载波(又称连续波,Continuous Wave,CW),就可使用CW测试类比研究多载波放电问题。多载波信号在时域上可以近似为时间为t on和振幅为V on的脉冲信号。可以确定最差情况下产生的最低微放电阈值电压V mc(V on,t on),如图3-9所示。
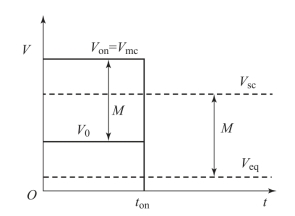
图3-9 脉冲模型和CW的余量定义
图3-9中各参数的含义为:t on为最差情况下的脉冲持续时间,V on为多载波信号在t on时间内的微放电阈值,V0为多载波工作电压,V eq为等效单载波电压,V sc为单载波电压阈值,M为工作电压和多载波阈值之间的余量。
等效单载波电压是指在单载波中的应用电压V eq,它相对于单载波电压阈值V sc产生相同的余量M。

功率形式表达为:

式中,P eq,sc为等效的CW功率,P th,sc为单载波阈值,P0为多载波平均运行功率(所有载波功率值之和),P th,mc为多载波平均阈值(所有载波功率值之和)。
为了计算等效的CW功率,需要同时进行单载波和多载波分析。
理论上,多载波功率阈值由以下因素制约:

这对等效CW功率提出约束条件:
![]()
根据式(3-6),等效定义一个替代式(3-8)的方法:

最后总结出下面的边界定义:
若Pth,sc<P th,mc,Peq,sc=P0;若P th,sc>NP th,mc,Peq,sc=NP0;若Pth,mc≤P th,sc≤NP th,mc,用式(3-6)。
可以借助图3-3所示同轴滤波器进行说明,分析结果是单载波阈值P th,sc=1 421W,通过数值分析得到的多载波阈值P th,mc=8载波×181 W/载波=1 448 W,每个载波的平均运行功率P0=8载波×45 W/载波=360W。
方法1:等效的CW功率P eq,sc=353 W,因为该值低于式(3-8)中的P0,因此产生的等效CW功率P eq,sc=360W。
方法2:不等式(3-10)没有得到满足,因此P eq,sc=360W,按此标准对之后的余量提出要求,余量为6 dB。
2.用较少载波数的等效功率进行多载波测试
在载波数量减少的情况下,等效情况可以描述如下:
![]()
余量定义为:

其中m是载波数量,n是减少的载波数。用式(3-6)定义一个使用m及n载波的等效CW单载波功率,由于两种情况下的等效CW功率必须是相等的,因此可使用式(3-6)将两种方式结合起来。
经过验证,式(3-12)与式(3-11)结果相同。
