2.5.1 数学课程本体构建
数学学科分支较多。比如,数学二级学科包括基础数学、计算数学、应用数学、概率论与数理统计以及运筹学与控制论。数学课程通常具有概念多、符号多以及关联性强等特点。Gruber提出的本体构建原则包括清晰性和客观性、一致性、最大单调可扩展性、最小编码偏见以及最小本体承诺[21]。基于数学类课程特点和数学课程本体的相关工作,采用如下数学课程本体构建准则[22,23]:
(1)层次性。构建数学本体需要区分不同数学课程的共同概念化知识和特定具体课程的独有知识。为此,引入数学课程上层本体和数学课程内容本体。构建数学本体需要区分数学课程的概念知识与数学习题的概念知识。为此,引入数学课程习题本体。
(2)完整性。数学课程上层本体应尽可能囊括所有数学课程对象及其性质和关系。数学课程内容本体应尽可能包括特定课程的知识点、课程目标、学习对象的特性及其关系。数学课程习题本体应尽可能包括面向不同课程、不同知识点的概念层面的习题特点和性质。
(3)开放性。对于新增课程和知识,数学本体易于更新和扩充到现有本体中,独立于数学本体表示语言。
定义(数学课程上层本体):数学课程上层本体包括概念类、运算类、属性类、关系类、断言类、实例类。其中,关系类={上下位关系,部分-整体关系,实例关系,依赖关系,因果关系,约束关系,先修关系,对义关系,概念与属性关系,概念与性质关系,属性与属性值关系}。
例如,离散数学课程中的“有向图”隶属于概念类,“有向图和基图之间的关系”和“零图和平凡图之间的关系”则隶属于关系类[24]。
由于数学课程中的数学对象种类繁杂,并且具有符号化、抽象化和形式化等特点。因此,构建数学课程上层本体的难点在于应尽可能囊括不同课程的概念类别以及概念层的数学对象关系。本节所述数学课程上层本体的特点是:
(1)将概念类、运算类、属性类、关系类、断言类、实例类构建为同一概念层次。数学课程上层本体明确了各数学课程对象隶属于概念类、运算类、属性类、关系类、断言类或实例类。根据课程的特点可以动态增加新的概念类别,使得不同概念类别不包括相同的数学对象实例。
(2)定义关系类的内涵,包括上下位关系、部分-整体关系、实例关系、依赖关系、因果关系、约束关系、先修关系、对义关系、概念与属性关系、概念与性质关系、属性与属性值关系。数学课程主要研究数学对象包括数量关系和空间形式两大类。数学概念是数学知识的基础要素,分析数学概念的关系是数学知识的核心要素。
定义(数学课程内容本体):数学课程内容本体是一个六元组(C,Op,A,V,R,As),其中,C为概念集合,Op为运算集合,A为属性集合,V为属性值集合,R为关系集合,As为断言集合。由这六个本体构成要素构成数学课程知识。
例如,图2.5给出了离散数学课程内容本体中图论的概念体系。该概念体系包括数学课程上层本体的上下位关系。在图2.5中,三元组“(无向简单图,上下位关系,正则图)”成立,表示无向简单图是正则图的上位概念。三元组“(森林,上下位关系,无向树)”成立,表示森林是无向树的上位概念。需要指出的是,图2.5中若上位概念按照同一分类依据划分下位概念的话,则划分的所有下位概念的外延集合交集是空集。例如,按照是否存在方向可将图划分为无向图和有向图,按照对点和边是否指定符号可将图划分为标定图和非标定图。
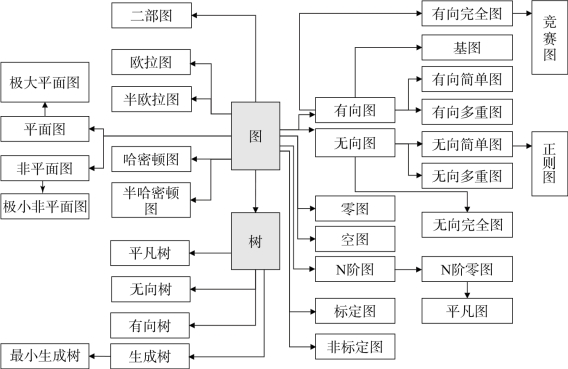
图2.5 离散数学课程内容本体中图论的概念体系
仍以离散数学为例进行分析。离散数学课程的图论本体中,例如,对于欧拉图,三元组(欧拉图,充要条件,无向连通图没有奇数度顶点)成立,其含义是欧拉图的充要条件是无向连通图没有奇数度顶点。对于树,三元组(树,边数,顶点数减1),其含义是树的边数等于其顶点数减1。
定义(数学课程习题本体):数学课程习题本体是一个六元组(Ce,Tp,Ys,Ge,Me,Ps),其中,Ce为习题内容集合,Tp为习题题型集合,Ys为习题类型集合,Ge为习题所考察的本体构成要素及其关系,Me为习题求解方法集合,Ps为习题求解过程集合。
其中,习题题型集合Tp为{填空题,判断题,选择题,证明题,计算题,问答题,应用题,作图题,阅读题}。习题求解方法集合Me为习题解答的各种方法。习题求解过程集合Ps包括习题解答的各种过程。习题类型集合包括六大类,即概念关系习题类型、概念实例关系习题类型、实例关系习题类型、概念属性习题类型、实例运算习题类型、概念和实例断言习题类型。例如:
(a)“(概念c1,?关系,概念c2)”属于概念关系习题类型,表示求解概念c1和c2存在哪些关系。
(b)“(?概念,关系r,实例i)”属于概念实例关系习题类型,表示求解哪些概念与实例i存在关系r。
(c)“(实例i1,!关系r,实例i2)”属于实例关系习题类型,表示判断实例i1和实例i2是否存在关系r。
(d)“(概念c1,属性a,?属性值)”属于实例关系习题类型,表示求解概念c1的属性a的属性值。
(e)“(实例i,运算o,?运算结果)”属于实例关系习题类型,表示求解实例i的运算o的运算结果。
(f)“(概念c1,!断言s)”属于实例关系习题类型,表示判断概念c1的断言s是否成立。
下面给出一个有关离散数学课程习题本体的示例。例如,对于习题“请问完全图K5是平面图吗?”,该习题题型为判断题,该习题类型为(概念c1,上下位关系,实例i1),即(平面图,上下位关系,完全图K5)。该习题所考察的本体构成要素及其关系为(平面图,上下位关系,完全图)。该习题的求解习题方法为反证法,利用欧拉公式进行证明完全图K5不是平面图。其求解习题过程为,若完全图K5是平面图,则由于完全图K5中无环和平行边,所以每个面的次数均大于等于3,由欧拉公式的推广定理可知,完全图K5的边数应该满足式子10≤3(5-2)/(3-2)=9,产生矛盾。因此完全图K5是非平面图。
