8.2.2 属性知识验证
8.2.2.1 单种属性关系的属性知识验证
本节阐述如何验证涉及一种属性关系的实体属性值的一致性和完备性。表8.1给出了实体属性值的错误类型及其验证方法。
表8.1 不同类型的错误及其验证方法
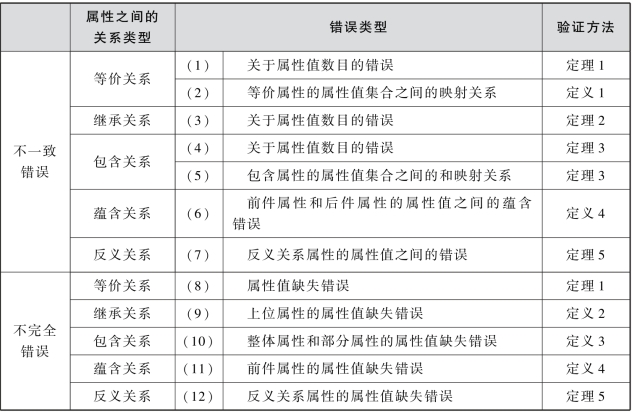
定理1.对于概念c,及其两个属性a1和a2,若AttEquivalent(c,a1,a2)成立,则公式(8.6)为真。其中,EqualNumber(V1,V2)是指集合V1与集合V2的元素个数相同。
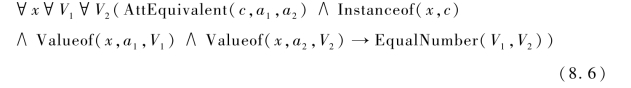
证明:根据定义1,从集合V1到V2存在一一映射或双射f。因此,能够获得公式EqualNumber(V1,V2)为真。
对于等价属性a1和a2,若它们的属性值满足定理1和定义1,则可以判断等价属性a1和a2不存在表8.1中错误(1),(2)和(8)。具体地,
a)当公式EqualNumber(V1,V2)不成立时,则属性a1和a2会产生不一致错误(1)“关于属性值数目的错误”。
b)当集合V1到V2不存在一一映射或双射f时,则属性a1和a2会产生不一致错误(2)“等价属性的属性值集合之间的映射关系”。
c)当公式EqualNumber(V1,V2)不成立时,即集合V1或集合V2存在缺失属性值时,则属性a1和a2会产生不完全错误(8)“属性值缺失错误”。
定理2.对于概念c,及其两个属性a1和a2,若AttInherit(c,a1,a2)成立,则公式(8.7)为真。其中NotGreaterNumber(V1,V2)是指集合V1的元素个数不大于集合V2的元素个数。
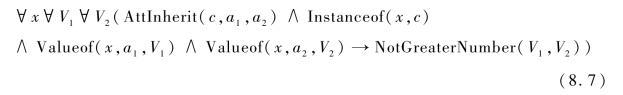
证明:根据定义2,可以推断,对于集合V1中的任意元素v,在集合V2中至少存在一个元素与元素v相同或等价。因此,可以推断出:集合V1中的元素个数小于或等于集合V1中的元素个数。
对于具有继承关系的属性a1和a2,如果它们的属性值满足定理2,则避免产生表8.1中的错误(3)和(9)。具体地,
(a)当NotGreaterNumber(V1,V2)不成立时,会产生错误(3)“关于属性值数目的错误”。
(b)当存在集合V1中的元素v,对于集合V2中的任意元素w,元素w与元素v不相同或不等价。
定理3.对于概念c及其两个属性a1和a2,若AttInclude(c,a1,a2)成立,则公式(8.8)为真,并且从集合V1到集合V2存在一对多的包含关系映射。
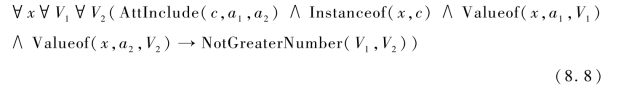
证明:根据定义3,对于集合V2中的任意元素v,集合V1中至少存在一个元素包含v;对于集合V1中的任意元素w,集合V2中至少存在一个元素被元素w包含。另外,由于集合V1中的属性值不具有相同部分,这些属性值包含集合V2中的不同元素。因此,从集合V1到集合V2存在一对多的映射。进一步,NotGreaterNumber(V1,V2)成立。
若属性a1包含属a2,若它们的属性值满足定理3和定义3,则不会产生表8.1中错误(4),(5)和(10)。
(a)当NotGreaterNumber(V1,V2)不成立时,会产生错误(4)“关于属性值数目的错误”。
(b)当从集合V1到集合V2不存在一对多的映射时,会产生错误(5)“包含属性的属性值集合之间的和映射关系”。
(c)当属性a2存在一个属性值v,属性值v没有被属性a1的任一属性值所包含,反之亦然,则会产生错误(10)“整体属性和部分属性的属性值缺失错误”。
定理4.对于概念c及其两个属性a1和a2,若AttImply(c,a1,a2)成立,则公式(8.9)为真,其中,NonNull(V)表示集合V是非空集合。
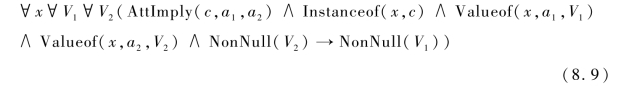
证明:对于集合V2中任一元素v,根据定义4,集合V1中至少存在一个元素蕴含元素v。因此,如果集合V2是非空集合,则集合V1也是非空集合。
若属性a1蕴含属性a2,若它们的属性值满足定理4和定义4,则不会产生表8.1种错误(6)和(11)。(https://www.daowen.com)
(a)当属性a2的属性值错误的话,会产生表8.1中错误(6)“前件属性和后件属性的属性值之间的蕴含错误”。
(b)当公式NonNull(V2)∧﹁NonNull(V1)不成立时,会产生表8.1中错误(11)“前件属性的属性值缺失错误”。
定理5.对于概念c,及其两个属性a1和a2,若AttAntonymous(c,a1,a2)成立,则公式(8.10)为真。
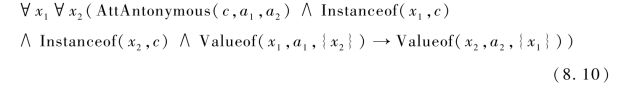
证明:根据已知条件,可以推断出:Valueof(x1,a1,{x2})为真。因此,如果Valueof(x1,a1,V)为真,则x2属于V。进一步,根据定义5,推断出Valueof(x2,a2,{x1})成立。
对于具有对义关系的两个属性,若这两个属性的属性值满足定理5,则能够避免产生表8.1中的错误(7)和(12)。
a)当公式Valueof(x1,a1,{x2})∧﹁Valueof(x2,a2,{x1})成立时,会产生表8.1中错误(7)“反义关系属性的属性值之间的错误”。
b)若存在实体x1的属性a1的属性值v,v的属性a2的属性值集合不包含x1,则产生表8.1中错误(12)“反义关系属性的属性值缺失错误”。
8.2.2.2 多种属性关系的属性知识验证
本节讨论如何验证实体属性涉及概念属性之间的多种关系的属性值。
定理6.对于概念c,及其任意四个属性a1,a2,a3和a4,对于具有等价关系和继承关系的属性,公式(8.11)和(8.12)成立。
类似地,对于具有等价关系和包含关系的属性,公式(8.13)和(8.14)成立。
对于具有等价关系和蕴含关系的属性,公式(8.15)和(8.16)成立。
对于具有等价关系和对义关系的属性,公式(8.17)和(8.18)成立。

证明:对于概念c的实例x,设实例x的属性a1,a2和a3的属性值集合分别为V1,V2和V3。对于属性值集合V2中任意元素v,由于AttEquivalent(c,a1,a2)为真,所以,属性值集合V1中存在元素u等于或等价于元素v。进一步,AttInherit(c,a1,a3)为真,因此,属性值集合V3中存在元素w等于或等价于元素u。对于属性值集合V2中任意元素v,属性值集合V3中存在元素w等于或等价于元素v。根据定义2,推断出公式AttInherit(c,a2,a3)为真。公式(8.12)和其他公式均可以采用类似方法进行证明。
对于具有等价关系和继承关系的多个属性,当知识AttInherit(c,a2,a3)或AttInherit(c,a1,a4)不存在知识库中时,会产生不完全错误“继承关系缺失”。若满足定理6,则可以避免产生该错误。其他不一致错误和不完全错误如同表8.1中的错误(3)和(9)。对于具有等价关系和包含关系的属性、等价关系和蕴含关系的属性、等价关系和对义关系的属性,可以采用类似的错误和错误检测方法。
定理7.对于概念c,及其任意三个属性a1,a2和a3,若这三个属性之间具有继承和包含关系,则公式(8.19)和(8.20)成立。

证明:对于概念c的实例x,设实例x的属性a1,a2和a3的属性值集合分别为V1,V2和V3。对于属性值集合V3中任意元素w,由于AttInherit(c,a3,a2)成立,所以,属性值集合V2中至少存在一个元素v相同于或等价于w。进一步,AttInclude(c,a1,a2)成立,因此,属性值集合V1中至少存在一个元素u包含w。根据定义3,可以推断出:AttInclude(c,a1,a3)为真。公式(8.20)可以采用类似的方法证明。
定理8.对于概念c,及其任意三个属性a1,a2和a3,若这三个属性之间具有继承和蕴含关系,则公式(8.21)和(8.22)成立。进一步,若这三个属性之间具有包含和蕴含关系,则公式(8.23)和(8.24)成立。

证明:对于属性值集合V3中任意元素w,由于AttImply(c,a2,a3)成立,所以属性值集合V2中至少存在一个元素v蕴含元素w。进一步,AttInherit(c,a2,a1)为真,属性值集合V1中至少存在一个元素u相同于或等价于v。因此,对于属性值集合V3中任意元素w,属性值集合V1中至少存在一个元素u蕴含w。根据定义,可以推断出:AttImply(c,a1,a3)成立。公式(8.22),(8.23)和(8.24)可以采用类似的方法进行证明。
对于具有继承和包含关系的多个属性,若在知识库中不存在知识AttInclude(c,a1,a3),则会产生不完全错误“包含关系缺失”。若满足定理7,则不会产生该错误。其他不一致和不完全错误类似于表1中错误(4),(5)和(10)。对于具有继承关系和蕴含关系的属性,包含关系和蕴含关系的属性,具有类似的错误和错误检测方法。对于具有继承关系、包含关系和蕴含关系的属性,根据定理8可以推断出性质定理9。
定理9.对于概念c,及其任意三个属性a1,a2和a3,若a1,a2和a3之间具有继承关系和包含关系,则公式(8.25)和(8.26)成立。
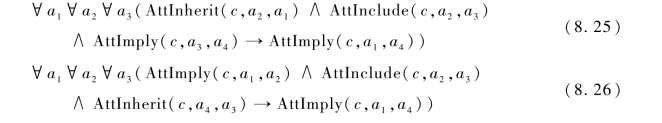
对于具有继承关系、包含关系和蕴含关系的属性,当知识AttImply(c,a1,a4)不存在于知识库时,会产生不完全错误“蕴含关系缺失”。当满足定理9时,该错误不会产生。其它错误类似于表8.1中错误(6)和(11)。
