7.2 描述流定性分析和定量分析
下面分析描述流的性质。
性质5.1:若描述子d1≼d2,{d11,d12,…,d1m}⊆d1,{d21,d22,…,d2n}⊆d2,m,n为整数,则d1i≼d2j(i=1,2,…,m,j=1,2,…,n)。
证明:若d1≼d2,d1i⊆d1,则d1i≼d2。又d2j⊆d2,则d1i≼d2j。
该性质表明:对于满足描述偏序关系的两个描述子,它们的孩子保持该序关系。依此推广,可以得到性质5.2。
性质5.2:若描述子d1≼d2≼...≼dn-1≼dn,d1={d11,d12,…,d1m1},d2={d21,d22,…,d2m2},…,dn={dn1,dn2,…,dnmn},m1,m2,…,mn为整数,则d1i1≼d2i2≼...≼dn-1in-1≼dnin(i1=1,2,…,m1,i2=1,2,…,m2;…,in=1,2,…,mn)。
下面给出描述流的定性分析。描述流可以分为必要描述流和可选描述流。进一步,可选描述流可以分为主描述流和辅描述流。
定义(必要描述流):给定语料Ct,设Ct包含n篇文本,其中,n为正整数。如果每篇文本均采用描述流DS的叙述方式,则描述流DS称为相对于该语料的必要描述流。
定义(可选描述流):给定语料Ct,设Ct包含n篇文本,其中,n为正整数。如果存在k(k〈n)篇文本采用描述流DS的叙述方式,其中,k为正整数,则描述流DS称为相对于该语料的可选描述流。
定义(主描述流、辅描述流):给定语料Ct,设Ct包含n篇文本,其中,n为正整数。如果存在k(k/m≥α)篇文本采用描述流DS的叙述方式,其中,k为正整数,α为阈值,则描述流DS称为相对于该语料的α-主描述流,否则称为相对于该语料的α-辅描述流。
下面给出描述流的定量分析。描述流按照其相似性可分为三类:相同描述流、相似描述流和相异描述流。
定义(相同描述流):给定两个描述流DS1=〈D1,⊆,≼>和DS2=〈D2,⊆,≼>,如果
(1)D1=D2;
(2)描述子的包含关系结构和偏序结构均相同;
则将DS1和DS2称为相同描述流。也就是,这两个描述流的描述子以及描述子的序关系均完全相同。
定义(相异描述流):给定两个描述流DS1=〈D1,⊆,≼>和DS2=〈D2,⊆,≼>,如果D1∩D2=∅,则将DS1和DS2称为相异描述流。也就是,这两个描述流不含有相同的描述子。(https://www.daowen.com)
定义(弱相似描述流):给定两个描述流DS1=〈D1,⊆,≼>和DS2=〈D2,⊆,≼>,如果D1∩D2≠∅,则将DS1和DS2称为弱相似描述流。也就是,这两个描述流含有相同的描述子。
定义(强相似描述流):给定两个描述流DS1=〈D1,⊆,≼>和DS2=〈D2,⊆,≼>,如果
(1)CD=D1∩D2≠∅;
(2)∀d1i1,d1i2,d2j1,d2i2∈CD,若d1i1,d1i2∈D1,d2j1,d2j2∈D2,d1i1=d2j1,d1i2=d2j2,d1i1≼d1i2,则d2j1≼d2j2。
则将DS1和DS2称为强相似描述流。也就是,这两个描述流含有相同的描述子并且描述子的序关系均完全相同。
定义(描述子的路径段):给定描述流DS=〈D,⊆,≼>,设di,dj∈D,将结点di到结点dj的由出现关系决定的路径称为描述子di到描述子dj的路径段,记作Path(di,dj)。
定义(描述子距离,Descriptor Distance):给定结构描述流DS=〈D,⊆,≼>,设di,dj∈D,定义描述子di和dj的距离为:|Path(di,dj)|。
性质5:给定线性结构描述流DS=〈D,⊆,≼>,设di,dj∈D,di≼dj,描述子di和dj的距离为:DD(dj-di)=j-i。
证明:因为di,dj∈D,所以DD(dj-di)=|Path(di,dj)|=j-i>0.
定义(描述子对距离,Descriptor Pair Distance):给定两个线性结构描述流DS1=〈D1,⊆,≼>和DS2=〈D2,⊆,≼>,设d1i1=d2j1,d1i2=d2j2,...,d1in=d2jn,n为正整数,定义相同描述子对〈d1ik,d2jk>和〈d1ik-1,d2jk-1>的距离为:
DPD(〈d1ik-1,d2jk-1>,〈d1ik,d2jk>)=DD(d1ik-d1ik-1)-DD(d2jk-d2jk-1)。
定义(偏移距离,Excursion Distance):给定两个线性结构描述流DS1=〈D1,⊆,≼>和DS2=〈D2,⊆,≼>,它们的偏移距离定义为:
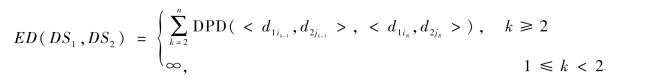
其中,d1i1=d2j1,d1i2=d2j2,…,d1in=d2jn,n为正整数。
