3.3.4 时辰表示和转换
对于农历日中小时表示方法,常用的三种表示方法包括,基于天色的表示方法、基于地支的表示方法以及基于更点制的表示方法。中国古人将一个农历日平均分为十二个时间段,每个时间段称为一个时辰。十二时辰按照顺序构成集合{夜半、鸡鸣、平旦、日出、食时、隅中、日中、日昳、晡时、日入、黄昏、人定}。
十二时辰名称的含义与日出日落的自然规律、天空颜色的变化和人们的生活习惯紧密相关。例如,人定是指人静的时候,即人们停止活动,安歇睡眠,具体指21点至23点这段时间。给出一个关于时辰人定的公理,其中函数shi-chenFn(t)表示t所在的时辰,SCs是十二时辰的集合。
a)(sc=shi-chenFn(t)∧sc=Ren-ding)
↔(startFn(sc)=9:00pm)∧(endFn(sc)=11:00pm)
b)∀sc((sc∈SCs)∧durationFn(sc,hour)=2))
地支也可用来表示时辰。每个时辰对应一个固定的地支。例如,时辰人定也称为亥时,其地支为亥。十二时辰名称依次为:子时、丑时、寅时、卯时、辰时、巳时、午时、未时、申时、酉时、戌时、亥时。例如,关于时辰人定的公理如下所示。
(shi-chenFn(t)=Ren-ding)↔terrestrial-branch-no(t,shi-chen,2)。
公历计时系统中的小时也可以由干支系统表示。时辰的天干是由时辰所隶属的农历日的天干计算出来的。具体地,可按公理TCT12进行转换:
TCT12.∀m∀n(terrestrial-branch-no(t,shi-chen,m)
∧celestial-stem-no(t,lunar day,n)→celestial-stem-no(t,shi-chen,modFn(2×modFn(n,5)-1,10)+modFn(m-1,10)))
其中,m,n是自然数。
例如,设t为2022年10月1日时辰丑时,计算该时间点丑时的干支组合表示的步骤如下:
a)2022年10月1日的干支组合表示是丁亥,celestial-stem-no(October 1.2022,lunar day,24)为真。
b)由于t在时辰丑时,所以terrestrial-branch-no(t,shi-chen,2)为真。
c)基于TCT12,有
celestial-stem-no(t,shi-chen,modFn(2×modFn(n,5)-1,10)+modFn(m-1,10))
=celestial-stem-no(t,shi-chen,modFn(2×modFn(1,5)-1,10)+mod-Fn(2-1,10))
=celestial-stem-no(t,shi-chen,2).
d)由于第二个天干为乙,因此2022年10月1日丑时干支组合表示时辰乙丑。(https://www.daowen.com)
基于更点制的小时计时方法将农历日晚上7:00至次日凌晨5:00划分为连续的五个子区间:一更、二更、三更、四更和五更。例如,给出关于二更和三更的公理,其中函数gengFn(t)表示t所在的“更”。
(g=gengFn(t)∧g=ER-geng)↔(startFn(g)=9:00pm)∧(endFn(g)=11:00pm)
(g=gengFn(t)∧g=San-geng)↔(startFn(g)=11:00pm)∧(endFn(g)=1:00am)
从十二个时辰可以看出,一更、二更、三更、四更和五更分别对应戌时辰、亥时辰、子时辰、丑时辰、寅时辰。
∀g∀sc((g=Er-geng)∧(sc=Hai-shi)→equal(g,sc))
∀g∀sc((g=San-geng)∧(sc=Zi-shi)→equal(g,sc))
下面阐述时间实体的组合表示。在汉语口语和书面语中,许多时间表达式采用多种方法来表示同一个时间实体,称为组合式表示方法。例如,对于壬寅虎年,该农历年(The Lunar Year of Ren-yin and TigerRat)使用两种农历年的表示方法,包括干支系统和生肖表示方法。
下面将讨论不同时间段的各种组合表示,即农历年、农历月、农历日和小时。根据三种农历年的表示方法,即基于干支系统、十二生肖系统、以及皇帝封号或年号的农历年表示方法,可以构成不同的组合表示方式。农历年组合表示的组成部分主要包括:朝代名称、皇帝的封号、皇帝的名字、皇帝的年号、农历年的序数、农历年的干支组合表示、农历年的地支表示、农历年的生肖表示。例如,组合表示的一个例子是“唐朝肃宗至德三年”。它包括a)统治朝代名称:唐朝;b)皇帝的封号:肃宗;c)皇帝年号:至德;d)农历年的序数:农历第三年。该时间点所对应的公历年是公元758年。
农历月的组合表示包括两部分。第一部分是由农历年组合表示中的其中一种方法所表示的农历年。第二部分则是由两种农历月表示中的一种方法所表示的农历月。例如,清宣宗三年四月,对应的公历月是1823年5月,包含a)皇帝的帝号,即宣宗;b)农历年的序数,即第三年;c)农历月的序数,即第四个农历月。
对于农历日的组合表示也包括两部分。其中,第一部分是农历年的组合表示中的一种方法所表示的农历年;第二部分是由农历月和农历日的组合表示中的一种方法所表示的农历月和农历日。例如,“庚子年五月望日”是第三种组合表示的例子,包括:a)农历年的干支组合:庚子;b)农历年的序数:农历第五月;c)当天的月相:望日。其所对应的公历日是2020年7月5日和其他日期。
时辰的组合表示包括三部分。第一部分是农历年的组合表示中的一种方法所表示的农历年;第二部分是农历月和农历日的组合表示中的一种方法所表示的农历月和农历日;第三部分是时辰的三种表示中的一种方法所表示的时辰。例如,“清宣宗三年二月初一人定时”是指1823年3月13日晚上9:00到晚上11:00。它包括:a)皇帝的帝号:宣宗;b)农历年序数:农历第三年;c)农历月序数:农历月第二个月;d)农历日:初一;e)时辰天色表示:人定。
下面阐述时间实体转换的完备性。在公历计时系统构建中,建立公历计时单位(年、月、日、时)和农历计时单位(年、月、日、时辰)之间的转换关系是必要的。一个基础性问题是:给定公历计时系统中时间实体与中国传统计时系统中时间实体,是否存在相关计算方法可以实现二者之间的转换。这一任务的核心是构建公历计时系统中时间实体和农历计时系统中时间实体的映射关系。
图3.4给出了由不同表示方法所表示的时间实体之间的转换关系。图3.4上半部分给出了中国传统计时系统中,基于不同表示方法的时间段年的时间实体。图3.4下半部分给出了公历计时系统中时间段年的时间实体。从基于干支系统表示的农历年集合LS1到基于序数表示的公历年集合GS2之间存在一对多映射的转换关系,并且从集合GS2到集合LS1存在满射的转换关系。从基于序数表示的公历年到基于干支系统表示的农历年之间能够进行转换。
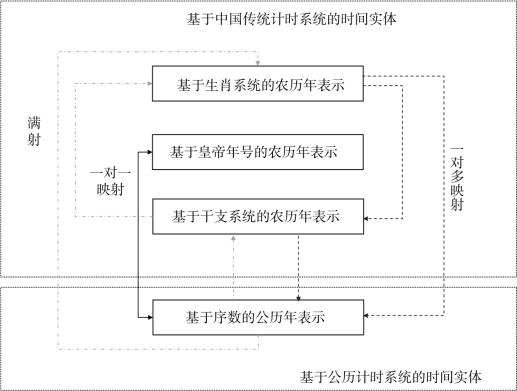
图3.4 基于不同时间表示方法的时间实体的转换关系
在基于地支系统表示的时辰集合和基于序数表示的小时集合中,存在一一映射的转换关系。再如,从基于月相表示的农历日集合到基于序数表示的农历日集合,存在单射转换关系。从基于干支表示的农历月集合S3到基于序数表示的农历月集合S4,存在一对多映射关系,并且从集合S4到集合S3存在满射关系。
需要注意的是,既没有精确的计算方法或公式来进行公历月和农历月之间的转换,也没有方法来进行公历日和农历日之间的映射或转换。月亮和太阳的变异和转动是不均匀的、不稳定的、摇摆不定的。因此,一个节气的长度并不总是大于一个农历月的长度,一个农历月可能包含两个主要的节气。
这里需要强调两点。首先,公历中的新年并不总是与中国春节重合,因此公历年和农历年的映射只是近似的。第二点是基于干支系统的农历年表示方法是从西汉开始的,所以后来人们推演出在西汉之前的农历年的干支组合表示方法。
