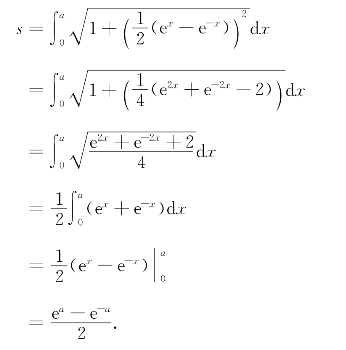参考答案 习题解答
参考答案 习题解答
第1讲
习题1—1 （i）解：y′＝4－4x；
（ii）解：y′＝
；
（iii）解：f′（x）＝
；
（iV）解：注意到（sin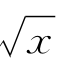
）2＋（cos
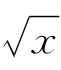）2＝1，得g′（x）＝3.
图象读者可用超级画板软件来作，此处略.
习题1—2 解：当|h|较小时有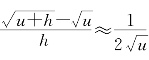
；取u＝4和h＝1得
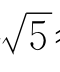≈2.25.
第2讲
习题2—1 解：g（x）＝
＝－1，当x∈（0，4]时，g（x）≥0，而当x∈（0，4）时g（x）＞0，故f（x）在（0，4]递增；类似可知f（x）在[4，＋∞）递减.（参看习题2－8）
习题2—2 （i）解：－7＋4x；
（ii）解：
；
（iii）解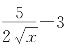
；
（iV）解：注意2cos2x－cos2x＝1，可知
是所给函数的乙函数.
习题2—3 解：计算f（x）＝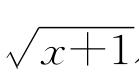
在两数u＜v（－1≤u）处的差商得
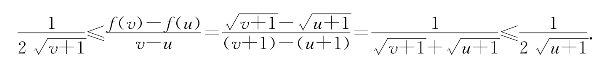
可见g（x）＝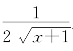
是f（x）＝
在（－1，＋∞）上的乙函数.
习题2—4 解：当－1＜u＜v时有
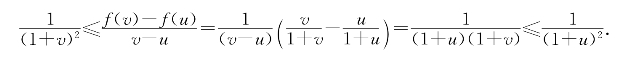
可见g（x）＝
是f（x）＝
在（－1，＋∞）上的乙函数.
当u＜v＜－1时有
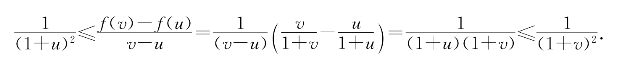
可见g（x）＝
也是f（x）＝
在（－∞，－1）上的乙函数.
习题2—5 解：在不等式（2－10）中取u＝10和
得到
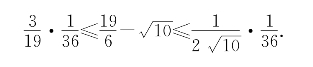
由此得到
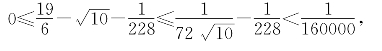
如果取
≈3.16228作为
的近似值，从不等式可知此近似值是过剩近似值，且误差不会超过0.000007.（实际上
＝3.16227766…）
习题2—6 解：对于任意两个自然数n＜m，有
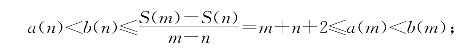
这表明a（n）和b（n）都是S（n）的乙函数.
习题2—7 解：对任意u＜v，若u·v≥0则显然有
＝sgn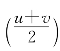
，结论成立.
若u·v＜0则有
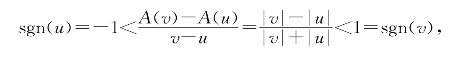
结论仍成立.
习题2—8 解：（i）从g（x）在（u，v）上恒为0，易知f（x）在（u，v）上为常数c.
用反证法，若f（u）＝d≠c，下面来推出矛盾.
取正数h使u＋h∈（u，v），由乙函数性质可知有[u，u＋h]上的点p和q使得
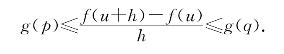
由于g（x）在[u，u＋h]上的值域为0或为g（u），故|g（q）－g（p）|≤|g（u）|，从而有
0＜|d－c|＝|f（u＋h）－f（u）|≤|g（q）－g（p）|·h≤|g（u）|·h，
这表明0＜|g（u）|.取h＜
推出2＜1，这否定了反证法假设，证明了f（u）＝c.类似可证f（v）＝c.
（ii）从g（x）在（u，v）上恒为常数k≠0，易知f（x）在（u，v）上为一次函数k·x＋C.用反证法，若（k·u＋C）－f（u）＝A≠0，下面来推出矛盾.
取正数h使u＋h∈（u，v），由乙函数性质可知有[u，u＋h]上的点p和q使得
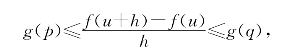
由于g（x）在[u，u＋h]上的值域为k或为g（u），故|g（q）－g（p）|≤|g（u）－k|，从而有
|A＋k·h|＝|f（u＋h）－f（u）|≤|g（q）－g（p）|·h≤|g（u）－k|·h，
这表明0＜|A|≤（|g（u）|＋2|k|）h.取h＜ 
推出2＜1，这否定了反证法假设，证明了f（u）＝k·u＋C.同理可证f（v）＝k·v＋C.
（iii）从g（x）在（u，v）上恒为正，易知f（x）在（u，v）上递增.用反证法，若有点z∈（u，v）使得f（u）－f（z）＝d＞0，下面来推出矛盾.
取正数h使u＋h∈（u，z），由乙函数性质可知有[u，u＋h]上的点p和q使得
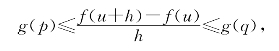
由于f（x）在（u，v）上递增，故有
g（p）h≤f（u＋h）－f（u）＜f（z）－f（u）＝－d＜0，
从而g（p）＜0，故p＝u.取h＜
推出－0.5＜－1，这否定了反证法假设.下略.
（iV）与前款类似，从略.
第3讲
习题3—1 解：考虑函数f（x）＝1＋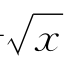
，
取u＝9，v＝9＋h，P＝（u，f（u））＝（9，4），
Q＝（v，f（v））＝（9＋h，1＋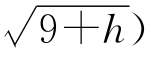
计算差商
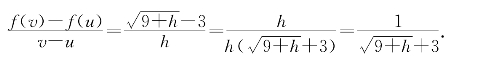
当v趋向于u时，即h趋向于0时，上式右端趋向于
.因此曲线在点P（9，4）处的切线斜率为
，切线方程为x－6y＋15＝0.
习题3—2 解：函数y＝
＋x的导数为y′＝
＋1.切点（u，v）处切线的斜率为
，故有
，解得u＝1，v＝
.
习题3—3 解：函数y＝
的导数为y′＝1－
.
切点（3，2）处切线的斜率为
，
直线x＋ay＋1＝0的斜率为
，由垂直条件得
＝－1，故a＝
.
习题3—4 解：函数f（x）＝9x－48＋66的导数为f′（x）＝9－
设切点的横坐标为u，则过点R（6，0）的切线方程应为
＝f′（u）＝9－
整理得
化简后得u－5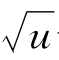
＋6＝0，解得u1＝4和u2＝9，对应切点P＝（4，6）和Q＝（9，3）.计算出△PQR的面积为12.如图.
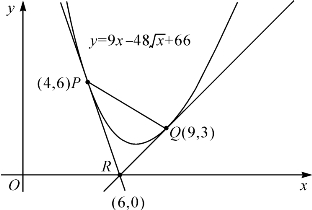
习题3－4的图
第4讲
习题4—1 解：计算给出
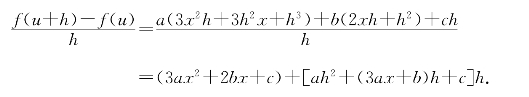
当h趋于0时右端趋于3ax2＋2bx＋c，它就是f（x）＝ax3＋bx2＋cx＋d的导数.
习题4—2 解：函数f（x）＝x3－12x＋8的乙函数是g（x）＝3x2－12，而g（x）在[－3，－2）和（2，3]上为正，在（－2，2）上为负；可见f（x）在[－3，－2]和[2，3]上递增，在[－2，2]上递减；故f（x）在x＝－2和x＝2分别取到极大f（－2）＝24和极小f（2）＝－8，而在区间两端有f（－3）＝17和f（3）＝－1，故函数f（x）＝x3－12x＋8在区间[－3，3]上的最大值与最小值分别为f（－2）＝24和f（2）＝－8.
习题4—3 解：函数f（x）＝t·x2＋2t2·x＋t－1的乙函数是g（x）＝2tx＋2t2，而g（x）在（－t，＋∞）上为正，在（－∞，－t）上为负；故f（x）在x＝－t取到最小值h（t）＝f（－t）＝t－t3－1.
易知h（t）＋t＝2t－t3－1的乙函数是2－3t2，它在（0，2）上递减，在
为正而在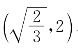
为负，故h（t）＋t在
处取到（0，2）上的最大值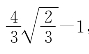
，在t＝2处取到[0，2]上的最小值－5，由此可得h（t）＋t在区间（0，2）上的取值范围是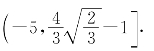
习题4—4 解：函数F（x）＝x－
的乙函数是g（x）＝
，由条件知g（x）在（－5，－1）上非负，故k≥－1；从而g（x）＝
在[1，3]上非负，故对固定的k得F（x）在[1，3]上的最大值为F（3）＝3－
，由k≥－1可得F（x）在[1，3]上的最大值为3－
.
习题4—5 解：函数f（x）＝
的乙函数是g（x）＝x2＋ax＋b，由条件知g（x）在区间[－1，1），（1，3]上各有一个零点.从而有
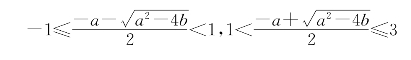
两式相加减得
容易检验当a＝－2且b＝－3时a2－4b取到最大值16，而f（x）有极值点x1＝－1和x2＝3.
习题4—6 解：函数f（x）＝2x3＋3ax2＋3bx＋8c的乙函数是g（x）＝6x2＋6ax＋3b，由条件知g（1）＝g（2）＝0，即6＋6a＋3b＝0且24＋12a＋3b＝0，解出a＝－3和b＝4.显然g（x）在[0，1）和（2，3]上为正，在（1，2）上为负，故f（x）在x＝1有极大值f（1）＝2＋3a＋3b＋8c＝5＋8c，在x＝2有极小值f（2）＝4＋8c，此外有f（0）＝8c和f（3）＝54＋27a＋9b＋8c＝9＋8c，故f（x）在[0，3]上的最大值为f（3）＝9＋8c，最小值为f（0）＝8c.
习题4—7 解：函数f（x）＝
的表达式在（－∞，＋∞）上有意义的充分必要条件是方程x2＋ax＋a＝0无实根，即a2＜4a，从而0＜a＜4.函数x2＋ax＋a在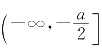
递减，在x＝－
取到最小，在
递增，故f（x）＝
的递减区间是.
习题4—8 解：设此内接圆柱体底半径为x而高为h，则
，故h＝30－3x，于是内接圆柱体的体积
V＝V（x）＝πx2h＝πx2（30－3x）＝3π（10x2－x3）.
求出V（x）＝3π（10x2－x3）的乙函数3π（20x－3x2），它有两个零点0和
，显然V（x）当x＝
时取到最大值V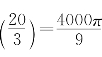 
.
第5讲
习题5—1 解：根据绝对值的性质，对任意[a，b]上的u和v有
|f（v）－f（u）|＝||v|－|u||≤|v－u|，
可见f（x）＝|x|在（－∞，＋∞）上差商有界，有一个李普西兹常数M＝1.
习题5—2 解：对任意[a，b]上的u和v有
|f（v）－f（u）|＝|v3－u3|＝|（v－u）（v2＋uv＋u2）|≤3（|a|＋|b|）2|v－u|，
可见f（x）＝x3在（－∞，＋∞）上差商有界，有[a，b]上的李普西兹常数M＝3（|a|＋|b|）2.
习题5—3 解：对任意不含0的[a，b]上的u和v，记m为|a|和|b|中较小者，则
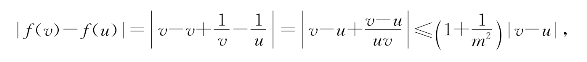
可见f（x）＝x＋
在（－∞，0）∪（0，＋∞）上差商有界，有[a，b]上的李普西兹常数M＝1＋
.
习题5—4 解：计算给出
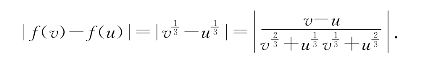
对任意的M＞0，在[0，1]上取u＝0和v＝（2M）－32，则
可见f（x）＝x1 3（x∈（－∞，＋∞））在（－∞，＋∞）上非差商有界.
另一方面，在不含0的[a，b]上，记m为|a|13和|b|13中较小者，则有
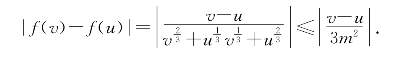
可见f（x）＝
在不含0的任意区间上差商有界.对0＜a＜b，它在[a，b]上显然有李普西兹常数
.
习题5—5 解：对任意[a，b]上的u和v，有
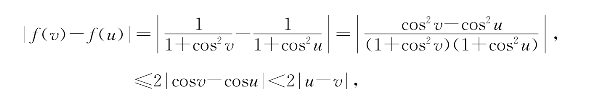
可见f（x）＝
在（－∞，＋∞）上差商有界.它在任意[a，b]上显然有李普西兹常数M＝2.
习题5—6 证明：对任意[a，b]上的u＜v，有
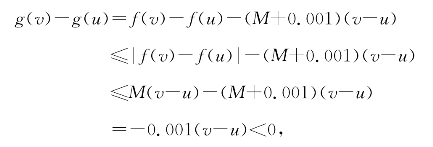
即函数g（x）＝f（x）－（M＋0.001）x在[a，b]上递减.
习题5—7 解：计算给出
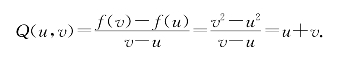
显然有2a＜Q（u，v）＜2b.
第6讲
习题6—1 解：在任意不含0的区间[a，b]上有
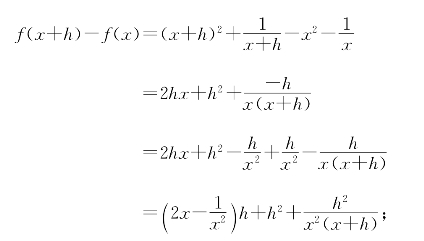
于是若以m记|a|和|b|中较小者，就有
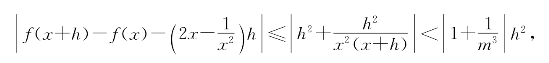
故得f′（x）＝2x－
.
习题6—2 解：当0＜u＜v时有
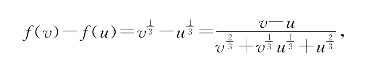
从而
，可见g（x）＝
是f（x）＝
的乙函数.
另一方面，对于任意0＜a≤u＜v≤b总有
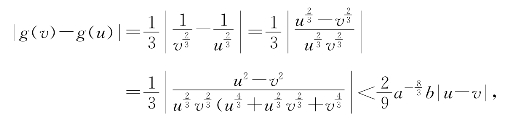
可见g（x）＝
差商有界，于是对x＞0有f′（x）＝g（x）＝
.
在x＜0时推导类似.
习题6—3 解：在任意区间[a，b]上有
F（x＋h）－F（x）＝（x＋h）4＋3（x＋h）3＋3（x＋h）2＋（x＋h）－（x4＋3x3＋3x2＋x）
＝（4x3h＋6x2h2＋4xh3＋h4）＋3（3x2h＋3xh2＋h3）＋3（2xh＋h2）＋h
＝（4x3＋9x2＋6x＋1）h＋（6x2＋4xh＋h2＋9x＋3h＋3）h2，
故有正数M＝|a|＋|b|＋1使得
|F（x＋h）－F（x）－（4x3＋9x2＋6x＋1）h|
＝|6x2＋4xh＋h2＋9x＋3h＋3|h2≤26M2h2.
可见有F′（x）＝4x3＋9x2＋6x＋1.
习题6—4 解：在任意区间[a，b]上的u＜v有
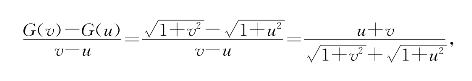
而u＜v时有
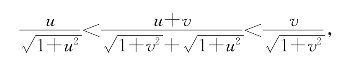
故g（x）＝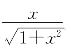
是G（x）＝
的乙函数；另一方面
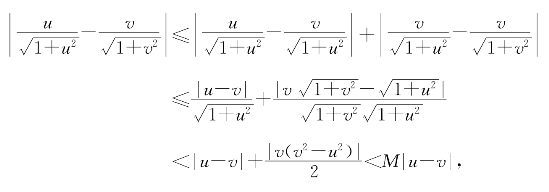
故有G′（x）＝
.
习题6—5 解：记m＝－n，对于u＜v，先计算出差商的一般表达式
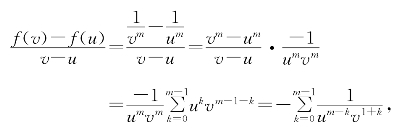
当u·v＞0时容易检验－
在
和
之间，故g（x）＝－mx－（m＋1）＝nxn－1在（0，＋∞）上和（－∞，0）上都是f（x）＝xn的乙函数.容易检验g（x）＝nxn－1在不含0的闭区间上的差商有界性，故得f′（x）＝g（x）＝nxn－1.
习题6—6 解：注意到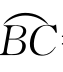
＝v－u＜tan（v－u）＝CH，则有
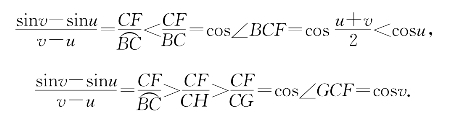
习题6—7 解：仿例题6－5，在（6－29）中取x＝45°＝
和h＝1°＝
≈0.017453，得到
误差不超过
≈0.0003.
第7讲
习题7—1 解：
（i）f′（x）＝100x99－20x3＋9x2－2x＋1；
（ii）f′（x）＝5x4（x10－x5＋1）＋（x5－1）（10x9－5x4）
＝5x4[x10－x5＋1＋（x5－1）（2x5－1）]
＝5x4（3x10－4x5＋2）；
（iii）f′（x）＝2xsinx＋x2cosx＋2cosx－2xsinx－2cosx＝x2cosx；
（iV）g′（x）＝[sin2（x2＋1）＋cos2（x2＋1）]′＝0；
（V）g′（x）＝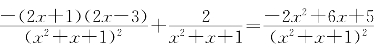
；
（Vi）f′（x）＝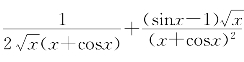
.
习题7—2 解：（f（x）g（x）h（x））′＝f′（x）（g（x）h（x））＋f（x）（g（x）h（x））′
＝f′（x）g（x）h（x）＋f（x）（g′（x）h（x）＋g（x）h′（x））
＝f′（x）g（x）h（x）＋f（x）g′（x）h（x）＋f（x）g（x）h′（x）.
习题7—3 解：将cotxtanx＝1两端求导得（cotx）′·tanx＋cotx·（tanx）′＝0，
即（cotx）′·tanx＋cotx·
＝0，
解出（cotx）′＝－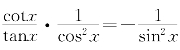
.
习题7—4 解：（i）2cos2x＝2cos2x－2sin2x；
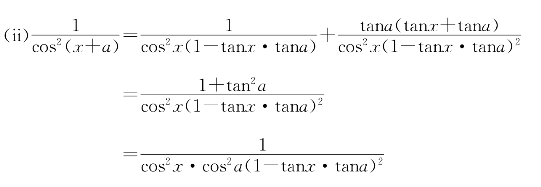
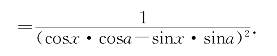
第8讲
习题8—1 解：（i）（（x2－3x＋7）33）′＝33（2x－3）（x2－3x＋7）32；
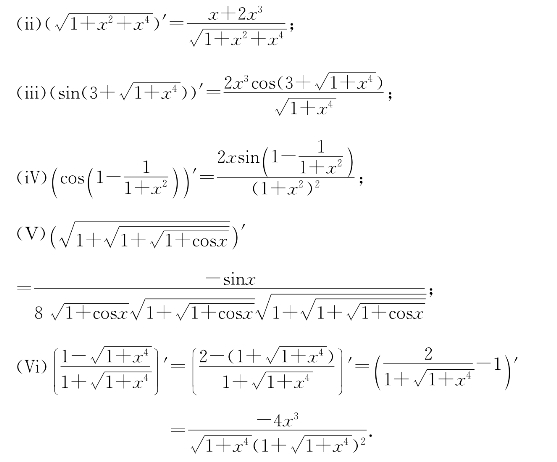
习题8—2 解：（H（G（F（ψ（x）））））′＝H′（G（F（ψ（x））））G′（F（ψ（x）））F′（ψ（x））ψ′（x）.
习题8—3 解：（i）对x2－xy－4y2＋y＝7求微分得
2xdx－xdy－ydx－8ydy＋dy＝0，
于是（2x－y）dx＋（1－x－8y）dy＝0，在点（3，－1）处有7dx＋6dy＝0，故此切线斜率为－
.
（ii）对x3＋xy－y3－2x2＝1两端微分得
3x2dx＋xdy＋ydx－3y2dy－4xdx＝0，
整理得
（3x2＋y－4x）dx＋（x－3y2）dy＝0，
于是曲线在点A处的切线斜率
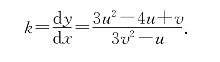
第9讲
习题9—1 证明：（i）根据自然对数基本性质，对任意0＜u＜v有不等式
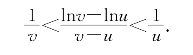
取v＝n＋1，u＝n即得所要的不等式；
（ii）由（i）得
＜ln（k＋1）－lnk＜
，对k＝1，2，…，n求和，即得所要的不等式；
（iii）由（ii）得
＜lnn＜
，
同减去
，得
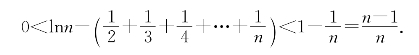
习题9—2 解：用一般对数定义，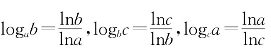
；
三者相乘等于1.
也可以设logab＝x，logbc＝y，logca＝z，
则ax＝b，by＝c，cz＝a；
于是a＝cz＝（by）z＝（（ax）y）z＝axyz，从而x·y·z＝1.
习题9—3 解：（i）（x2lnx）′＝2xlnx＋x；
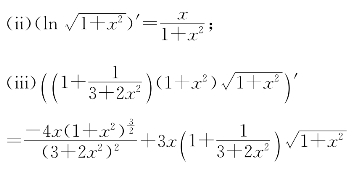
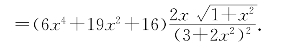
习题9—4 证明：已知对任意0＜u＜v有不等式
取u＝x，v－u＝h得
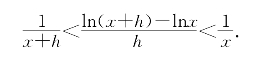
同乘h，再同减
得
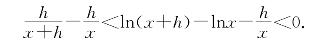
取绝对值可得
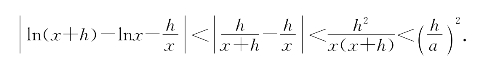
第10讲
习题10—1 解：（i）x2ex＋2xex；
习题10—2 解：（i）对cos（arccosx）＝x两端求导得－sin（arccosx）·（arccosx）′＝1，故
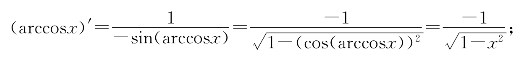
（ii）对cot（arccotx）＝x两端求导得－
＝1，故
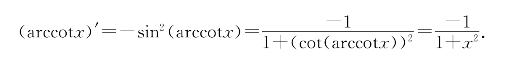
习题10—3 证明：当y＞x时，由不等式
取y＝x＋h得
从而0＜
，
即得|ex＋h－ex－hex|＜h2eb；
当y＜x时，
由不等式
＜ex取y＝x＋h得
从而
＜0，
用负数h乘后即得
得同样结论.
习题10—4 解：当a＝1时，函数y＝f（x）＝axlna－lnx＝－lnx有唯一零点x＝1.
当a＞1时，因
，
可见函数F（x）＝ax－x与f（x）在（0，＋∞）上有相同的零点.求出F′（x）＝axlna－1的唯一零点z＝
，于是F′（x）在（－∞，z）为负，在（z，＋∞）为正.从而F（x）在（－∞，z）递减，在（z，＋∞）递增，最小值为F（z）.
注意到F′（z）＝azlna－1＝0可得F（z）＝az－z＝
，当1＋lnlna＝0时即a＝ee－1时z＝
而F（z）＝0，即f（x）在（0，＋∞）上有唯一的零点.
当a＞ee－1时F（z）＞0，从而F（x）无零点，f（x）在（0，＋∞）上无零点.
当a＜ee－1时F（z）＜0，从而F（x）有两个正的零点，故f（x）在（0，＋∞）上有两个零点.
当a＜1时，lna＜0，此时F′（x）＝axlna－1＜0从而F（x）＝ax－x递减，注意到F（0）＝1＞0而F（1）＝a－1＜0，可知F（x）有唯一零点u∈（0，1）；由au＝u可得
，即f（x）至少有一个零点x＝u.
注意到如果c≠u使f（c）＝0，则由
得到aac＝c＝logaac，从而f（ac）＝0.而且由y＝ax递减和au＝u可知，若c＞u则ac＜u，若c＜u则ac＞u，可见f（x）在（0，u）上的零点和（u，＋∞）上的零点一一对应，只考虑（u，＋∞）上的零点即可.这里u＝u（a）是a的增函数.事实上，若0＜b＜a＜1，ax＝x且by＝y，若y≥x则必有ay＞by≥ax，从而推出y＜x的矛盾.这否定了假设y≥x，证明了y＜x.
求出f′（x）＝axln2a－
，它和g（x）＝有相同的零点和符号，故只要讨
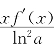论g（x）＝xa2－
即可.
求出g′（x）＝ax＋xaxlna＝ax（1＋xlna），它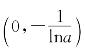在
上为正，在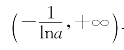
上为负，可见g（x）在
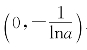上递增，在
上递减，在x＝－
取到最大值.
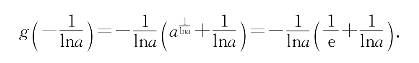
若0＞lna≥－e，即1＞a≥e－e，g（x）仅仅在一点取到非正最大值，于是g（x）除一点外均为负，故f（x）递减，只能有唯一零点.
在a＜e－e情形，由于
表明u（e－e）＝
，从而u＝u（a）＜u（e－e）＝
，故lnu＜－1.又由于au＝u＝logau＝
，可得g（u）＝uau－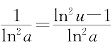
＞0，由g（＋∞）＝－
＜0，故g（x）在（u，＋∞）上有零点α，在（u，α）上为正而在（α，＋∞）上为负.这推出f（x）在（u，α）上递增且和（α，＋∞）上递减，由f（u）＝0可知f（α）为正，又因f（x）＝axlna－lnx，当x足够大时为负，可见f（x）在（u，＋∞）上有唯一零点x＝w.如前所述，它在（0，u）上也有唯一零点x＝aw.即在（0，＋∞）上有三个零点.全部讨论结果列表如下.
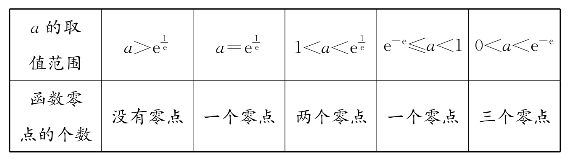
【注】方程axlna－lnx＝0等价于ax＝
logax，函数ax和它的反函数logax的曲线的交点的横坐标就是f（x）＝axlna－lnx的零点.
第11讲
习题11—1 解：（i）2excosx；
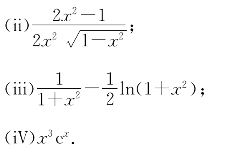
习题11—2 解
；
第12讲
习题12—1 解：（i）记y＝lnu，u＝1＋ev，v＝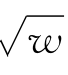
，w＝1＋cos2x；
则dy＝
，du＝evdv，dv＝
，dw＝－sin2xdx.
于是有
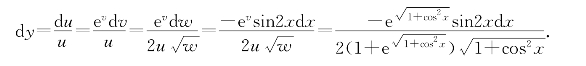
（ii）记y＝2u＋z，u＝sinv，v＝3＋lnw，w＝1＋x2，z＝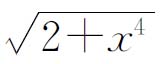
，则dy＝2uln2du＋dz，du＝cosvdv，dv＝
，dw＝2xdx，dz＝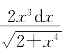
.于是有
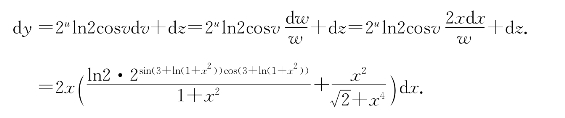
习题12—2 解：对曲线方程两端求微分得
2xdx＋（1＋sin2πx）2ydy＋2πy2sinπxcosπxdx＋ydx＋xdy＝0，
整理后为（2x＋2πy2sinπxcosπx＋y）dx＋（2y（1＋sin2πx）＋x）dy＝0，
因此有
.
分别将P和Q的坐标代入得两点处切线斜率kP＝－1和kQ＝－
.
第13讲
习题13—1 解：y′＝（arctanx）′＝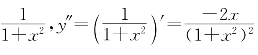
；
故有
习题13—2 解：y″＝ex＞0恒成立，故函数在（－∞，＋∞）下凸.由凸函数定义有
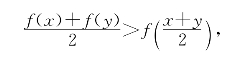
即ex＋ey＞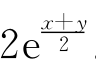
.
习题13—3 解：由y″＝－sinx可知对任意整数k有
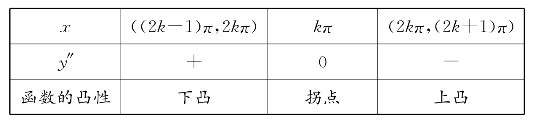
习题13—4 解：由y″＝－
可知
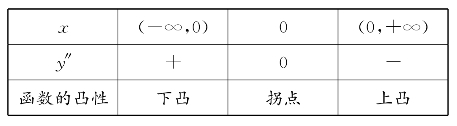
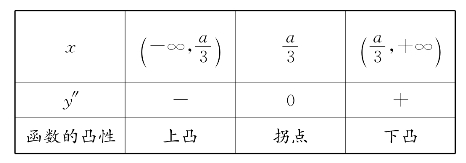
习题13—5 解：由y″＝6x－2a可知
习题13—6 证明：考虑函数g（x）＝f（x）－f（u）－f′（u）（x－u），
显然有g（u）＝0和g′（x）＝f′（x）－f′（u）.
由f′（x）递增可知
当x＞u时g′（x）＝f′（x）－f′（u）＞0，
故g（x）＞g（u）＝0；
当x＜u时g′（x）＝f′（x）－f′（u）＜0，
仍有g（x）＞g（u）＝0.即所欲证.
第14讲
习题14—1 解：方法1 设y＝x－1，则有x＝1＋y，所以
F（x）＝F（1＋y）
＝（1＋y）4－4（1＋y）3＋5（1＋y）2－7（1＋y）＋3
＝y4－y2－5y－2
＝（x－1）4－（x－1）2－5（x－1）－2.
方法2 设F（x）＝x4－4x3＋5x2－7x＋3
＝a＋a1（x－1）＋a2（x－1）2＋a3（x－1）3＋a4（x－1）4.
则F′（x）＝4x3－12x2＋10x－7
＝a1＋2a2（x－1）＋2a3（x－1）2＋4a4（x－1）3，
F″（x）＝12x2－24x＋10＝2a2＋4a3（x－1）＋12a4（x－1）2，
F（3）（x）＝24x－24＝4a3＋24a4（x－1），
F（4）（x）＝24＝24a4.
于是a0＝F（1）＝1－4＋5－7＋3＝－2，
a1＝F′（1）＝4－12＋10－7＝－5，
2a2＝F″（1）＝12－24＋10＝－2，
4a3＝F（3）（1）＝24－24＝0，
24a4＝F（4）（1）＝24；
可得F（x）＝（x－1）4－（x－1）2－5（x－1）－2.
习题14—2 解：计算出
（cosx）（2n）＝（－1）ncosx，
（cosx）（2n＋1）＝（－1）n（cosx）′＝（－1）n＋1sinx.
故（cosx）（2n
＝0，
从而得到泰勒展开式：
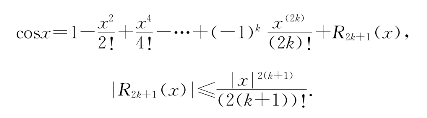
取x＝5°＝
≈0.0872664626＜0.09，可得
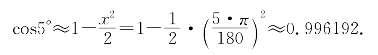
误差不超过
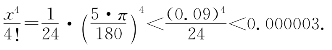
习题14—3 解：由（ln（1＋x））′＝
，
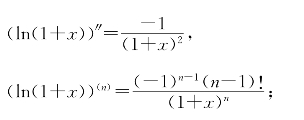
可知当－1＜x≤1时有
当x＞0，|Rn（x）|≤
；
当x＜0，|Rn（x）|≤ 
.
习题14—4 解：由f′（x）＝（arctanx）′＝
，得到（1＋x2）f′（x）＝1，
两端相继求导得
（1＋x2）f″（x）＋2xf′（x）＝0，f″（0）＝0
（1＋x2）f（3）（x）＋4xf″（x）＋2f′（x）＝0，f（3）（0）＝－2；
（1＋x2）f（4）（x）＋6xf（3）（x）＋6f″（x）＝0，f（4）（0）＝0；
（1＋x2）f（5）（x）＋8xf（4）（x）＋12f（3）（x）＝0，f（5）（0）＝24；
用数学归纳法，若有
（1＋x2）f（n）（x）＋2（n－1）xf（n－1）（x）＋（n－1）（n－2）f（n－2）（x）＝0，
则求导后得一般公式：
（1＋x2）f（n＋1）（x）＋2nxf（n）（x）＋n（n－1）f（n－1）（x）＝0.
取x＝0得递推式
f（n＋1）（0）＝－n（n－1）·f（n－1）（0），
从而得到 f（2k）（0）＝0，f（2k＋1）（0）＝（－1）k（2k）！
于是可以写出
如果取x＝1，得
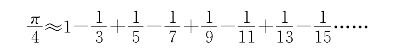
相邻两项合并得
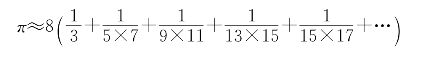
用计算机或计算器计算上式的右端10000项得π≈3.14154…….
第15讲
习题15—1 解：设S（u，v）是f（x）＝k·x＋c的一个积分系统，令F（x）＝S（c，x）.则F（x）是f（x）＝k·x＋c的甲函数.由f（x）＝k·x＋c差商有界，故F′（x）＝k·x＋c.另一方面已知
，
即
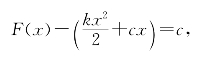
于是
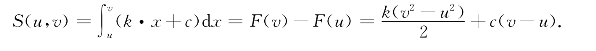
这也证明了S（u，v）是f（x）＝k·x＋c的唯一的积分系统.
习题15—2 解：函数floor（x）＝[x]积分系统S（u，v）的唯一性以及上一题中积分系统的唯一性都是单调函数积分系统唯一性的推论.
设f（x）在区间I上单调，S（u，v）和R（u，v）都是f（x）在I上的积分系统，下面证明恒有S（u，v）＝R（u，v）.
用反证法.不妨假定f（x）单调不减.若结论不真，则有I上的u＜v使
|S（u，v）－R（u，v）|＝a＞0.
将[u，v]等分为n段，分点为
u＝x0＜x1＜…xn＝u，
记H＝v－u，由f（x）在[u，v]上不减，故当x∈[xk－1，xk]时有f（xk－1）≤f（x）≤f（xk）.由积分系统的中值性可得：
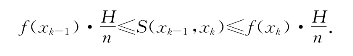
对k从1到n求和，并记F＝f（x1）＋…＋f（xn），得到：
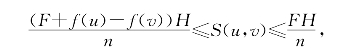
同理有
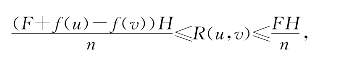
可见
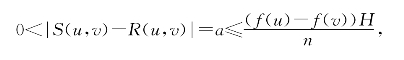
这推出n≤
，与n的任意性矛盾，证毕.
下面具体计算出S（u，v）.
若v＝k＋1为整数而v＞u≥k，下面证明必有S（u，v）＝k（v－u）.
由积分系统的中值性可知
于是只要证明不可能有S（u，v）＞k（v－u）即可.
用反证法，设S（u，v）－k（v－u）＝A＞0，取正整数N＞2使c＝v－
＞u，易知
k（v－u）＋A＝S（u，v）＝S（u，c）＋S（c，v）≤k（c－u）＋（k＋1）（v－c）.
整理得A≤u－c＝
，矛盾.
对于一般情形，由可加性得
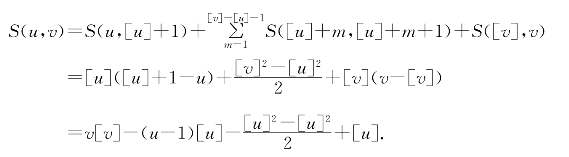
习题15—3 解：所求面积
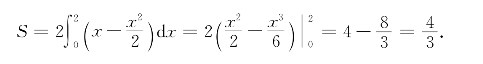
习题15－4 解：所求面积
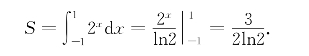
习题15－5 解
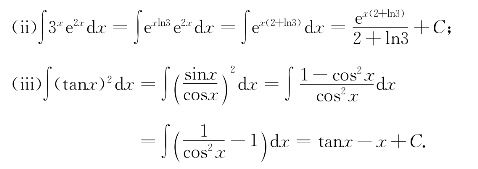
第16讲
习题16－1 解：（i）
；
而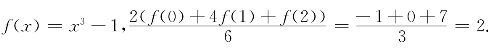
.
（ii）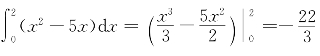
；
而f（x）＝x2－5x，
.
习题16－2 解：求出ln（1＋x）的马克劳林展开式：
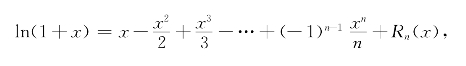
其中|Rn（x）|≤
.
取x＝1计算，为了误差不超过0.0001，可取1000项：
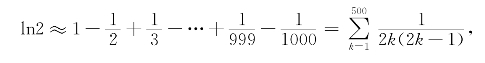
用计算机或计算器计算出
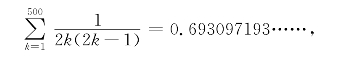
与ln2的8位有效数字0.69314718比较，误差小于0.00005.
若用114公式来计算，在[1，2]中取分点
和
，分别在
和
上使用114公式计算得
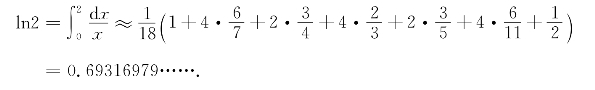
仅仅算了7项之和，误差就小于0.000025.
第17讲
习题17－1 解：使用公式
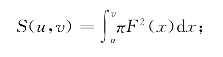
这里F（x）＝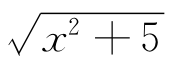
，u＝－2，v＝2.
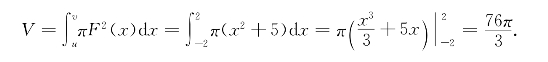
习题17－2 分析：用x表示小球下落的距离，F（x）表示小球所受的地心引力，则引力在[0，x]段对小球所做的功W（x）＝
，此功等于小球的动能，也就是
mV2（x）＝W（x），这里m是小球质量，而V（x）为小球的速度.设小球从开始下落到经过[a，b]段所用的时间为T（a，b），则有
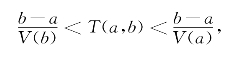
于是所求的时间为T（0，R）＝
.
计算：设地球质量为M，半径R＝6371千米，则
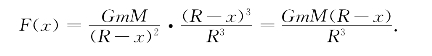
由于地表重力为GM＝R2g（重力加速度g＝9.8（米/秒2）），于是有F（x）＝
.进一步求出
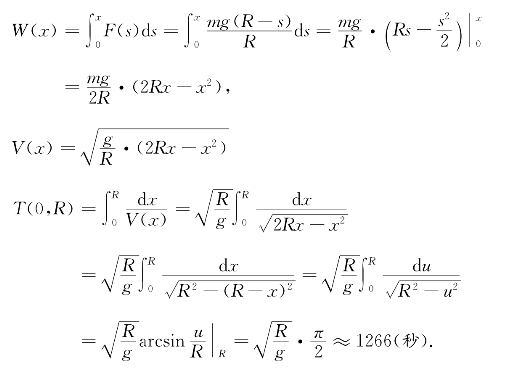
习题17－3 解：使用公式
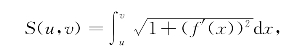
这里u＝0，v＝a，而f′（x）＝
，
所以所求曲线长度为
