狭义相对论
第一节 光速不变原理
时间与空间是否独立?
我们生活在四维时空(4-dimensionalspacetime)中。
首先,空间有三个维度(dimension),譬如任何一个物体都有长、宽、高。长度、宽度、高度都是可以发生变化的,加上时间,时间也是可以变化的,如此便有了时空的四维。当然,更准确的描述是,我们生活在3+1维的时空中。换言之,我们要描述在宇宙中发生的任何一个事件,都需要至少四个坐标(coordinate)。
例如,我给别人寄快递,要写对方的地址。地址其实就是一个三维的空间坐标,我肯定要写对方具体是在哪条街,几号,这里的街和号,就代表了两个空间坐标。我还要写对方是住在哪层楼,这就有了第三个空间坐标,即便对方家是别墅,也是有楼层的,别墅入口的楼层通常是一楼。
所以不管怎么样,写任何地址,都会有等效的三个空间坐标。除此以外,快递员要把包裹亲自交到对方手上,还得跟对方确认几点在家,也就是时间坐标。所以完全定下来一个事件,需要四个坐标,三个空间坐标和一个时间坐标。
这里就出现了一个看似不是问题的问题:时间坐标和空间坐标之间有关联吗?或者说,时间的流逝速度和你的空间位置,甚至是运动速度,有没有什么联系?
先别急着下定论,请先想象下面这样一个场景:我跟你两个人各佩戴一块手表,我们俩先把手表校准,然后你就坐着宇宙飞船,去太空游玩了一圈。我们假设两块手表都是非常精准的,那么请问:你去太空转了一圈回来之后,我们两人的手表指示的时间还会是一模一样的吗?
这个问题看似根本不是个问题,因为根据生活经验,既然两个人的表都很准,那不管是谁坐宇宙飞船出去转了一圈,表上的时间应该都是一样的。
这个答案其实就对应了牛顿(Isaac Newton)的绝对时空观(absolutespace and time)。什么是绝对时空观呢?就是牛顿,甚至爱因斯坦之前的所有学者都认为,时间的流逝是绝对的,它是独立运行的,跟空间没什么关系,全宇宙都可以使用同一个钟来计时。
当然,对于牛顿来说,这个结论其实是经验性(empirical)的,他并没有什么实在的证据。只是因为在我们日常生活中,哪怕你是个飞行员,天天开飞机,你的手表跟地面上的人的也不会有什么不一样。
但就是这样一个看似不是问题的问题,引起了爱因斯坦的注意。相对论的一个核心就是:空间和时间不是割裂的,它们并非相互独立,而是有非常紧密的内在联系。
相对速度(relativevelocity)
我们不妨再来想象第二个场景:现在的机场,都有水平传送带,可以让旅客走得快一些。假如有一个传送带,以10m/s的速度运动。这个时候,爱因斯坦站在传送带上,以相对于传送带1m/s的速度,顺着传送带的方向向前走。而传送带外的地面上站着普朗克。
问题是:传送带上的爱因斯坦,相对于地面上站着不动的普朗克的运动速度是多少?
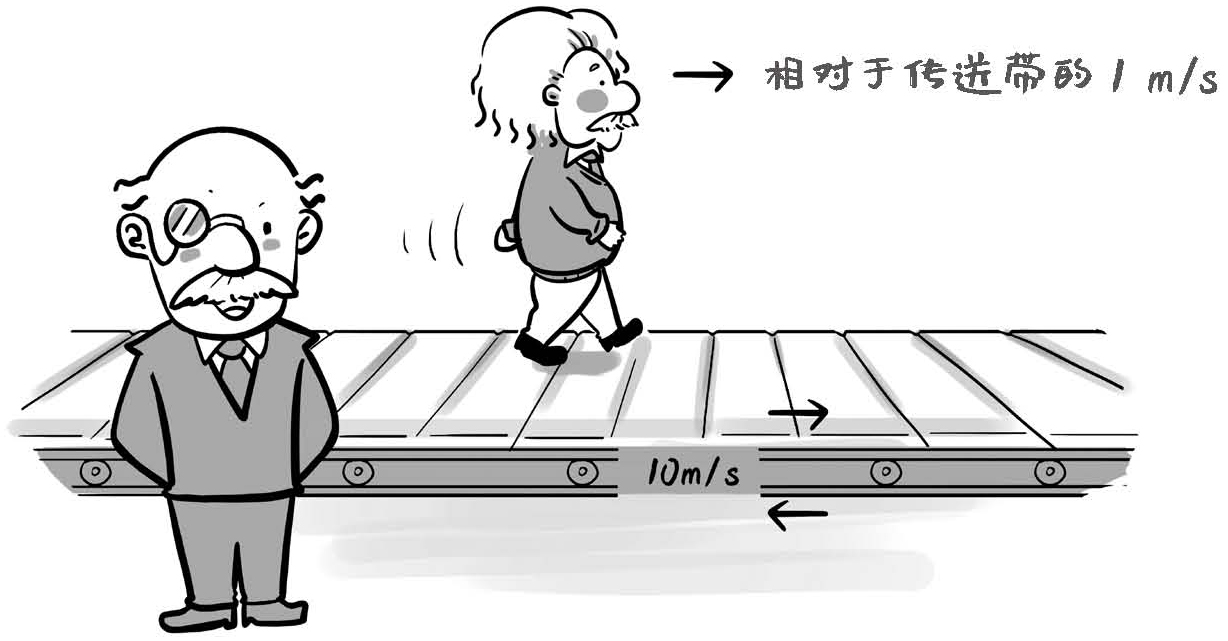
图1-1 普朗克和爱因斯坦相对速度
根据生活经验,这个问题不难回答。很明显应该就是传送带相对于地面的速度加上爱因斯坦相对于传送带的速度,也就是10+1=11,单位是m/s,这与我们的生活经验完全符合。而且即使你真的去做这个实验测量一下,得到的也一定是这个答案,没有任何疑义。
像这样的操作叫作伽利略变换(Galilean transformation):爱因斯坦相对于普朗克的速度=爱因斯坦相对于传送带的速度+传送带相对于普朗克的速度。
下面我们把场景稍微变一下:爱因斯坦就站在传送带上一动不动,手里拿着一个手电筒,他打开手电筒的开关,一束光向前射出。我们知道光速大约是每秒30万千米。
这个时候我再问:对于普朗克来说,它看到的手电筒射出的光的速度是多少呢?
根据之前的经验,这个问题同样可以用伽利略变换来回答:对于普朗克来说,他看到手电筒发出的光的速度,应该是每秒约30万千米,加上传送带的速度10m/s,也就是普朗克看到的光的速度应该大于爱因斯坦看到的光的速度。
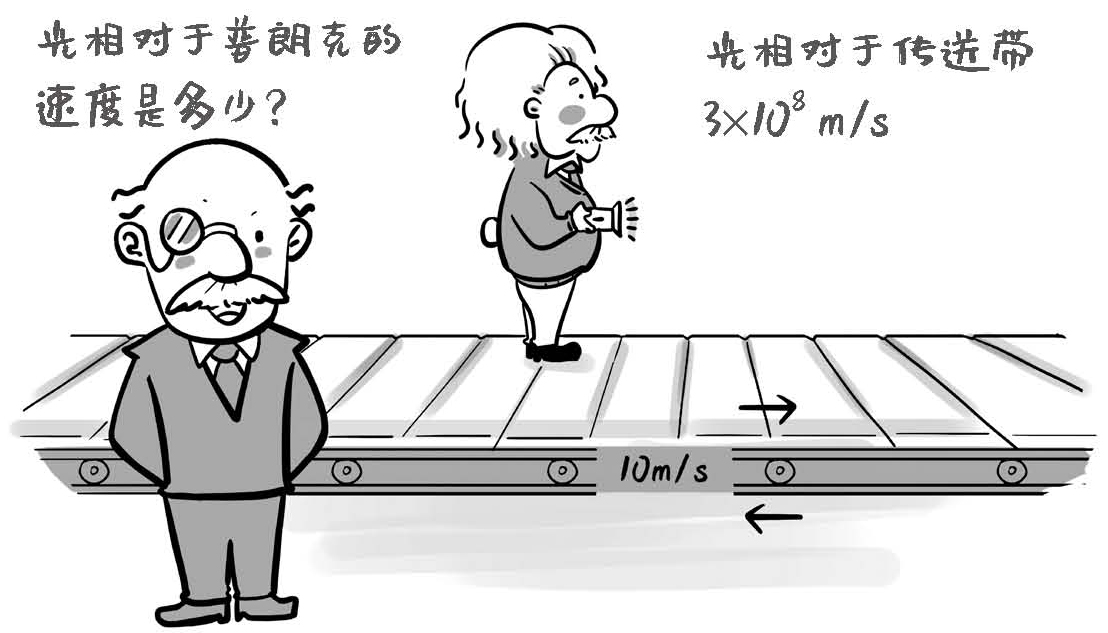
图1-2 光对普朗克的相对速度
先扣扳机还是子弹先飞出?
让我们姑且假设伽利略变换是正确的,来看看第三个问题——先扣扳机还是子弹先飞出?这个问题也可以说是一个思维实验。
现在想象普朗克拿着一把手枪,对着爱因斯坦开了一枪。我们假设爱因斯坦反应极快,他能看到子弹从枪膛里射出。下面考虑一下整个开枪射击的过程,这里面的因果关系(causality)一定是普朗克先扣扳机,然后子弹才从枪膛里射出。
也就是,爱因斯坦能看到两个事件的发生:第一个事件是普朗克用手扣动扳机,第二个事件是子弹从枪膛里飞出。爱因斯坦之所以能看见这两个事件,是因为普朗克扣动扳机的手上面的光射入了爱因斯坦的眼睛,并且子弹飞出的时候,子弹上面的光也射入了爱因斯坦的眼睛。
这里矛盾就开始显现了。先来想想上面第二个场景得到的结论,伽利略变换:扣动扳机的手上发出来的光,相对于爱因斯坦的速度,应该是手上的光相对于手的速度,加上手扣动扳机的速度;子弹飞出来时,子弹上的光相对于爱因斯坦的速度,应该是子弹上的光相对于子弹的速度,加上子弹相对于爱因斯坦的速度。
很显然,子弹射出枪膛的速度,要比手扣动扳机的速度快得多。子弹的速度能达到900m/s,世界上出拳最快的拳击手,出拳的速度也只有每秒几十米。这样对于爱因斯坦来说,子弹上射出的光的速度,要比扣动扳机的手射出的光的速度快。
这里就出现了一个巨大的矛盾,因为子弹射出的光更快,它会比扣动扳机那只手的光先一步到达爱因斯坦的眼睛里。爱因斯坦会先看到子弹从枪膛里射出,普朗克才扣动了扳机。这样对于爱因斯坦来说,整个事件的因果关系就颠倒了。
那问题出在什么地方呢?回想一下,之所以我们会得出这么一个荒谬的结论,是因为运用了伽利略变换。伽利略变换对于除了光以外的东西,似乎是很好用的。但是一旦在光速上做文章,就立刻破溃了。所以我们可以得出一个结论:至少在光速是多少的问题上,伽利略变换并不正确。
此处,我们就引出了相对论最核心的一条原理——光速不变原理。
光速不变原理说的是什么呢?简单理解就是,对于任何一个观察者,无论观察者处在什么运动状态,不论他的速度是多少,他探测到的光速永远都是一个恒定的值。
有了光速不变原理,我们再来看上面两个问题:传送带上的爱因斯坦打开手电筒,对于爱因斯坦来说,光速是每秒约30万千米,而普朗克看到手电筒发出的光,也是每秒约30万千米;扣动扳机的手发出的光相对于爱因斯坦是每秒约30万千米,子弹上射出的光相对于爱因斯坦来说,也是每秒约30万千米。这样的话,就不会出现子弹上的光比手上的光快的情况,也就不存在先看到子弹飞出,手再扣动扳机的情况了,因果关系也就不会颠倒了。
光速不变原理可以说是狭义相对论最核心的一条原理。但是除了光速不变原理之外,其实狭义相对论还有另外一条最核心的原理——狭义相对性原理。
狭义相对性原理比光速不变原理还要基础,我们甚至可以说光速不变原理是建立在狭义相对性原理基础之上的。或者说,有了狭义相对性原理,光速不变原理便是必然的。
狭义相对性原理说的事情其实非常简单:在不同的惯性参考系(inertial frame of reference)当中,所有物理定律都是一样。
这句话看起来很简单,但是细细琢磨起来,内容却很丰富。让我们来考虑一个场景:假设有两艘宇宙飞船,它们在宇宙中航行,它们都处在匀速直线运动状态,并且它们之间有相对速度,这个时候远处射来一束光,两艘飞船都尝试去测量这束光的速度。我们尝试论证这两艘飞船测出来的光速是一样的。
这两艘飞船都处在匀速直线运动状态,换句话说,它们都没有加速度(acceleration)。并且这两艘飞船,其实无法判断自己是不是在运动,因为不存在绝对的运动,也不存在绝对的静止,运动和静止都是相对的,两艘飞船能做出的判断只能是相对于对方来说,自己是运动的,或者它们可以说对方相对于自己是运动的。也就是这两艘飞船所处的参考系,完全是等价的。
既然是等价的,那根据狭义相对性原理,它们就应当拥有一样的物理定律。譬如说关于电磁学的物理定律,描述这个物理定律的方程是麦克斯韦方程组。两艘飞船各自的参考系当中的麦克斯韦方程组必须拥有一样的形式,否则就不满足狭义相对性原理。然而我们通过简单的计算就会发现,如果光速可变的话,不同参考系里的麦克斯韦方程组会有不同的形式,因此为了保证狭义相对性原理的成立,不同惯性参考系当中的光速必然是不变的,于是光速不变原理在麦克斯韦方程组的形式这个问题上,通过狭义相对性原理被推导出来了。
我们可以做一个类比,譬如说两架飞机在空气中做匀速直线运动,它们有相对速度。这个时候从远处传来一道声波(acoustic wave),两架飞机里的观察者尝试去测这道声波的波速,他们会获得不同的波速,这是因为声波的波速相对于空气介质是恒定的,但是两架飞机相对于空气介质的速度是不同的,因此它们可以测到不同的波速,但类似的情况放在时空本身是不成立的。因为光的传播不需要介质(medium),它可以直接在时空中传播,我们甚至可以粗略地认为,时空本身就是光传播的介质。
如果一艘飞船只是在太空中航行,在它周围什么东西都没有,它看不见任何天体,也看不见任何其他参照物,它甚至不能说自己的运动速度是多少,因为空间当中每一个位置都是一样的。任何一个参考系里的观察者都无法描述自己相对于时空本身的速度是多少,速度这个概念在观察者与时空本身这二者之间是破溃的。既然不存在观察者与时空这个介质之间的速度这样一个概念,但是他们又确实能够测量出光速,那就只存在一种合理的情况,就是不同观察者,只要他们的参考系都是惯性参考系,不存在加速度,则他们测量出的光速应当是一样的,否则就会使得不同的参考系相互之间不等价了,不等价的参考系当中未必有相同的物理定律,这就与狭义相对性原理冲突,因此,从这个角度来看,光速不变原理确实是狭义相对性原理的显性呈现。
第二节 “以太”并不存在
狭义相对论的根基——光速不变原理,说的是对于任何一个观察者,不管他的运动速度是多少,他去测量光速永远都会得到一个不变的值。既然说到了测量,那科学家究竟是如何验证光速真的是不变的 呢?
这就要说到19世纪末的著名实验——迈克耳孙-莫雷实验(Michelson-Morley experiment)。理解这个实验,需要建立三个阶段的认知。
波动如何传播?
第一阶段,我们要理解:机械波的传播是需要介质的。
光,其实就是电磁波。跟我们日常生活中接触到的声波、水波一样,电磁波也是一种波动,它是电磁场(electromagnetic field)的波动。
水波和声波很好理解,比如你往水里扔一块石头,这块石头让水泛起涟漪,涟漪会以石头为中心扩散出去;我们之所以能听到声音,是因为空气的波动传到了人的耳朵里,刺激了听觉神经。水波和声波分别是水和空气在做上下前后起伏的振动,而电磁波也是电场和磁场的强度(fieldstrength)随着时间的推移以及空间位置的变化而发生变化。
这里就出现了一个问题:机械波的传播是需要介质的。声音在空气里传播,空气就是声音传播的介质。我们上中学的时候都做过一个实验:把一个正在响的闹钟放在玻璃罩子里,如果你把玻璃罩子里的空气不断抽出,就会发现闹钟的声音越来越小,等空气都抽完了,你也听不到闹钟的声音了。这就是因为作为传播介质的空气不存在了,声音也就无法传播了。
但电磁波的传播似乎不需要介质,宇宙飞船跟地球通信,用的就是电磁波。在太空中,没有水也没有空气,电磁波是怎么传播的呢?
于是早年的科学家们就提出了一种假想的介质,叫作以太(ether)。以太这种东西看不见摸不着,弥漫在整个宇宙空间当中。光,也就是电磁波就是通过以太这种介质进行传播的。迈克耳孙-莫雷实验最初的目的就是去寻找以太这种物质。
波的干涉现象
这就来到了第二阶段的认知,我们要理解一个物理现象:只要是波,不管是声波还是光波,甚至我们在之后的内容中会介绍的物质波,它们都存在一个现象,叫作波的干涉(interference)。
图1-3 余弦波
一束波,准确说,一束横波,它的样子大概是一条上下振动的曲线,中学里学过的有正弦波(sine wave)和余弦波(cosine wave)。波有波峰和波谷。
现在想象一下,如果你在冲浪,当一排海浪冲刷过来的时候,你就会随着海浪上下运动起来。当波峰经过你的时候,你处在最高点;波谷经过你的时候,你处在最低点。
再考虑如果有两排振动情况相同的海浪同时向你冲过来,两排浪都经过你的时候你会怎么振动?其实就是把两排浪的运动直接相加:如果两排浪都让你往上运动,你的运动幅度就比一排浪的时候更大;如果一排浪让你往上,另外一排浪让你往下,你就会折中一下,甚至干脆不动了,这就是波的叠加原理(superposition principle)。
只要是波,都满足叠加原理。如果换成是光波,假设有两束光波的波峰同时经过,那振动幅度更大,能量更强,就会显得更明亮。如果是一个波峰和一个波谷经过,它们的振动相互抵消,振幅小,能量弱,就会变暗。
所以当两束光打到同一片区域发生干涉现象时,有的位置是波峰碰波峰,或者波谷碰波谷,有的位置是波峰碰波谷,波峰波谷相遇区域内就会形成明暗相间的条纹。
迈克耳孙-莫雷实验的原理
第三阶段,我们来了解迈克耳孙-莫雷实验的原理,它就是基于波的干涉现象发明出来的。
迈克耳孙(Albert Abrahammichelson)和莫雷(Edwardmorley)是两位物理学家的名字,他们因为这个实验获得了1907年的诺贝尔物理学奖。这个实验是为了验证以太是否存在。
首先要明确一点,波相对于它的介质的速度是恒定的。
我们说声速(speed ofsound)约是340m/s,其实指的是声音相对于空气的速度。空气静止的时候,声速对于人来说也约是340m/s,但如果声音是伴随着一阵风迎面吹来的,这个时候声音相对于你的速度就不是大约340m/s了。
以太被假设为光的传播介质,所以光相对于以太的速度是恒定的,大约每秒30万千米。
当时的科学家们假设以太弥漫在全宇宙空间中,相对于太阳是静止的。地球绕太阳公转的速度大约是30km/s,所以地球是在以太中穿行的。人站在地球上,实际上是时时刻刻都有一阵“以太风”以30km/s的速度吹来,因为以太相对于太阳静止,而地球又相对于太阳公转,所以地球相对于以太是运动的。
迈克耳孙和莫雷做了一台仪器,名叫迈克耳孙干涉仪(Michelson interferometer)。首先左边是一个光源,它会发出一束光,打到中间的分光镜上;分光镜会把这束光分为两束,一束继续向右,一束垂直于原方向向上射出;然后在右边和上边各放一面镜子,镜子会让两束光回弹;这两束光在中间汇聚以后,再被一个装置汇聚到下方。这里要明确的是,两面反射镜跟中间分光镜的距离,须调节至完全相等。
那么根据波的干涉原理,这两束光汇聚以后打到同一个地方,就会发生前面所说的干涉现象,产生一组明暗相间的条纹。
具体干涉的形态跟什么有关呢?跟两束光传递到干涉仪下面观察处的时间差有关。不妨想象一下,我们假设有两束波,他们的波长完全相同,传递的速度也完全相同,那么两束波的运动周期也是一样的。
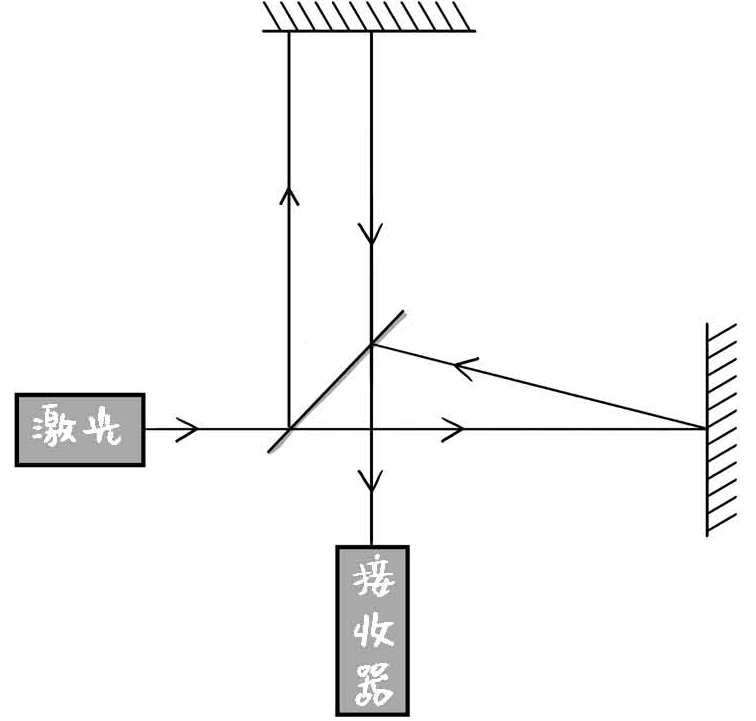
图1-4 迈克耳孙干涉仪原理图
我们不妨假设波的周期(period)是2s,也就是一个完整的波需要两秒钟才能传递完,如果两束波到达的时间差是两秒钟的整数倍,那么这两束波的步调就是完全一致的,波峰和波谷一定是同时到达的。但是如果两束波到达的时间差是1s,或者说是奇数秒,3s,5s,7s,那么就会出现波峰遇到波谷的情况。
现在我们来调节一下整台实验仪器的方位,让向右传播光的方向,刚好是逆着以太风运行的。那么相应地,向上传播的光的方向,就垂直于以太风。
这种情况下,如果以太存在,两束波到达下方汇聚的时候,一定会存在一个时间差。道理很简单,因为向右边传播的光到达右边的镜子再弹回来,去的时候是逆风,回来的时候是顺风。所以对于这个放在地球上不动的干涉仪来说,光去的时候和回来的时候速度是不一样的。并且光一来一回走过的路程,也就是右边镜子到中间分光镜的距离,是可以量出来的,这样就可以计算出这一来一回的时间。
同理,向上射出的光虽然既不逆风也不顺风,它一来一回的时间也能计算出来。最后我们会发现这两个时间是不一样的,所以这两束光汇聚后会形成特定的干涉条纹。
这个时候如果转动这台干涉仪,比如让它转过45°。那么在转动的过程中,两束光相对于以太风的运动方式一直在改变,所以它们相对于实验仪器的速度也一直在变。可以想象,两束光的时间差在转动过程中也一直在改变,最后就会影响到干涉条纹。也就是如果以太风存在的话,干涉条纹的形状会发生变化。
然而这个实验的结果令人大失所望:不管你怎么转动实验仪器,干涉条纹都不发生一丁点的变化,实验结果跟以太的基本假设完全不一致。
所以,迈克耳孙-莫雷实验的结果向我们证明了两件事:
(1)以太并不存在,光可以在真空中传播,不需要任何介质;
(2)光速跟测量者的运动状态没有关系,它在任何情况下都是不变的。很显然,地球的公转完全没有影响到我们测量的光速大小。
并且,科学家充分发挥了严谨的实证精神,在地球上的各种地方都做过这个实验。甚至到了21世纪还有人去做这个实验,实验设备达到了1/1016的精度,仍然没有得到任何与最初的实验不同的结果。
这就印证了我们在序言里介绍的物理学研究的方法论:先归纳,基于波相对于介质速度不变这一点,假设光相对于以太的速度也不变;再演绎,推导出如果以太存在,会有干涉条纹的变化发生;最后验证,验证的结果跟演绎不符,就说明一开始的归纳错了,以太并不存在。
到这里,我们就通过实验验证了光速不变原理。如果你要继续问,为什么光速是不变的?这个问题就无法回答了,因此它是基本原理,最多可以说是因为狭义相对性原理,则光速必须不变。原理通过归纳法得来,是逻辑推理的源头,它不能用演绎法证明出来,也就不能问为什么,只能说世界的规律本来如此,只能通过实验去验证,它只存在被证伪的可能,但无法通过逻辑演绎进行证明。我们只能把光速不变原理当成推理的原点,承认它的正确性,再由此出发,看看这个原理能推导出什么结论。
第三节 钟慢效应(time dilation)
在中国古代的神话体系中,有“天上方一日,地上已千年”的说法,天上一天等于人间一千年。其实,如果考虑相对论效应的话,这完全是可能的,只要天上的神仙们运动得足够快就可以了。
运动速度越快,时间流逝的速度就越慢,这种现象叫作钟慢效应,是狭义相对论的必然导出。
速度越快,时间越慢
假设有一列火车正在行驶,爱因斯坦站在火车里一动不动。车的地板上有一盏灯,爱因斯坦可以控制手里的开关,让地板上的灯向上打出一束光。然后火车顶上有一面反光镜,刚好可以把光反射下来,被一个紧挨着灯的接收器接收。爱因斯坦手上还有一个计时器,当光射出的时候,他会按动计时器,然后等光反射回来被接收器收到的时候,爱因斯坦会再按一次计时器。这样的话,计时器显示的时间,就是光从射出再被反弹回来,最后被接收器收到的时间。当然,这里我们假设爱因斯坦的反应奇快,他掐表没有任何时间差。
与此同时,火车向前运行。而地面上还有一个观察者普朗克,普朗克站在地面上不动,他也要测量光从火车的地板上射出到被反射回地板,再被接收器收到所用的时间。
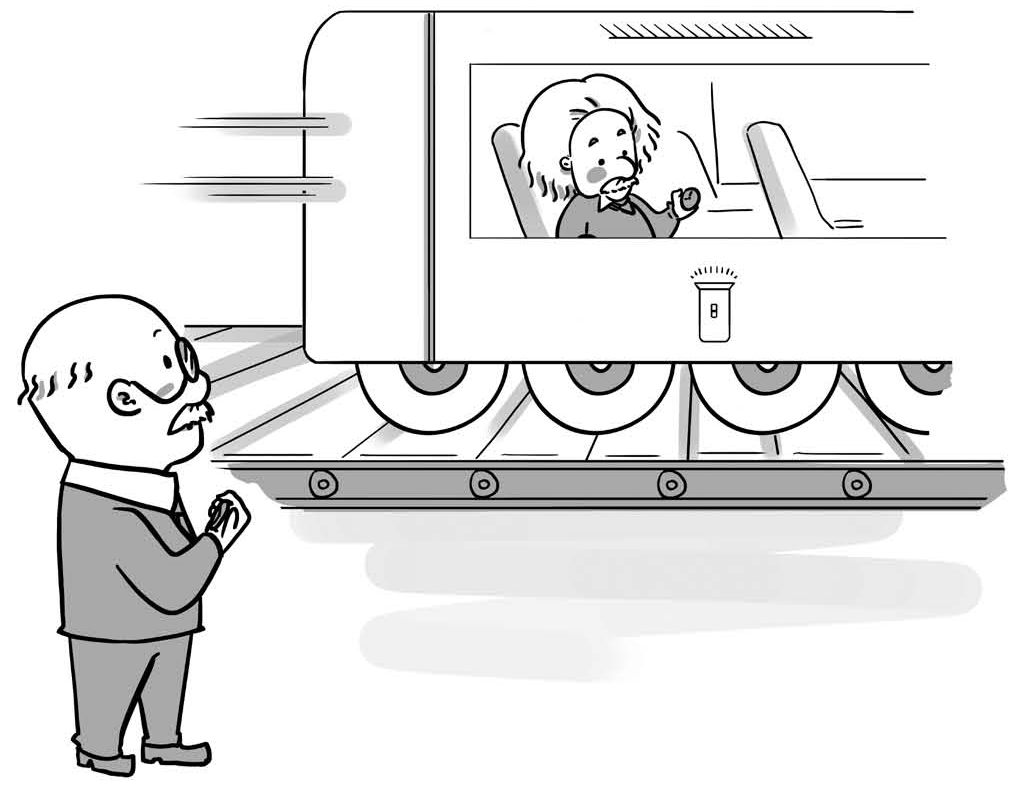
图1-5 普朗克和爱因斯坦的火车游戏
我们的目的是去比较一下,同一件事情,也就是光从射出到被接收,在两个不同的观察者看来,所用的时间是不是一样的?
牛顿会告诉你,这两个时间肯定是一样的。但是现在有了光速不变原理,这两个时间真的是一样吗?
首先,对于爱因斯坦来说问题很简单,他测量到的时间,就等于车厢的高度乘以2再除以光速。因为一来一回,光走过的距离是车厢高度的两倍。
其次,看看地面上的普朗克。由于在光传播的过程中,火车已经在往前走了,所以对于地面上的普朗克来说,车顶的反光镜,已经前进了一段距离,所以普朗克看到的光走过的距离,是直角三角形的斜边的两倍。很显然,直角三角形的斜边是大于直角边的,也就是车厢的高度。
虽然普朗克看到的光从发出到被接收的整个过程,跟火车上的爱因斯坦看到的是一样的,对应于同一个事件的开始和结束。但是很明显,对于普朗克来说,它看到的光走过的路程要比爱因斯坦看到的长。
而根据光速不变原理,普朗克看到的光的速度跟爱因斯坦看到的是一样的,都是每秒约30万千米。时间等于路程除以速度,对于光从发出到被接收这件事,普朗克观察到的时间就比爱因斯坦观察到的时间要长。如果普朗克可以看到爱因斯坦的手表,他就会发现爱因斯坦的手表比自己的手表走字慢,这就是钟慢效应。也可以换一种说法:对于地面上的人来说,火车上的人的时间膨胀了(dilated)。可能火车上的人的1s,就等于地面上的人的2s,1s当2s用,所以膨胀了。
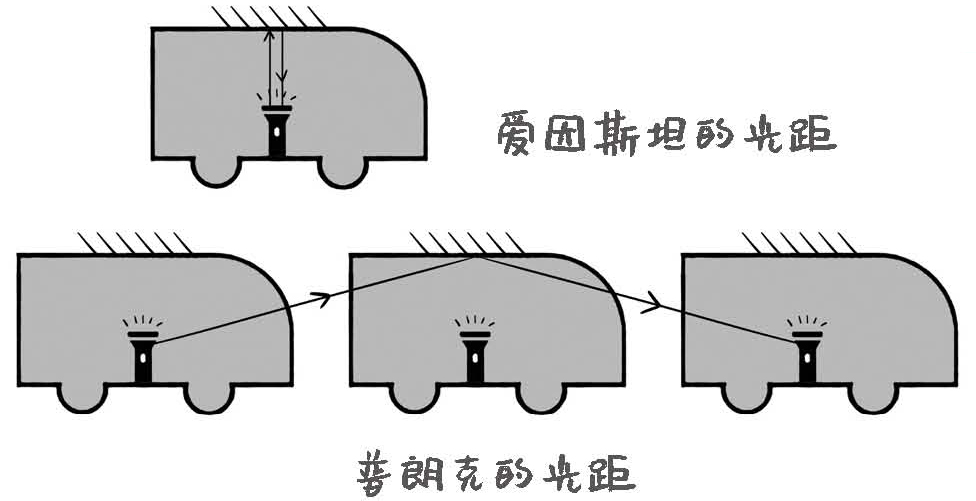
图1-6 钟慢效应模拟
所以“天上方一日,地上已千年”是完全有可能的,只要天上的神仙运动的速度非常快,理论上确实可以做到这个效果。那天上的神仙要运动多快呢?根据计算,他们的运动速度必须达到光速的99.9999999996247%,才能有这个效果。
自己不觉得慢,别人看你慢
初步了解了钟慢效应后,我们来看看如何具体理解钟慢效应。有一个关键点要牢记,钟慢效应是指当你处于高速运动的过程中,别人看你的钟走得慢了,而不是你自己看自己的钟也走得慢。
比如你吃一顿饭大概要半个小时。这个时候你坐上一艘宇宙飞船,就算宇宙飞船运动的速度非常快,以接近光速在运动,你在这艘宇宙飞船上吃一顿饭,对你自己来说,大概还是需要半个小时。不管你以什么样的速度运动,都不影响你自身对于时间流逝的感受。
只不过这个时候,如果地面上有人在观察你吃饭,对于他来说,你吃饭的过程就像电影里的慢镜头,你的动作变得非常缓慢。最终效果是,等你坐着宇宙飞船吃完一顿饭回来,你地球上的亲戚朋友可能已经老了10岁了。

图1-7 天上一日,地上千年
钟慢效应,指的是不同的参考系,在有相对运动的时候,它们对于同一件事情时间流逝的快慢,感受是不一样的。而自己对于自己参考系里面发生的事件,时间快慢不会有任何变化,这才是对钟慢效应的正确理解。
钟慢效应的证据
钟慢效应听上去非常神奇,但是要明显看到时间变慢的效果,需要运动速度非常接近光速。很显然,在现实世界中,宏观物体根本没有办法加速到如此快的速度。但是在微观世界,钟慢效应已经得到了证明。在粒子物理(particle physics)领域,科学家们对宇宙射线(cosmic rays)的研究,已经充分地证明了钟慢效应的存在。
宇宙射线中有各种各样的粒子,这些射线在射向地球的过程中,是以接近光速的速度运动的。射线中的粒子在进入大气层以后大多会经历衰变(decay),衰变成其他粒子。根据计算,很多粒子的衰变周期,或者说它的寿命,是非常短的。如果我们用它的寿命乘以它的运动速度,就能算出这种粒子在衰变前能够走过的距离。结果发现,这个距离远远小于大气层的厚度,也就是说,如果这些粒子的寿命真的这么短的话,它们是无法到达地面,被人类的实验仪器探测到的。
但事实并非如此,我们通过实验手段,探测到了很多宇宙射线中的粒子,这个事实本身就可以用来验证钟慢效应。因为对于地球上的观察者来说,宇宙射线中的粒子运动的速度非常快,所以它的时间是会膨胀的。可能原来一个粒子的寿命只有几纳秒(nanosecond,10-9s),但只要它的速度够快,它的寿命在地球上的人和实验仪器看来,可能有几十纳秒、几百纳秒。这样的话,这些粒子就有充足的时间可以到达地球表面,钟慢效应就得到了验证。
运动起来的物体,它的时间流逝相对于其他观察者会变慢,这是相对论效应的展现。它的道理十分简单,完全是通过光速不变原理推导出来的。理论上,飞机上的飞行员和空乘人员整天在空中飞,他们的时间流速就要比地面上的人慢一些,也就是他们要比地面上的人年轻一些。只不过这种时间膨胀的效应微乎其微,可以完全忽略。
根据计算,我们假设一位空乘人员工作20年,一天工作8小时,等他的整个飞行生涯完成后,算下来他会比地面上的人年轻大约0.00006s。所以尽管相对论如此反常识,但是我们平时的运动速度都太慢了,相对论的效果在日常生活中小到可以完全忽略。
第四节 尺缩效应(length contraction)
这一节我们继续介绍相对论带来的另外两个神奇效果。
第一个叫作尺缩效应,顾名思义,就是一把相对地面在运动着的尺子,长度会在尺子运动的方向上缩短。这里的缩短,要再强调一下,是地面上,相对于地面静止的观察者测量到的尺子长度会变短。但是如果尺子上有另一个观察者的话,他测量到的尺子长度还是原来的长度,因为相对于尺子上的观察者来说,尺子并没有运动。
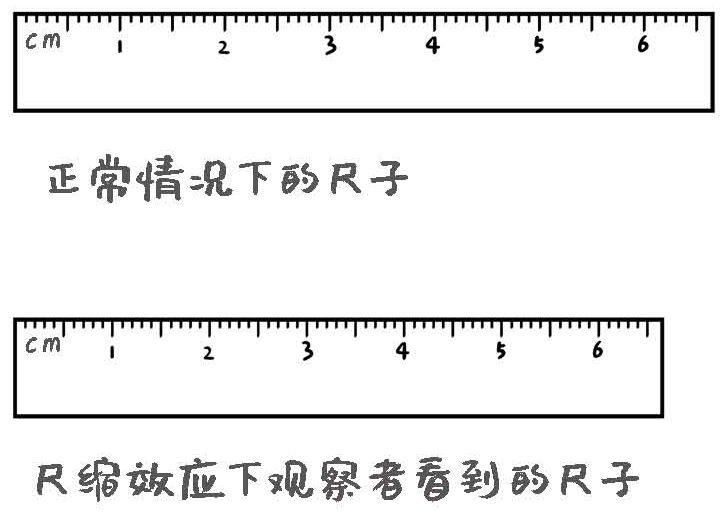
图1-8 尺缩效应
而且相对于地面上的静止观察者来说,尺子只是在它运动的方向上缩短了,垂直于运动方向的长度不会改变。如果一个正方形在沿着它的一条边的方向运动,它就会变成一个长方形。如果正方形是沿着它的一条对角线运动的话,它就会变成一个菱形。
如何定义长度
仍然用一个思维实验来解决这个问题。既然是要测量尺子的长度,那就要先定义一下,尺子的长度在不同的参考系中是怎么量出来的。

图1-9 爱因斯坦和普朗克的尺子游戏
假设这个时候爱因斯坦站在地面上不动,他可以这样测量尺子的长度:当尺子的头部经过爱因斯坦的时候,他记录下一个时间,与此同时,在尺子的头部做一个记号;当尺子的尾部经过他的时候,他也记录下一个时间,并在尺子的尾部也做一个记号。这样的话,对于爱因斯坦来说,他量出来的尺子的长度,其实就是他记录下来的两个时间差,乘以尺子的运动速度。
再来看看站在尺子上的普朗克,他要如何去测量尺子的长度?刚才说了,地面上的爱因斯坦在尺子的头部和尾部都做了记号,那么对于尺子上的普朗克来说,他只要也记录下爱因斯坦做这两个记号的时间差,再乘以爱因斯坦相对于他的速度,其实也就是这把尺子的速度,就可以了。最后再去比较这两个时间差之间的关系,就可以得出尺子的长短到底变化了多少。
尺缩效应的推导
根据上一节我们讲钟慢效应的过程,直觉上能感觉到,这个时间差在普朗克和爱因斯坦看来,肯定是不一样的。类比上一节钟慢效应的结论,对于爱因斯坦来说,他给尺子的头部和尾部做记号这两件事,是在同一个地方发生的,因为他自己的位置没有变。但是对于尺子上的普朗克来说,爱因斯坦在头部和尾部做记号这两件事,不是在同一个地方发生的。
这是不是很像上一节做的钟慢效应的思维实验?在钟慢效应里,光从地板上射出再回到探测器这两件事,对于爱因斯坦来说是在同一个地方发生的。但是由于火车在移动,对于普朗克来说,这两件事不是在同一个地方发生的。所以前后发生的两件事,如果对于一个观察者来说是在同一个地方发生的,他测量出来的时间,一定比另一个看这两件事不在同一个地方发生的观察者,测量出来的时间要短。
同理,对于刚才测量尺子长度的实验,爱因斯坦所用的时间肯定也没有尺子上普朗克用的时间长。因为给尺子头部和尾部做记号这两件事,对于爱因斯坦来说是在一个地方发生的,而对于普朗克来说不是。
有了爱因斯坦做记号的时间差比普朗克看到记号的时间差要短这个结论,我们就知道:爱因斯坦测量到的尺子的长度,一定比普朗克测量出来的更短。因为爱因斯坦的时间差更短,而尺子的长度被定义为尺子运动的速度乘以两个记号的时间差。这就是尺缩效应,对于一个观察者来说,任何一个运动的物体,在它运动方向上的长度会缩短。
当然,如果纯粹从狭义相对论的理论性推导来说,应当用洛伦兹变换(Lorentz transformation)对尺缩效应进行推导,还必须要强调,尺子长度的定义,必须是同时性地获得尺子两端在两个不同参考系当中的坐标,坐标之间的距离才能被定义为尺子的长度。所以严格来说,我们上面的定性推导方法并非完全正确,不过其结论与通过洛伦兹变换进行的理论性数学推导的结论是一致的。
上一节我们讲到,地球上能够接收到很多宇宙射线中的寿命很短的粒子。根据钟慢效应,因为粒子运动速度快,所以对于地球上的观察者来说,粒子的寿命变长,足够支撑它们穿越大气层来到地球表面。
我们现在变换到粒子的参考系,看看这件事情该怎么解释。
假设你现在是宇宙射线中一个寿命很短的粒子,你在自己的参考系里,看自己的寿命还是很短,但是你又能穿越大气层到达地球表面,恰恰是因为尺缩效应。由于你的速度相对于地球很快,大气层到地球表面的这段距离,对于你来说大大缩短了,你在衰变之前还是可以到达地球表面的。
再看相对速度
再来看关于狭义相对论的一个神奇效果,就是我们在前文中提到的有关相对速度的例子。再来回顾一下,爱因斯坦在机场传送带上走路,传送带的速度是10m/s,爱因斯坦相对于传送带的速度是1m/s;普朗克站在传送带外的地面上,问普朗克看爱因斯坦的速度是多少?伽利略变换给出的答案很简单,就是两个速度相加,10+1=11,单位是m/s。但是我们现在已经学习了钟慢效应和尺缩效应了,这个答案就不那么显而易见了。
如果爱因斯坦在传送带上走了1s的时间,他就走了1m的距离。然而由于尺缩效应和钟慢效应,这个1m在普朗克看来是不到1m的,这1s在普朗克看来也不止1s。速度等于距离除以时间,现在分子比1m小,分母比1s大,所以可以很快得出结论:普朗克看爱因斯坦相对于传送带的速度肯定不到1m/s,普朗克看爱因斯坦的总速度肯定也不到11m/s。
还有更神奇的,回顾一下爱因斯坦打开手电筒的思维实验。手电筒的光相对于爱因斯坦的速度是光速,如果按照伽利略变换,普朗克会发现他测量到的光速要比爱因斯坦测量到的光速大。但是如果按照相对论的速度叠加的方法去计算的话,会发现普朗克测量到的光速,和传送带上爱因斯坦测量到的光速是完全一样的,这就刚好符合光速不变的基本假设,狭义相对论也就完美地自圆其说了。
第五节 为何光速无法超越
全世界最广为人知的物理学方程——质能方程(mass-energy equivalence),E=mc2,也就是能量等于质量乘以光速的平方。这个方程到底在说什么?它又是怎么来的?光速为什么无法超越?
在理解质能方程之前,要先介绍一下相对论中另外一个特殊的效果,那就是一个运动的物体相对于地面上的观察者来说,它的质量会变大。这一相对论效应的证明过程比较复杂,但我们还是可以尝试理解一下。
动量守恒(conservation ofmomentum)
首先我们要介绍物理学当中的一个重要概念——动量(momentum)。什么是动量呢?简单来说,一个物体的质量乘以它的速度,就是这个物体的动量。可以粗略地认为,一个物体动量的大小,正比于要让这个运动的物体停下来的难易程度。很显然,一个物体的速度越快,就越难让它停下来,比如超速的汽车不容易刹车。而在速度一样的情况下,质量越大,也越难停下来,一辆时速100千米的大货车肯定要比一辆时速100千米的小轿车更不容易停下来。所以动量的公式写出来就是质量乘以速度,它表征了一个物体运动的“量”的多少。
关于动量有一条铁律,叫作动量守恒定律。说的是一个物理系统,在没有外力的作用下,不管这个系统内部发生怎样的相互作用,不论是碰撞、摩擦、融合,整个系统的动量从头到尾不会发生任何变化。
比如一个小球,质量是m,运动的速度是v,它撞向一个质量是M的大球,大球的速度是V。
第一种情况,两个球是很光滑的,撞完之后,又各自分开,获得了两个不同的速度,小球的速度从v变成了v1,大球速度从V变成了V1。那么动量守恒告诉我们,不管v1和V1具体是多少,碰撞之后的总动量,mv1+MV1一定等于碰撞前的总动量mv+MV。
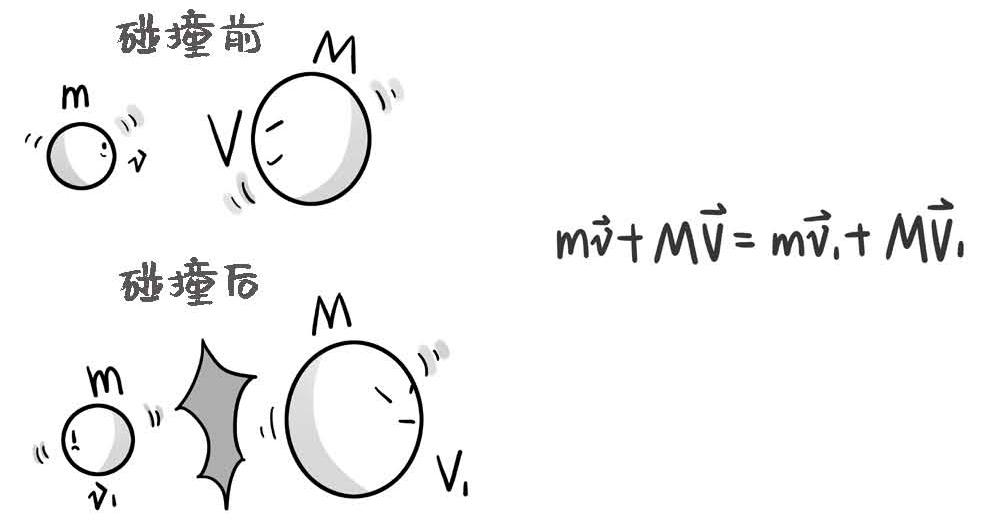
图1-10 碰撞前后动量守恒
同样,假设两个球之间粘了一个口香糖,碰撞之后它们不再分开,获得了一个共同的速度V2,那么碰撞之后的总动量mV2+MV2,也一定等于mv+MV。因为如果把这两个球当成一个整体,这个整体在碰撞前后是不受外力作用的,动量一定守恒。
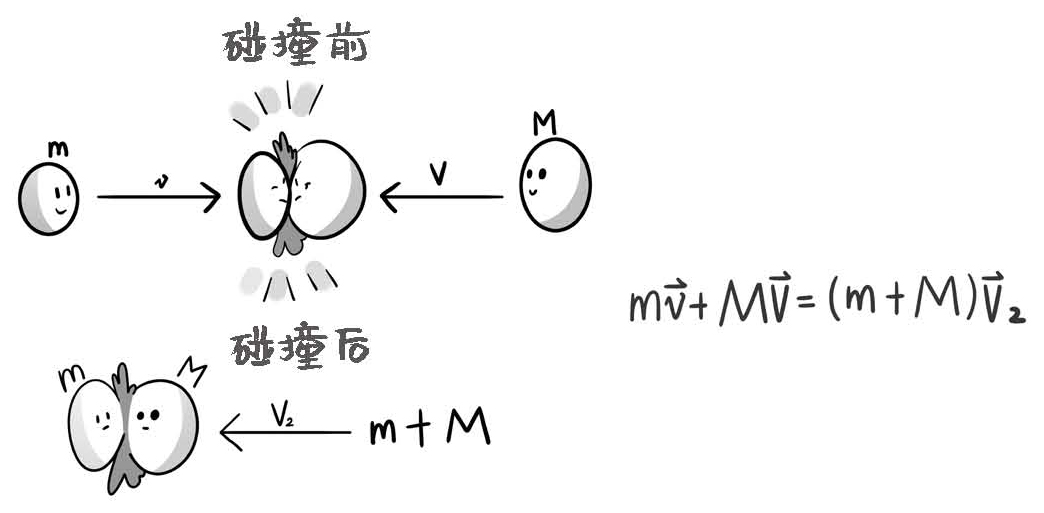
图1-11 碰撞前后动量守恒
其实与这两个球粘在一起相反的过程动量也是守恒的。比如有一个大球M,以速度V在运动,它里面装了炸药,炸药爆炸以后,M分裂成了两个小球,质量分别是m1和m2,速度分别是v1和v2。这种情况下,不管这几个数值具体是多少,一定满足MV=m1v1+m2v2。因为大球爆炸前后,系统的整体不受外力作用。
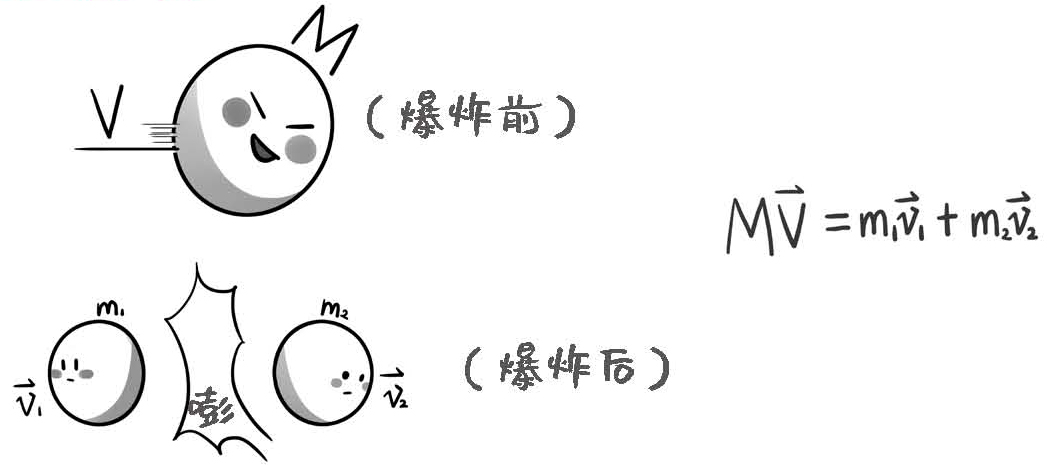
图1-12 爆炸前后动量守恒
速度越快,质量越大
有了动量守恒的知识之后,就可以解释为什么运动着的物体质量会增加。
我们想象这样一个物理过程:假设有一个大球M,它正以速度v相对于地面的观察者普朗克运动。大球上也有一个观察者,还是爱因斯坦,他相对于大球M是不动的。这个时候爱因斯坦在大球上放了个炸弹,并操控它突然爆炸,大球被炸成了大小相同的两个小球向两边飞出。并且它们飞出去的时候,相对于爱因斯坦的速度都是v,爱因斯坦相对于普朗克的速度保持不变,还是原来的v。
对于地面上的普朗克来说,左边这个小球由于爆炸后获得了向左的速度v,刚好抵消了原来作为大球的一部分向右运动的速度v。所以对于普朗克来说,这个小球就停下来了,速度为0。再看另一个向右运动的小球,它相对于爱因斯坦来说有一个向右的运动速度v,但这个时候普朗克看这个小球的速度,可就不是2v了。参考上一节介绍的考虑相对论效应后的速度叠加,跟之前讲过的传送带的问题是一样的。所以大球爆炸后,向右运动的小球相对于普朗克的速度,是小于2v的。
到这里就可以用动量守恒了,整个系统由于没有受到外力的作用,爆炸前和爆炸后相对于普朗克的动量应该是不变的。爆炸前的动量是大球的质量乘以大球的速度,等于Mv。爆炸之后,左边的小球停了下来,速度是零,所以对动量没有贡献。但是右边那个小球,质量假设是m,速度比2v要小,如果动量要守恒的话,就可以得出一个结论:m的质量要大于M的一半。

图1-13 速度越快质量越大
而在不考虑相对论效应的情况下,M炸成两个质量相等的小球,每个小球的质量应该精确地等于M的一半,但事实是根据动量守恒以及相对论效应,这小球的质量必须大于M的一半,所以运动的物体质量会增大的结论就这样得出来了。
E=mc2
既然已经知道了运动的物体质量会增大,就能推导出爱因斯坦著名的质能方程E=mc2。
中学时我们都学过动能(kinetic energy)这个概念。在牛顿体系中,用力对一个物体做功(work),推着它走一段距离,这个物体的动能就会增加。有了对于动能的定义之后,结合牛顿第二定律,再加上简单的微积分,就可以推导出动能的表达式:动能等于质量乘以速度的平方再除以2。在经典力学中,物体的动能就是这个形式。
在经典力学里,质量是不变的。而上面已经证明了,随着物体的速度加快,质量也会变大。所以如果真要完整地表达一个物体的能量,我们必须把质量的增加计算进去。如果把质量随着速度的变化代入动能的公式,再进行一个相对复杂的微积分操作,就很容易得出,一个物体的总能量,E=mc2,这里的m是考虑了相对论效应之后的质量。
质能方程告诉了我们一件很重要的事:能量即质量,质量即能量。它们是同一事物的两种表现形式,并且可以互相转化。把质量转化成能量的过程,释放出的能量是极其巨大的。
简单算一下就知道,光速是一个非常大的数字,3×108m/s,再平方一下,就是9×1016m2/s2。即便只有1kg的质量,全部转化成能量可以释放出9000万亿焦耳,足够烧开200亿吨水。值得一提的是,原子弹和氢弹爆炸之所以威力如此巨大,正是通过核反应(nuclear reaction)把质量转化成了能量。
光速无法超越
掌握了质能方程以后,来看看它的一个重要推论:光速是不可超越的。
当我们给一个粒子加速的时候,随着它的速度越来越快,质量也越来越大。现在不妨把质量随着速度增加而增加的公式写出来。不难发现,当速度跟光速相比很小的时候,质量的变化几乎可以忽略。但是当速度越来越接近光速,分母上的数值就越来越接近0,总质量(m,动质量)就会越来越接近无穷大(infinity)。
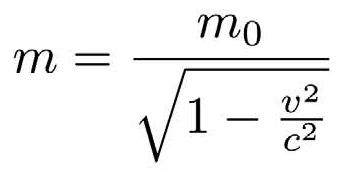
当物体的速度无限接近光速的时候,物体的总质量就会趋向于无穷大。但是很显然,宇宙中未必有无限大的能量,因此,永远不可能让一个静止时质量不为零的物体加速到光速。
这样我们就回答了最开头的问题,如果你以光速运动的时候,你的时间会静止吗?答案是,要看从什么角度来看待这个问题。根据钟慢效应,当你相对于某观察者的运动速度接近光速的时候,你的时间流逝速度,在该观察者看来是非常慢的,也许你自己掐着表,只过了一分钟,该观察者的时间可能已经过了好几年,当你越发接近光速的时候,这种效果就越发明显,当你真的达到光速的时候,你的一秒钟就等于该观察者的无限久,也就是说,如果我们假设宇宙的寿命是有限的,对于达到光速运动的你来说,你的转瞬之间,全宇宙就终结了。所以从这个意义上来说,你自己的时间确实是趋向于静止的,因为在宇宙存在的整个时间段当中,你自己看你自己的时间,几乎还没有任何流逝,宇宙就终结了,虽然你感受到自己的时间流速是正常的。
那超越光速运动会回到过去吗?质能方程说了,有质量的物体根本达不到光速,就更别说超越光速了。除非你的静止质量(restmass)也是0,这样在分子、分母都为0的情况下,整个表达式有可能给出一个有限的值。这就是光本身可以达到光速的原因,因为光子(photon)没有静止质量,它运动起来的速度必须是光速。
由光速不变原理,我们推论出了很多神奇的效应。比如,钟慢效应:运动越快,时间流逝的速度越慢;尺缩效应:运动越快,长度越短;还有运动越快,质量越大。通过这些结论,可以直接推导出爱因斯坦的质能方程E=mc2。它告诉我们,能量和质量是一回事,是同一事物的两面,并且任何物体的运动速度都无法超越光速。
相对论还告诉我们,时间和空间不是相互独立,而是相互关联的,运动状态决定了时间流逝的状态。相对论揭示了在我们这个宇宙中,一切物理观测结果都要指明是相对于哪个观察者而言的。
