广义相对论的验证及应用
第一节 水星进动问题
等效原理
广义相对论的核心原理——等效原理说的是,引力的效果与加速度的效果是等效的。
你在一个封闭系统中做各种物理实验的时候,无法通过实验结果来判断自己究竟是受到了一个天体引力的作用,还是处在一艘正在加速运动的飞船中。同样,当周围没有引力场的时候,你同样无法判断自己是处在太空中完全不受力,还是处在引力场中的自由落体状态。
从等效原理出发,我们能够沿着爱因斯坦的思想得出一个结论:引力并非一个真实的力,它体现为时空的扭曲。任何物体,甚至包括光,置身于引力场中的时候,它们的运动状态都会发生改变。
譬如天体会进行天体运动,光经过引力场的时候,会在引力场的作用下弯曲。但是这些运动状态的改变和轨迹的弯曲,并非因为力的作用,而是因为时空的扭曲。
又譬如在地球轨道上运动的宇航员围绕地球做圆周运动,按理来说,他应该有受到力的感觉,但是恰恰相反,他的感受是自己处在完全失重状态。这是因为他的时空由于引力的缘故被扭曲了,他觉得自己在走直线,但本质上是他的直线所处的时空被扭曲了。
广义相对论如此神奇,它具体有什么实验上的证据呢?我们怎么证明广义相对论的正确性,以及它在现实生活中有没有什么应用?你会发现,其实广义相对论与我们的生活息息相关,并且在未来,广义相对论对于时空性质的认知,也许是我们做超长距离太空旅行的关键,这里说的是那种能够飞出银河系,对全宇宙进行探索的超长距离旅行。
水星进动
既然广义相对论相比于万有引力定律更准确,更贴近本质,那就要去寻找用万有引力定律无法精确计算,但用广义相对论可以精确计算的现象,这个现象就是著名的水星进动问题,也是广义相对论的第一次重要胜利。
在“极大篇”的第六章《万有引力》中,我们知道实际的天体运动轨迹应当是进动的椭圆。譬如太阳系里的行星在每完成一周的公转以后,无法精确地回到出发点,因此每转一圈,它的轨道会与之前的轨道有一定的偏差,这就是进动。
水星进动问题说的是水星围绕太阳每公转一周都会有特定的偏差,但是这个偏差非常小,要过很长时间才能看出显著的效果。根据使用万有引力定律计算得到的结果,水星的进动偏差,应该是每过100年,角度差5557.62秒(秒,角度大小的单位,角度分为度、分、秒。每一个圆周可以分为360度,每一度分为60分,每一分分为60秒)。
这里水星进动的角度差5557.62秒的意思是说,100年以后新的椭圆轨道长轴跟100年前椭圆轨道的长轴存在一个夹角,换算成度的话,差不多是1.5度。但为了精确,我们还是用秒来表示。
可是天文观测发现水星进动角度并非是100年5557.62秒,而是5600.73秒,也就是观测值比用万有引力定律计算出来的理论值要多43.11秒。
为什么我们研究的是水星进动,而不是其他天体的进动呢?
原则上,其他天体的进动用牛顿定律去算也有这个问题,但是其他天体离太阳远,进动的现象不明显,偏差不大。八大行星之中水星离太阳最近,公转周期短(水星的公转周期只有大概88个地球日)。在单位时间内,公转快的天体,能够完成的圈数就多,每完成一圈,就会偏一些。所以完成圈数多,偏的效果就明显,所以我们研究的是水星的进动。
一开始,物理学家们想了很多办法来解释这个问题,有人考虑电磁相互作用,有人考虑太空尘埃的阻力,甚至大家觉得水星周围可能有一个天体一直没被发现,所以影响了它的运动。
但是后来这些都被证明是错的,人们花了很多工夫去寻找这个影响水星运动但是没有被发现的天体,却一无所获。后来终于有人质疑,是不是牛顿的万有引力定律出了问题?可能引力不是和距离的平方成反比例(万有引力跟距离的关系不是r2,而是跟2有偏差)。但是这样去计算一下会发现,如果真的要解释这43.11秒的极小误差,2要变成2.15,这怎么都不像是个符合物理学原理的结果。
从物理直觉上,这么基础的定律不太可能是这样一个不规则的数字,因为物理学家们多多少少都有一个信念:宇宙万物的规律,应当是简洁而优美的。
直到有了广义相对论,通过广义相对论的方程式去计算水星进动问题,发现水星每100年进动的角度,比牛顿算出来的确实多了43.07秒。这就跟实验观测的结果非常接近了,几乎可以说是完全吻合。这样一来,就从理论层面验证了广义相对论的适用性。
不管万有引力定律从物理学本质上是否正确,在计算上,尺度一旦扩大,它就变得不够精确了。这其实说明,一切科学理论都有自己的边界。
严格意义上,我们不能简单地说某个科学理论的对错与否,判断科学理论对错的依据,其实就是在一定边界内,它是否能够精确地解释和预测现象,因此,我们并非否定了万有引力定律,只能说它在大尺度的情况下已经失效。广义相对论目前看来在太阳系范围内十分精确,但在更大的尺度下也有失效的可能。就比方说在“极大篇”的第五章《宇宙里有什么》中提到的暗物质,单纯用广义相对论也无法解释。
第二节 引力透镜(gravitational len)
还有一个验证广义相对论的办法,就是从最基本的推论出发,看看广义相对论预言的物理现象能否被观察到。广义相对论研究的是大尺度问题,要观察也应该是去宇宙里观察,这就来到了天文观测的领域。
天文观测,粗略来讲可以理解为观星。这里的观星,其实都是看各种天体上发出的光。因此从观测的角度来说,如果要检验广义相对论的正确性,最直观的就是去验证光是否真的会在引力场的作用下弯曲。
根据这一预言,我们能够预想出,宇宙中的天体应该会有一种现象,叫引力透镜。先说说透镜,生活中能见到很多透镜,譬如说近视眼镜的镜片,就是凹透镜;远视眼镜、老花眼镜的镜片,是凸透镜。
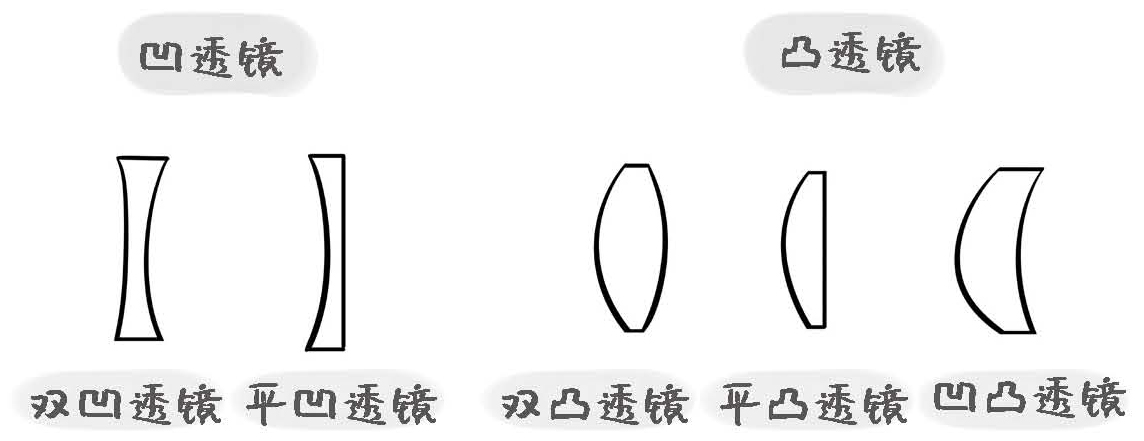
图8-1 凹透镜和凸透镜
透镜其实就是厚薄渐变的透明材料,可以是玻璃,也可以是树脂,它的功能就是弯折光,光射进去会改变方向。引力场的作用也是让光的传播路径弯曲,因此我们借用了透镜的概念。
引力透镜也是广义相对论所预言的一种天体物理现象,我们可以来看一个引力透镜的设置。比方说,有一个天体质量特别大,光经过它周围的时候会发生明显的弯曲。假设在这个大天体的背后有一些发光的天体,正常情况下,如果我们从这个大天体的正面去观察,由于发光天体被大天体挡住了,原则上是看不见的。但因为大天体的质量非常大,发光天体所发出的光经过它的边缘时会被弯曲。这种弯曲是一种吸引式的弯曲,也就是本来要向上走的光,会被大天体的引力场给拽下来往前走。可以想象,如果大天体的质量大到一定程度,即便发光天体本身被大天体遮挡了,我们也依然可以从大天体正面看到这个发光天体的光。并且由于天体是球形,所以每个方向的光发生的弯曲应该是一样的。如果大天体背后的发光天体也是球形,通过这种大天体对于光的弯曲作用,我们应该能够看到一个发光的环。
如果大天体背后的发光天体不止一个,可以预想大天体背后的光都会发生弯曲。这样一来,我们会看到大天体周围的图像都是经过扭曲的,看上去不像正常的宇宙景象,就像在Photoshop软件中经过了液化处理的图像。这就好比你通过一个放大镜去看物体,物体的形象会被扭曲一样,这就是引力透镜。黑洞,就是这样一种具备如此大质量和如此强引力场的天体。
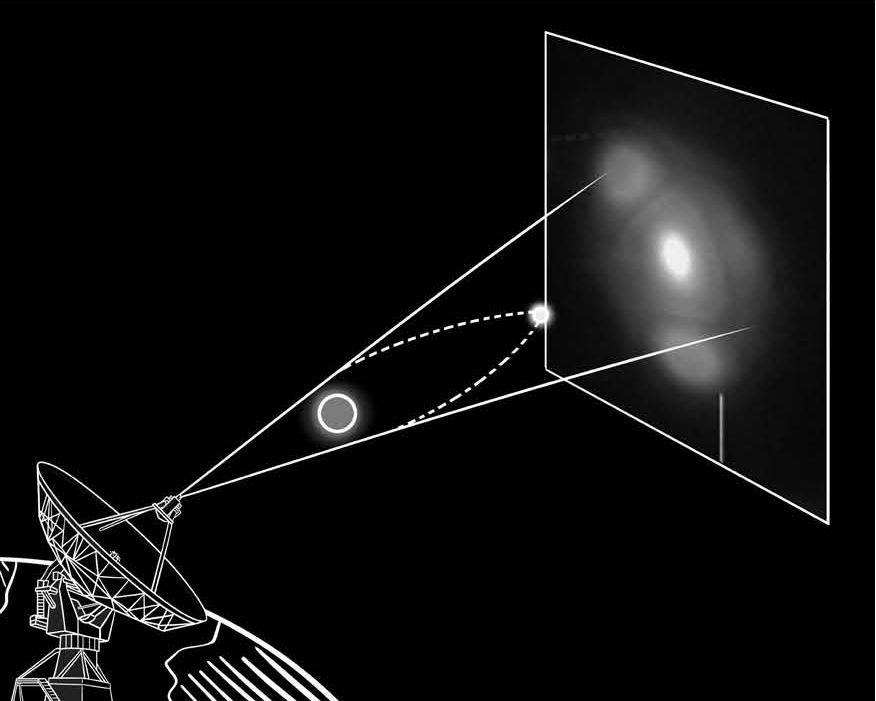
图8-2 引力透镜的“透视”效果
如果真的有个黑洞在宇宙中,我们透过黑洞看到的它周围的景象应当是被扭曲的,有很多科幻片里也做出了这样的效果图。
黑洞是引力极强的天体,这种强引力天体产生的引力透镜的现象,叫作强引力透镜。但黑洞是很罕见的,科学家也只是在2019年才第一次拍到了黑洞的照片。
在大部分情况下,没有那么多具有强引力的天体,但引力透镜的现象无处不在,只是效果明显不同。同样地,任何一个普通的天体,原则上都可以充当引力透镜。我们可以来考虑这样一个设置,譬如有一个天体,这个天体的引力还算可以,虽然没有黑洞那么强,但也比较可观。在这个天体的背后有另外一个发光天体发出的光,刚好擦着这个充当透镜的天体的边缘穿过,能够被天体前方的观察者看到。
发光天体是有一定大小的,它发出的光不是一条单一光,而是有粗细的光束。这个光束下方的光,在擦过透镜天体的时候,相比于上方的光更加接近透镜天体的球心。下方的光感受的引力场的强度比上方的光要强,下方的光在引力场中弯曲的程度更强。因此,观察者看到的这束光,比光在不受引力场影响的时候要大。发光天体的形象被放大了,这也是引力透镜的效果。

图8-3 黑洞引力场的时空扭曲
根据广义相对论的推理,引力透镜的效果是必然的。但是这样就真的证明了广义相对论的正确性了吗?答案是未必。
我们通过爱因斯坦的狭义相对论知道,能量和质量是等价的。一束光既然有能量,那么它也就有相应的质量,有质量的物体在通过引力场的过程中,会受到引力的影响而改变运行路线。水星进动和引力透镜只能说是给出了广义相对论没有错误的验证,但并非只有广义相对论能解释引力透镜和水星进动问题。广义相对论的铁证,其实是近年才被发现的,那就是引力波。
第三节 引力波
水星进动问题和引力透镜的效果,虽然是广义相对论能够解释以及预言的现象,但是这两种现象都并非只有广义相对论可以解释,它们只能说是验证了广义相对论在这两个问题上没有破溃,是属于广义相对论边界范围内的问题。同样地,用万有引力定律来解释,如果不要求那么高的精确度,也是可行的。相比之下,只能够用广义相对论去解释的问题,就是引力波。
时空的涟漪——引力波
什么是引力波呢?顾名思义,就是引力的波动。但是光看名字是不够准确理解的,引力波应该被理解为时空扭曲程度的周期性变化,这一变化的信息以波动形式传递,它是时空曲率的波动。
我们依然可以用解释时空扭曲的案例来解释引力波。一张桌布撑开,在上面放一个铅球,桌布会在铅球的重力作用下凹陷,这个凹陷是固定的。我们现在想象,再扔一个铅球在这张桌布上,两个铅球在桌布上滚来滚去,整张桌布就会跟着抖动起来。铅球把桌布压得越深,就对应广义相对论中天体质量越大,两个铅球的运动就好比时空中质量的分布在发生显著变化,就会产生越强烈的时空扭曲的变化。这种变化向外传播出去,就形成了引力波。
引力波的传播速度恰好等于光速,这都是广义相对论的推理结果。在目前所有的科学理论中,只有广义相对论预言了引力波的存在,所以只要能够探测到引力波,就证明了广义相对论的解释力比其他理论要强。
引力波如何探测?
引力波是在2015年9月,被美国一个叫LIGO的超大实验装置第一次探测到的。LIGO是个缩写,全名是Laser Interferometer Gravitational-Wave Observatory,意思是激光干涉仪引力波探测器。它的原理跟我们在“极快篇”的第一章《狭义相对论》讲解的迈克耳孙-莫雷实验的原理类似。
迈克耳孙-莫雷实验的目的是去寻找以太这种假想中的物质,最后证明以太并不存在,但是它的实验方法却是十分精妙的。迈克耳孙-莫雷实验获得了1907年的诺贝尔物理学奖,LIGO也因为发现了引力波,于2017年获得了诺贝尔物理学奖。
迈克耳孙干涉仪的结构是左边一束光射出,打到分光镜上,分成一束向右的光以及一束向上的光。两束光都经过相同的距离后碰到一面镜子再反射回来,最终汇聚在下方的探测器形成干涉条纹。
LIGO的结构跟迈克耳孙干涉仪的实验装置几乎完全相同,也是一束激光(laser)分为两束,让这两束激光完全垂直,然后再反弹回来,汇聚到探测器上形成干涉条纹。但是LIGO跟迈克耳孙干涉仪比起来,就大太多了。迈克耳孙干涉仪的两条光路的长度大概是几十厘米,而LIGO的两条相互垂直的光路的长度达到了4km。两束激光被分出去再汇聚回来,各自都要经过8km的路程。
如果有引力波经过地球,由于引力波本质上是时空的扭曲,被引力波扫过的地方时空都会发生扭曲,那么这两条光路所处空间发生的扭曲程度大概率也是不一样的。两条本来都是4km长的光路,在引力波的作用下,长度都会发生变化,并且由于它们所在的空间被扭曲的程度不一样,所以它们长度的变化肯定也不一样。
因此,两束激光在引力波经过的时候,各自走过的路程会不一样,当它们到达探测器的时候,就会有时间差。这个时间差会让它们的干涉情况发生变化,并被探测器捕捉到。这就是LIGO如何探测到引力波的原理。
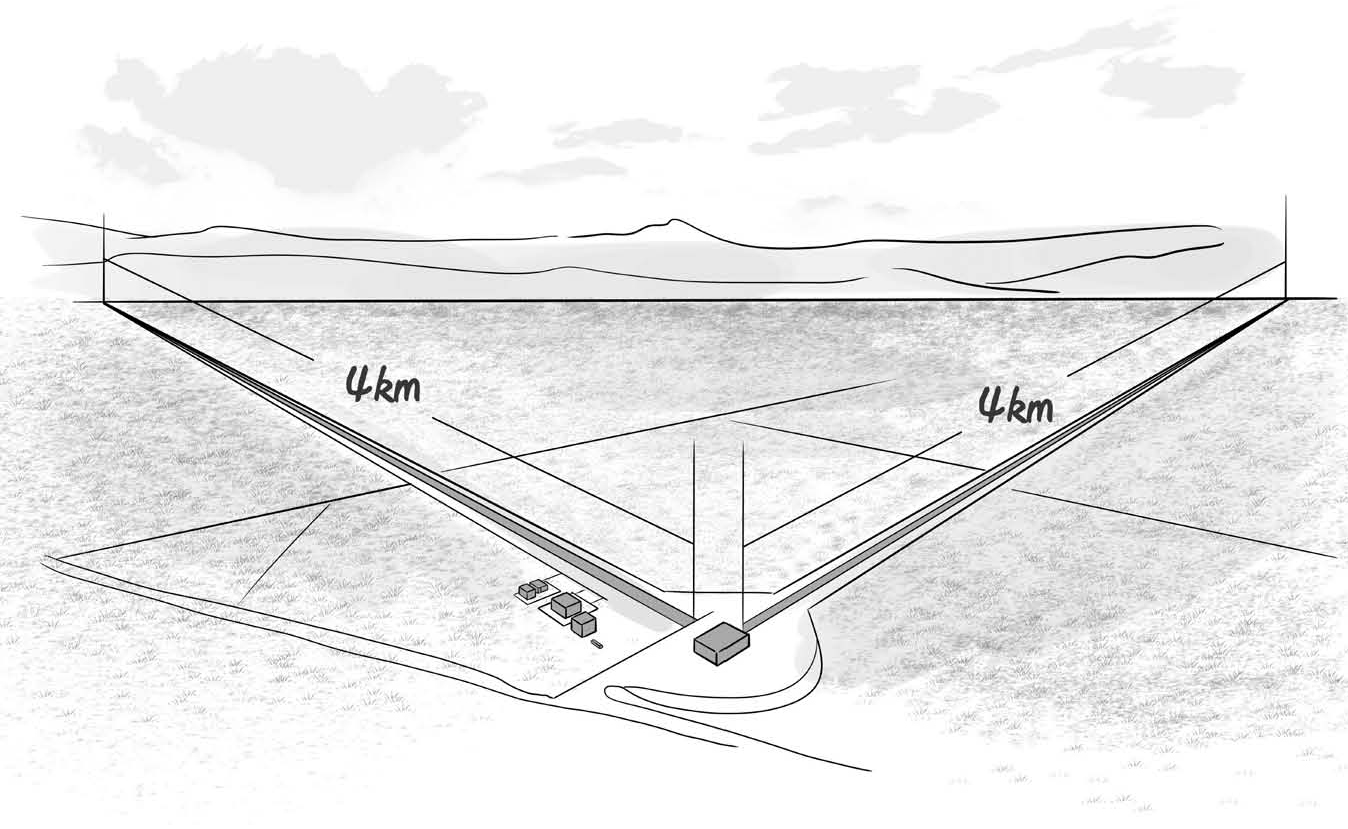
图8-4 LIGO激光干涉引力波探测器
LIGO项目研究工作其实在20世纪60年代就开始了,由美国科学家主导,实验室在全世界各地都有。但是由于实验仪器一开始精度没有那么高,且几十年过去都没有探测到任何引力波,所以21世纪初的时候经历过一段时间的停滞,毕竟这个项目耗资非常大。直到2015年9月,引力波终于第一次被发现。这次引力波源自13亿光年以外的两颗30倍太阳质量量级的黑洞融合成的一个单一黑洞。
为什么之前探测不到引力波?
为什么要等那么久才能探测到引力波呢?有两个主要原因:
(1)实验仪器和实验手段需要不断进步;
(2)最主要的原因,引力波实在是超乎想象的弱。
引力是一种极其弱的力。至于引力有多弱,我们在“极大篇”的第六章《万有引力》中曾经举过一个例子,一个小铁钉落地是因为地球对它的万有引力,但是它可以很轻松地被一个小磁铁吸起来,一个小磁铁提供的磁力就可以打败由整个地球提供的引力。甚至可以粗略地认为,地球的体积是小磁铁的多少倍,引力就比磁力弱多少倍。
由此可见,要探测到引力波是极其困难的,这也是为什么LIGO的两条光路要建得那么长。引力波太弱了,即便它传了过来,它能让光路长度改变的比例也非常小。因此我们要让光路尽量长,足够长的光路,即便改变的比例十分小,也足够让两束光的时间差变得可测。就是因为引力波太弱,所以整个LIGO的仪器设置都必须用激光调节至极其精确,保证实验误差不会大到影响对引力波的观测。
那为什么2015年9月又测到引力波了呢?这是因为13亿光年以外发生了天体物理上的大事件,两个30倍太阳质量量级的黑洞合并到了一起,它们质量足够大,引力足够强,而且从相互靠近到融合,是一个极其剧烈的变化过程。这种合并会对其周围的时空产生翻天覆地的扰动,形成的足够强烈的引力波,经过了13亿年的时间传到地球上。所以,引力波的探测也需要运气,这种天体大事件也不是经常会发生的。
引力波的发现和证实,圆满地证明了广义相对论的正确性。因为引力波的现象是完全被广义相对论所预言的,它并不能由牛顿定律解释。
第四节 全球定位系统
可以说,如果没有广义相对论,我们现代生活中需要定位的服务都无法达成,更不要说军事领域的精确制导了,全球定位系统无法做到现在的精准度。
如何确定一个事件的位置
首先要明确,在地球上确定一个位置需要四个坐标,分别是三个空间坐标和一个时间坐标。
我们在“极快篇”的第一章《狭义相对论》里就已经谈到过,三个空间坐标在地球上对应的是经度、纬度以及海拔。我们的手机通过卫星定位定准一个位置,靠的就是这四个坐标。
全球定位系统的工作原理
全球定位系统的工作原理,就是通过至少四颗卫星,来确定四个坐标。美国的全球定位系统(GPS),是在地球的轨道中布置24颗卫星。之所以要有24颗,为的是在地球的任何一个角落,都至少能同时接收到4颗卫星的信号(当然,24颗卫星不是唯一的选择,卫星的数量多多益善,只是24颗从实用角度可以充分满足需求,且其中3颗是备用卫星)。
这24颗卫星的位置是已知的,并且在这24颗卫星中,都有铯原子钟。铯原子钟计时的准确度极高,高到什么程度?每过2000万年,误差只有1s。24颗卫星中的时钟都是用铯原子钟校准的,同时它们与地球上的时钟也是同步的。
这些卫星都在做一件事,就是向外广播自己的时钟时刻以及目前的坐标位置,这些信号是在全球范围内都可以接收到的。你的手机如果想定位,要至少接收4颗卫星所广播的信息。
接收到信息之后,手机就立刻与自己的时钟进行比对,算出这几个信号所携带的时间信息与自身时钟的时间差,再结合卫星的位置信息,根据光速不变原理,就可以算出自己和每颗卫星之间的距离。
不管卫星和手机是否在移动,它们测出的光速都是一个恒定的值,所以要测量手机跟卫星的距离,只要将时间差乘以光速就可以了。
再以每颗卫星的球心到手机的距离为半径,就可以在空间中画出一个球形。几个球形一交叠,就能算出来自己的位置,这就是全球定位系统的工作原理。3颗卫星用来确定位置信息,1颗卫星用来校准时间信息。
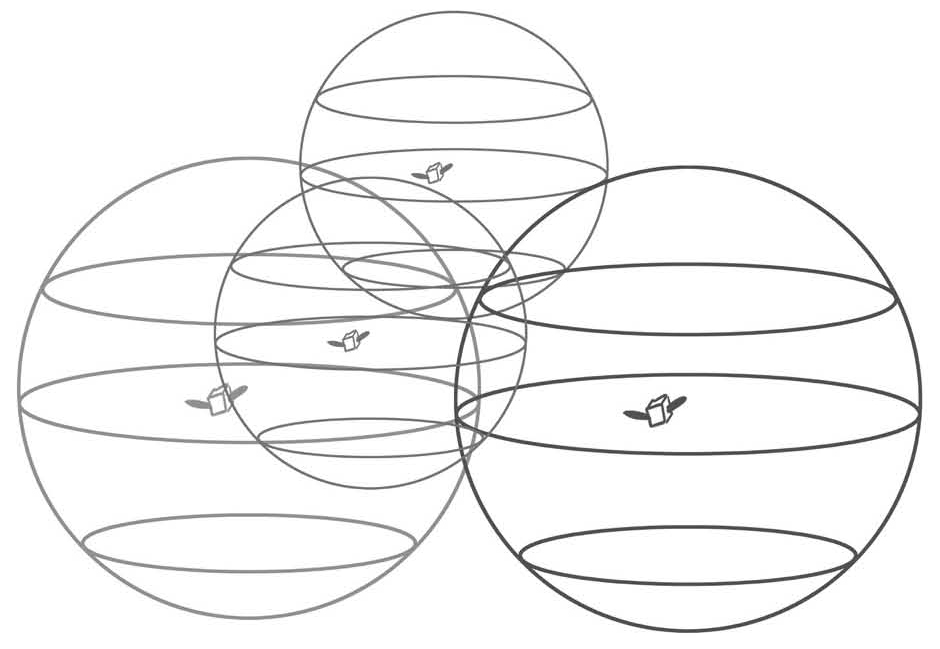
图8-5 全球定位系统的工作原理
广义相对论的修正
广义相对论在全球定位系统里的作用是什么呢?我们计算手机与卫星的位置,用的是光速乘以时间差,并且默认电磁波信号的路径是直线。但是根据广义相对论,电磁波在地球的引力场中走的不是直线,而是曲线。
在这种情况下,如果不把广义相对论的影响算进去,算出来的位置就会有误差,这个误差还不小,大约会在100m以上。100m的误差,在纽约曼哈顿就已经相差两条街了,不论是外卖、网约车都无法进行精准的定位,更不要说精度到了厘米数量级的军用卫星定位了。如果没有广义相对论,很难想象我们的生活会变成什么样。所以说,广义相对论不光是一个深刻的高级理论,也是我们现代生活中必不可少的理论工具。
第五节 曲率飞船(Warp Drive)
我们在科幻电影,比如《星球大战》和《星际迷航》中,经常会看到一些超光速飞行的宇宙飞船,而且这些宇宙飞船,大多叫曲率飞船。为什么它们的名字都一样?因为这些飞船的运行原理不是瞎编的,它确实有一定的理论基础,这个理论就是广义相对论。
墨西哥有一位理论物理学家叫米盖尔·阿库别耶(MiguelAlcubierre),1994年,他给出了一种假想中的宇宙飞船。根据他的设计,这种宇宙飞船可以以超光速运行,但并不违背相对论中超光速无法实现的限制。
为什么宇宙膨胀可以超光速?
先来回顾一下哈勃定律,哈勃定律说一个天体远离我们的速度正比于它与我们的距离,这个比例叫作哈勃常数,大小是70km/(s·Mpc)。按照这个公式算一算,那些离我们非常远的天体,比方说几十亿、上百亿光年以外的天体,会以超过光速的速度远离我们,也就是说宇宙的整体膨胀速度是超过光速的。但是根据爱因斯坦的狭义相对论,不是任何东西运动的速度都不能超过光速吗?
这里要明确,宇宙的超光速膨胀并不能理解为天体的运动速度超过了光速,而是宇宙时空的膨胀速度超过了光速。爱因斯坦的相对论,说的是一个物体相对于观察者来说的运动速度不能超过光速。宇宙时空的膨胀,应当理解为时空本身的膨胀。一个天体远离我们,并不是它相对于我们在运动,而是时空本身在把这个天体运走。就好比一个膨胀的气球,气球上的点代表了天体,因为气球的膨胀,天体看上去在远离我们,但实际上,气球上的每个点并没有相对于它原来的位置有所运动。因此,此处并没有违背狭义相对论。
曲率飞船的基本原理
有了这个认知,我们就能够从原理上设计超光速的宇宙飞船了。原理说起来也不难,就是让飞船在它的前方制造一个收缩的时空。譬如通过极高的能量密度,让飞船前方的时空收缩,再用一定手段让飞船后方的时空膨胀。这样的话,飞船就置身于一个前方收缩、后方膨胀的时空区域当中。这样,整个飞船以及它周围的时空,都会因为前方的收缩和后方的膨胀而往前挪动一个位置,这种飞船就叫曲率飞船。这里要注意,飞船相对于它的空间并未发生移动,而是飞船连同周围的空间整体向前挪动了一些。
原则上,只要能量足够大,飞船的整体运动速度就可以无限制地提升,然而因为飞船相对于自己周围的空间并没有运动,因此完全不违背狭义相对论。
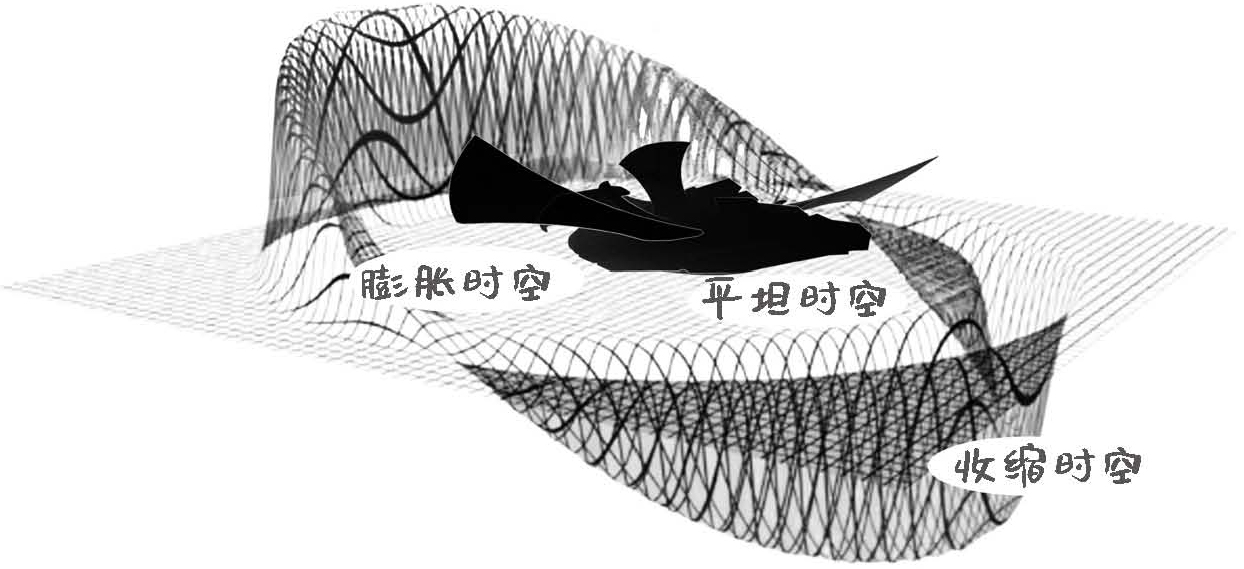
图8-6 曲率飞船的原理
这个过程就好像我有一块橡皮泥,上面有一只蜗牛,我可以把蜗牛前方的橡皮泥挤压一些,后方的橡皮泥拉伸一些,这样蜗牛连同它周围的橡皮泥都被往前移动了一些,但是蜗牛相对于自己下方的橡皮泥根本没有运动。
你如果注意观察就会发现,很多科幻电影里面考虑得还是非常到位的。飞船在正常飞行的时候,比方遭遇了一些太空战的飞行场景,这些飞船里的人员都会晃来晃去,因为飞船在不断改变航向。但是一旦用上曲率加速,飞船里的人站得反而很稳,他们瞬移的时候,完全不会因为飞船的加速减速而前后摇摆,这恰恰是曲率飞船的好处,因为对于飞船来说,尽管它的坐标发生了改变,但是实际上并没有运动。
负能量
这里有个关键问题,让时空收缩还是相对好办的,质量的效果就是让它周围的时空收缩,并且能量和质量是等价的。因此,只需要在飞船前方制造足够强的能量密度,原则上就能获得可观的时空收缩。但是后方的时空膨胀就不好办了,因为所有我们能够大规模制造出来的能量,都是正能量,我们只能让时空收缩。但是要让时空膨胀的话该怎么办呢?
一个可能的答案是负能量,也就是数值为负的能量,比零还要小。负能量涉及比较深的量子力学的知识,我们将在“极小篇”做特别的介绍,负能量可以被理解为比真空的能量状态更低的能量。这将会涉及量子力学的一种特殊效应——卡西米尔效应(Casimir effect)。卡西米尔效应理论上能帮我们获得负能量,但是这种负能量实在少得可怜。因此,如果要制造一艘曲率飞船,负能量的收集将会是巨大的挑战。
