固体物理
第一节 能带结构(energy bandstructure)
既然材料的性质本质上是由原子的微观属性结合而成,那么用量子力学才能进行最贴近本质的分析。
固体内部的原子布局
要研究材料的量子性质,就需要对研究对象做量子场景的描述。我们在“极小篇”已经对原子的量子场景做了比较清楚的分析,原子的中心是原子核,周围是围绕原子核运动的电子。由于原子核远远重于电子,是电子质量的几千倍,甚至几万倍,所以我们将原子核当成不动的,它处在原子中心,只是贡献了一个来自中心的电势能给电子。要想描述电子的运动,用薛定谔方程来描述电子的概率波即可。这是单个原子的量子力学图景,是相对简单的。但是对于固体,情况要复杂得多。
固体中众多原子排列在一块儿,对于一个电子,它感受到的是众多原子提供的电势能。我们可以用薛定谔方程去描述它的波函数,但这时电子受到的影响要复杂得多。
简单算一下,固体中的原子核与电子之间有三组相互作用。首先,原子核之间有电磁相互作用,电子和电子之间也有相互作用,每个电子还会感受到所有原子核的电磁力。三组作用交叠在一起,是一个极其复杂的系统,必须做一定近似来简化模型。
首先,可以忽略原子核之间的相互作用。原子核的位置相对固定,相比之下,电子的运动则自由得多,比如金属里有很多自由运动的电子,相对于电子来说原子核几乎不动,虽然不同原子的原子核之间有相互作用,导致二者的位置发生变化,让周围的电子获得不同的电势能,但是这种变化相对于活跃的电子来说不显著,它只会少量影响电子的运动。
其次,可以忽略电子和电子之间的相互作用。我们知道原子之间的距离很大,电子在固体里的运动实际上非常自由,这里可以借用“极热篇”中分析理想气体的模型时说到的,电子之间即便有相互作用,其影响也是微弱的,不会定性地影响电子的行为。当然,这个假设只在特定情况下成立,确实有不少材料[比如莫特绝缘体(Mott insulator)]中电子间的相互作用非常强烈,不能被忽略。但是这里为了方便分析,就先不去研究莫特绝缘体这样的材料,而是着眼于一般的材料。如果考虑电子和电子之间的相互作用,其实对应于物理学中一个重要的研究课题——强关联系统,这里的强关联指的就是电子和电子之间的相互作用强到不能忽略。
如此一来,就只需要考虑单一电子与所有原子核之间的电磁相互作用。我们对晶体中的电子运动尤其感兴趣,晶体内部的原子呈规律的几何形状排列。比如氯化钠的内部结构就是六面体,基本是个正方体,每个钠原子被6个氯原子包围,每个氯原子又被6个钠原子包围。晶体结构满足了我们的第一个近似假设,即原子的原子核可以被视为静止,目前只需关心晶体内的电子如何运动。
这样一来,我们对于晶体的初步量子物理图景就比较清楚了,就是一堆原子组成了一个三维的阵列,这个阵列具有规则的几何形状,然后考虑一个带负电的电子会在这个阵列当中如何运动,它的波函数满足整个阵列的薛定谔方程。
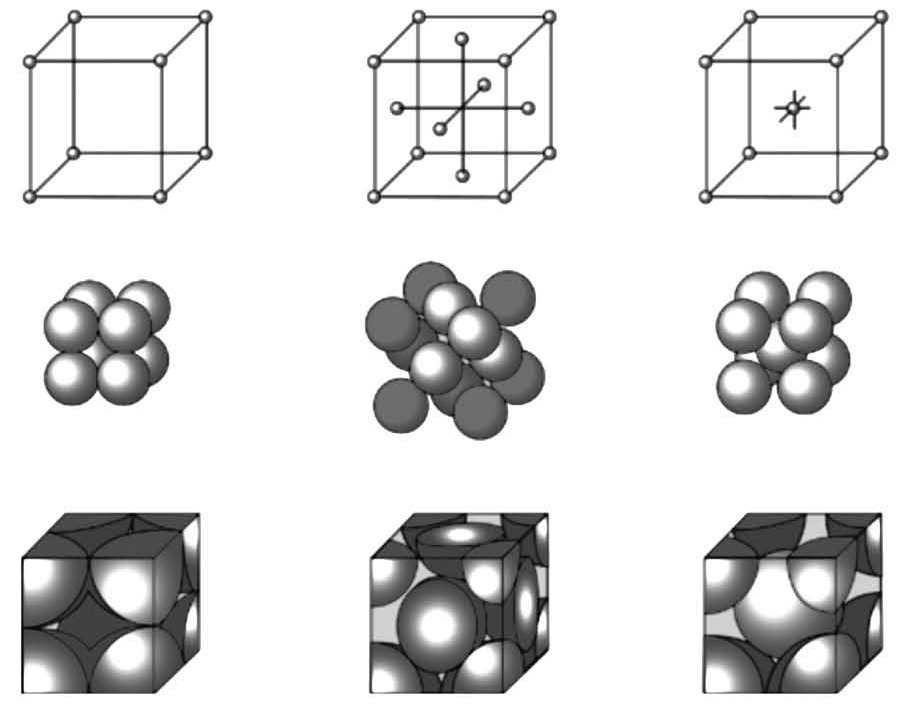
图19-1 三种不同类型的晶体结构
按理来说,只要去解这个阵列的薛定谔方程,就能够明白晶体中电子的波函数的规律,但在“硬解”方程之前,可以先做一番物理直觉上的分析。
单个原子内部是量子化的电子,电子的能量是量子化的,这些能量等级是离散、不连续的,每个能量等级之间有一个间隔。
多原子的能级
单原子中电子受到一个原子核的影响,就出现了能量量子化的特点。这时再多来一个原子核,比如让电子围绕两个分开一定距离的原子核运动,能量的量子化会消失吗?
直觉上应该是不会的,对于电子来说,无非是原子核的正电荷的分布发生了一些定量的变化,这种能量分级的量子特性理应不会消失。那么,三个原子核怎么样?四个?N 个?形成阵列?这种能量量子化的特点会消失吗?直觉上应该不会消失,但是一定会对电子的能级的具体形态产生影响。

图19-2 电子在晶体中的波函数形态,总体呈正弦波形态,局部偏离正弦波
布洛赫定理(Bloch theorem)
物理直觉我们有了,也就是晶体中电子的能量应该是量子化的,能级之间有间隔,但是间隔的大小以及电子的波函数的形态,会受原子核阵列的定量影响。有了这个猜想,再看如果真的解一个阵列中电子的薛定谔方程会怎么样。这就引出了固体物理学当中一条极其重要的定理——布洛赫定理。
布洛赫(Felix Bloch)是一位瑞士物理学家,他就是在解阵列中电子的薛定谔方程的过程中,得出了布洛赫定理。这条定理说的就是在一个做周期性变化的势能场中,薛定谔方程的解的形式是一个正弦波叠加一些局部的变化。也就是说在阵列当中,电子的波函数的形态大致上是一列正弦波,但是有一些局部变化。
能带结构
有了布洛赫定理,通过薛定谔方程解出来的波函数,叫布洛赫波。相应地,不同的布洛赫波对应了不同的能量状态,这些能量的解,验证了我们之前的物理直觉,也就是电子在晶体中的能量依然是量子化的。周期性阵列对于电子能量的量子化规律有修正,但是相对复杂。原来单个原子中电子的不同能量叫能级,到了晶体,能级就变成了能量带,简称能带(energy band),单个原子中电子的能级是一个数值,而晶体中电子的能存在的能量是一个能量范围,一个区域就是一条能带。
电子可以处在不同的能带,一条能带里电子的能量是连续的(当我们把材料的大小想象成无穷大的话,能带里的能量是连续的,但是真实情况下,一块材料总是有大小的,所以,比较安全的说法是,能带里电子的能量是接近连续的),但是不同的能带之间有一个能量间隔,这个间隔叫作能隙(energy gap)。
原来单个原子中的能级是量子化的,每个能级的数值是一个单一的值,在阵列结构中,能量间隔还在,但是能级被“拉宽”成能量带。这条能量带对应的不再是一个能量值,而是一个范围内连续的能量值,但是整体量子化的能隙还是存在的。
如何理解电子在一个能量带里能量是连续的呢?当一个电子在能量带里取到不同的、连续的能量时,对应于什么运动状态?这就要回到布洛赫定理。
布洛赫定理说的是,电子的波函数总体来说是正弦波,只是局部有修正。那么答案就很容易理解了,那就是在一条能带里,不同的能量对应于电子作为一个整体正弦波的不同的波长。可以想象电子的波函数在晶体里大致还是像电磁波那样的正弦波,但是它的能量获得了修正。
不同波长的波,对应于不同的能量高低。
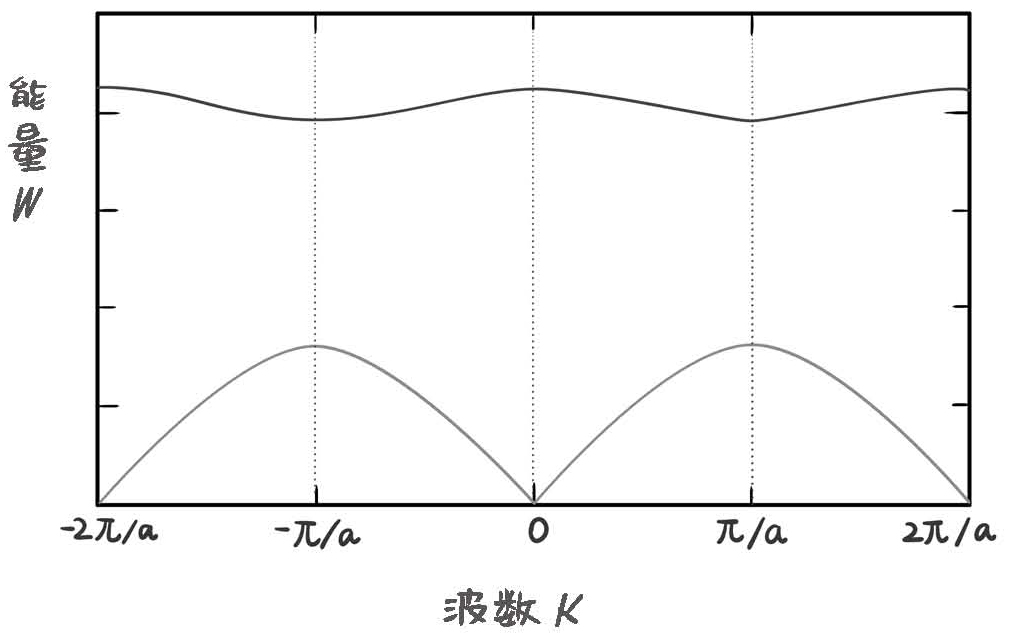
图19-3 能带结构示意图
如图19-3所示,横坐标是不同电子波函数的波数,波数就是单位长度内波的个数,用字母k表示(k=2π/λ,λ是波长),波数反比于波长,波长越短,波数越多。波数是矢量,它的方向代表了波的传播方向。不同方向以及不同波数的波,对应不同的能量,这个关系叫作色散关系(dispersion relation),也就是电子的概率波的波长与能量的关系。
通过能带结构可以看到晶体的特点,那就是只有特定能量和特定波长电子的波函数可以存在,晶体结构本质上是对电子的状态进行了选择。
有了这个认知,我们对于固体量子效果的研究,就变成对固体能带结构的研究。固体的量子性质的图景,也逐渐清晰了。
第二节 导体、绝缘体、半导体
有了能带理论,再回过头来看看,什么是导体、绝缘体、半导体?什么是自由电子?这些问题都可以用能带理论统一解决,再也不用像我们上一章讲的,用一种半宏观半微观的定性方式去分析了。
什么是自由电子?
首先来讨论一下,什么是自由电子。
什么叫自由?这里对于自由的理解应该是:只要想让它动,它就能动。要让电子动,肯定要施加外力,这个外力就是电磁力。所谓的动,就是电子在电场的作用下开始移动,这里的动是定向的运动,如果不是定向运动,就不能形成电流。比如,一个电子被一个原子束缚住,加个电场它确实可以动,但是简单动一下就会被原子拽回来,这种动最后变成了一种振动,它不是定向流动,形成不了电流。
所以,自由电子应该是只要加个电场,它就能发生定向运动。这里还有一个隐含假设,就是不论加的电场有多小,它都能定向运动。可能加的电场小一点儿,它动得会慢一些,但是不改变它能动的事实。自由电子应该更准确地被描述为:不论加多小的电场,只要有个电场,它就能开始定向运动。
尽管有电阻存在,但只要一直加电场,它就能维持定向流动。电场小,相当于电压小,电压小电流就小,电流小的意义其实就是单位时间内通过的电子的数量少,对应的就是电子运动速度慢。
到这里,我们再来看看用能带理论如何解释导体、绝缘体,甚至半导体。导体需要有自由电子,也就是那些只要加了电场,不管这个电场多小,都能够定向运动的电子。
什么是导体?
现在来看能带结构,首先要参考我们是如何理解原子中电子排布的,先把原子里的电子轨道解出来,然后能量从低到高,参照泡利不相容原理,每个轨道放两个电子,一层层地放上去。
那么对于晶体的能带结构,这个过程是完全一样的。从能量低的那些点开始,把一个个电子按照能量由低到高放进去。就是对着图19-3,从低到高放电子,每个放进去的电子,都有自己的波函数,这个波函数是局部有变化的正弦波,波的传播方向由能带图的波数(k)的方向决定。有k就有能量,有多少电子,就能填多高。
金属的原子最外层电子数都是不到半数填满的,在填能带图的时候,金属这类导体的电子,不能填满整条低能的能带,而是半满的。这时可以论证,这种没有被填满的能带代表了导体的能带。为什么?我们加一个电场看看有什么效果。
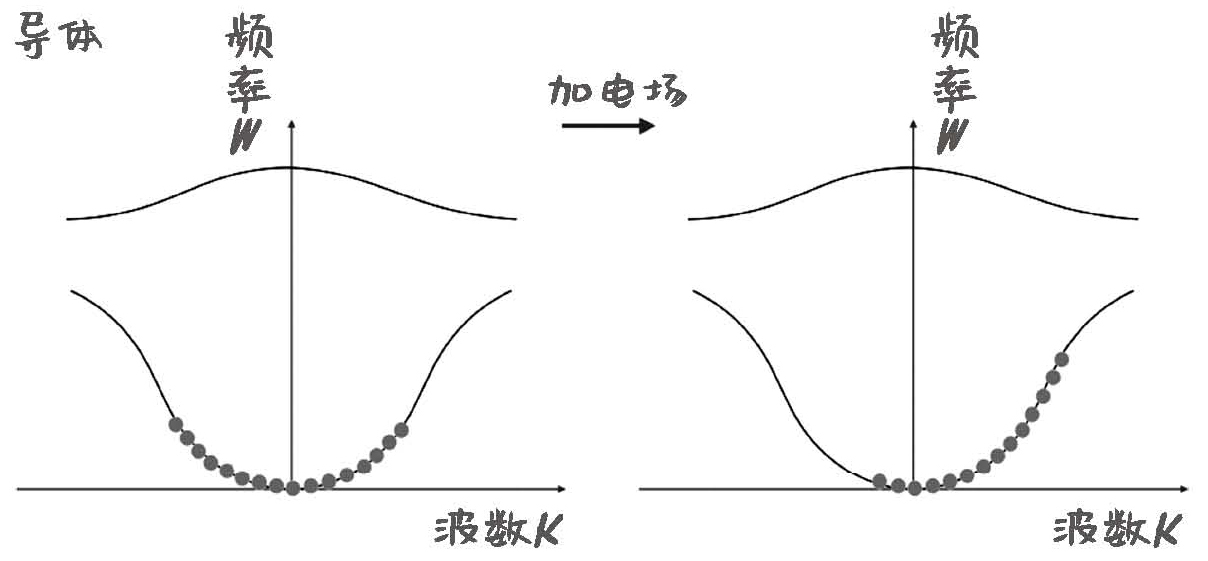
图19-4 导体能带图,电子在能带中半满
在没有电场的时候,电子的运动是杂乱的。虽然在导体里,这些电子的状态都用波函数来描述,但是各个方向的波都有,所以总体不呈现为电子的定向流动。但是加了电场就不一样了,加了电场之后,所有电子的能量都会向一个特定方向整体升高。也就是说,能带里的这些电子,都要往能量高的地方跑。
假如电场的方向,跟能带图19-4中右半边的波函数的方向一样,那么能带里这些电子的整体位置要向右移动,才能获得能量的整体升高。
恰恰因为现在的能带还不满,所以这些电子有整体向右移动的空间,加一个电场,就能让所有电子的动能都升高,原本能量低的电子可以在能带上没有被填满的地方找到空隙放下。这时,能带中的电子分布就不再左右对称了。换句话说,往能带图右边运动的电子的数量,比往左边运动的电子数量多。能带图的横坐标代表了电子波函数的运动方向,往某个方向运动的电子数量就比别的方向多,就体现为电子的定向流动,这就导电了。
什么是绝缘体?
用类似的分析方法,绝缘体也好理解了,它的原子外层轨道超过半数填满,对应到能带结构,是它的能带是被电子填满的。
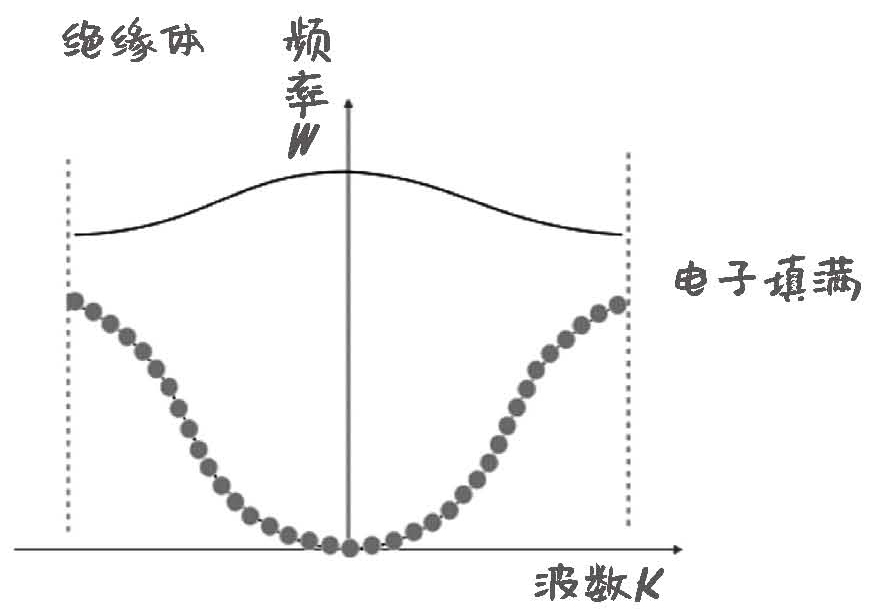
图19-5 绝缘体能带图,电子在能带中填满
根据泡利不相容原理,能带里每个点只能有一个电子,由于能带已经被填满,所以没有办法在同一条能带里让所有电子能量升高,除非跳出这条能带,往上面的能带去。但是不要忘了,上下能带之间有能隙,也就是有能量间隔。如果电场加得不够大,达不到能隙的大小,电子是没有办法跳到上一条能带去的。这种情况下,电子无法发生定向运动,这就是绝缘体。
什么是半导体?
半导体也很好理解,它是最外层电子半满的原子,比如硅。用能带理论解释起来更加直观,半导体就是能隙间隔很小的晶体。半导体的上下层能带间的能量间隔非常小,电场稍微大一点儿,电子就可以跳上去发生定向移动。
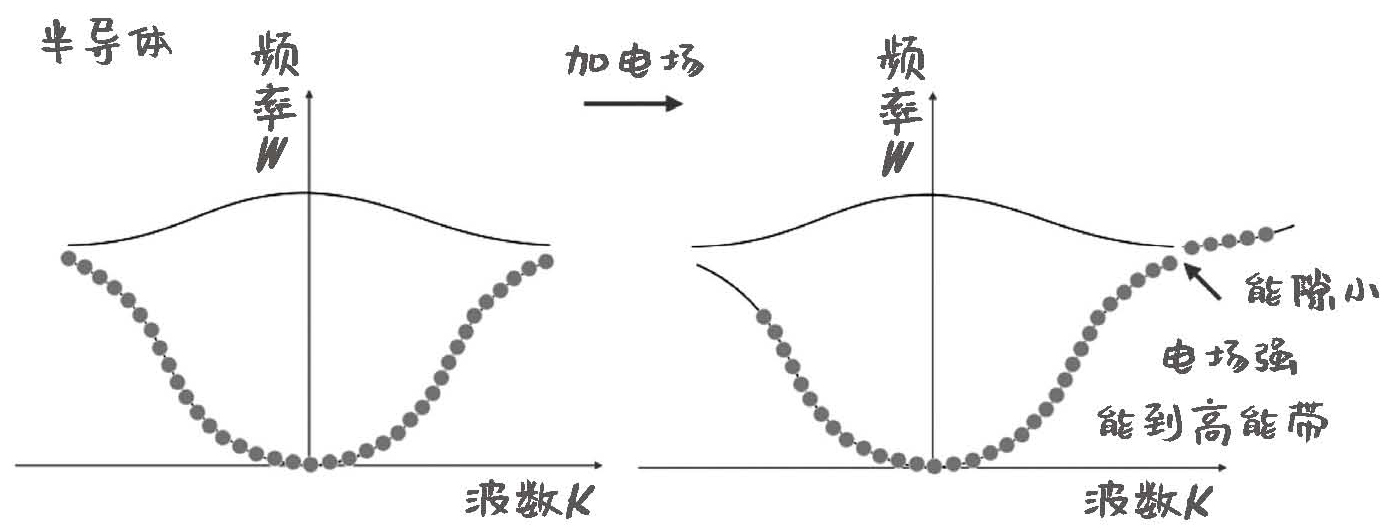
图19-6 半导体能带图,电子可以跳跃能隙
至此,我们可以发现固体物理的能带理论非常强大,我们再也不用定性地分析导体、半导体、绝缘体,而是用一套统一的理论体系就可以描述相关性质。
第三节 固体磁性的统合性研究方式
材料的磁性可以分为抗磁性、顺磁性和铁磁性。其中抗磁性比较简单,顺磁性和铁磁性是非常有趣的物理学现象。顺磁性和铁磁性之间有居里温度作为连接,也就是说,当固体的温度超过它的居里温度以后,就会变成顺磁性。所以,铁磁性才是最有趣的一类磁学效应。
为了研究铁磁性,以及在不同环境下(比如加磁场、温度变化)铁磁性会如何变化,我们需要像研究固体的导电性那样,建立一个简单、抽象的模型,通过研究模型,对材料的磁学性质进行更深入的了 解。
伊辛模型(Isingmodel)
简单来说,拥有铁磁性和顺磁性的材料,就是加了磁场之后,固体内部电子自旋在磁场的作用下形成定向排列,使其内部的磁场进一步加强。在磁场的作用下,固体内部的电子自旋所代表的小磁铁都倾向于整齐排列变成一个大磁铁,所以除了内部,固体周围的磁场也会加强。
铁磁体之所以会有加强磁场的特点,是因为它外层轨道中的电子,并没有以自旋相反的方式成对出现在轨道中,而是最外层的电子,一个电子占据一个轨道。它们就像自由散落在固体里的小磁铁,相互独立。一旦受到磁场的作用,这些小磁铁就听从磁场的号召,往一个方向排列,从而加强了磁场。
铁磁体的原理这样解释虽然已经相对清楚,但是我们不能只满足于解释这种现象,还要去研究它在不同物理环境下表现出来的物理规律。例如,为什么把磁场撤了,铁磁体的磁性还在,而顺磁体就不行?为什么铁磁体加热到超过居里温度就变成了顺磁体?
既然铁磁体里的电子像一个个小磁铁,那不如构造一个模型,把电子排列成阵列。在这个阵列里,我们关注电子的磁性质,也就是它们自旋方向的排列。这个模型叫伊辛模型,它是德国物理学家楞次(Emil Lenz)发明的。楞次把这个问题给了自己的学生伊辛(Ernst Ising),伊辛也是一位德国物理学家兼数学家,最早的伊辛模型就是伊辛解出来的。
要了解这个自旋阵列模型,就要看阵列里小磁铁的指向是怎样的形态:是指向同一个方向,还是完全随机,杂乱无章,抑或随着时间迅速变换方向?这些小磁铁是不是可以形成一定的图形,比如以一点为中心,所有的小磁铁排列成一个涡旋?
这个阵列不是一个静态的阵列,小磁铁会产生磁场,磁场又会影响到周围的小磁铁,它们之间存在相互作用。假设系统有温度,而温度本质上就是这些小磁铁做无规则运动,也就是说,这是一个既有自旋之间的相互作用能,又满足统计力学规律的系统,要解释它,就必须找到这个系统的行为所遵循的原则。
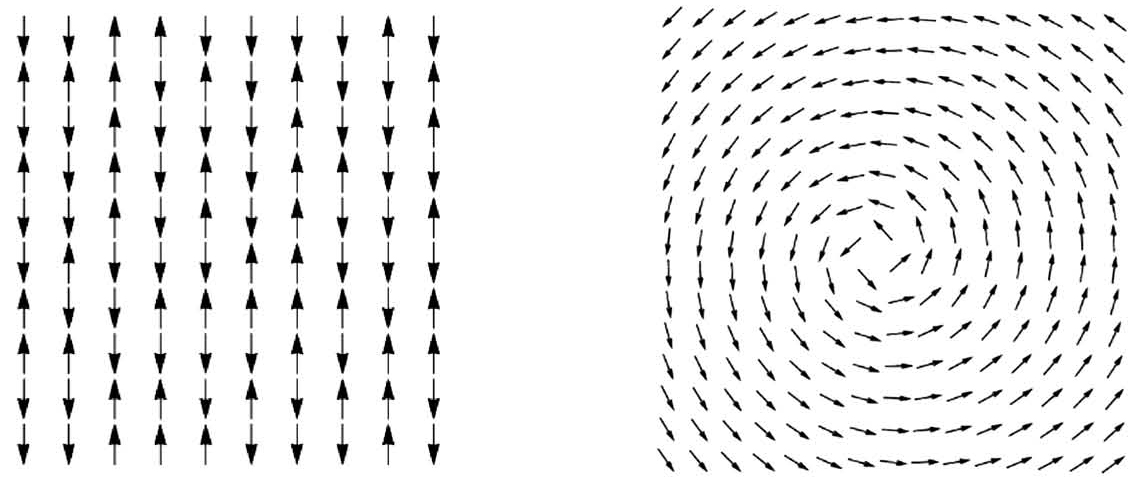
图19-7 二维伊辛模型中的电子自旋方形阵列和涡旋阵列
一个系统的稳态是其能量最低的状态。我们可以把这个系统的最低能量的状态解出来,看看什么状态下能量最小。很显然,当两个磁铁反平行放置,也就是N级对着另外一个磁铁的S级时,能量最低、最稳定。你试着把两个磁铁扔在一块儿,一定会发现它们会自发形成这种连接方式。根据能量最低原理可以得出,这个二维的伊辛方阵中,电子自旋的排布方式,应当是相邻磁铁的指向相反。
但是这个系统同时是有温度的,是一个满足统计力学规律的系统。这说明系统的状态如果是稳态,一定是熵最大的形态。熵对应于系统的混乱程度,如果所有相邻的自旋都反平行排列,这种状态是一种极其有秩序的状态,那么很明显,应当有更加混乱的状态可以增大它的熵。也就是说,能量最低原理和熵增原理在这个问题上似乎存在矛盾。
自由能(free energy)
我们忽视了一个问题:这个系统的总能量,并非只有自旋之间的磁相互作用。系统本身具有温度,有温度说明有无规则运动的热能,温度恒定的情况下,热能也是恒定的,也就是这个系统在恒温情况下拥有热能的“背景噪声”一般是无法排除的,否则这个系统就不可能具有恒定的温度。因此要降低的不只是这部分自旋之间磁相互作用的能量。这就对应了一个统计力学的概念——自由能,我们要做的是使自由能最低。
自由能可以简单理解为能量减去它的温度乘以熵,F=E-TS。在这个方程式里,F是自由能,F要达到最小,能量E则要尽量小,熵S要尽量大(TS就好像整个系统的背景噪声一样,要做到的是排除了热能的“背景噪声”以后的系统的总能量,也就是自由能是最低的)。我们的最终目标,是通过自旋的反平行趋势与系统倾向于混乱的趋势之间的博弈,达到一个互相都满意的状态。系统的熵固然必须尽可能大,但是此处综合了自旋反平行趋势的影响。
几种力量的博弈
在温度不太高的情况下,自旋之间的反平行趋势占优,最终会呈现为规则的排列。反之,如果温度足够高,熵增的趋势占据主导地位,则这种秩序性将被破坏。这是一个秩序与非秩序的博弈过程,实际上是看秩序性降低的能量使自由能降低得更多,还是非秩序性提升的熵使得自由能降低得更多,谁使自由能降低得多,谁的效果就占据主导地位。
这时,如果加上一个让全部自旋平行排列的趋势的外磁场,就会变成三种力量间的博弈:如果外磁场特别强,它将战胜另外两股力量,最终形成自旋平行排列的阵列结构;如果温度特别高,而磁场力量不够,最终的状态应该是混乱的;如果温度不够高,而磁场也不够强,阵列会形成反平行排列的结构。
除了平行、反平行、混乱三种比较明显的状态之外,随着温度、磁场、自旋相互作用强度几个参数的不同变化,阵列还有可能形成多种不同的形态,这些不同的形态就是伊辛模型不同的相。当这些排列的物理性质以及解决难度发生改变,我们就说这个系统发生了相变。
通过调节不同参数,能解出在不同参数条件下,系统会呈现出什么样的相。可调节的参数非常多,除了温度、磁场、相互作用的强度以外,我们还可以改变系统的维度,一维、二维、三维的阵列形态的物理性质以及解决难度是完全不同的。
除此之外,还可以把阵列中的电子排布成不同的几何形状,比如排成三角形。这种形态的阵列解起来尤其复杂,对于一个三角形单元来说,无法做到正方形阵列那样的反平行排列,总会有一个非常尴尬不知道应该上还是下的自旋。
一般研究伊辛模型会假设只有相邻的自旋之间有相互作用,可以拓展一下,让相互作用并非只在相邻的电子间发生,还可以隔一个电子发生,这样的行为就更加有趣了。也就是说,对应于现实中不同的材料,我们可以做各种各样的参数调整,如此一来,解各种形态的伊辛模型将会是我们研究固体相变的一种重要手段。
对铁磁体性质的研究,只是伊辛模型的一项功能。伊辛模型虽说是个老问题,但是在参数变化的情况下,却没那么容易解决。近百年来,物理学家、数学家们尝试了各种办法,至今仍未彻底解决,而越来越多新的神奇形态从这个模型当中涌现,对于这个模型的研究,已经诞生了好几个诺贝尔奖了。
第四节 固体的光学性质
材料的光学性质,从宏观上大致分为透明与非透明,仅仅进行这样的粗线条描述是不够的,我们还要深入地分析,光是如何与材料的微观结构相互作用的。
既然来到了微观,我们就要基于光是电磁波的观点,通过研究电磁波与材料微观结构的相互作用规律,来描述材料的光学性质。
光如何与固体相互作用?
从宏观上看,光照射到固体上,总的来说有三种效果:反射、吸收和穿透。
反射很好理解,任何不是理想黑体的物体,都对光有反射作用,只有理想黑体会百分百地吸收光,用以升高内部原子中的电子的能量。由于高能量不稳定,它还会释放出电磁波,这部分电磁波就是热辐射。
但是,理想黑体在现实世界中并不存在,所有物体都会对光有一定反射作用。不同物体在光照射下呈现出不同的色彩,本质上是因为不同物体对不同频率的光的吸收程度不同,树叶是绿色的是因为它对绿色的反射率最强,对其他频率的太阳光吸收的比例高。
光被吸收的部分被用来提升原子内电子的能量,透射的部分则是穿透了材料。当然,穿透的形式多种多样,有不改变光的运动方向的,也有散射的。比如,天空之所以是蓝色的,本质上是因为蓝光的波长易于被大气里的分子散射,散射得各个方向都有,所以我们看到的天空呈现为蓝色。这种散射被称为瑞利散射(Rayleighscattering)。
金属为什么不透明?
被反射部分的物理学机制比较简单,我们比较关注的是光进入材料之后,如何与材料发生反应。
我们知道金属是不透明的,这是为什么?
我们把光当成电磁波来研究光进入材料后的行为。电磁波是变化的电磁场,既然是电磁场,就会和电荷发生相互作用。我们之前定义了,自由电子就是只要有电场作用在上面就能形成定向电流的电子。从能带的角度来看,要让电子的能量增加是没有门槛的。
绝缘体中的电子在加了电场后,要提升能量必须跨越一个有限大小的能隙,导致加电场并不一定能使其电子形成定向流动。
但是金属不同,只要有电场,它就能提升能量。电磁波既然是电磁场,碰到金属里的自由电子,它就注定会被电子吸收,使电子的能量升高。也就是说,电磁波是可以激发自由电子的。如此一来,电磁波就被自由电子吸收了,它们无法穿透金属,所以,金属是不透明的。
但是这也与电磁波的能量有关,可见光的能量都不高,所以会被金属内部的自由电子尽数吸收,但是能量高的X射线、γ射线,是可以部分穿透金属的。
透明的机制(mechanism of transparency)
金属之所以不透明,是因为自由电子易于吸收电磁波能量。那我们依此可以推测:透明的材料大多是绝缘的。这是因为透明材料必然没有大量的自由电子,否则电磁波进入之后很容易被吸收,不会呈现透明的形态。
透明的材料主要是绝缘体,是因为原子中的电子都被原子束缚住了,并不自由,或者说它们的能带处于填满状态,能隙还很大,电磁波没有办法把电子激发到更高的能量状态。
但是,电磁波并非畅通无阻地通过透明介质,它还会与电子有相互作用。这种相互作用不是永远地把电子激发到高能形态,而是使电子在电磁波的作用下振动。由于高能不稳定,它会原封不动地按照原来的电磁波频率释放出新的电磁波,新释放的电磁波与入射的电磁波综合在一起形成了新的光。
电子与电磁波相互作用,放出频率相同的电磁波的现象,与之前提到的激光的受激辐射的过程类似。
折射率(refraction index)的机制
透明物体与电磁波的作用过程,解释了什么是折射率。
我们知道光有折射现象,光从一种介质射入另外一种介质,如果这束光不是垂直于两种介质交界处的平面射入,它的路线会转过一个角度,这就是光的折射现象,可以用光在两种介质中的折射率不同来解释。
光在真空中的速度除以光在介质中的速度就是折射率。这种光在介质中减速的效果与光和受原子束缚的电子之间的作用有关,也就是说,从电磁波被电子吸收再到电子放出一个频率相同的光子,这个过程需要时间。从总体的效果来看,就是电磁波传播的速度减慢了,等效体现为存在折射率。
实际上,折射率不单单是一个数值。透射出来的光,是入射的电磁波与被电子吸收再放出的电磁波的叠加,也就是说,最后射出的光是一种总效果。电磁波满足叠加原理,入射的波和电子受激发后再放出的电磁波有干涉现象,根据电子吸收再放出的电磁波的情况的不同,最后射出的电磁波也有不同的性质。电子射出的电磁波,大概率与入射电磁波的相位不同。
如果入射波和射出波刚好差1/4个波长,这种叠加总体上会使得光减速,呈现为普通透明介质折射率的效果;如果差的是1/2个波长,就会干涉相消,这样透明性就没有了,这种绝缘材料就不透明了;如果是刚好差波长的整数倍,这种材料很少见,它的性质跟激光的形成过程很像。
随着电子放出电磁波与入射电磁波的关系的不同,材料表现出不同的光学性质。
光子晶体(photonic crystal)
解电子在晶体中的能带结构时,我们了解了周期性的薛定谔方程,也就是说,薛定谔方程解出来的能带和能隙的结构,其实只是用了布洛赫定理,周期性的波函数无非是一列做了局部修正的正弦波。
描述量子力学规律的方程式是薛定谔方程,它只是波函数的一个波动方程。电磁波是波,它满足麦克斯韦方程,也是个波动方程。既然都是波动方程,就可以借鉴能带结构的规律发明一种材料,它能像电子的能带结构一样让电磁波在材料里传播时拥有能带结构。
也就是说,这种材料对光的频率有选择性,有些频率的光可以通过,而有些频率处在能隙范围里的光则无法通过。这种材料就是光子晶体,它的原理是让不同折射率的材料呈周期性排布,这样一来,我们在写电磁波在晶体里的波动方程时,会发现它的形式和算布洛赫波时几乎是一致的,我们可以类似地解出能带结构。对于光子晶体的研究,是非常前沿的研究方向。
至此,我们完成了固体物理这一章的讲解,但是固体物理是博大精深的,此处只讨论了固体物理的一些基本方法论。
固体物理研究材料的性质千变万化,而且研究深入之后,它的应用价值非常高。从材料学过渡到固体物理,可以说是研究的尺度越来越小,越来越细,从经典理论过渡到了量子理论。
目前说到的固体性质,是在室温环境下的固体的性质。虽然跟“极热篇”的温度比起来也算“极冷”了,但是室温的温度离“极冷”还有很远的距离。真正的极冷是当我们把温度降到接近绝对零度,几乎排除热运动的影响,这样多粒子系统的量子性质才会彻底显现。就像在讲铁磁体时说的温度足够低,铁磁体这种神奇的物质形态就展现了出来,这恰恰是一种多粒子系统的量子属性。
