凝聚态物理
第一节 玻色-爱因斯坦凝聚
凝聚态物理,顾名思义就是研究处在凝聚物态的物理系统的性质。这里的凝聚物态,跟“极热篇”讲的系综一样,研究的都是粒子数极其庞大的物理系统。区别在于,低温下物质的形态大多是液体和固体,液体、固体与气体不同,液体和固体分子之间有显著的相互作用,气体的分子之间则没有太强的相互作用,气体粒子是近乎自由的。固体和液体的分子和原子之间通过比较强的相互作用关联在一起,构成一种凝聚的状态,叫作凝聚态。
固体物理,也可以被认为是凝聚态物理中的一个部分,或者说是凝聚态物理的奠基性理论。只不过固体物理研究的固体形态较为规则,例如微观上呈几何规则排列的晶体,凝聚态物理的范围则更加宽泛。
现代的凝聚态物理,对于那些温度极低的物理系统非常感兴趣。在温度极低、粒子数量极大的情况下,凝聚态物理系统将变得很复杂,需要同时满足量子力学、电磁学以及统计力学的规律,它是一个综合性的物理学领域,会出现非常多神奇的物质形态。
量子力学与统计力学的博弈
在研究铁磁体时,我们就发现温度是影响固体形态的重要因素,不同温度会导致完全不同的固体形态,比如铁磁体的温度升高到超过居里温度,铁磁性就会消失。更专业的说法是,不同温度会导致物质处在不同的“相”。
在能带理论中,我们已经着眼于固体的量子性质了。做一个简单的推测,如果温度降到接近绝对零度,我们要研究的更应该是物质的量子性质。从微观定义出发,温度就是微观粒子原子、分子在做无规则运动。如果温度降低至接近绝对零度,原子、分子的无规则运动会减弱,这种情况下,基本粒子的量子性质会显得非常强烈。这其实是两种不确定性的博弈,当温度高的时候,原子、分子无规则运动的不确定性,会占据主导,量子的不确定性与热运动的不确定性相比之下没那么明显。这时候,我们关注微观粒子热运动的不确定性,这种不确定性可以用微观粒子的经典运动来表达,用统计力学的理论进行研究即可。
但是,温度较低时,量子不确定性原理的效果占据主导地位。量子层面的不确定性就不能用经典运动来表达了,统计力学也不够用了。根据量子力学的不确定性原理,微观粒子的位置和速度无法同时确定,只能用概率波来描述。
玻色-爱因斯坦凝聚
量子系统的一大特点,就是它稳定态的能量通常是量子化的。原子里电子能级之间有能隙,基态(groundstate)、激发态(excitedstate)的能量之间有能隙。电子是费米子,在原子中,电子按照能量由低到高一层层排布。但如果一个系统里的粒子都是玻色子,那么当我们给这个系统降温,会出现什么情况呢?随着温度不断降低,这些玻色子会往能量低的状态跑,可能会出现物质的第五形态——玻色-爱因斯坦凝聚的状态,这是爱因斯坦和一位印度物理学家玻色的共同研究成果。
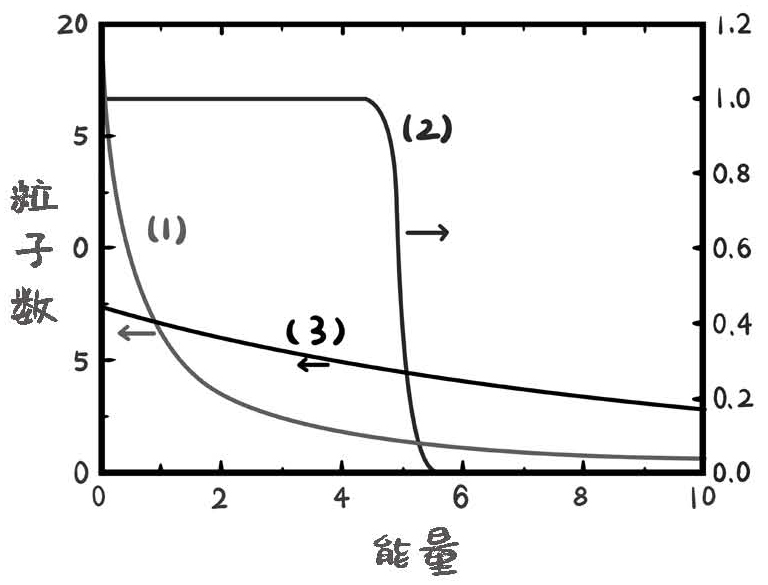
图20-1 低温时不同种类粒子能量的分布形态:(1)线,低温时玻色子能量分布,明显能量趋向于0时,处于基态的粒子密度趋向于无穷大;(2)线,低温时费米子的能量分布;(3)线,低温时常规的经典玻尔兹曼分布
玻色-爱因斯坦凝聚的机制不太好解释,但是我们可以来看一类特殊情况,这类特殊的玻色-爱因斯坦凝聚的状态,就是当温度低到一定程度,粒子的平均动能不比基态能量和激发态能量之间的能量差更大(大部分的玻色-爱因斯坦凝聚态并没有基态和激发态之间的能隙,我们只是讨论这种特殊情况来帮助理解),也就是大部分粒子无法因为热能被激发到能量较高的状态,这时大部分粒子会主动掉到能量最低的状态,这就形成了玻色-爱因斯坦凝聚状态,它是一个典型的量子化状态。只有玻色子能发生玻色-爱因斯坦凝聚,因为费米子要满足泡利不相容原理,不可能出现众多费米子都同时处在基态的状态。
一个热力学系统内部粒子的速度分布应该是一种正态分布,这种正态分布体现为一条两头小中间大的曲线,也就是大部分粒子的能量应该出现在平均温度对应的能量附近。但是对于玻色-爱因斯坦凝聚的状态,由于能量的量子化特点在低温的时候变得非常明显,所以大部分粒子其实无法被激发到高能量的状态,所以大部分粒子就掉到了能量最低的状态。这种情况下,玻色-爱因斯坦凝聚系统中粒子的能量分布就不是正态分布了。
这就是温度降低,量子力学占据主导,不再满足经典统计力学的一个最好的例证。
超流体
除了玻色-爱因斯坦凝聚这种神奇的物质形态以外,还有一种特殊的物质形态,叫作超流体。超流体通常都处在玻色-爱因斯坦凝聚的状态。
超流体,可以简单理解为内部摩擦力为零的流体,在20世纪上半叶就已经被发现。当氦气被降温到4K(相当于-269℃)左右时,形成的液氦流体是一种超流体。与我们平常认知的普通流体完全不同,如果让超流体开始流动,它永远都不会停下。搅动一桶水,它最终肯定因为内部摩擦力而停下,但是轻微搅动一桶超流体,它永远不会停下来。
超流的状态,跟玻色-爱因斯坦凝聚有很大关系,超流态往往是玻色-爱因斯坦凝聚的状态。超流的微观机制,到今天都没有完全弄清楚,但是如果单从现象出发,我们可以通过分析玻色-爱因斯坦凝聚,给出一定的解释。
我们上一章提到过,一个满足统计规律的系统的稳定态一定是对应自由能最低、熵最高的状态,也就是说,它要自发降低自己的自由能。一桶水这样的普通流体的摩擦,本质是因为可以通过摩擦降低自由能,摩擦生热,热提升熵,熵的提升会降低自由能。如果超流体没有摩擦,从自由能的观点看,就是超流体无法通过丧失动能来减小自由能。
普通液体的内部摩擦本质上是流动的液体要把运动的动能,给到周围的其他的动能没那么高的流体。超流体既然不会降低流速,换个角度看就是超流体的动能“给”不出去。
流体如果已经处在玻色-爱因斯坦凝聚的状态,则大部分的粒子处在能量最低的基态,这时由于量子力学的性质占据主导,基态跟激发态的能量之间有一个能隙(此处为方便理解,我们讨论存在能隙的情况,广义的超流机制则更加复杂)。要把这些处在基态的粒子能量升高到激发态,至少要给到多于基态和激发态能隙之间的能量。
超流体的流速都不高,只能较为缓慢地流动。因为有能隙存在,超流体中流动的粒子的动能也不是很高,这个动能如果不超过基态和激发态之间的能隙,就无法把这些能量给出去。这就好像你在某个停车场停了一晚上车,第二天准备出去的时候,停车费要100元,但是你身上只带了50元,不够付,显然你就出不去了,这里的道理是类似的。
当运动粒子的能量给不出去,无法让周围基态粒子的能量升高的时候,它就只能一直保持继续流动的状态,体现为一种超流的形态。
从超流的现象,我们可以初步看到,量子力学在低温世界开始充分展现它的效果。虽然说量子力学规律是低温物理系统里最重要的物理学规律,但本质上我们讨论的是多粒子系统的量子物理规律,这与研究单个粒子、原子性质时用到的量子力学技巧截然不同。
第二节 声子(phonon)
有了对超流体的认知,一个直接的联想,就是超导体,让超流体带上电,这不就是超导体了吗?但在讨论超导体之前,我们先要了解一个重要的物理学概念——声子,顾名思义,这是一种“声音”形态的粒子,它跟材料的声学性质息息相关。
为什么我们要在一个看似用量子力学讨论问题的章节讨论声学性质呢?声学跟量子力学似乎毫无关系,声波无非是机械振动而已。当然,低频的,人耳可听到的声波,甚至几万、几十万赫兹的超高频的超声波,都不会涉及量子力学。声子可以被认为是声波的量子化,就好像光波的量子化叫光子一样,声波的量子化就是声子。
晶格振动(latticevibration)
声音到底是什么呢?从物理学的角度来看,声音就是一种机械振动。比如,声音在空气里传播,空气分子在声波带动下传递这种振动,形成了声波。声波也可以在固体中传播,由于固体拥有更大的密度,分子之间的距离更近,相互作用更加迅速,所以固体中的声速要高于空气中的声速。
在讨论晶体能带结构的时候,我们做了一定的模型简化,假设晶格(crystal lattice,晶格指的是晶体结构当中原子平衡位置所处的几何位点)上的原子核不动,只是提供正电荷,让电子感受到多个正电荷的电势能。但实际情况并非如此,晶格的振动是存在的。固体之所以能形成,是因为原子之间有相互作用力(不论是范德瓦耳斯力,还是形成了化学键),这个相互作用允许原子在平衡位置附近振动,否则就成为刚体(rigid body)了,而我们知道刚体只是物理学的理想模型,现实中并不存在。当然,固体里的原子只能在平衡位置周围振动,如果能自由移动就不是固体,而是液体或气体了。
晶格振动的量子化
原子的振动从根本上也遵循量子力学的规律,可以用量子力学解原子按晶格排列的薛定谔方程。它依然是一个按晶体的几何结构进行周期性变化的薛定谔方程,这样,我们就可以解出原子振动的能带结构。带和带之间存在能隙,能隙中间的这段频率无法在晶体中传播。
晶格的振动,亦即原子在其平衡位置周围的振动,应当被视为一种量子化的行为。宏观的机械波,其能量由机械波的振幅和频率共同决定。满足薛定谔方程的晶格振动能量则由它的频率唯一确定,也就是用薛定谔方程解出来晶格振动的行为不像波,而像粒子。晶格振动起来,把这种振动模式传递出去,振动模式在晶格之间传递,它就更像是粒子的行为,而非波的行为,因此这种量子化的晶格振动行为被称为声子。
我们不能通过增大某一种频率的声子振幅,来让它的能量更高,因为振幅是固定的、是量子化的,我们能做的,是增加这种频率的声子的个数。这就特别像在“极小篇”第十一章中讨论量子力学的最初问题——黑体辐射时所说,普朗克解释黑体辐射的基本假设就是光子的能量是一份一份的,声子的能量也是一份一份的。
声子到声波的过渡
经典意义上的声波(也就是机械波),有振幅,有频率,确实可以在固体里传播,这与声子的定义似乎是有冲突的。我们应该如何理解量子化的声子到经典意义上的声波的过渡呢?
普通的声波、人耳可以听到的,频率其实非常低,钢琴的音,频率大概也就是几百到几千赫兹,但是量子化的声子的频率是极高的,大约能高到1012赫兹,也就是一万亿赫兹的数量级。频率低,波长长(频率高,波长短)。
经典的声波波长都很长,普通声波的波长在厘米、分米,甚至米这样的数量级,当这种量级的声波进入固体,固体中的原子会随之做整体运动,任何两个相邻原子发生的位移几乎没有什么差别。
普通声波的传播是一种宏观行为,不涉及原子微观的运动,但是对于量子化的声子这样高频率、波长在纳米数量级的声波,相邻原子的运动方式会有巨大的区别。声波波长的长短,直接决定了应当考虑经典的宏观性质还是量子的微观性质。
第三节 超导(superconductivity)
超导现象就是物体的电阻为零,超导体就是电阻为零的导体。超导这种现象在20世纪初就已经被发现了。当时有一位荷兰物理学家,把水银的温度降到十分接近绝对零度时,发现这时水银居然超导了。超导的形成机制也多种多样,我们到今天也无法完全解释清楚。
BCS理论
电阻的本质是电子运输过程中的各种阻碍,比如与晶格的碰撞,这其实体现为一种摩擦。既然超流摩擦力为零,只要让超流体带上电,岂不就是超导了?但这里有一个巨大的鸿沟,超流通常都处在玻色-爱因斯坦凝聚状态,但是玻色-爱因斯坦凝聚只能发生在玻色子身上,而电子是费米子,费米子无法发生玻色-爱因斯坦凝聚,因此单纯给大量电子降温是无法达到超导的状态的。
最早关于超导的微观理论叫BCS理论,由三位美国物理学家约翰·巴丁(John Bardeen)、利昂·库珀(Leon Cooper)和约翰·罗伯特·施里弗(John Robertschrieffer)共同提出,BCS就是他们三人名字首字母的连写。该理论让这三位物理学家获得了1972年的诺贝尔物理学奖。
BCS理论的关键在于如何让电子变成玻色子,这里就要说到上一节提到的声子。在“极小篇”讨论过,粒子物理中,力的本质就是有粒子的交换。BCS理论的关键,就是两个电子通过交换声子,产生了一个等效的吸引作用。在交换声子的过程中,两个电子以自旋相反的方式被束缚在一起形成了一个电子对,这个电子对叫作库珀对(Cooper pair),它是一个玻色子。
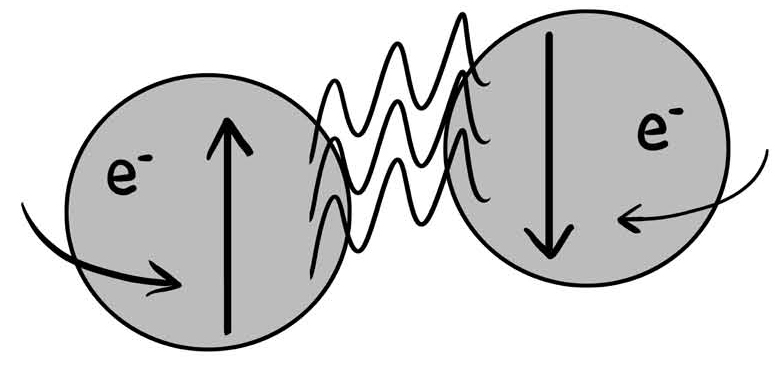
图20-2 库珀对
既然变成了玻色子,就可以发生玻色-爱因斯坦凝聚,成为超流,并且这个玻色子是带电的玻色子,因此就成了超导。
完全抗磁性
超导拥有完全抗磁性,也就是说,磁场无法进入超导体,它内部的磁场一定为零。
如何理解完全抗磁性?磁场进入超导之后,会激发起超导体里的电流,当然,并非只有超导体里会被磁场激发起电流,任何材质都可以。但是,由于超导体的电阻为零,电流一旦被激发起来之后就不会消失,电流会产生新的磁场,它与入射磁场的方向相反,会抵消入射磁场的强度,并且是完全抵消。如果不完全抵消,就会有新的电流被激发起来,新电流的磁场会抵消之前还没有被抵消的部分,因此最终的状态必然是所有磁场都被抵消(否则能量就不守恒了)。这样,超导体的内部才会是稳定的。这就是超导完全抗磁性的来源。
超导体完全抗磁性的分析和另外一种电学现象——静电屏蔽(staticshielding)现象的分析一样。为什么飞机即便被闪电击中,飞机内的乘客也不会受伤?为什么手机进入电梯经常没有信号?这些其实都是静电屏蔽现象。
静电屏蔽现象说的是,电场无法在金属中存在。如果金属中存在电场,那么这个电场会倾向于把正电荷沿着电场方向推动,把负电荷沿着相反的方向推动,正电荷和负电荷分开产生一个新的电场,这个新电场的方向与外部电场方向刚好相反,与外部电场相抵消,因此最终的效果是金属里的电场为零。之所以有这个现象,是因为金属里有大量自由电子,而绝缘体不行则是因为电场无法让绝缘体里的正负电荷充分分开。
所以金属拥有完全抗电性(静电屏蔽),超导拥有完全抗磁性。
高温超导
BCS理论对应的是最普通的一种超导体,这种超导的临界温度非常低,大概是液氦对应的4K。后来科学家们发现,超导的临界温度可以通过改变物质的种类进行提高,比如用结构十分复杂的化合物,能把这个温度提升到100K以上。
科学家们竞相提升超导的临界温度,这个研究领域变成了一个全新的领域,叫作高温超导。此处的高温并不是我们认为的那种几千、几万摄氏度的高温,而是跟绝对零度相比之下的高温,100K(-170℃)的临界温度,跟4K的液氦超导相比温度要高得多。
科学家们对高温超导原理的研究,目前也只是在半摸索的状态中前进,至今还没有完全弄清楚。主流的高温超导原理有若干种,但是万变不离其宗,大多需要形成库珀对,要想让电子形成库珀对,其机制,在高温超导中未必是通过声子,而是通过一些其他的方式。
有一种机制叫自旋密度波(spin density wave),可以这么理解,我们上一章通过伊辛模型讨论过铁磁体,也就是加了一个磁场以后,电子的自旋都倾向于平行排列。当然,我们也讨论了反铁磁体,也就是相邻的自旋倾向反平行排列。
自旋密度波说的是在低温情况下,这些电子的自旋情况与反铁磁体类似,它自身产生的磁场,倾向于让周围的电子都以反向平行的形态靠拢并形成反平行排列的电子对,如同波动在传播一样,因此叫自旋密度波。
超导的应用
超导的应用十分广泛,在“极小篇”里,粒子物理实验用的对撞机需要产生巨大的磁场来束缚粒子的运动,就要靠巨大的电流,但是一般的线圈在有电阻的情况下是无法支撑超大的电流的(因为发热量巨大),而超导在承受大电流方面就有天然优势。除此之外,为了束缚住一亿摄氏度高温的反应物,可控核聚变也需要用强大的磁场,这种磁场也是依靠超导来承载的。
如果高温超导(尤其是室温超导)能实现,将为人类的用电方式带来革命性的改变。我们目前之所以用的是交流电,是因为交流电可以通过超高的电压,降低在传输过程中的线路损耗。如果超导输电实现,超高压的交流电也许将退出历史舞台。
超导和超流可以说是在低温状态下最早被发现的奇异物理现象,从20世纪80年代起,低温状态下的奇异物理学现象越来越多,这开启了一个全新的物理学领域——强关联系统。
第四节 霍尔效应(Hall effect)
什么是霍尔效应?
超流和超导是凝聚态中比较奇特的物质形态,但凝聚态系统中的神奇物态远不止于此,20世纪70年代被发现的量子霍尔效应翻开了凝聚态物理中研究的新篇章。
什么是量子霍尔效应?
首先要了解一下普通的霍尔效应。霍尔效应在1879年由美国物理学家霍尔(Edwin Hall)发现。最初的霍尔效应其实很简单,将一块方形金属板两端接上导线通上电,导线里会有电流通过,这个时候垂直于金属板加上一个磁场,稳定之后就会在金属板垂直于电流方向产生一个电压。外加磁场并产生垂直于电流方向的电压的效应,就是霍尔效应。
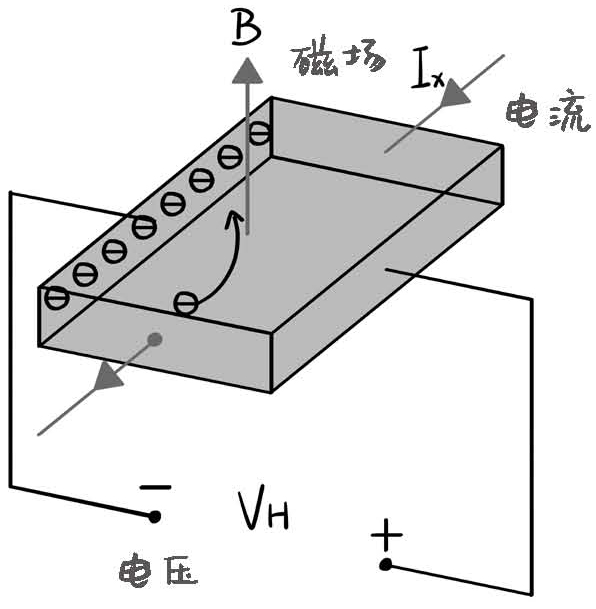
图20-3 霍尔效应的设置
为什么会产生垂直于电流方向的电压呢?我们知道,电流就是带电粒子的定向流动。由于有垂直于速度方向的磁场,带电粒子会在洛伦兹力的作用下拐弯,电荷打到金属板的侧面上并堆积起来。
堆积起来的电荷会产生一个电场,这个电场又会对电流里的电子产生库仑力,库仑力的方向跟洛伦兹力的方向相反。也就是说,当堆积的电子多到一定程度,库仑力和洛伦兹力互相抵消时,电荷堆积的现象就会停止。这时带电粒子的受力恢复平衡,它会继续往原本的电流方向运动。堆积的电荷会在垂直于电流流动方向产生一个电压,这就是霍尔效应。此处我们可以定义一个数值,叫霍尔电阻,它等于横向的霍尔电压的大小,除以纵向流动电流的大小。
霍尔效应的物理图像
霍尔效应要解释起来其实比较容易,但是神奇的是,20世纪70年代,科学家们发现了一种奇特的霍尔效应——量子霍尔效应。
在温度极低的环境下,把霍尔效应中的外磁场加强到一个极强的等级,就会出现量子霍尔效应,这时系统的霍尔电阻是一个量子化的数值。
普通的霍尔效应在加了一个磁场以后会达到稳定态,这时由于电荷的堆积会产生一个垂直于电流方向的电压,我们管这个电压叫V,原本的系统通电后会产生一个正常的电流,用字母I表示。我们定义一个数值叫霍尔电阻R,R=V/I。
霍尔电阻R应该跟什么参数有关?电阻等于横向电压除以电流,影响电流大小的有电荷密度,以及单个电荷的带电量,这里带电粒子就是电子,所以单个电荷带电量就是e。
堆积的电荷建立的横向电场产生的库伦力要跟洛伦兹力平衡,但是洛伦兹力又正比于外加磁场,由此可以简单推断,这个横向的电场应该与磁场的大小有关。可以想象,当我们调节外磁场的大小时,整个霍尔电阻也会随之变化,且变化图像应该是一条斜向上的平滑直线。磁场越强,堆积的电荷越多,相应的横向电压就越大,霍尔电阻就应该越大。
如果我们把磁场加到很强,强到10个特斯拉(Tesla,磁感应强度单位,地球的磁场只有1/100 Tesla左右,10T基本上是地球上能造出来的最强磁场的等级了),再将温度降低到1K左右。这个实验的效果非常神奇,我们会发现这个霍尔电阻随磁场大小而变化的图像,画出来居然是一个阶梯状。
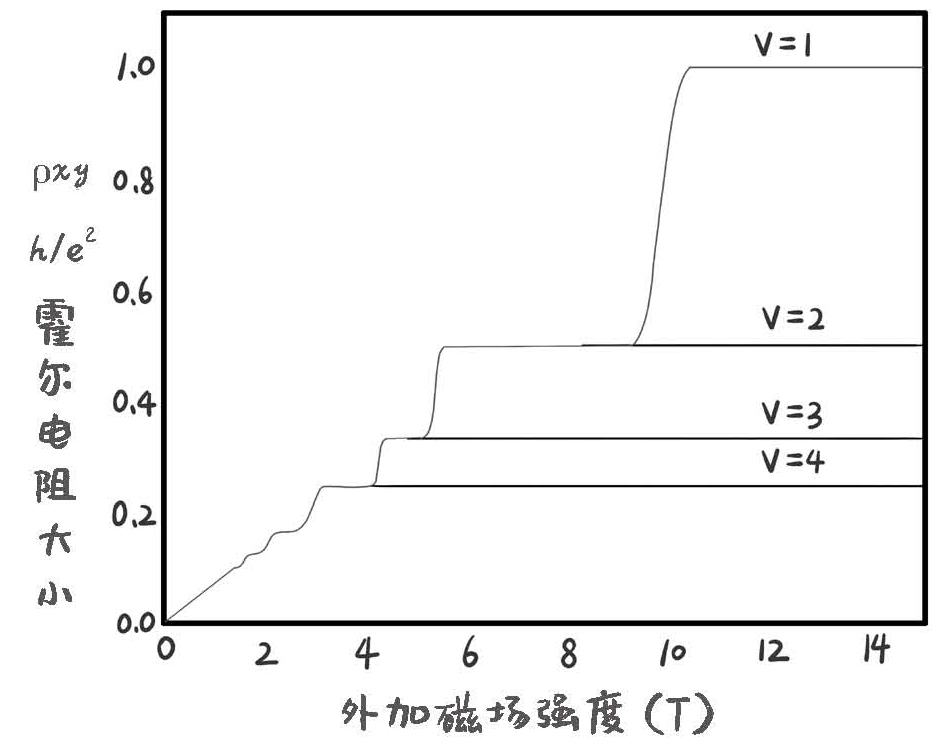
图20-4 不同磁场强度下的霍尔电阻
也就是说,随着外加磁场的变化,当磁场很强的时候,霍尔电阻在一定范围内都是一个精确的恒定值,只有当磁场再上一个大台阶,电阻才会有一个大的跳跃,然后再到一个新的恒定值稳定住。这每一个台阶的霍尔电阻的大小,其实可以写成(1/ν) h/e2,ν是任何正整数,可以是1,2,3,4……也就是说,霍尔电阻的大小其实是以整数分之一个霍尔电阻单位来变化的。ν叫作填充因子(filling factor),它的具体物理意义稍后介绍。
并且这个电阻的阶梯形特别稳定,哪怕金属板形状有变化、纯度不高,一些细微的扰动和变化都不会影响霍尔电阻的阶梯形,它的数值是一个精度达到了1/1010的精确度的整数,也就是误差不超过百亿分之一的精确度。
明明外加磁场是连续变化的,为什么霍尔电阻却按整数规律、离散地变化呢?其实说到离散,就想到量子化,并且这个电阻里还有普朗克常数h,说明与量子力学有关。极低温下,正是多粒子系统量子力学效果占据优势的时候。
接下来我们继续来讨论,如何理解量子霍尔效应中阶梯化的霍尔电阻。
第五节 量子霍尔效应
量子化的霍尔电阻
如何用量子力学来分析量子霍尔效应呢?首先来想象一下当磁场比较弱的时候电子的运动轨迹。
磁场比较弱的时候,洛伦兹力小,电子在洛伦兹力作用下做圆周运动的半径比较大,因为力很小,没法让它产生很大的偏转。这种情况下,大部分电子起初都会被打到金属板的侧面。但如果磁场极强,这些电子会受到极强的洛伦兹力,甚至可以让这些电子原地转圈,形成一个个圆圈状的运动轨迹。
在这种情况下,这个金属板要想导电就没那么容易了。在金属板内部的电子都在原地转圈,就没有办法在电路里形成电流。但金属板边缘的这些电子还是可以形成电流的。金属板边缘的电子,我们假设它跟金属板边是弹性碰撞,正面碰上去之后会原速反弹继续形成一个新的半圆,转下去,再正碰,再反弹,如此反复。
所以,在磁场极强的情况下,只有边缘的电子可以参与导电。
有了这个认知,再来看看强磁场以及低温的情况下,金属板里电子的运动状态满足什么规律。我们显然不能再用经典的电磁学去描述这些电子的运动,而是应该用薛定谔方程去描述它们的量子行为。
之前在解原子内部电子的运动的波函数的时候,用到了薛定谔方程,它描述了电子的能量。电子的能量有两部分,一部分是电子的动能,一部分是电子受到原子核库仑力的电势能。
对于量子霍尔效应也一样,这个金属板里的电子有动能,并且由于金属里的电子是自由电子,所以外加磁场以后,电子的势能也只用考虑外磁场的势能,这样就可以求解金属板中自由电子的薛定谔方程了。那么很自然地,可以猜想这跟原子里的电子轨道一样,量子霍尔效应的薛定谔方程也可以解出能量的量子化。在量子霍尔效应里解出来的量子化的能级,叫作朗道能级,这是由苏联著名物理学家朗道率先发现的。
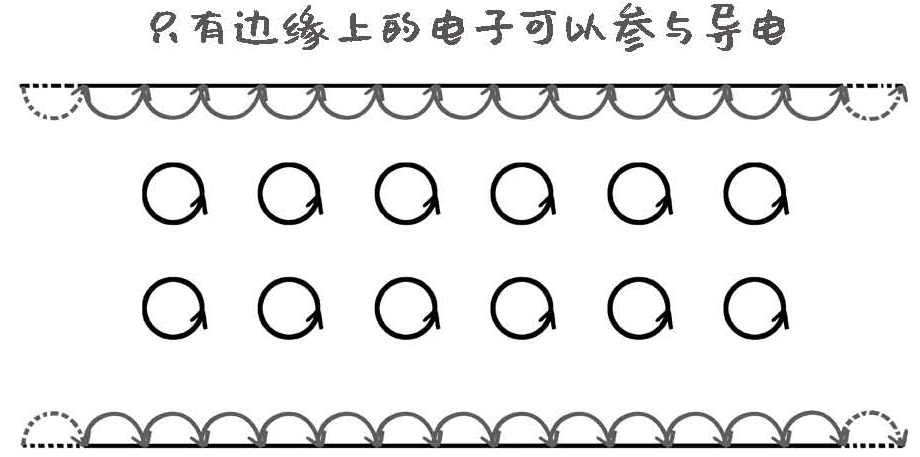
图20-5 金属板导电
每个朗道能级都可以放电子。在量子霍尔效应环境下的电子能量都是量子化的,至于具体处在哪个朗道能级,就跟在原子里把电子填到各个轨道里的过程一样,量子霍尔效应里的电子,要先填能量最低的等级,然后一个个往高能量等级填。
朗道能级怎么解释量子霍尔效应呢?霍尔电阻的阶梯状是怎么出来的?
这里要深入地理解一下霍尔电阻的定义,霍尔电阻就是横向电压比电流。根据图20-5,我们发现电流其实只跟边缘的电子运动状态有关。横向电压又跟什么有关呢?横向电压与堆积在金属板边缘的电荷数量有关,也就是跟堆积在金属板边缘的电荷密度有关。两个密度之比其实就决定了霍尔电阻的大小。
在变化磁场的情况下,如果金属板边缘的电荷密度与边缘电流的电子密度之比是一个恒定不变的值,这样就可以解释为什么霍尔电阻在提升磁场的情况下是一个恒定的值了。
通过解薛定谔方程可以发现,电子的不同能量等级对应了不同的朗道能级,也就是说电子在二维金属板当中,它的排布状态也是从低能量开始,填满了低能量的朗道能级,才会再填高能量的朗道能级。
来看单个朗道能级的特点。每个朗道能级中电子所处的运动形态,实际上是电子转圈或者转半圈的状态。电子转圈,本质是因为有磁场通过,电子围绕着磁场转圈,磁场强度越大转圈的半径就越小。因为磁场强度越大,洛伦兹力充当的向心力就越强,越强的向心力就能转越小的圈。每个圈代表了一个电子可以占据的状态。每个圆圈都有面积,磁场越强圆圈的面积就越小。定义一个物理量nφ,它是单位面积里能够存在的一个朗道能级所对应的电子转圈的个数。那么可以知道外磁场越强,朗道能级的圆圈的面积就越小,nφ的数值就越大。再有一个物理量,就是电荷密度,写成ne。前文说到的填充因子ν就等于ne/nφ。
我们现在来看一个朗道能级对应的圆圈所占据的面积当中,有多少电子,单个朗道能级所占面积中的电子数其实就是填充因子ν。我们论证,外磁场越大,ν就越大,则导电性越差,霍尔电阻就越大。当外部磁场增强的时候,单个朗道能级对应的圆圈面积就越小,单位面积中的朗道能级数量就越多,因此nφ就越小,根据填充因子ν的定义,ν越大。朗道能级的圆圈面积越小,这块面积当中存在的电子数就越少,因此在边缘上,能够参与导电的电子数就越少,参与导电的电子数越少就说明电流越小,电流越小则说明霍尔电阻越大。因此我们就论证了,即便在量子霍尔效应的情况下,增大外磁场也会使得霍尔电阻变大。
电阻的阶梯状又应该怎么解释呢?这里的关键是,正常情况下导体金属板不可能没有任何杂质,这种杂质体现为系统中的无序(disorder)效果,电子的运动状态是局域化地集中在紊乱地区附近的,它们都不参与导电,在外磁场强度变化比较小的过程中,这些局部的紊乱无法被破坏,因此在外磁场强度变化不大时,霍尔电阻呈现出稳定不变的特性。反而当系统极其纯净的时候,电阻的阶梯状是不存在的。
这就是为什么霍尔电阻在强磁场的情况下,不是连续变化,而是跳跃变化的。磁场的大小在一定范围内,霍尔电阻的变化呈阶梯状。
分数量子霍尔效应(fractional quantum Hall effect)
上述的量子霍尔效应是“整数量子霍尔效应”(integer quantum hall effect),整数量子霍尔效应当中电子之间的相互作用不计入在内,如果考虑电子之间的相互作用的话,就可以得到“分数量子霍尔效应”。华人科学家崔琦,就是因为在实验中做出了分数量子霍尔效应获得了1998年的诺贝尔物理学奖。
霍尔电阻不仅在强磁场下有整数变化的规律,还有分数变化的规律。分数量子霍尔效应可以说是打开了一个全新的领域,甚至可以说是把凝聚态物理的地位提升到了一个新的高度。分数量子霍尔效应意味着,我们可以通过凝聚态的量子系统去人为创造出一些自然界本不存在的物理学规律。
比如之前讲的基本粒子在量子统计规律上分为两大类:玻色子、费米子。如果两个玻色子相互交换位置,它们整体的波函数会获得一个数值是1的相位,比方本来的波函数假设是φ(x,y),x和y分别是两个玻色子的坐标,然后把两个玻色子交换,变成了φ(y,x),两个玻色子的交换会告诉我们,φ(x,y)=φ(y,x),但如果是费米子的话,它会获得一个-1的相位,也就是φ(x,y)=-φ(x,y)。
但是分数量子霍尔效应这个“分数”的意义在于,我们可以在量子系统中获得一些准粒子(quarsi-particle),它们并非粒子物理当中那些真实存在的基本粒子,而是凝聚态物理系统中被激发起来的一些量子行为,这些行为像是量子粒子的行为。其实我们前文提到的“声子”也可以被认为是一种准粒子,它不是粒子物理意义上的基本粒子,而是一个量子系统在某种情况下表现得像粒子(act like a particle),这些准粒子是从凝聚态物理系统中“涌现”(emergent)出来的。准粒子的概念最早也是由朗道提出的。分数量子霍尔效应中的一些准粒子在量子统计规律上,它们既不是玻色子也不是费米子。交换这两个准粒子,它们的波函数获得的相位不是1也不是-1,而是一个模是1的复数。这种统计规律叫分数统计(fractioanlstatistics)。当然,它们只能存在于分数量子霍尔效应这样的二维量子多体系统中。这些既不像玻色子也不像费米子的准粒子也被称为任意子(anyon)。
这样的任意子,目前在自然界看来是不存在的,也就是说,粒子物理的实验中完全没有发现这样拥有分数统计的粒子,粒子物理中也没有针对分数统计的理论。这完全是分数量子霍尔效应当中产生的奇特现象。这其实是给我们的基础物理研究指出了一个新方向,就是除了用高能对撞机不断撞出更小的粒子以外,我们还可以尝试用人为构造的凝聚态系统,模拟一些最基本的物理原理,分数量子霍尔效应就是一个很好的例子。我们通过这个凝聚态系统甚至模拟出了自然界中本不存在的粒子物理规律。这同时也启发了我们,准粒子是从凝聚态系统中涌现出来的,那么粒子物理意义上的这些基本粒子,是不是也是某些更加基本的“凝聚”当中“涌现”出来的呢?也就是,时空未必只有时间和空间,基本粒子并非独立存在于时空当中,基本粒子也许只是一些更基本的“凝聚”系统中的“涌现”。由华人物理学家文小刚提出的“弦网凝聚”(string-net condensation)阐述的正是这种思想,弦网凝聚理论中,电子和光子都是从弦网中涌现出来的。
第六节 强关联系统与量子计算
强关联系统(strongly correlatedsystem)
量子霍尔效应的发现,尤其是分数量子霍尔效应的发现,催生了一个全新的物理学领域——强关联系统。什么叫强关联系统?可以先回顾一下上一章讲能带结构的时候,对晶体当中电子、原子核进行的分析。
晶体里原子核带正电,电子带负电,其中有三组相互作用,分别是电子和原子核之间的电磁相互作用、原子核之间的电磁相互作用,以及电子和电子之间的电磁相互作用。通过分析,我们论证了一般晶体中原子核之间的相互作用是不显著的,因为在晶体里原子核的位置比较固定,即便有振动会产生声子,其贡献也无法达到质变的等级。晶体里电子和电子之间的距离也比较大,不会显著影响电子的行为,只有电子和原子核之间的作用是最显著的,我们在能带理论里只考虑了电子和原子核之间的相互作用。因此,才得出了能带理论来研究固体物理。
但是分数量子霍尔效应告诉我们:在很多情况(尤其是温度极低的情况)下,电子的量子特性占据主导,存在很多电子和电子之间的相互作用不能忽略的情况。这其实就是强关联系统在研究的问题。强关联中的强,指的就是系统中电子和电子之间的相互作用强到不能忽略了。前文的超导,考虑的就是电子和电子之间的相互作用,两个电子通过交换声子形成电子对,从而发生超流并形成超导。再譬如前文提到过的莫特绝缘体,像氧化镍(NiO)、氧化钴(CoO)和氧化锰(MnO)这样的化合物,若是按照能带理论进行分析,它们应当是导电性良好的导体,但是实际上它们却是透明的绝缘体,这当中的原因就是能带理论是不考虑电子间相互作用的,然后在莫特绝缘体当中,电子之间的相互作用已经强到不能忽略,因此能带理论不再适用。
上一节的分数量子霍尔效应,也是因为电子之间的相互作用非常明显而导致的。因此,强关联系统是一个非常值得研究的课题,它是凝聚态物理中最前沿的研究领域。
量子纠缠
此处可以回顾一下“极小篇”当中提到过的一个概念——量子纠缠。
量子纠缠是指几个量子系统同时处在一定的叠加态,比如两个电子,它们同时处在同为自旋向上和同为自旋向下的状态。这个时候探测其中一个电子的状态,就能立刻知道另外一个电子的状态,不用进行额外的探测。
强关联系统里的电子,是可以处在量子纠缠态的。我们在讲伊辛模型时提到过,一个二维的电子自旋阵列,它可以形成一个大的涡旋的阵列,这就是一种量子纠缠的状态。也就是说,这些材料里的电子之间虽然有相互作用,但其实是短程相互作用,每个电子主要还是受到离它近的电子的作用。
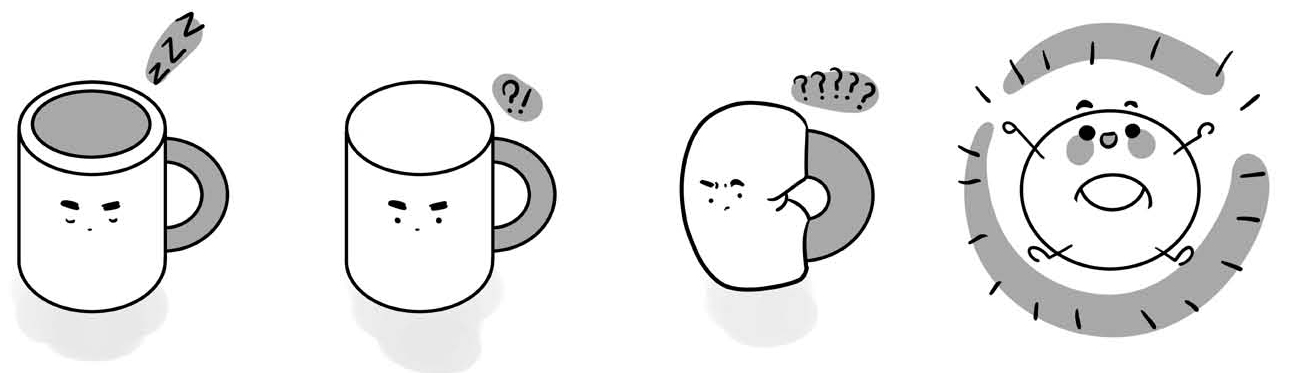
图20-6 咖啡杯的拓扑结构和甜甜圈是一样的
神奇的是,由于量子力学的效果,这些电子的形态有可能形成长程关联(long-range entanglement)的形态。
这些长程关联的形态涉及了几何学中一个重要的分支——拓扑学。拓扑学简单来说,就是不关心几何图形的具体形状,只关心它们的连接方式。比如,一个有把手的咖啡杯,在拓扑学上跟一个甜甜圈是一样的,在拓扑学看来它们是同一个东西,因为它们都只有一个洞。
如果用橡皮泥捏出一个咖啡杯,我们可以在不补上洞的情况下,再把它捏成一个甜甜圈。但是一个球就不行了,球体是没有洞的,你要把它捏成一个咖啡杯,是必须要在上面挖一个洞,或者要把它拉长两端粘在一起。
也就是说,我们无法顺滑地把一个物体变化成一个拓扑结构跟它不一样的物体。拓扑结构意味着稳定性,一个拓扑结构一旦形成,连续、顺滑的扰动和干扰无法改变它的拓扑结构。
当这些量子粒子形成长程关联以后,这种长程关联也会构成一个拓扑结构。这个拓扑结构非常稳定,我们无法顺滑地把它变成一个其他的拓扑结构。也就是说,一旦一个量子的长程关联形成了以后,只是给这个系统做一些轻微的扰动,其结构不会改变。
这就是为什么一旦磁场足够强,温度足够低,形成一个量子霍尔效应系统以后,霍尔电阻不会随着金属板形状、纯度的变化而变化,这就是一个神奇的拓扑性质。根据我们中学学的,一块材料的电阻是跟它的形状、横截面积、纯度息息相关的。但是一旦变成量子霍尔效应,这些形状、横截面积、纯度等都只是对于系统的轻微扰动,不会从根本上改变系统的性质。这样的材料就构成了一种拓扑材料,它对于量子计算机的研发有很大的帮助。
量子计算与拓扑材料
量子计算机为什么那么强大呢?因为它与电子计算机的计算原理有着本质上的不同。
我们知道,电子计算机用0和1的二进制信号来代表信息。一个电子只能代表0或者1,非此即彼,非常明确。但是量子系统就不一样了,一个量子状态的电子可以处在叠加态。例如我们可以用电子自旋向上的状态代表信号1,用电子自旋向下的状态代表信号0,一个电子的状态可以是1和0的叠加态。
假设有两个相互纠缠在一块儿的电子,它们可以同时表达四个状态,分别是00、01、10和11。如果是3个电子纠缠在一起,就能表达8个状态,也就是000、001、010、100、011、101、110和111。
依此类推,N个纠缠在一起的电子,就可以表示2N个状态。这2N个状态就对应了2N个不同信息的信号。前段时间谷歌号称实现的量子霸权(quantumsupremacy),就是53个纠缠在一起的量子比特。用53个量子比特,就可以表示253个信息,这是巨大的信息量。
根据计算的原理,量子计算机的计算能力对电子计算机的碾压是指数级的。这也是为什么量子计算机可以在几分钟内完成传统计算机要算一万多年的计算任务。但是量子计算机有一个实际操作上的巨大问题,它对于误差、微扰太过敏感。由于量子力学的不确定性,微扰、误差一旦发生,这个错误完全是随机的,这就导致即便想要人为修正也变得不可能。
拓扑材料就有希望解决这个问题,拓扑材料是极其稳定的,如果只是有一些微扰和误差,并不会影响拓扑材料的量子状态。因此可以想象,我们用拓扑材料做成的量子计算单元将对微扰免疫,十分稳定。因此,拓扑材料的研究对量子计算来说,有着非凡的意义。
这也是为什么在今天的物理学界,对于拓扑材料的研究,是最前沿、最热门的领域。
至此,“极冷篇”讲解完毕。总的来说,温度比较低的形态,大多处在固体的形态,因此我们先从宏观的角度分析固体的各种性质,有力学性质、热学性质、电学性质和磁性质等。
固体的性质说到底还是由它们的微观结构决定的,因此我们不得不深入地去从量子力学的角度来研究固体的微观性质,由此引出了固体物理这门学科。能带理论是固体物理中最重要的理论,但是固体物理远非我们对于固体研究的终点,因此需要进入低温物理领域进行研究。
任何固体都拥有温度,但是温度导致的粒子无规则运动和粒子的量子特性处在相互博弈的状态,当我们把系统温度降低到接近绝对零度的时候,微观粒子的量子特性会变得极其显著。微观粒子之间的相互作用,如电子之间的相互作用,都会极大地影响物质形态和物质的特性,这也是为什么凝聚态物理,尤其是其中的强关联系统、拓扑材料会变得如此热门,因为它的形态太丰富了。凝聚态系统启发我们,除了用直接的方法追究宇宙终极,还可以用凝聚态系统模拟的办法去制造我们从未见过的物理学系统,去发现我们从未在自然界中发现过,甚至原本并不存在的性质。
