广义相对论的基本原理
第一节 引力究竟是什么
万有引力的遗留问题
根据牛顿万有引力定律,天体之间存在相互吸引的引力,在引力的作用下,天体的运行遵循各种各样的椭圆轨迹。万有引力的大小正比于二者质量的乘积,反比于二者之间距离的平方。
牛顿定律极其简洁优美,它似乎很好地解释了宇宙中所有天体的运行规律,但是当中有以下两个看似不是问题的问题。首先,天体是如何感知到另外一个天体的引力的(它们之间并没有实际的接触),也就是说,引力是通过什么传递的?比如,地球围绕着太阳运动,是因为地球感受到了太阳的万有引力。但是很显然,地球和太阳之间是空的,太阳没有用一只手抓着地球让它旋转,而地球也不长眼睛,它也不知道哪个地方有个太阳,它怎么就知道应该绕着太阳旋转呢?
其次,一个天体感受到的另外一个天体的引力是不是瞬时(instantaneous)的?如果太阳突然消失,地球会瞬间知道太阳没了吗?地球受到的引力会突然消失吗?我们知道,甚至连光的传播都是需要时间的。我们现在看到几光年以外的天体发出的光,其实承载的是这个天体几年前的信息,它发出的光要花几年时间才能传到地球上。那么引力呢?引力的传递难道不需要时间吗?这个作用是瞬时的吗?用牛顿的话说,引力的作用是超距作用(action at a distance)吗?
图7-1 超距作用
超距作用,就是引力是否能超越距离的障碍,瞬间作用到对象上。关于这个问题,牛顿有过思考,但是他并没有得出结论。在牛顿的万有引力体系里面,我们默认引力的作用是超距的。
总结一下,这两个关于万有引力的问题是:(1)引力的传递是否需要介质?如果需要,这种介质是什么?目前看引力是在真空中可以传递的;(2)引力的传递是不是超距瞬时的?这两个问题其实都是牛顿万有引力定律不完备的地方,需要爱因斯坦的广义相对论来回答。
引力是力吗?
广义相对论对引力有一个惊人的认知,那就是引力不是力,爱因斯坦认为引力是物体在扭曲的时空中,运动状态背离匀速直线运动的效果。
先来回答上面第一个问题,天体之间的引力通过什么传递,譬如:地球是怎么感受到太阳的引力的?广义相对论的解释是,地球和太阳中间并不是真空的,它们中间有时间和空间。广义相对论把时空看成了一种媒介。这就好比一条深海的鱼,一辈子都生活在水里,水是它生活的背景。如果这条鱼一辈子都不到海面上透气的话,它根本意识不到水的存在,因为水对于它来说太自然了。
人类也是一样,我们的存在是建立在时空基础之上的,没有时空何来存在?而时空本身也是一种存在。
既然时空是一种存在,我们应该能对它进行操作,让它发生变化。那怎么让时空发生变化呢?爱因斯坦给出的答案是依靠质量,质量会扭曲周围的时空。
比方说有一张桌布,找几个人把这张桌布的四角撑开,然后在桌布上放一个铅球,铅球的重量会把桌布往下压。这个时候,如果在铅球边上放个乒乓球,那么因为桌布的凹陷,乒乓球会向铅球滚过去。宏观上看,乒乓球好像受到了铅球的引力一样。但实际上,引力并不存在,乒乓球只是感受到了桌布的扭曲而已。
质量的作用就像铅球一样,把它周围的空间都扭曲了。地球并不知道太阳的存在,它只是感受到了时空的扭曲,于是开始了运动。只是这个运动的效果,总体上看好像是它受到了力的作用一样。
牛顿为了要解释这个运动,才发明了万有引力的概念。而广义相对论下,万有引力并不存在,它只是描述天体运动的一种模型。
再看第二个问题,引力的传递是不是瞬时的?有了爱因斯坦时空扭曲的解释,这个问题也就好回答了:引力的传递当然是需要时间的,它不是超距作用。
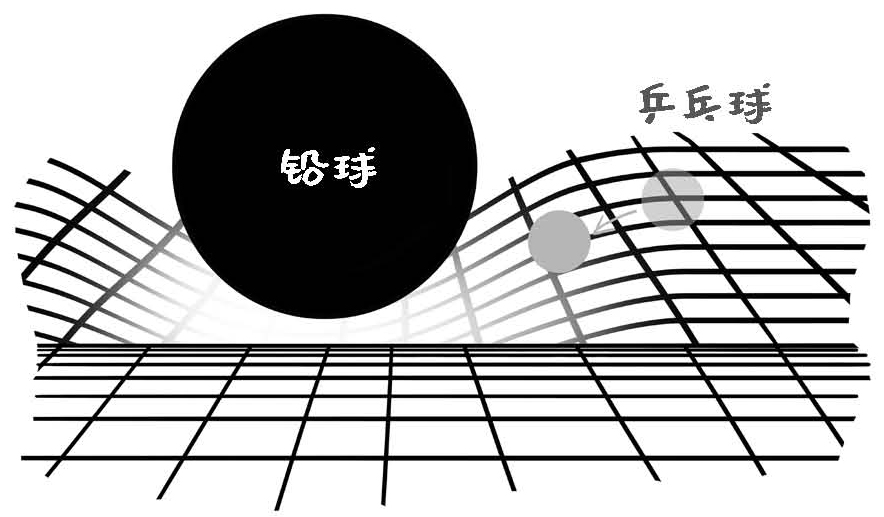
图7-2 现实中的时空扭曲类比

图7-3 引力波
这就好像往水里扔块石头,水会泛起涟漪,这个涟漪会以一定的速度向周围传播。引力也是如此。如果太阳突然消失了,地球感受到的时空扭曲不会突然消失,而是要经过一段时间才会消失。那么引力的传播速度是多少呢?答案恰恰就是光速,这是广义相对论的结论。
像水波一样,如果让空间中一个位置的质量忽大忽小,那么它周围的时空扭曲也会一直发生变化。这种变化会以光速传播出去,就产生了引力波。
运用广义相对论,牛顿万有引力当中两个悬而未决的问题就获得了解答。
时空的扭曲
在桌布的例子中,桌布是个二维平面,在铅球的作用下向三维扭曲。而我们的空间是三维的,要如何想象三维的扭曲呢?
我们可以把空间想象成一块海绵,海绵是可以被压缩的。空间的扭曲,其实就是因为质量的出现,让空间这块海绵的每个位置都经历了压缩。引力越强的地方,受到的压缩就越强。时空中每一块区域遭受的扭曲程度不同,那这些地方的物理属性就会发生变化。只不过时空这块海绵的扭曲,表现为时间变慢(钟慢效应)、空间缩短(尺缩效应),跟在狭义相对论中看到的效果是类似的。
第二节 等效原理(equivalence principle)
广义相对论“广”在哪儿?
狭义相对论的结论都是依据两条公理推导出来的,也就是狭义相对论原理和光速不变原理。那广义相对论的原理是什么呢?答案是等效原理。当然,在广义相对论当中光速不变原理依然成立,可以认为狭义相对论实际上是广义相对论的特殊情况,特殊到只讨论匀速直线运动、所有加速度都是零的情况。
和狭义相对论相比,广义相对论讨论的范围自然是更广泛的,广在哪儿呢?广到它考虑了加速的情况,并把引力也考虑在内。
引力和加速度是一回事
等效原理,总结起来一句话,那就是:引力和加速度其实是一回事。当然,等效原理有很多种表述方式,比较正式的表述方式是:引力质量(gravitationalmass)与惯性质量(inertialmass)相等。这些表述方式实际上是相互等价的,此处我们姑且关注引力与加速度等效的表述。
加速度的概念相对简单(见“极大篇”第六章),而等效原理传递了一个信息:只要理解了加速度,我们就理解了引力。
据说有这么一个小故事。当年,爱因斯坦和居里夫人,还有几个科学家一起去爬山,看到山上的缆车上上下下,于是爱因斯坦得到了一个启发:如果这个时候缆车的缆绳断了,缆车做自由落体运动,那么缆车里的人所感受到的状态应该和在太空中完全失重的状态是一样的。
顺着这个思路,我们来把这个问题分析得更全面一些。
假设普朗克在一艘宇宙飞船里,飞船没有窗户,看不见外面,隔音也很好,听不见引擎声。这个时候,如果宇宙飞船静止在太空中,或者以匀速直线运动的状态飞行(没有任何加速度),那么根据经验,飞船应该处于失重状态。
此时,如果普朗克手上有一个苹果,并把苹果放开,那么这个苹果不会落到飞船的地板上,而是飘浮在原来的位置。
再来考虑另外一种失重状态——自由落体运动。如果这艘宇宙飞船从高空下落,让它自由下落到地球上,普朗克再在飞船下落的过程中放开手中的苹果,对于他来说,苹果还是会飘浮在原来的位置,不会落到飞船的地板上。所以,普朗克完全无法区分宇宙飞船到底是在做匀速直线运动,还是在做自由落体运动,因为他和苹果都处于完全失重的状态。
用物理学的语言来说,在这两种情况下,普朗克做任何物理实验都无法判断自己的运动状态到底是处于静止、匀速直线运动还是在一个重力场中做自由落体运动。但是从飞船外的观察者看来,普朗克的运动状态是不一样的。
无论是在没有引力的太空中,还是在自由落体的过程中,你都感受不到任何力作用在你身上。这就隐约地告诉我们:引力不是力,只是一种加速效果。这就是等效原理想要传递的信息:一个加速参考系中的物理规律,和一个处在同等引力场里的参考系中的物理规律,是完全一样的。
自由落体运动
再举一个跟自由落体运动相反的例子:普朗克还是坐在一艘宇宙飞船中,飞船没有窗户,看不到外面,隔音很好,无法判断发动机是否在工作。
这个时候突然让宇宙飞船运动起来,以一定加速度开始加速向上运动。我们可以调节发动机,让飞船的加速度等于地球的重力加速度。这个时候,坐在宇宙飞船中的普朗克,会感觉自己突然有了重量。且因为飞船的加速度等于地球的重力加速度,他称一下自己的体重,会发现跟在地球表面称出来的体重是完全一样的。
用物理的语言来说,在一艘以地球重力加速度向上加速运动的宇宙飞船中,和在一艘放置在地球表面的宇宙飞船中,普朗克在船舱里做任何物理实验,都将得到一样的结果。
在加速的宇宙飞船里,普朗克手上拿个苹果放开,苹果会自动落到飞船的底部。对飞船里的他来说,就好像这个苹果经历了自由落体掉到了飞船底部一样。他完全无法区分自己到底是在一艘加速运动的飞船中,还是在地球表面。
我们站在地球表面或加速上升的宇宙飞船里,会觉得自己受到了重力的作用,这个力其实是地球表面给你的支持力,并不是来自引力。因此,引力的效果不是让我们感受到力,而只是让我们加速运动而已。根据这些思维实验,我们可以总结出一个推论:引力是加速效果,它不是一个真实的力。

图7-4 等效原理
第三节 什么是时空扭曲
从等效原理出发,如何能推导出“引力体现为时空是扭曲的”这一结论呢?
思维实验:光会拐弯?
首先,我们要用等效原理来证明光会在引力场的作用下走曲线。
还是来做一个思维实验,假设太空中有一架电梯,电梯不置身于任何引力场中。只要它不加速运动,站在电梯里的人就处于失重状态。
现在让电梯开始加速向上运动,这个时候,电梯里的人就有脚踏实地的感觉了,能够感受到自身的重量。不妨假设这个电梯是有窗户的,当电梯向上加速运动时,它的窗户经过一个激光器,激光器发射了一道光到电梯里。
对于电梯外的观察者来说,他看到的光的路径,应该是从左到右的一条直线,这道光也觉得自己走了一条直线。
而对于电梯里的人来说就不一样了。光速虽然很快,但还是有限的,光从左边射到右边需要一定的时间。在这段时间里,电梯已经向上加速运动了一段距离,因此,对于站在电梯里的人来说,看到这道光打到右边的高度一定是低于原来的高度。
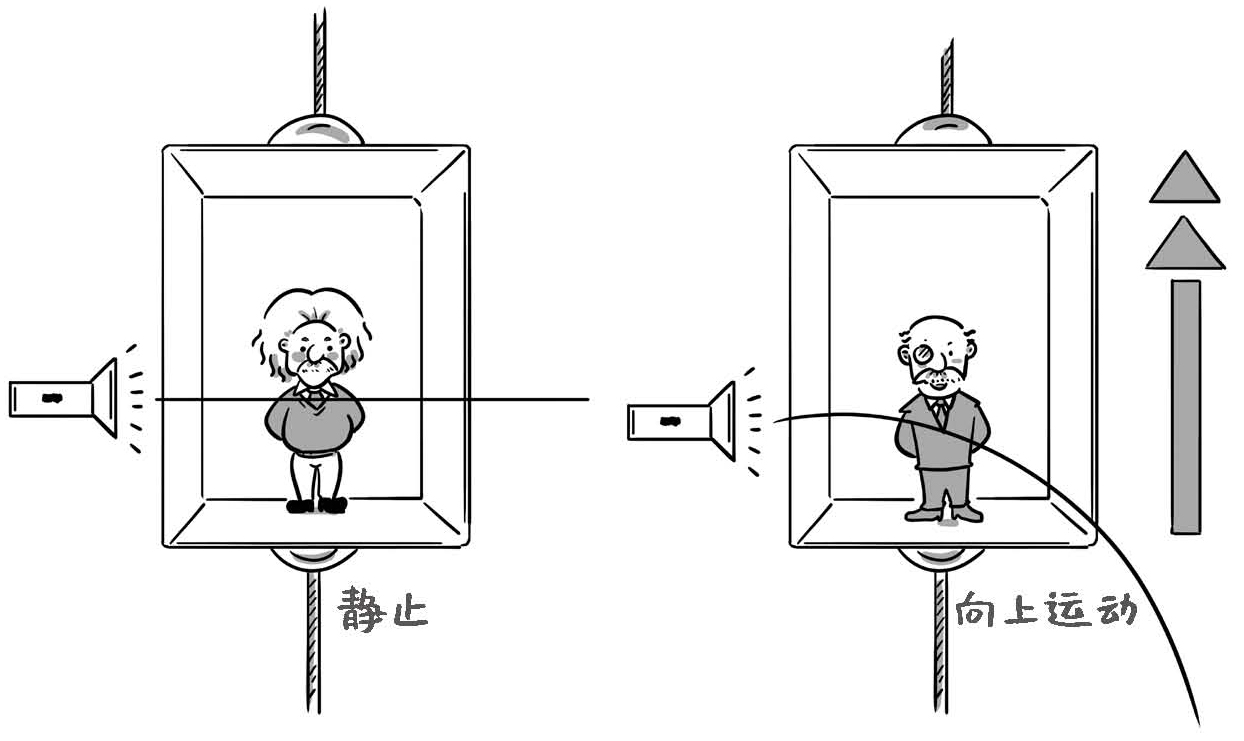
图7-5 电梯静止(左)和加速上升(右)
如果继续深入研究光从左边射到右边的过程,电梯里的人看这道光走过的路径应该是一条曲线,因为电梯在加速运动(如果电梯匀速上升,路径应该是一条向下的斜线)。所以,电梯里的人会感觉光转弯了,但是在电梯外的人看来,这道光走的仍然是一条直线。
下面等效原理就派上用场了。既然在加速上升的电梯里,人看到光走了曲线,那么同样地,如果在地球上做这个实验,光也应该走一条曲线。
光觉得自己在走直线
光在引力场的作用下会走一条曲线,也就是说,引力场对光也是有作用的。那这有什么神奇的效果呢?根据质能方程E=mc2,光是有能量的,所以它也有动质量(即运动时整体表征为质量的效果)。有质量的东西,就会在万有引力的作用下改变直线轨迹,走曲线不是很正常吗?
这里的关键在于,光并没有觉得自己在走曲线,它觉得自己还是在走直线。换句话说,在引力场的作用下,光并没有觉得自己受到了“引力”。
但是根据牛顿第一定律,一个物体在不受外力的作用时,要么静止,要么做匀速直线运动。光既没有受力,也没有进行匀速直线运动,这岂不是推翻了牛顿第一定律吗?问题出在哪儿呢?
问题就在于牛顿第一定律是不完备的,它讨论的是平坦的时空。光既不受到力的作用,而且走的还是曲线,这样就可以解释为引力场中的时空被扭曲了。这就好像火车在铁轨上行驶,火车的轮子是不会转弯的,它只知道向前滚,但是轨道可以弯曲。火车一直觉得自己在向前走,但实际上它已经随着轨道在走曲线了。
时空的扭曲也应该这样理解,在引力场中做自由运动、不主动给自己加速的物体,在它自己看来,它在走直线,符合牛顿第一定律,但是这条线本身却随着时空弯曲了。
进一步证明
时空的扭曲效果还可以被进一步证明。以后如果人类要移民到外太空,在太空中建造太空站,就需要在太空站里模拟地球的重力环境。但是在太空站里没有地球那么大质量的东西,要怎样模拟重力呢?答案是通过旋转产生的离心力(centrifugal force)。
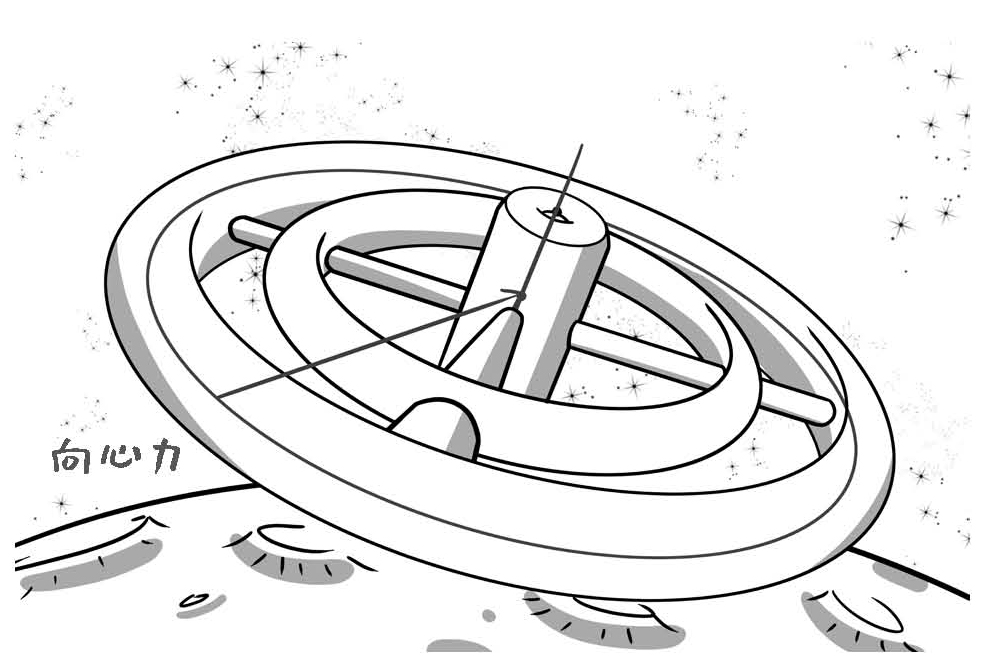
图7-6 太空站
太空站的结构在很多科幻电影中都出现过,譬如诺兰的《星际穿越》片尾,未来人类都移民到了太空站中,太空站里的人其实是住在一个大型的圆柱体的内表面。随着圆柱体围绕自己的中轴旋转,那么圆柱体内表面就要对太空站里的人提供支持力,来充当圆周运动的向心力。站在圆柱体内表面的人,跟感受到重力是一样的。
再对比一下另外一种情况:假设你现在在一个围绕地球做圆周运动的空间站工作,根据牛顿定律,你应该受到一个向心力,用以支撑你围绕地球的圆周运动,但是空间站里的人感觉依然是失重的。
现在假设上面说的人类移民外太空所住的旋转大圆柱体的直径跟地球是一样的,让它旋转的速度跟空间站围绕地球运动的速度是一样的。那么在这两种情况下,不管是空间站里的工作人员,还是移民到外太空的居民,他们的运动状态是完全一样的,都是以一定的速度在做圆周运动,并且运动的速度大小一样,圆周运动的半径也一样。但是他们的感受是完全不同的,在大圆柱体里的人会感受到圆柱体内壁的支持力,而在空间站里的人却感受不到力。
那么问题来了,根据牛顿定律,一旦运动方式确定了,受力情况应该是唯一的,怎么会出现运动状态完全相同、受力却不一样的情况呢?是不是牛顿定律错了?这里的解决办法就是时空的扭曲。在大圆柱里,时空并没有被扭曲,但是地球周围的时空被扭曲了。
这样就能解释为什么运动情况一样,受力却不同。地球周围空间站里的宇航员可以判断自己是在走直线,只不过这条牛顿定律意义上的直线被地球的质量弯曲成了一条曲线。
第四节 尺缩与钟慢
我们从等效原理出发,证明了引力不是一个力,只是时空扭曲的效果,这种扭曲是由质量造成的。置身于其中的物体感受到了时空的扭曲,于是运动状态发生了变化。这种运动的变化只是被牛顿解释为引力,但其实引力并不存在。
既然知道了时空可以被扭曲,那么扭曲的时空会带来哪些神奇的效果呢?很显然,狭义相对论里那些神奇的效果,比如尺缩效应和钟慢效应,在广义相对论中也是存在的。
尺缩效应可以理解为空间的压缩,钟慢效应也可以理解为时间的收缩。广义相对论既然说的是时空如何被扭曲,那对应的尺缩和钟慢效应也一定存在。只不过这次,我们可以从时空的扭曲出发来推论这些效果。
黎曼几何:曲面上的几何
首先要来探讨一个基本的问题:空间中两个点的距离是怎么算的?
我们都知道,两点之间直线最短。比如有一张平铺的纸,你在上面随意画两个点,然后用一根直线把它们连起来,那么这条线段的长度就代表了这两个点在纸面上的最短距离。
但是别忘了,这两个点的最短距离是一条线段,只在纸面是平面的情况下成立。如果是曲面,就未必如此了。比如在地球表面上任意取两点,在不穿透地表的情况下,两点之间最短的距离就是它们中间的那段圆弧,是一条曲线。
也就是说,在不同的空间当中,两个点之间的距离也是不一样的。既然广义相对论说的是时空的扭曲,那么两点距离的计算方式,就跟这个空间具体的扭曲形式有关了。研究曲面上几何关系的学科,叫作黎曼几何。

图7-7 地球经线,最后在极点处汇集为一点
在黎曼几何里,很多被欧几里得几何当成公理的东西是不成立的。比如说在欧几里得几何里,两条平行线是永不相交的,但这在黎曼几何里是不成立的。
我们知道,地球的经线和纬线都是相互垂直的。换句话说,任意两条经线是相互平行的。但是很明显,任意两条经线都会相交于南北两个极点。因此,黎曼几何是一套与欧几里得几何截然不同的几何学系统。
尺缩效应
有了对黎曼几何的认知,就能很容易理解在广义相对论下的尺缩效应和钟慢效应。
首先,要定义一个物理量,叫作时空曲率,它描述的是时空的扭曲程度。用万有引力的观点看,就是引力越大的地方,曲率(curvature)越大,时空扭曲的程度就越剧烈。
我们说时空的扭曲是被压缩,而不是被拉伸,是因为引力永远表现为吸引作用,而不是排斥作用。也就是说,有质量的物体倾向于靠近,而不是远离,只有压缩才会让距离缩短。质量越大的天体,对它周围时空的扭曲就越剧烈,它周围时空的曲率就越大。还是用一块海绵的弹性扭曲来看,质量越大,就好像压缩、扭曲海绵的程度越深。
那尺缩效应是什么呢?其实就是把空间当成一块海绵,再把它压缩成一个曲面。一把弹性尺上面有刻度,我们把它弯曲,当然是向里弯的部分被挤压了,尽管上面的刻度没有变,但是实际上,刻度之间的距离变小了,对应的就是尺缩,是空间的尺度变小了。此处要注意,是引力场弱的地方的观察者看引力场强的地方的观察者的空间被压缩,尺子的长度变短,但是尺子上的观察者并不会觉得尺子变短,因为在尺子参考系当中的所有尺度都同等地缩短了,因此尺子上的观察者自己是察觉不到的。
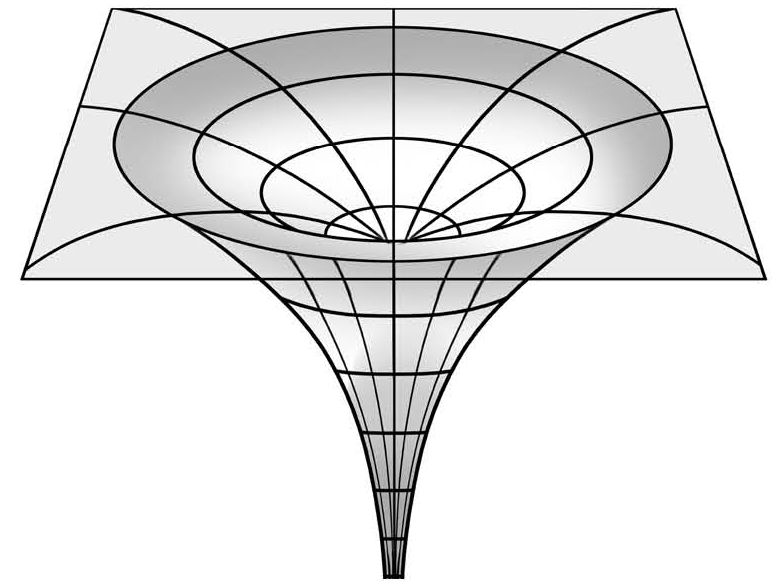
图7-8 黑洞周围的时空扭曲
钟慢效应
同理,也可以理解广义相对论下的钟慢效应。在“极大篇”中我们说过,时间和空间其实是等价的,不需要把时间和空间区别对待。
我们可以把时空当成一块海绵,只不过在它的长、宽、高三个维度中,高代表时间,长和宽代表空间。这种比喻只是为了方便理解,真实的情况应该是一个三维空间加上一维时间的四维的海绵。因为人的感官很难想象四维,这里就简化为二维空间加上一维时间。
这样,一块海绵在质量的作用下被压缩的时候,不光空间维度被压缩了,时间维度也被压缩了。本来一个事件持续的时间可能是2s,被压缩之后就只有1s了。
电影《星际穿越》里有一段剧情,男主角和女主角去一个黑洞周围的行星上探测。他们只去了3个小时,但是在飞船上的同事却等了他们20多年。这就是广义相对论里的钟慢效应。
因为黑洞边上的引力场极强,所以行星上的时间被压缩得非常厉害。这里还是要强调一下,当你进入一个强引力场范围内,只是别人看你的时间变慢了,别人掐表2s,在你这里才过了1s,但你不会感到自己的时间变慢。
双生子悖论的最终解释
有了基于广义相对论的对于尺缩效应和钟慢效应的理解,我们可以再回过头来讨论一下在“极快篇”中双生子悖论的问题。
假如有一对双胞胎兄弟,哥哥坐着一艘宇宙飞船以接近光速的速度,去太空里转了一圈,又回到地球上,而弟弟一直在地球上。问飞船回来以后,兄弟俩谁的年纪更大一些?
根据钟慢效应,由于哥哥的运动速度非常快,所以在弟弟看来,哥哥的时间流逝速度很慢。这样等哥哥回来后,弟弟经历的时间更长,所以哥哥反而比弟弟年轻。这样一个推论看似没什么问题,但是其中隐含着严重的逻辑矛盾。
虽然是哥哥坐着宇宙飞船去宇宙里转了一圈,但是在哥哥看来,何尝不是弟弟在地球上,地球相对于哥哥坐的宇宙飞船,也以接近光速的速度转了一圈?因为运动完全是相对的,无论是哥哥还是弟弟,都会觉得自己是不动的,是对方在运动,所以对于哥哥来说,应该是弟弟的时间流逝速度更慢。自己回地球以后,应该更加年老。
这个问题需要借助广义相对论才能回答。因为是哥哥坐着宇宙飞船出去转了一圈,那么很显然,哥哥经历了有加速度的过程。他要先加速飞出去,然后回地球的时候还要减速,减速的过程可以看成是反向的加速。根据等效原理,哥哥经历了等效于置身强大引力场的过程,所以他的时间受到了压缩。回来之后,应该是哥哥更加年轻了。
第五节 引力红移
哈勃定律告诉我们,宇宙是在加速膨胀的。哈勃给出这个结论的方法,是通过多普勒效应和光谱,算出了天体的距离和远离我们的速 度。
一个正在远离我们的天体发出的光,被我们接收到的频率要比它原本的频率低,这种现象叫作多普勒红移。除了信号源和接受者有相对速度会产生多普勒效应以外,引力场也会产生广义的多普勒效应,这恰恰是可以用等效原理解释的。
宇宙中有各种各样的天体,这些天体都会在自身周围形成引力场。光经过这些引力场的时候,也会经历红移或者蓝移。如果从地面上垂直向上发射一束光给太空中的接收器,接收器接收到的光的频率,要比从地面上发出时的频率低一些,这是为什么呢?
这里依然要用到等效原理。现在想象两艘宇宙飞船,一前一后,它们同时加速向前运动,中间保持一段距离。前面的飞船尾部有一个光学接收器,然后让后面的飞船向前发出一束光,这束光会被前面飞船的接收器探测到。
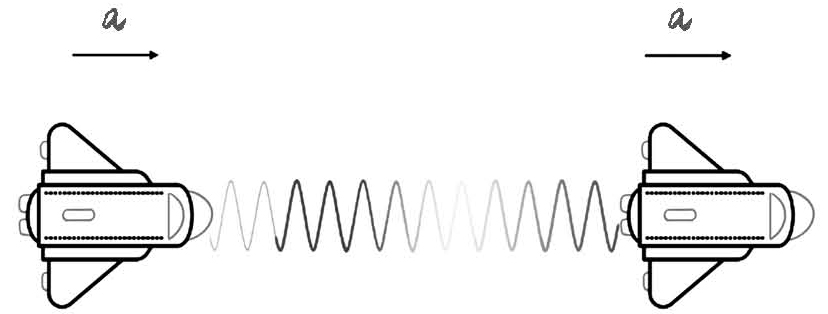
图7-9 由加速产生的红移/蓝移(后方飞船向前发射的信号在前方飞船的接收者看来频率降低,由前方飞船向后发射的信号在后方飞船接收者看来频率增高)
由于这两艘飞船有一段距离,所以当后面飞船那束光被前面飞船的接收器接收到的时候,已经经过了一段时间。但是由于飞船有加速度,前面的飞船在这段时间里,已经增加了一定的速度,此时,对于前面的飞船来说,这束光的光源不再是相对静止的了,而是有一定的速度。既然有速度,就会发生多普勒效应。因此,前面的飞船接收到的光的频率,要比光发出时的频率更低。反之,前面飞船向后方飞船发射信号,在后方飞船看来,这个信号则会发生蓝移。分析过程也一样,还是看两艘一起加速的宇宙飞船。只不过这次让前面的飞船向后发射光,后面的飞船装了接收器。在光到达后面的飞船时,已经过了一段时间,这样后面的飞船就增加了一定的速度。在后面的飞船看来,光源是在向自己靠近。根据多普勒效应,它接收到的光就发生了蓝移。
上面已经证明了,在有加速度的情况下,光会发生红移和蓝移。那么根据等效原理,在地球上,或者说在任何一个引力场中,光也一定会发生相应的红移和蓝移。
所以,从地球上向上发射一束光,太空里的接收器一定会接收到一束经历了引力红移、频率变低的光。反过来是一样的,如果从太空发射一束光给地面上的接收器,地面上接收到的光频率会更高,光发生了蓝移。
本章主要从理论层面去了解广义相对论。广义相对论最具革命性的观念是重新理解了引力。引力并不是一个真实的力,只是质量扭曲了时空,从而影响了物体的运动。
广义相对论和狭义相对论一样,只依据一条简洁、优美的原理,来进行逻辑的演绎,可以说是真正的理论物理学。相对论让我们深刻地体会到思想之美,所以爱因斯坦不光是一位天才的物理学家,也是真正意义上的思想家。
