标准模型
第一节 粒子之间如何相互作用
粒子物理在一定程度上把所有基本粒子的种类都辨别清楚了。组成重子和介子的基本粒子都是夸克，夸克总共有36种（3色、6味、正反粒子，3×6×2=36），它们无法独立存在。夸克有色荷、味荷和电荷。其中色荷能够发生强相互作用，味荷发生弱相互作用，电荷用来发生电磁相互作用。它们都有质量，可以发生引力相互作用。味的种类决定了夸克的质量。它们的质量从小到大，分别是上夸克、下夸克、奇异夸克、粲夸克、底夸克、顶夸克。
夸克是可以发生全部四种相互作用的基本粒子。除了夸克以外，轻子也有6种，分别是电子、μ粒子、τ粒子，电子中微子、μ中微子、τ中微子以及它们的反粒子。其中，电子、μ粒子、τ粒子带电，这三种粒子对应了三种不带电的中微子。这三种中微子的质量并不精确为零，但十分接近零，所以它们参与极其微弱的引力相互作用，除此之外，它们只参与弱相互作用。
夸克模型的遗留问题
如此看来，我们已经在实验室里发现了众多粒子，粒子物理对于粒子种类的研究已经相当成功了。但是，目前人类对它们的理解还不够彻底。还记得在“极重篇”第七章《广义相对论的基本原理》的开篇就提出的两个问题吗？
（1）万有引力具体是如何作用的？
它们看似没有作用的媒介，后来我们知道，这种媒介就是时空本身。
（2）引力的作用是不是超距作用？它的传播是否需要时间？
根据广义相对论，引力的作用不是超距的。它的传播速度，或者说时空扭曲情况的传播速度，等于光速。
夸克之间的色，是发生强相互作用的关键，味是发生弱相互作用的关键，电是发生电磁相互作用的关键。同样地，我们可以提出这些问题：这三种相互作用的作用机制是什么？它们作用的媒介是什么？它们的传播是否需要时间？
经典物理是怎么解释相互作用的？
经典物理中对相互作用，譬如电磁相互作用和引力相互作用，是用电磁场以及引力场的概念去描述的。可以回顾一下中学里是怎么学的，一个电荷会在它周围建立起电场，这些电场可以用电场线来表示。电场线密度高的地方表示电场强度大，反之则表示电场强度弱。磁场也可以用类似的磁场线来表示。
但仔细一想你就会发现，这种场的表述方式，在微观层面上是不抓本质的。电场线、引力线的概念其实是人为创造出来的，我们无法用任何实验来证明有电场线、磁场线的存在。
我们之所以会创造这样的概念，完全是为了方便理解和计算。比如为了了解一个电荷产生的电场，可以用一个检验电荷放在它周围的任何地方，并记录检验电荷在这些地方感受到的力的大小和方向，再根据每个位置受库仑力的大小和方向，人为地加上电场线的概念来描述检验电荷放在被检验电荷周围时所受库仑力的情况。
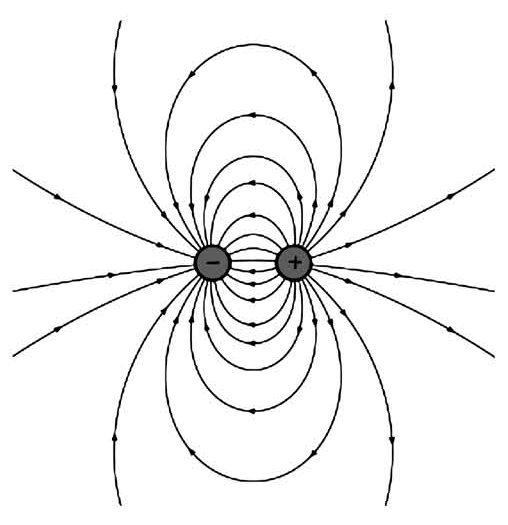
图14-1 一个正电荷与一个负电荷的电场线
经典电磁学认为电磁场是连续的，但由于微观物理世界是量子化的，因此用经典的观点来解释是不抓本质的。基本粒子的相互作用，应当时时伴随着量子力学的规律。比如，不确定性原理永远应该摆在首位，光这一条，你就会发现其实稳定连续的电场在微观的时空尺度上根本不可能存在，因为如果要满足不确定性原理，电荷不可能处在位置和速度都确定的状态。即便我们依然沿用库仑定律描述一个电荷产生的电场，它在微观层面上也不可能产生一个静止、稳定且连续的电场。因此，我们需要重新定义相互作用的本质。连续的经典场表述，在量子系统的层面上，尤其是小到夸克这个尺度就太粗糙了。
什么是力？
粒子物理对于相互作用的定义，其基本思想还是从实验出发，用测量到的物理量对量子系统进行描述。这里能测量到的无非就是基本粒子的各种性质，比如电荷、质量等。也就是说，我们能测量到的无非就是粒子的各种物理性质的集合，这些集合定义了不同种类粒子的存在。
在粒子物理层面，如果一种相互作用的本质是交换了粒子[此处还应包含“虚粒子”（virtual particle）]，我们就说这种相互作用是一种力。譬如，电磁力的本质是电荷之间交换了光子。
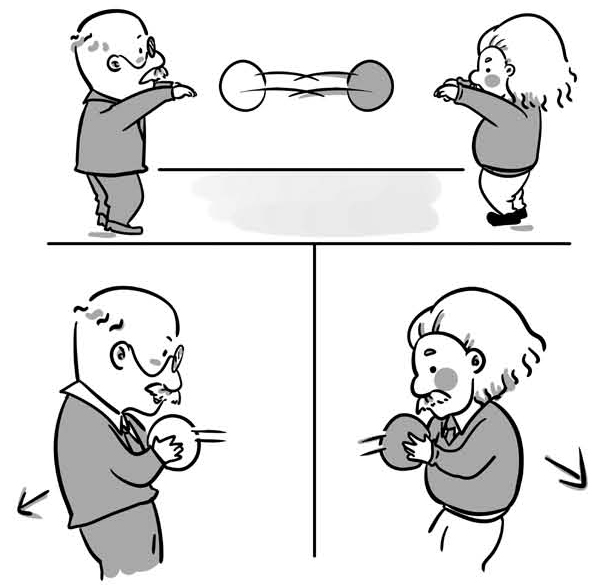
图14-2 爱因斯坦和普朗克的铅球游戏
举个例子，爱因斯坦和普朗克两个人穿着溜冰鞋站在冰面上，每个人手上都抱着一个铅球，现在他们把铅球都扔给对方，同时接住对方扔给自己的铅球。在这个过程中，他们交换了手中的铅球。可以想象，他们在抛出和接到对方铅球时都会向后退，从宏观上看，他们之间就像产生了排斥力一样，但是他们每个人和铅球作为一个个体，都没有发生变化。
这就是粒子的交换，产生的效果等同于受到了力的作用。
引力到底是不是力？
明确了力的本质是粒子的交换，接下来就要研究目前已有的四种相互作用：色荷产生的强相互作用、味荷产生的弱相互作用、电荷产生的电磁相互作用，以及质量产生的引力相互作用，看看它们之间有没有粒子的交换。如果有，交换的粒子是什么？它们的性质是什么样的？
强相互作用、弱相互作用和电磁相互作用都交换了粒子。强相互作用交换的是胶子，胶子有8种，并且每一种胶子都是自己的反粒子。弱相互作用交换的粒子有3种，分别叫作W+、W-、和Z0粒子。其中W+和W-互为反粒子，Z0是自己的反粒子。电磁相互作用交换的是光子，光子也可以被认为是自己的反粒子。这些用来交换的粒子，都是玻色子，自旋都是1。
根据爱因斯坦的广义相对论，引力只表现为时空的扭曲，它并非一种力，但这只是宏观上的解释。要判断引力在微观层面上是否是一种力，要看它是否交换了粒子。有很多理论认为引力如果是一种力，它交换的应该是引力子（graviton），引力子也是玻色子，并且根据引力只体现为吸引，并无排斥的效果，以及量子场论的理论预测，引力子的自旋应当为2。但引力实在太弱，引力波如此宏观的现象都那么难以探测，更不要说是微观的引力子了。
这里有很多新的概念，比如胶子、W+、W-和Z0玻色子等。我们接下来的任务就是去研究这些用来交换的粒子到底是什么，它们是怎么产生的，它们的性质是什么，这就进入了一个新的领域——量子场论。
第二节 守恒量（conserved quantity）与对称性（symmetry）
现在，我们已经在粒子物理的层面，清楚了36种夸克和12种轻子，它们之间是有相互作用的。
由于引力太弱，引力强度大约是弱力强度的1/1029，所以此处先不关注引力。力的本质被定义为粒子的交换。我们现在的目标是把36种夸克、12种轻子，以及它们之间用以交换的粒子统一到一套理论框架中。因为物理学的任务是追求终极，既然是终极，就要寻找最基本、最统一的道理。粒子的种类既然有这么多，就预示着一定有更基础的理论去解释它们。
我们把夸克、轻子以及力的定义作为归纳性的起点，在这个基础上进行演绎，用一套理论把它们之间的相互作用解释清楚。这就像研究原子的过程：先清楚了原子的组成结构是电子和原子核，下一步就是研究电子和原子核的关系，以及它们的运动状态。认识了最基本的夸克和轻子，下一步就是将其统合，研究它们的相互作用力，这就需要用到量子场论的知识。
为了理解量子场论，我们要先做一些知识铺垫，那就是守恒量与对称性的关系。
诺特定理（Nöther theorem）
我们在前面已经讲到过很多守恒的概念了，比如能量守恒、动量守恒、角动量守恒、电荷守恒等。在一个变化或者反应的前后，那些不变的量叫作守恒量。
除了守恒量以外，还有一个概念叫对称性。什么是对称性呢？中学里其实都学过类似的概念，比如：将一个正三角形旋转120°、240°或者360°，这个三角形都能转回去；将这个三角形沿自己的对称轴进行翻转，也能翻转回去；一个圆围绕它的圆心不管转多少度都还是跟原来一样的一个圆。一个对象在某个操作下，原本的状态不发生改变，我们就说这个对象具有某种操作下的对称性。
对比守恒量和对称性的描述，可以发现它们很像。守恒量是指变化中不变的量，对称性是指操作中不发生变化的性质。总的来说，都是变化了之后不变的东西。
20 世纪初，一位德国的女性数学家诺特（Emmy Nöther）提出了诺特定理，它可以说是划时代的伟大定理。它直接奠定了所有场论的基础，不论是经典场论，还是量子场论。这条定理说的事情十分简单，就是对称即守恒。它把守恒律和连续对称性完全等价了，也就是说，任何一条守恒律的背后，都对应着一种连续对称性，反之亦然。（注：所谓连续对称性，就是在对对象做操作的时候，这种操作所带来的变化必须是连续的，譬如移动一个物体，它的位置的变化必须是连续的。因此上述案例中，让一个正三角形作120°、240°转动，这样的非连续对称性，并不对应守恒量。）
这样说还是太抽象了，我们来举几个例子。
空间平移对称性：动量守恒
先看动量守恒，动量守恒对应的是空间平移对称性。比如有一个物理系统，这个物理系统里的动量是恒定的，你把它从上海拿到苏州，这个系统的动量是不变的，也就是上海和苏州的空间性质几乎是一样的，所以动量是守恒的。但是，如果把系统移动到太空中就不一定了，因为太空中的引力和地球表面不一样，时空扭曲的程度不一样。
空间平移对称性说的就是在移动的过程中时空的扭曲程度没有发生变化。如果从一个平坦的时空移动到一个扭曲的时空，空间平移对称性被打破，动量守恒定律就失效了。
时间平移对称性：能量守恒
能量守恒定律对应的是时间平移对称性。时间平移对称是指：不管时间怎么流逝，物理定律不变。比如所有物理定律三百年前是这样的，三百年以后也还是这样。然而所有的物理定律都显性地或隐性地跟能量有关联，所以物理定律不随时间变化而变化，本质上对应的是能量守恒定律。这也是诺特定理通过数学推导得出的直接结论。
镜像对称性：宇称守恒
在一个正三角形前放一面镜子，镜子里的正三角形跟镜子外面的正三角形是一样的，这叫镜像对称。镜像对称对应的守恒量，叫宇称（parity）。这个概念跟我们中学里学过的奇函数和偶函数的概念很像。一个偶函数图像是左右对称的，我们就说它的宇称是1。一个奇函数，比如y=x³，它的图像左右不对称，而是刚好相反，就说它的宇称是-1。
镜像对称性对应的守恒量是宇称。也就是说，如果原本的研究对象（比如量子系统的波函数）宇称是 1，它的镜像图像的宇称一定是1；如果你的波函数宇称是-1，再构造一个与它完全成镜像的物理系统，其对应的波函数的宇称也一定是-1。
广义地来说，宇称守恒说的是，物理定律不分左右，给任何物理过程做一个镜像系统，这个镜像系统里的物理定律应当跟原系统是一样的。
宇称不守恒定律
说到宇称守恒，不得不谈一下由杨振宁和李政道于1956年提出的宇称不守恒定律。宇称不守恒定律说的是：在弱相互作用的过程中，宇称是不守恒的。
宇称不守恒定律的提出，最早是因为一个粒子物理学中的难题，叫作“τ-θ问题”（tau-theta puzzle）。有两种奇怪的介子，当时叫τ介子和θ介子，这两个介子的所有性质几乎都完全一样，如它们有同样的质量、电荷量、自旋等。唯独它们在发生衰变时，衰变的结果是不一样的，τ介子会衰变成另外三个介子，而θ介子只会衰变成两个介子。
杨振宁和李政道提出，因为在弱相互作用过程当中，宇称是不守恒的，所以这两种粒子其实根本就是同一种粒子，现在我们知道了它叫K+粒子，只不过它以两种衰变方式的其中一种衰变，前后宇称是不守恒的。
如何理解呢？假设现在有一面镜子，根据生活经验可以想象一个波函数照镜子，它会在镜子里看到一个镜像的波函数。根据直觉，镜像的波函数应该跟镜子外的波函数拥有一样的宇称。如果波函数是个偶函数，那么镜子里的波函数也应该是个偶函数；如果波函数是奇函数，那么镜子里的波函数也应该是个奇函数。感觉上这是一个理所当然的结论。
宇称不守恒定律认为，在弱相互作用过程中，宇称不守恒。就好比本来是个偶函数，照了一下镜子就变成奇函数了。再举个例子，有一辆正常的汽车，踩下油门车就会往前走。这时在车边上放一面镜子，镜子里的汽车是镜子外汽车的镜像。根据直觉，踩油门让汽车往前走的时候，镜子里的汽车也应该是往前走的。但是宇称不守恒说的就是踩油门的时候，你的车子确实往前开了，但是镜子里的汽车却是倒着开的。
这是一个非常反常识、反直觉的结论，所以宇称不守恒定律刚被提出的时候，学界的主流声音是表示反对的。泡利甚至说：“我不相信上帝是左撇子。”泡利认为这个宇宙里的物理定律是不分左右的，左和右应该是完全对称的。但是，宇称不守恒定律似乎在告诉我们：这个宇宙里的规律是分左右的。
宇称不守恒定律很快就被吴健雄用实验证明了。这个实验不好做，但是原理很简单。这个实验研究的是钴-60的β辐射，因为β辐射就是弱相互作用主导的。先让钴-60原子在某个特定的磁场里排列，这些钴-60原子的自旋指向在磁场作用下是沿着磁场方向排列的。再准备另外一些钴-60原子，在另外一个与先前磁场反向的磁场里排列。由于这次的钴-60原子的磁场跟刚才的方向相反，所以它们的自旋也是相反的。从旋转的视角来说，两组钴-60原子分别是顺时针和逆时针旋转的。对比一下，会发现顺时针和逆时针旋转的钴-60原子，刚好形成了互为镜像的两种钴-60的排列，这个镜面方向就是磁场的方向。
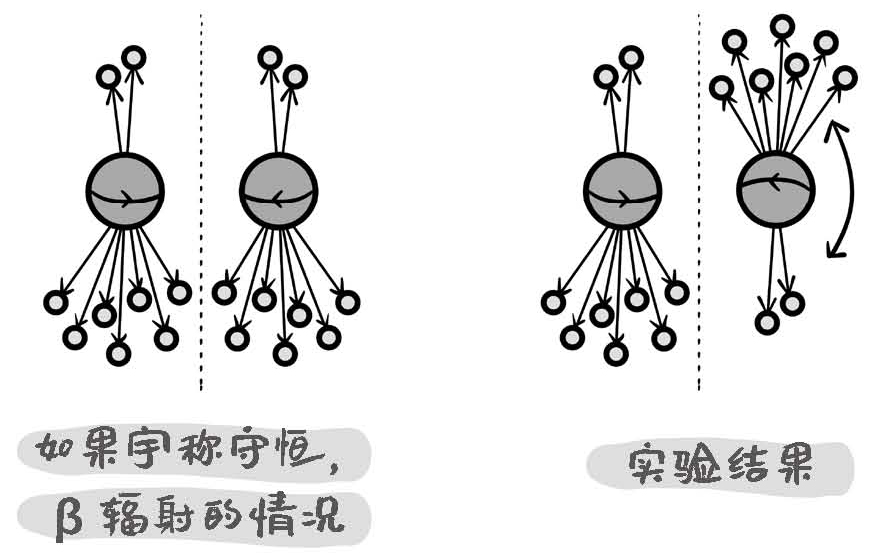
图14-3 宇称不守恒定律下的β衰变
不信你可以试着看一下，你的手表指针是顺时针旋转的，但是镜子里的手表指针是逆时针旋转的。根据刚才汽车的例子，如果宇称守恒，汽车前进，镜子里的汽车也应该前进。钴-60 会发生β衰变，由于磁场的存在，它的β辐射应该平行于磁场方向，也就是跟镜面平行。如果宇称守恒，不管顺时针还是逆时针的钴-60的β辐射都应该是同一个方向的。但是实验结果却令人惊讶，顺时针和逆时针的钴-60的辐射方向居然刚好相反，就好像一辆前进的汽车的镜像居然是后退的，这就充分证明了弱相互作用中的宇称不守恒。
上帝是左撇子：左旋性中微子
中微子的一个神奇特性充分证明了弱相互作用中的宇称不守恒，那就是中微子的螺旋性（helicity）。中微子的螺旋性可以说是让泡利对宇称不守恒定律的那句评论一语成谶，看来上帝还真是个左撇子。
先来说说什么是螺旋性。我们知道，中微子的静质量极小，几乎接近于零，因此在各种反应中产生的中微子的运动速度非常接近光速。我们可以沿着中微子的运动方向建立一个坐标轴，定义中微子的运动方向为z轴的正向。中微子是费米子，自旋是1/2。我们可以尝试测量中微子沿着z轴方向的自旋是指向z轴正方向还是沿着z轴负方向。如果中微子在z轴方向上的自旋指向是沿着z轴正方向，我们就说这个中微子的螺旋性是右旋（right-handed），相反，如果中微子在z轴方向上的自旋指向是沿着z轴的负方向，则中微子的螺旋性是左旋（left-handed）。
神奇的是，就目前来说，在实验里探测到的所有中微子都是左旋中微子，所有反中微子都是右旋中微子。中微子不带电，没有色荷，除了引力之外，中微子只参与弱相互作用。生成中微子的反应，都是弱相互作用主导的，如β衰变中，中子衰变成质子，并放出一个电子和一个反中微子。也就是弱相互作用中宇称确实不守恒，如果宇称守恒的话，弱相互作用中应该产生等量的左旋中微子和右旋中微子，但是事实是，弱相互作用只偏好左旋中微子。这恰恰说明，宇称不守恒是弱相互作用的一个基本特性，弱相互作用的物理规律是个区分左右的物理规律。
其实中微子的螺旋性也回答了一个问题，就是如何区分中微子和反中微子。在β衰变中，我们怎么知道产生的是反中微子而不是中微子？中微子不带电，也没有色荷，中微子和反中微子质量相同，也没有电荷、色荷的区别，如何区分正反？这里的螺旋性就是一个区别，它们必然具备相反的螺旋性。
实验确定中微子的手性其实也很有趣，我们其实无法直接探测中微子的自旋方向，因为它不带电，无法参与电磁相互作用。中微子的手性测量是间接测量。一个π+介子可以衰变成一个反μ粒子和一个μ中微子。π+介子的自旋是零，反应前后系统总自旋不变，μ粒子和反μ粒子是带电的，所以我们可以通过测量反μ粒子的自旋来推理中微子的自旋方向，从而得出中微子的手性。
正是因为宇称不守恒定律的结论太反常识，且纠正了学界长久以来的错误认知，所以在1957年，论文发表一年以后，杨振宁和李政道便获得了诺贝尔物理学奖。
总而言之，诺特定理让对称性对应了守恒量。接下来，我们来看看粒子物理当中那些守恒量到底是怎么来的。为什么电荷是守恒的？它背后对应的是一种对称性——规范对称性。
第三节 规范对称性与规范场（gauge field）
阐明了守恒量与对称性的关系，要如何理解这些基本粒子之间不同的作用力呢？它们交换的粒子之间的关系是什么样的呢？
什么是量子场？
不管这些基本粒子交换的是什么粒子，如何交换，我们先把基本粒子，也就是夸克、轻子当成一个整体来研究，它们都应该满足量子力学。
原子里的电子，它们的运动范围小，且数量不多，可以用薛定谔方程去研究一个电子的运动情况。但是在一般情况下，我们感兴趣的是广义上由多个粒子组成的量子系统的整体性质。先不从粒子交换的物理过程去理解粒子之间的相互作用，可以先把粒子之间的相互作用抽象成一根根弹簧。可以想象，粒子和“弹簧”系统织成了一张大网。
这张大网有弹性，上面还存在波动，有各种运动模式。但与一张普通的弹性网不同，这里所有的粒子都是量子化的，它们都要满足不确定性原理。所以这张网上代表一个粒子的并不是一个点，而是一团波函数。这团由波函数组成的巨大网格，就是量子场。场是一个数学概念，场的定义是以时空坐标为自变量的函数。
量子场论是需要融入狭义相对论的，我们知道，根据质能方程E=mc2，能量与质量可以互相转化，因此薛定谔方程中有一个条件在考虑狭义相对论的情况下就未必成立了，那就是粒子波函数的归一化条件。还记得我们在量子力学的章节中讲到，波函数的分布代表粒子在全时空范围中任何一个位点出现的概率密度，但是如果把整个时空范围的所有概率加起来必然等于1，因为这个粒子存在，所以在全时空范围内必然能够找到它，这个“必然”就使得它在全时空范围被找到的总概率是100%，即1。但如果考虑了狭义相对论，粒子的质量可能转变为能量，因此归一化条件未必成立，这也导致薛定谔方程不足以描述相对论性粒子的量子规律。量子场论是广泛意义上统一讨论粒子物理的必备工具。
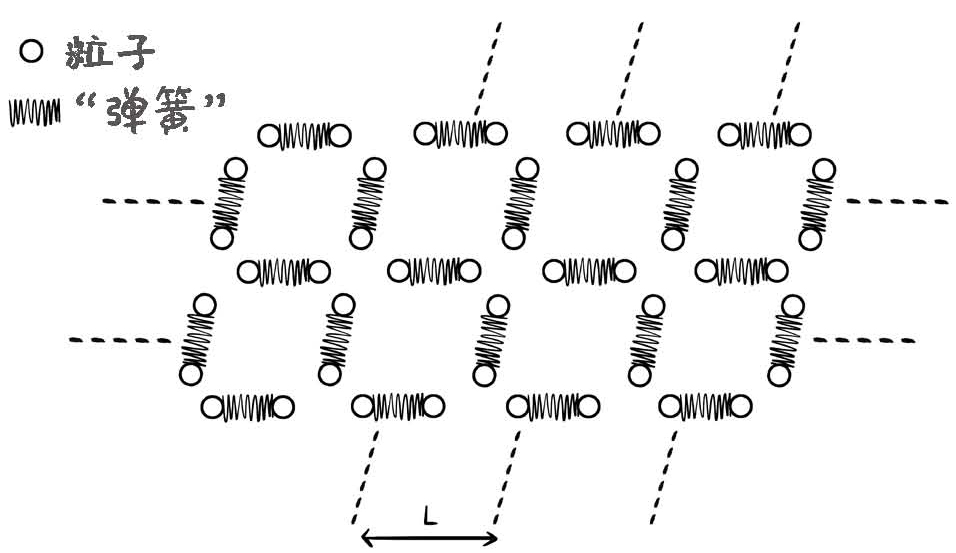
图14-4 量子场的物理图像
杨-米尔斯场
量子场这张大网里的“弹簧”是什么做的？它的性质是什么？我们现在对量子场还是一无所知，得到的一些归纳性的结论其实就是一系列守恒量。比如，量子化的电磁场必须保证电荷守恒，由诺特定理可以知道，这种守恒必然对应于某种对称性。于是，这里的思路就变成：找出对应于守恒量的对称性，从对称性出发，了解量子场中“弹簧”的性质。
这就要说到著名的规范场论，也叫杨-米尔斯理论。该理论于1954年由杨振宁与罗伯特·米尔斯（Robertmills）共同提出。它的基本思路相对比较复杂，需要一定的数学知识才能明白。
这一切还要从波函数说起。先前一直说量子系统的波函数代表了粒子出现的概率。波函数的数学表达式，可以是一个复数。高中的时候，我们学过一个概念——虚数i，它被定义为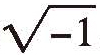
，即 i2=-1。复数就是一个实数加一个虚数，复杂的数的意思。实数代表可测量值，比如测量一个东西的大小、高低、快慢、质量、电量等，这些物理量都是实数，而虚数是一种人造数字，它没有实际意义，至少自然中没有任何可测的物理量可以用虚数表示，我们做实验得到的结果必须是个实数。我们的实验测量在数学公式上的表达，对应的是对波函数这个复数做各种数学操作，并且要保证操作完之后得出的结果是个实数，否则这个结果没有物理意义。
我们说波函数表征了粒子出现概率的大小，这个说法其实没有完全说完，应该是波函数的“模”（modulus）的平方大小，正比于粒子处在某状态的概率的大小。比方波函数是 a+bi，其中 a 和 b 是实数，i 是虚数。这个波函数本身不能代表概率，而它的模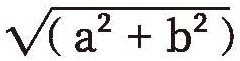
是实数，这才是一个有意义的数字。
既然如此，只要最终算出来的a2+b2不变，那么不管波函数是a+bi，还是a+bi 乘以一个模是1的复数，都不影响最后概率的大小。在保持最后测量结果不变的情况下，我们可以任意选取波函数的形式，因为最终测量的只能是和波函数的模相关的物理量。在保持模不变的情况下，可以选取无数种波函数的表达式来表达同一个状态。
这里就出现了对称性的特点。我们对波函数做的操作，就是在保证模不变的情况下，可以任意变换它的波函数。每次变换都不会改变对它的测量结果，这就是一种对称性，叫规范对称性。同一个物理状态，可以用无数个波函数去描述它，这里的每个波函数都是一个规范。但也不是所有波函数都可以，必须满足一定的条件。比如，对于描述电荷的波函数来说，条件就是波函数不管怎么变，模不能变。这就好比你给孩子取名字，你可以给他取无数名字，但是为了让别人从名字里看出来它是个中国人，你总归要用汉字给他取名字。这里的无数个名字，就是你孩子的无数个规范。必须用汉字，就是给一个中国孩子起名字的规范对称性。
与前面我们说的对称性（如空间平移对称性、时间平移对称性）不同，规范对称性不是一种时空对称性，它是微观粒子内部的内在对称性。一个量子场必须满足整体的规范对称性，也就是整个量子场的不同时空位置，如果同时发生一个规范的变换，不会影响系统的任何性质，因为最终取的是波函数的模。就好比全中国人都改名，大家全都在原来的名字面前加个“王”字，不会影响大家分清楚谁是谁。
但这明显是不够的，因为量子场的相互作用是局域化（localized）的。两个粒子在 A 地发生相互作用，肯定不会马上影响到几光年以外的粒子的行为，所以，规范对称性不应该是整体、全局的对称性，而应该是局域化的。也就是说，在量子场中，每一个电荷的波函数都应该能自由选取一个规范。一个地方换了规范，并不会影响全局。就好比你给自己的孩子取名字，不用管邻居给他的孩子取什么名字，这叫局域规范对称性。一旦要求量子场的波函数必须满足局域规范对称性，神奇的事情就发生了。
如果要满足局域规范对称性，就会发现必须有一个额外的量子场存在，这个场就是规范场。如果只研究电荷，我们会发现，为了满足局域规范对称性，必须存在电磁场。也就是说，电磁场在量子力学的框架内，无非就是电荷波函数的规范场而已。电磁场的存在，是被局域规范对称性牢牢约束的。
原本我们对电磁场的理解是归纳性的，我们用实验发现存在电磁场，但是有了规范场，我们就把归纳法的源头推到了局域规范对称性。局域规范对称性是归纳的第一性原理，为了满足局域规范对称性，必须存在一个规范场，这个规范场在物理性质上就体现为电磁场。也就是说，电磁场成了局域规范对称性演绎的必然导出。
那如何理解电磁相互作用呢？电磁相互作用只是这个规范场的扰动而已。什么是扰动？就是让规范场的能量往上提升一个单位，激发规范场的能量单位提升一个单元，就出现了一个规范玻色子（gauge boson）。
规范场就像一盆肥皂水，你搅动一下，它就会产生泡沫。这些泡沫叫作规范玻色子，它们就是基本粒子之间相互交换的粒子。到这里其实就可以回答这些基本粒子是如何相互作用的了。
这里要换成对称性的语言。色荷、味荷、电荷，这三种荷的本质并非因为测量得出它们是三种不同的荷，只不过它们的波函数对应于三种不同的局域规范对称性，这就要求存在三种不同的规范场。就像一盆肥皂水，这三种荷的作用就是在肥皂水里搅动起三种不同的肥皂泡。这些荷之间交换肥皂泡导致的效果，体现为它们之间的作用力。
这三种对称性是用数学中的群论来描述的，具体的是用群论中的李群（Lie group）进行描述的。它们都有不同的名字，电磁场是U（1）规范场，弱力场是sU（2）规范场，强力场是sU（3）规范场。这三种对称性的数学性质完全不同，其中sU（2）、SU（3）是真正的杨-米尔斯场。
这三种规范场的“肥皂泡”，到底是什么呢？
U（1）规范场被激发起来的“肥皂泡”就是光子。SU（2）被激发起来三种粒子，分别是W+、W-和Z0玻色子，其中W+带正电，W-带负电，Z0不带电。SU（3）被激发起来的是胶子，胶子本身携带色荷，传递强相互作用力。这些用来交换传递的粒子，都是玻色子，具体地，它们被称为规范玻色子。
根据诺特定理，这几种规范对称性对应的守恒量都可以计算出来。算出来的结果自然而然就有各种各样的守恒量。例如，U（1）规范场用来描述电磁相互作用，它的规范对称性给出了电荷守恒。其他规范场的守恒量相对复杂，但是都很好地解释了为什么会有那么多守恒量。
渐进自由（asymptotic freedom）
杨-米尔斯理论可以说是一个极具美感和根基性的强大理论。我们之前谈过夸克禁闭，是指无法分离出独立的夸克。夸克禁闭作为一种现象，目前虽无确定的理论解释，但依据杨-米尔斯理论的研究所得出的“渐进自由”，却比较好地佐证了夸克禁闭这种现象。
首先我们来看一个简单的问题。我们知道，在经典电磁学中，两个电荷之间的库仑力正比于二者电荷量的乘积，反比于二者距离的平方。现在想象让两个电荷之间的距离开始缩小，库仑力的形式告诉我们，随着二者距离不断趋近于0，库仑力的大小将趋向于无穷大，这就说明经典电磁学库仑力的数学形式是无法精确描述微观尺度下电磁相互作用规律的，因为两个电荷距离为零这个点，是库伦定律这条物理定律的“奇点”，库仑定律在电荷距离趋近于0的情况下破溃了，要描述电荷距离极小的情况，必须要对库仑定律进行修正，这说明库仑定律不是最根本的描述电磁相互作用的理论。
以夸克和胶子为研究对象，研究强相互作用的学说叫量子色动力学（quantum chromodynamics），色动力学是用SU（3）杨-米尔斯场对强相互作用进行描述的。如果两个夸克之间的距离极其接近，夸克之间的作用力也趋向于无穷大的话，也就是假如SU（3）杨-米尔斯场也遇到了上述类似于库伦定律的问题，则说明杨-米尔斯理论也不够有根基。但在1973年，美国物理学家韦尔切克（Frank Wilczek）、格娄斯（David Gross）以及波利策（David Politzer）发现的SU（3）“渐进自由”现象，恰恰证明了杨-米尔斯理论是根基性的理论，因为“渐进自由”现象告诉我们，杨-米尔斯理论根本不会遇到类似于库仑定律那样的破溃。
渐进自由的结论其实很简单：当夸克之间很接近的时候，它们的相互作用非常弱，直至夸克之间的距离趋向于0，它们的相互作用强度也趋向于0，相反，当夸克之间远离的时候，它们的相互作用变得强烈。这个结论让夸克禁闭显得自然，当夸克之间的距离增大的时候，强相互作用的趋势是阻止它们的距离变得更大。三位提出渐进自由现象的物理学家于2004年获得了诺贝尔物理学奖。
渐进自由现象凸显了杨-米尔斯理论的根基性与普适性。
从逻辑上应该如何理解杨-米尔斯场的思想呢？我们用实验测量出电荷、色荷、味荷的存在，本质上是对其存在的一种归纳性理解。但是规范场论告诉我们：电荷之所以表现得像电荷，色荷之所以表现得像色荷，是因为它们以波函数存在的具体形式，满足了不同的规范对称性。
规范场论把我们对于各种荷以及基本作用力的理解，又推进了一层，这几种荷以及它们的相互作用其实是可以用演绎法推出来的。规范场论告诉我们，力源自对称。
至此，我们了解了如何用规范场（也就是杨-米尔斯场）理论理解这些基本粒子之间的相互作用，以及它们是如何被统合到同一个理论框架内的。然而杨-米尔斯场理论并非万能，它在解决实际问题的过程中有无法解释的问题，这就引出了上帝粒子的理论。在后面我们将继续讨论如何统合几种基本作用力的问题。直到上帝粒子，也就是希格斯理论以及标准模型的提出，粒子物理才真正在一定程度上达到了统合。
第四节 杨-米尔斯场理论的未解之谜
质量问题
杨-米尔斯场理论用规范对称性、规范场的思想全面解释了基本粒子之间是如何相互作用的，它刷新了我们对于基本粒子的认知。我们通常从粒子具有的性质（如色荷、味荷、电荷）出发认知基本粒子，但是如果不讨论这些荷的相互作用，只讨论它们本身是没有意义的，因为它们只是个名字而已，甚至如果没有这些相互作用的话，我们根本意识不到它们的存在，因为我们感知到它们的存在本质上是我们能与它们发生相互作用，相互作用才是更本质的。
在规范场论之前，我们实际是用了反向的逻辑顺序去认知这些基本粒子。正确的顺序应当是：这些不同的荷的波函数对应于不同的规范对称性，不同的规范对称性揭示了必然存在不同的规范场。这些荷的本质是在不同的规范场中激发起不同的规范玻色子，规范玻色子在色荷、味荷、电荷中相互交换，从而产生力的效果。我们通过对作用力的认知，认知了几种荷的存在并反向定义了色荷、味荷、电荷。
这里面的核心理论，就是杨-米尔斯场，也就是规范场论的思想。是杨-米尔斯场用局域规范对称性将这一系列的性质联系在了一起。虽然杨-米尔斯场的思想是正确的，但是它在实际应用中遇到了问题。
比如通过三种规范场，我们可以解出三类用以交换的粒子，从而产生三种作用力。杨-米尔斯场精确预言了这三种粒子的性质，但有一件事情单用杨-米尔斯理论解释不了。通过杨-米尔斯场的计算，这三类用以交换的粒子的质量都应当是0，它们的运行速度都应当是光速。不过，根据实验的测量，虽然光子和胶子质量确实是0，运动速度为光速，但是W+、W-和Z0这三种负责弱相互作用的规范玻色子质量不为0。这跟杨-米尔斯理论的描述是不相符的，也就是杨-米尔斯场理论无法解释弱相互作用的三种规范玻色子的质量是怎么来的。
最小作用量原理（principle of least action）
为了解决这个问题，要先介绍一下量子场论的基本研究方法。它对应一条原理——最小作用量原理。
为了讲明白最小作用量原理，我们还得把时间倒回到牛顿时代。牛顿定律描述了力学系统的运动状态，原则上只要解牛顿方程，多复杂的经典力学系统都可以解出来。但是有比牛顿力学更为具有统合性的方法，那就是拉格朗日（Joseph-Louis Lagrange）和哈密顿（William Rowan Hamilton）的理论力学体系。
首先，对于一个系统，我们可以定义一个量，叫作拉格朗日量（Lagrangian），用字母L表示。一个力学系统的拉格朗日量可以简单地理解为它的动能减去它的势能。我们假设系统有一个初始状态，以及一个最终状态，作用量（action）就定义为系统的拉格朗日量在初始状态到最终状态这两个状态之间时空路径的积分。也就是把这条路径上每个点的拉格朗日量加起来，用字母S表示。
最小作用量原理可以表述为：一个系统的运动轨迹，就是那条让作用量S最小的轨迹。这就是理论力学对于牛顿力学的统合。这套最小作用量原理放在任何系统，哪怕是量子系统也适用（在量子场论中，最小作用量原理表述在费曼的“路径积分”中，本书不对路径积分的思想作单独讲解，建议感兴趣的读者可自行研究）。把量子系统的动能减去势能，在时空维度上做积分，得到作用量S。再将S最小化，就能得到量子系统运行的规律。最小作用量原理像是能量最低原理的推广。
从计算角度来看，要求解量子场的问题，本质上是要找出不同量子场正确的拉格朗日量，但是对于复杂的量子系统，拉格朗日量不是那么好写出来的。除了实验能测量到的一些数值以外，我们不知道有哪些东西还对拉格朗日量有贡献。
杨-米尔斯场的研究方法，本质上是让量子场的拉格朗日量满足局域规范对称性。所以，拉格朗日量的形式中，必须包含一个新的规范场，这才推出了不同规范场的存在。规范场里激发起来的就是交换用的规范玻色子，它对应于不同种类的力。但是在杨-米尔斯场的拉格朗日量里，并没有规范玻色子质量的踪影。
也就是在杨-米尔斯场的拉格朗日量里，并不存在规范玻色子的质量。根据杨-米尔斯场的计算，规范玻色子的质量必须为0。所以在杨-米尔斯场方程中，被激发起来的粒子都应该是0质量、以光速运动的粒子，这对于强力和电磁力来说是对的。但是对于传播弱力的W-、W+和Z0这三种粒子，它们通过实验测量出来是有质量的，这就没法用杨-米尔斯场解释了。因为它们的拉格朗日量里，压根儿就没有质量。
自发对称性破缺（spontaneoussymmetry breaking）
这个问题的解决是非常曲折的，最初，一个叫南部阳一郎的日本物理学家提出了一个非常神奇的概念，叫作自发对称性破缺。
根据之前说的，这些量子场的拉格朗日量里根本就没有质量。如果有质量，这些拉格朗日量在数学形式上就无法满足局域规范对称性了。杨-米尔斯场理论的核心，是因为满足了局域规范对称性，所以存在规范场。规范场的激发，给出了用来交换的粒子。如果杨-米尔斯场理论是正确的，这些量子场的拉格朗日量就必须要满足规范对称性。如果要满足对称性，这些规范玻色子就不能有质量。如果有质量，就破坏了规范对称性，那么杨-米尔斯理论的根基就不稳了。
要么杨-米尔斯理论是错误的，要么这些规范玻色子不能有质量。但是实验测出来的弱相互作用的三种玻色子确实是有质量的，也就是说，质量的存在与局域规范对称性从根本上是矛盾的，二者只能选其一。
自发对称性破缺本质上就是去融合这两个看似矛盾的条件，做到有质量的同时不破坏规范对称性的。自发对称性破缺讲的是对称性确实没了，也就是质量其实就体现为对称性的破缺和丢失，并且这个破缺的过程是“自发”的。我们接下来解释什么是“自发”。
系统实际的运行方式是让作用量最小的运行方式。那么，有没有可能系统的拉格朗日量满足规范对称性，但在实际的运行过程中表现为破坏对称性的方式呢？描述系统的拉格朗日量是个方程，这个方程确实是满足规范对称性的。但真实的运行方式是要去解这个方程，如果这个方程的解不满足规范对称性，也就是真实的运动方式不满足规范对称性，这不就与有质量不矛盾了吗？方程对称但解不对称，所以真实的运动方式表现为有质量。而实验去测量的是真实的运动方式，不是方程。
这就好比，一桌人围着圆桌吃饭，每两个人中间都放了一副碗筷。由于是个圆桌，所以每个人左边和右边都各有一副碗筷，这样安排，碗筷的数量和客人的数量是相等的，每个人都可以有一副碗筷。在吃饭前，整个系统是非常对称的。这就像在真实运行前，整个系统的方程是非常对称的。但是开始吃饭的时候，由于有的人是左撇子，有的人是右撇子，就一定会有人去拿左手边的碗筷，有人去拿右手边的碗筷。所以最终的结果，大概率会有人因为左边的和右边的碗筷都被人拿了而拿不到碗筷，于是这个系统在真实运行时变得不对称了。
这就是自发对称性破缺想要阐明的道理。它给出了一个解决杨-米尔斯理论问题的办法，让杨-米尔斯场的方程保持对称性。但是真实的运行轨迹却破坏了对称性，导致质量的产生。这里的自发说的就是这种对称性的破坏并非体现在方程里，而是体现在真实的运行方式当中，它不是人为设置的。自发对称性破缺机制以及上帝粒子的提出，切实解决了弱相互作用中规范玻色子存在质量的问题。
第五节 标准模型与上帝粒子
本节继续深入讨论杨-米尔斯理论中遇到的质量问题是怎么解决的。南部阳一郎提出了自发对称性破缺机制所引出的希格斯理论，彻底解决了这个问题。
最小作用量原理
还是要先回顾一下杨-米尔斯理论的方法论。我们要尝试写出这些量子场的拉格朗日量。根据杨-米尔斯理论，这些拉格朗日量应当要满足局域规范对称性。根据局域规范对称性，可以得出存在各种各样的规范场。不同的规范场其实就是不同的荷提供的场，比方，电荷满足的U（1）规范对称性，可以推导出必然存在一个U（1）规范场。这个规范场就是电磁场。根据规范对称性，我们得到了一个比较正确的拉格朗日量。有了拉格朗日量，就可以定义另外一个量，叫作用量。这个作用量就是将在不同时空位点的拉格朗日量做积分加起来。有了作用量，我们就可以去求解系统的真实运动方式。这个真实的运动方式，对应于让作用量最小的那些运动方式。
自发对称性破缺认为这个作用量的方程固然满足规范对称性，但是那个真实的、让作用量最小的运动方式，也就是这个方程的解的对称性是破缺的。
希格斯玻色子（Higgs boson）：质量的成因
有了自发对称性破缺的机制，就能解决质量问题了。在1962年、1963年，三个小组，六位物理学家，几乎同时提出了解决质量问题的机制——著名的希格斯机制（Higgsmechanism）。
希格斯机制说的是：存在一种弥漫全空间的量子场，叫希格斯场。弱相互作用的规范场会与希格斯场发生相互作用。作用的过程中，有自发对称性破缺机制，破缺以后就导致W+、W-、Z0三种玻色子获得了质量。弱相互作用的规范玻色子本身是没有质量的，并且从弱相互作用的本质上来说，它的强度应该当是比电磁力还要强一些，但是由于它们会与希格斯场进行相互作用，这种相互作用会产生一个新的拉格朗日量。这个新的拉格朗日量的解，是会发生自发对称性破缺的，破缺了之后就体现为有质量了，并且由于获得了质量，等效的弱相互作用力就变得极弱了。这个物理过程可以如此定性理解：强力、电磁力交换用的胶子和光子都是静质量为零、以光速传播的，因此强力和电磁力交换粒子的效率高，导致强力和电磁力的强度强；弱相互作用交换的W+、W-和Z0玻色子有质量，所以体现为交换效率低，从而导致弱力的强度弱。
质量这个性质，通过希格斯机理有了全新的解释。粒子的质量，其实体现为与希格斯场的相互作用。如果一个粒子不与希格斯场相互作用，则体现为没有质量，运动速度为光速。比如光子没有质量，运动速度就是光速。
粒子只要与希格斯场有相互作用，就体现为有质量。粒子与希格斯场相互作用的效果，其实是希格斯场对于粒子运动的阻碍。这种与希格斯场的相互作用，体现为希格斯场与相应的粒子作用后发生的自发对称性破缺。
希格斯场是一种量子场，它也像一盆肥皂水。希格斯场被激发起来的粒子叫希格斯粒子，也叫上帝粒子。它是万事万物质量的成因，没有质量，就没有引力，没有引力，天体就无法形成，更不会有恒星、行星、地球，甚至生命。正因为希格斯粒子提供了质量，才能让我们的宏观世界存在，这就像西方宗教体系里说的“上帝创造世界”一样，所以希格斯粒子也被称为上帝粒子。
希格斯机理在1964年就被提出了，但是到2012年才被证实。因为要在实验中探测到希格斯粒子，需要非常高的能量等级。瑞士的大型强子对撞机建成才能做如此高能量等级的实验来证实希格斯粒子的存在。希格斯等物理学家也于2013 年获得了诺贝尔物理学奖。
标准模型
随着希格斯粒子被证实，20世纪的粒子物理学基本封顶。希格斯粒子，以及之前所有关于基本粒子的研究，被统合成了一个相对终极的理论，叫作标准模型。研究出标准模型的物理学家主要有三位，分别是温伯格（Steven Weinberg）、格拉肖（Sheldon Lee Glashow）和萨拉姆（Abddussalam），他们于1979年获得诺贝尔物理学奖。
标准模型的核心信息是什么呢？标准模型做的事情，其实是以杨-米尔斯理论为根基，把实验室里能够探测到的所有基本粒子做了一个集中的描述，这个描述是这样的：
第一，标准模型不讨论引力，只讨论强相互作用、弱相互作用和电磁相互作用。
第二，色荷参与强相互作用，味荷参与弱相互作用，电荷参与电磁相互作用。
第三，夸克是参与所有4种相互作用的基本粒子，总共有36种。36种夸克对应于3种色荷与6种味荷，分别是红、绿、蓝三色和上夸克、下夸克、奇异夸克、粲夸克、顶夸克、底夸克。它们都是费米子，都有各自的反粒子。
第四，电子、μ粒子和τ粒子参与除强相互作用以外的其他三种相互作用，电子中微子、μ中微子和τ中微子，这三种中微子则只参与弱相互作用和引力相互作用（也有理论预言中微子也许极其微弱地参与电磁相互作用，但实验上并无此实证）。
第五，三种相互作用是靠不同的荷之间交换规范玻色子实现的。强相互作用是一种力，由色荷之间交换胶子实现。胶子也携带色荷，一共有8种。之所以是8种，是因为色荷有3种，排列组合形成的量子叠加态有8种，对应8种胶子。弱相互作用也是一种力，由味荷之间交换 W+、W-、Z0三种规范玻色子实现。电磁相互作用同样是一种力，由电荷之间交换光子实现。
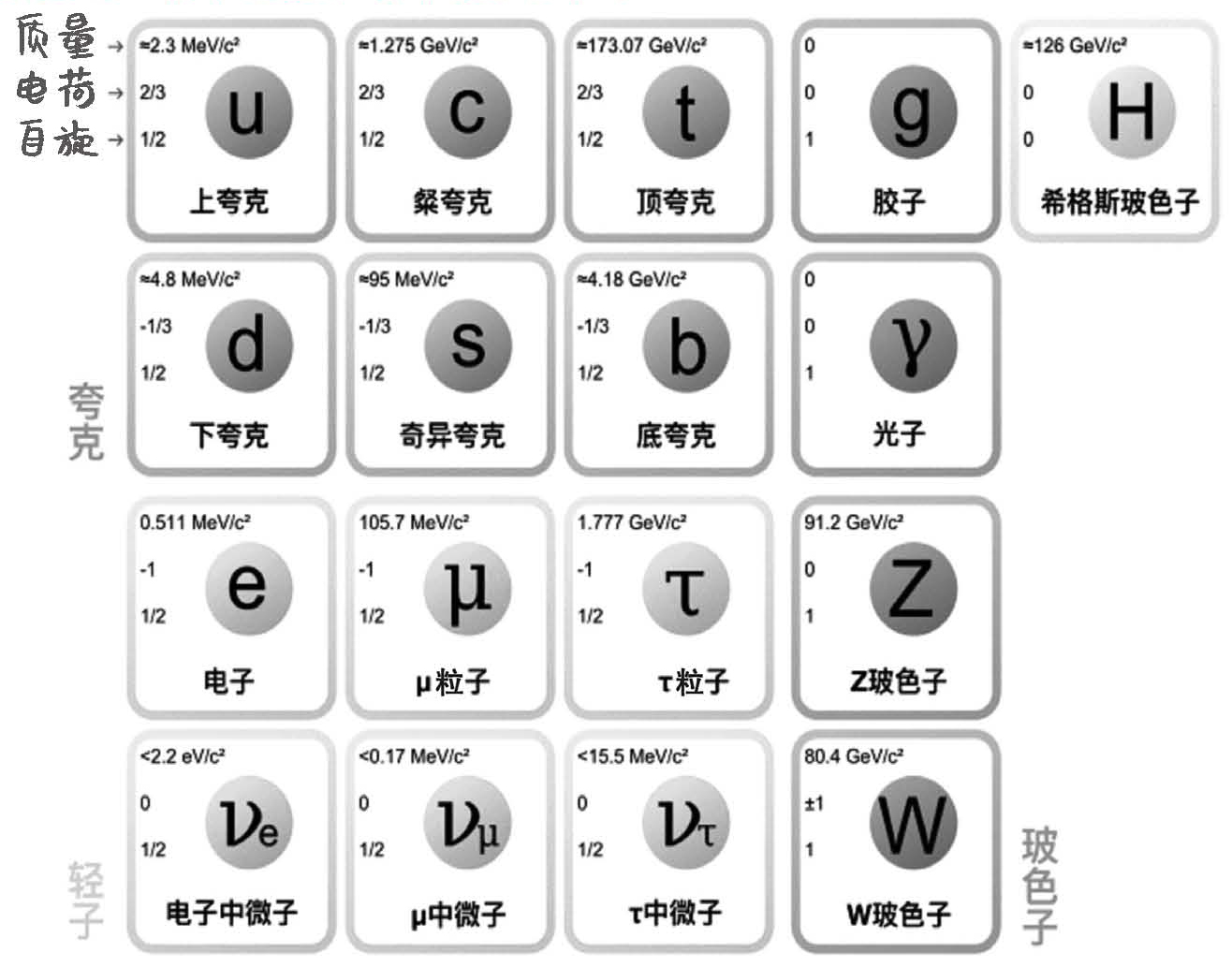
图14-5 标准模型中的所有基本粒子
第六，胶子是因为色荷的波函数满足SU（3）对称性，因此胶子本质是由SU（3）规范场激发出来的，胶子没有质量。光子是因为电荷的波函数满足U（1）对称性，因此光子本质上是由U（1）规范场也就是电磁场激发出来的，光子也没有质量。W+、W-、Z0三种规范玻色子是因为味荷满足SU（2）对称性，因此这三种玻色子是由SU（2）规范场激发出来的。这三种玻色子有质量，是因为它们与希格斯场相互作用经历了自发对称性破缺。
第七，存在一种弥漫全空间的场，叫希格斯场。希格斯场激发出来的粒子叫希格斯粒子，是一种玻色子，它是质量的成因，其他基本粒子有质量是因为与希格斯场发生了相互作用。
标准模型一共描述了以下61种基本粒子。
夸克有6种味，分别是上、下、奇、粲、顶、底，并且每种夸克都可以有三种色——红、绿、蓝，于是夸克有18种。对应地，夸克都有反夸克，所以夸克和反夸克总数是36种。
轻子有6种，算上它们的反粒子，总共有12种。
胶子有8种，它们的反粒子就是自己，W-和W+互为反粒子，Z0自己是自己的反粒子，算上光子，光子也是自己的反粒子。规范玻色子一共有12种。
再加上希格斯玻色子，总共有36+12+12+1=61种基本粒子。
标准模型无法解释的问题
标准模型可以说是20世纪粒子物理学极其成功的理论模型，因为它与实验的结果符合得非常好。但是标准模型还有不少没有解决的问题，甚至可以说，标准模型几乎一定是一个暂时性的理论。
标准模型解释了四种相互作用当中的三种，用杨-米尔斯场和希格斯场，描述了三种相互作用，把它们统一在同一个理论框架内。但我们知道，强力比电磁力强得多，电磁力又比弱力强得多。虽然标准模型没有解释引力，引力又比弱力弱得多。为什么这四种相互作用的强度会差那么多？这是标准模型没有从原理上回答的。
标准模型把这几个力的强度当成既定事实。我们知道，引力的强度是用万有引力常数来表征的。万有引力常数G非常小，数值上为6.67×10-11。电磁力的强度，用库仑常数表征，数值上为9×109，非常大。在标准模型里，表征强相互作用、弱相互作用和电磁相互作用的作用常数，是三个不同的数值。这三个不同的数值，是依靠实验测量出来的，并非通过标准模型经过演绎法推导出来的。也就是说，标准模型无法解释为什么这几个作用常数差别那么大。真正意义上对于几种力的统一，应当在表达式中只有一些最基本的常数是靠实验测量的，其他的东西都应该由演绎得来。而标准模型当中需要实验测量的参数太多了，有30多个。因此，标准模型一定是一个不够基本、不够终极的理论。
除此之外，标准模型依然没有办法解决我们最初的问题：存不存在德谟克利特意义上的原子？标准模型里的基本粒子还有很多：36种夸克、12种轻子、12种规范玻色子、希格斯粒子。也就是说，标准模型远远还不能回答我们最初的问题：什么是终极的、单一的、万事万物的基本构成？
虽然有很多问题无法回答，但在我们目前能够做实验的层面上，标准模型已经是最先进的理论了。再去探索，必须让实验水平跟上。也只是在2012年，我们才验证了希格斯粒子。如果要继续去追求终极，恐怕短时间内实验水平是跟不上的，但是科学家在这条道路上还是有非常多的理论性尝试的，它们指向终极的理论。比如大统一理论、超对称理论和弦论，这些理论都是对终极问题的探索。但是目前没有一个理论得到了任何实验证据，且指向终极。还不止这些，正是因为没有实验的论证，才导致可能的理论非常多。对于终极理论的探索，科学家们还有很长一段路要走。