材料物理
第一节 材料的力学属性
物质的常见形态有三种:固态、液态、气态。其中,气态在“极热篇”已经通过理想气体模型等物理学模型讨论过了;对于液态,我们更加关心的是它的流体力学特性;物质的固态则是“极冷篇”要关注的对象,我们将从宏观到微观一层层地讨论下去。
固体的性质各异,物质种类上就有金属、准金属、非金属等许多固体物质,微观结构上也有晶体、非晶体之分。本章先讨论固体较为宏观的性质,分别是力学性质、热学性质、电学性质和磁学性质。
应力和应变
之前在“极快篇”第二章简单提过应力、应变,在这里,我们先聚焦在材料众多性质中最宏观的力学性质上。假设现在有一块固体,我们可以通过各种手段对它的属性进行测试,其中最宏观、最容易操作的就是它的力学属性。
假设有一块金属,我们可以尝试去拉伸、压缩、扭曲它,给它施加不同大小以及方向的力和力矩,则金属会在不同情况下发生不同方式的形变。那这块金属在外力作用下的形变规律是什么样的?再极端一些,我们要用多大的力或者力矩,才能把这块金属拉断、压坏、扭断?
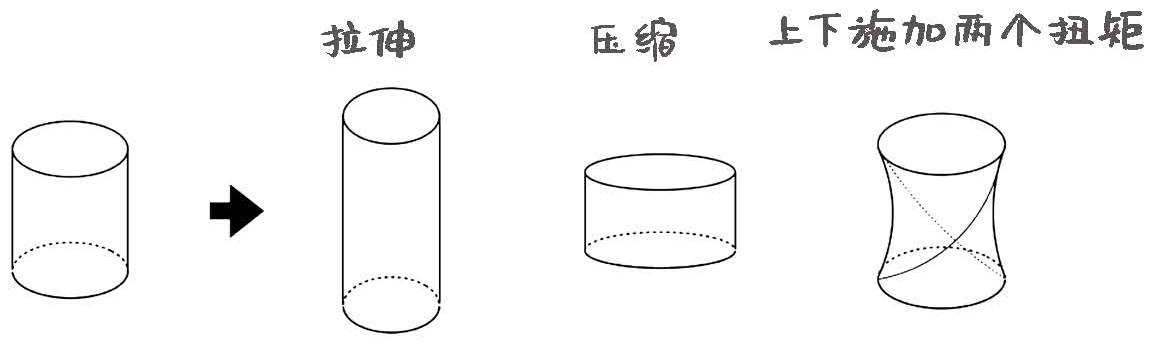
图18-1 对圆柱体施加应力
假设现在有一块圆柱形金属,我们可以在两端施加两个圆柱体轴向的力去拉伸它,也可以反过来压缩它,这两个力垂直于两个圆柱的底面。拉伸的力会让圆柱体变长,压缩的力则会让它变短。如果施加垂直于轴向的力,则会让圆柱体变歪。如果上下施加两个方向相反的扭矩,圆柱体会被扭曲。
应力,就是在固体某处单位面积上施加的力,它是一个矢量,既有大小,也有方向。除了应力之外,还有应变。应变,被定义为物体形变之后的长度减去原长度的差值与原长度的比,应变其实就是物体形变的百分比。
张量
有了应变和应力的定义,我们最关心的是它们之间的关系,也就是施加一定大小和方向的力之后,固体的形状会发生什么变化。比如我们都很熟悉的弹簧,在对其施加一定的拉力或者压力后,它都会发生形变,拉伸会变长,压缩就会变短。我们关心的是弹簧的长度如何随着施加压力或拉力大小的变化而变化,这里就有了著名的胡克定律(Hooke's law)。
胡克定律说的是,弹簧变化的长度正比于弹簧受到的力。用公式表示就是F=-kx,其中,F是外力,x是弹簧的形变,k是弹性系数,这里的负号表示弹簧的弹力方向永远与位移的方向相反,也就是弹簧弹力的趋势永远阻止位移变大。比如,拉伸弹簧时,弹簧的拉力趋势会阻止拉伸;如果压缩弹簧,弹簧的弹力趋势则会阻止压缩。
但是对于一块固体,应力和应变的关系就没有那么简单了。微观层面上,我们可以把固体想象成是由分子或原子相互聚集、连接组成的,分子和分子、原子和原子之间相当于用很多弹簧连在一起。固体里的弹簧是三维的弹簧,因为各个方向都有作用力的产生。但是满足胡克定律的弹簧是一维的,它的形式很简单,因为我们只考虑它向一个方向压缩或者拉伸变形。对于一个固体,每个分子、原子都与多个相邻的分子或者原子相连,每一个连接都可以当成一个弹簧,这里的情况是极其复杂的。
这里就出现了一个类似于胡克定律中弹性系数k的量。胡克定律中的k只不过是一个数字,但是固体的弹性系数是一个张量,它的数学形式不是一个数值,而是一个矩阵,有好多个数值。
什么意思呢?我们来看一下几种简单的情况。
从两端拉伸一个圆柱形的固体,它除了变长以外,还会变细。可以建一个直角坐标系来描述这种行为,假设圆柱体中轴的方向与坐标系z轴的方向平行,圆柱体的横截面则在坐标系的x、y方向上。也就是说,施加了z方向的应力之后,除了有z方向对应的应变以外,圆柱体还有x和y方向上的应变。同样地,如果在z方向上压缩,圆柱体除了在z方向上变短以外,在xy平面方向上会变粗。其他的应力也一样,比如扭动圆柱体,圆柱体会变长,腰部会变细。
也就是说,给固体施加一个方向的力,相应的变化不光是一个方向的,而是三个方向都可能有。这种情况下就不能用一个单一的弹性系数来描述应力和应变的关系了,而是一个应力对应于所有方向的应变。这个弹性系数至少有九个分量,分别对应的是三个不同方向的力,每个方向的力都会引起三个方向上的形变,即3×3=9。
上面讨论的是力的方向,但是不要忘了,力有三要素:大小、方向和作用点。对固体来说,力作用在哪里也很重要。把固体中的一个小方块作为研究对象抽象出来看,这个力可以作用在小方块的三个方向上,可以是上下面、左右面或者前后面。三个不同方向的力可以作用在三个不同方向的面上,这样应力就有了九种可能性。
应变也是一个道理,它可以是三个不同面,每个面都有三个不同方向的形变,这样的话,形变也有最多9个量。所以,一共有9个应力对应9个形变,也就是任意一个应力有可能对9种形变方式都存在作用,这样一来,固体应该最多有9×9=81个弹性系数,它对应于9个应力中的每一个,都会对全部9个应变产生作用。

图18-2 应力与应变的关系(各项同性材料性质的弹性方程,由于材料的对称性,通常只会用到6×6的弹性系数张量,ε和γ都表示应变,σ都表示应力,E是材料的杨氏模量,ν是材料的切向模量)
对于有规则内部结构的固体,这81个系数,不会是81个独立的数值,一个方向的应力并不一定会导致所有方向的应变。比如上下拉伸一块匀质的橡皮圆柱体,它只会变长、变细,但不会发生扭动。因此,拉力对应于扭动形变的系数,应该是0,这样81个系数会大大减少,甚至大部分系数是0。
这个以9×9矩阵表现的弹性系数,就是一块固体的弹性系数张量。但是实际情况下,我们不会用到9×9的弹性系数张量,通常由于材料的对称性,6×6的弹性系数张量就足够了。应力和应变也因为有一定对称性,并不需要9个相互独立的应力和应变,而是6个相互独立的应力和应变足矣。
这也是为什么力学虽然古老,但是机械工程、固体力学到今天依然蓬勃发展,一个重要原因就是这里面的计算太复杂,情况太多变。
振动模式(vibrationmode)
有了张量的定义,就可以充分研究固体的性质了。其中,固体的振动模式是我们非常感兴趣的。一个弹簧上面连着一个小球,把弹簧拉开再放手,小球就会开始振动且频率固定,这个振动频率就叫弹簧小球系统的振动模式。
固体也一样,有了固体的弹性张量,我们就可以计算固体有哪些振动模式。这就对应了各式各样的机械波在固体里是如何传播的。这种研究方式非常有用,在各个领域都可以说是一种基本思想。比如研究地球的结构,尽管人类无法下到地幔、地核,但可以把地球抽象成为一个弹性体,通过分析地震波的传播情况,可以得出地球的地核是一个固体金属球的结论。
强度与硬度
我们刚才讨论的都是固体的弹性形变(elastic deformation),那什么叫弹性形变呢?就是指这个应力的作用范围并不大,放开应力之后,固体还能恢复到原来的形状。但是这种弹性形变有一个极限,如果应力过大,导致形变过大,超过极限后,固体就无法恢复到原来的形状了,这种情况叫塑性形变(plastic deformation),这就完全属于固体另一个范畴的力学性质了。比如,固体有强度的定义,当施加超过固体能承受强度极限的应力,固体就会断裂。硬度的定义和强度有些类似,只是强度是整体性质,硬度是局部性质,固体材料能够承受的最大的局部压力就表明了它的硬度。
第二节 材料的热学属性
当我们面对固体的时候,最容易想到的就是材料的力学属性,从实验测试操作的难易程度来说,力学属性的测试也是最直接的。比力学属性稍微复杂一些的是固体的热学属性,也就是固体跟温度的关系是什么样的。
总的来说,我们关心的固体热学属性有三个:比热(heat capacity)、热膨胀系数(coefficient of thermal expansion)以及热传导性(heat conductivity)。
比热
比热(也叫比热容)的概念我们初中的时候就学习过,它是指让单位质量的物质上升单位温度所需要的能量。水的比热是比较大的,让1kg水上升1℃,需要4200焦耳的能量,但是让1kg铁上升1℃,大概只要水的1/10能量就够了。
到底是什么导致了不同物质的比热不一样呢?
首先要明确固体温度升高的本质是什么。温度正比于微观粒子动能的平均值。任何固体中的微观粒子就是指组成它的分子、原子。温度的上升无非就是这些分子、原子的运动速度的增加。除此之外,很多材料(尤其是金属)中有大量自由电子,温度上升,也包含了电子的自由运动变得更剧烈的物理过程。
固体中原子和分子的位置相对固定,所以对于固体,温度的升高代表它的分子和原子在固定位置周围做振动的剧烈程度增加。
不同固体的比热不一样,输入的能量在分子、原子的动能和势能中如何分配。一份能量输入后,比热大的物体分配给分子之间作用势能的部分较多,那么根据能量守恒,它分配给分子动能的部分就较少。
拿陶瓷和金属做一个简单的比较,陶瓷的比热比金属更大,本质是陶瓷分子之间的作用比金属更强。上一节我们说过,这些固体的分子之间就像有“弹簧”连接一样。通过宏观性质可以知道,陶瓷的“弹簧”显然比金属的“弹簧”更紧,陶瓷比金属硬,陶瓷是脆的,而金属相对较软,容易变形。既然陶瓷材料的分子之间的绑定更紧,那么紧的“弹簧”对于同样幅度的振动,它所储备的弹性势能更大。所以,对于硬度大的材料,一份能量输入,肯定会更多地分配给分子间的势能,少量分给动能,而固体的温度只表现为这种分子的动能。所以同一份能量输入,较硬材料升温的程度肯定较小。
除此之外,像金属这样的材料,由于内部有大量的自由电子(自由电子的势能接近于0,否则不会那么自由,如果给自由电子输入一份能量,几乎都会用来转化为电子的动能),所以它的升温效果明显,所以比热较小。
比热并非一成不变,不同温度情况下,分子、原子之间连接的弹簧的弹性系数会发生变化,同样,比热也会随温度,甚至固体所处环境的外部压强而变化。
热膨胀系数
除了比热,固体的热膨胀系数也是我们关心的物理量,它用来定量描述热胀冷缩现象,并告诉我们不同的固体在加热的情况下,具体会膨胀多少。
热膨胀系数为什么这么重要呢?因为在实际的工程中,材料的热胀冷缩是必须要考虑的。比如,传统火车轨道的每一段钢轨并非完全严丝合缝地拼接,而是要留出一段距离,就是考虑到不同季节钢轨的热胀冷缩;家里地板的铺设,在每块木板之间留有一定的缝隙,也是考虑到木头的热胀冷缩。
乍一看,热胀冷缩现象的发生是因为温度的升高,分子和原子振动更加剧烈,振动幅度更大,导致物质的总体效果呈现为体积更大。但这种判断是错误的,固体会热胀冷缩的根本原因,不是分子之间的振动更加剧烈,而是分子势能的非对称性。
分子之间存在范德瓦耳斯力,这是一种非对称的力,靠得近的时候表现为排斥,离得远的时候表现为吸引,这种特性跟弹簧一样,它总有把你拽回或者推回它平衡位置的趋势。但是弹簧的拉伸和压缩所提供的弹性力是对称的,也就是说,压缩和拉伸1 cm,感受到力的方向虽然不同,但大小一样。可以想象弹簧上连着一个分子,加热分子让它振动起来,由于弹力是对称的,拉伸和压缩的难度相同,所以分子在拉伸和压缩下的振幅相同,平均下来分子振动的整体平均幅度没有变化,平均的平衡位置不发生变化。
从图18-3中可以看出,范德瓦耳斯力这根“弹簧”是非对称的,在压缩和拉伸长度相同的情况下,获得的压缩推力比拉伸拉力要大。换句话说,就是比起压缩,拉伸范德瓦耳斯力这根“弹簧”更容易,也就是升温的时候,同样一份分子振动动能,拉伸的距离更多,压缩的距离更少,平均下来分子振动的平均振幅不在原来的平衡位置,而是偏向于拉伸的那一侧,这才是物体热胀冷缩的根本原因。换句话说,如果分子势能完全对称,则不会存在热胀冷缩的现象,不同温度下体积不变。
图18-3 范德瓦耳斯力:在平衡位置附近的弹力和拉力并非对称
我们可以用热膨胀系数来描述热胀冷缩的现象,提升单位温度,体积增加的百分比就是热膨胀系数。
热传导性
除此之外,我们还关注热传导属性。根据生活经验,金属传热比陶瓷传热更快,所以烧水要用铁壶,泡茶要用瓷壶,就是因为金属的导热性比陶瓷的导热性好。
导热性由什么决定呢?这其实跟比热高度相关。通常,比热小的固体的导热性比比热大的固体好。因为比热小的固体,大部分的能量摄入被转化成了分子、原子的动能,而导热的本质就是分子间动能的传递。
固体中热传导的过程通常分为两部分:一部分是固体的分子和原子振动的传导,对于晶体,则是晶格的振动;另一部分是由自由电子携带动能的传导。导热性好说明热量的传递效率高。
热应力(thermalstress)
了解了固体的比热、热膨胀系数和导热性之后,在实际应用中,我们还会关心固体的热应力,也就是指当固体受热之后产生局部的热胀冷缩效果,这种局部的热胀冷缩未必是均匀的,从而导致局部的形变产生局部的应力。
在工程结构中,不同固体以一定的方式进行连接,比如汽车发动机中气缸、活塞等部件会在温度变化极其剧烈的环境下工作,它们的空间位置是有固定关系的。但随着温度的变化,部件之间的作用力也会相应发生变化,要保证工程结构继续运转,热应力就是需要充分考虑的因素。
现实工程问题中,物体的受热变化有可能会非常不均匀,比如一个部件的不同位置受热是不一样的,这会在它内部形成热应力。此外,部件还会有忽热忽冷的情况,我们都知道,一个冷的玻璃杯如果突然倒入开水会碎裂,这就是热应力的表现。材料热应力研究在工程中是极其重要的。
第三节 材料的电学属性
了解了固体材料的力学性质和热学性质之后,我们还能直接测试材料的电学属性。
导体(conductor)和绝缘体(insulator)
定义绝缘体或导体,取决于这种材料是否导电。比如金属一定是导电的,且不同金属导电性强弱不同。铜的导电性最好,铝次之,银再次之。陶瓷是不导电的,塑料也不导电。
导电性的本质是什么呢?
先来讨论什么叫导电。所谓导电,就是固体材料中可以形成电流。电流就是带电粒子的定向运动。要想让一个线圈里产生电流,就要接电池使线圈的两端产生电压。电压的本质是在导线里建立一个电场让带电粒子感受到库仑力。在库仑力的推动下,带电粒子就开始了定向运动,这种定向运动就是电流。
导体和绝缘体最大的区别就是导体中存在大量的自由电子,这些电子几乎不受原子核的束缚,可以在导体内部自由运动,温度越高,电子运动的速度越快。这些运动是无规律的,各个方向都有,所以宏观上没有形成整体的定向运动,不体现为电流。
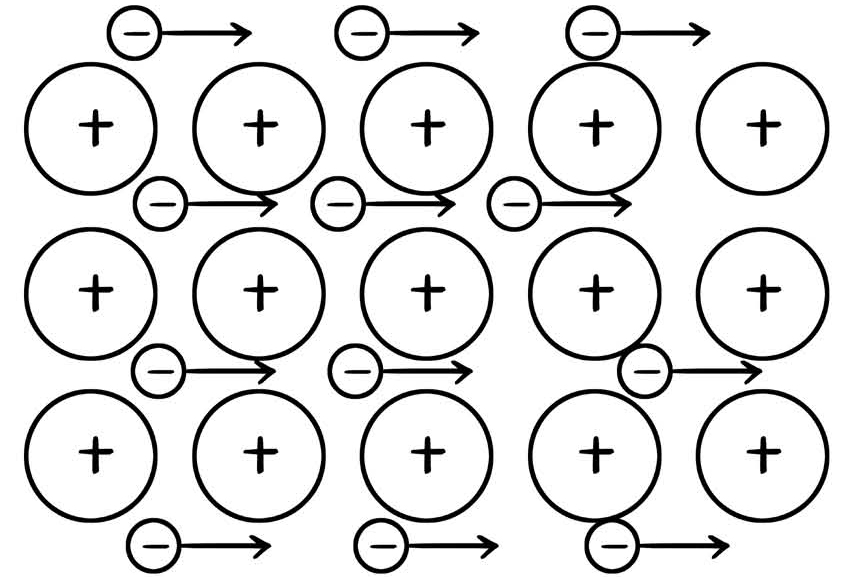
图18-4 导体中电子的定向移动
但是加了一个电场以后,这些电子就在保持原有无规律运动的情况下,又加上了一个整体运动的趋势,这种整体的定向运动就形成了电流。材料的导电性与导热性的强弱几乎是正相关,导电性强的物质导热性通常也很强,因为导电性强的物质拥有大量自由电子,自由电子的定向运动体现为电流,无规则运动则体现为热量。
绝缘体中没有太多自由电子,绝缘体中,电子大多被束缚在原子核周围,即便加了电场,它们还是无法发生定向运动,因此体现为绝缘。我们在“极热篇”的第十六章曾经说过一种现象叫击穿,在电场足够强大的情况下有可能把绝缘体击穿为导体,比如闪电,就是将空气击穿。
为什么金属中会有很多自由电子,但是绝缘体中就没有什么自由电子呢?这跟不同物质的原子结构有关。我们在“极小篇”曾经讨论过,原子内部的电子是依据薛定谔方程、能量最低原理,以及泡利不相容原理从内到外分层排布的。最外层的电子离原子核远,对于外层电子来说,内层电子的负电荷等效地抵消了一部分原子核的正电荷,所以最外层电子感受到的电磁力比较弱,容易成为自由电子。
原子最外层电子排布的不同,导致了绝缘体和导体在导电性上的差异。原子里电子的排布是根据能量的高低分层的,每一级能量对应于一层电子。根据泡利不相容原理,电子是费米子,每一层能放的电子数有限,具体能放多少取决于每一层的薛定谔方程能解出来多少个能量相同的轨道。
导体和绝缘体的最大区别,就是导体的原子最外层的电子数是少于半数填满的(less than half-filled)。比如,钠原子的最外层只有1个电子,但它的原子最外层最多可以放8个电子;同样是最外层可以放8个电子的氧,其原子最外层有6个电子,是多于半数填满的(more than half-filled)。金属之所以呈现为金属,恰恰是因为它的原子最外层电子数少于半数填满。氧这样的绝缘物质,其原子最外层电子是多于半数填满的。
原子最外层电子的排布,决定了是否存在自由电子。为什么半数填满如此关键?不如我们来考虑一下原子最外层电子是否自由的问题。对于少于半数填满的电子,要自由运动是非常方便的,因为隔壁的其他原子的最外层轨道非常空,它可以随便去。就像一座公寓里,每家每户都是200m2,每户就住了一个人,想必这些户主串门是非常容易的,因为每个人家里空间都很大,并且自己家人少,比较寂寞,串串门想必是比较开心的。
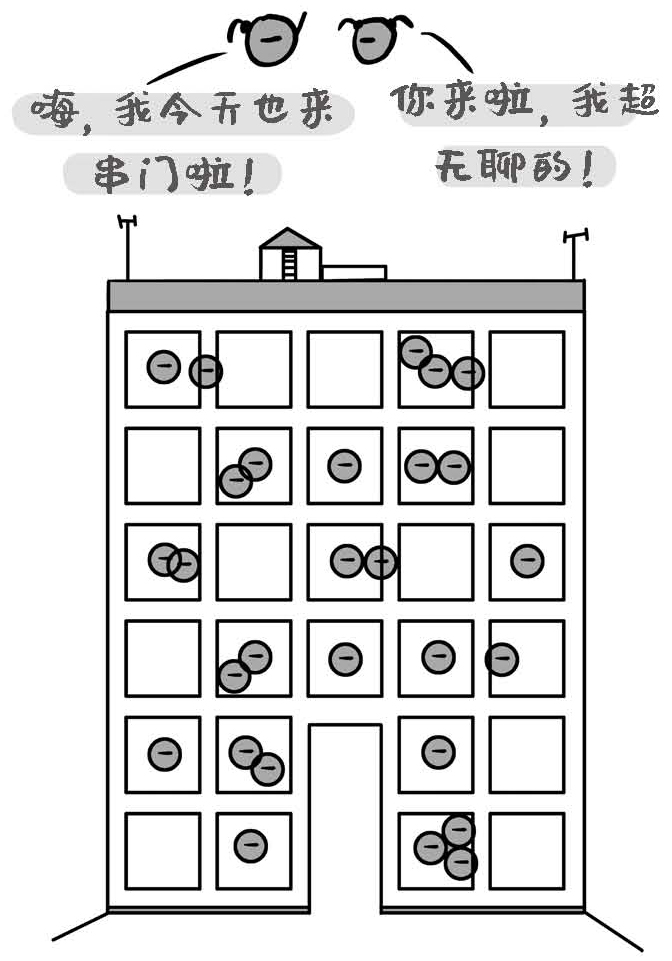
图18-5 原子最外层电子可以自由“串门”
但是,对于多于半数填满的绝缘体来说就不是这样了。比如,氧原子的6个最外层电子出去运动的倾向是一样的,都要出去的话,隔壁的原子是装不下的,因为空间本来就很拥挤了。这就好像一座公寓,每户也就30m2,且每户住了6个人,这种情况下,串门对大家来说都不方便,所以干脆还是别动了。
这就是导体和绝缘体为什么导电性差别很大,导体的原子最外层电子数少,且其他原子最外层的空间多,所以它的电子移动很方便,绝缘体则相反。
半导体(semiconductor)
肯定有一种临界情况,就是原子最外层电子刚好一半被填满,这就得到了半导体,它的导电性介于绝缘体和导体之间。比如硅(silicon),就是一种最理想的半导体材料,它的原子最外层电子数是4个,并且最外层最多能装8个电子,这4个电子是否能去到周围原子的最外层,是相对中立的,所以硅的导电性适中。这种适中的导电性适合用来做成电子电路的逻辑门(logic gate),因此电子电路,尤其是光刻电路,目前都是在硅板上光刻制成。
电阻
衡量材料导电性强弱的物理量,叫电导(conductance)。电导反过来,就是电阻。电阻越大,导电性越差。在被击穿之前,绝缘体的电阻基本可以被认为是无穷大。跟金属有电阻的原理不太一样,绝缘体电阻大的本质是电子被原子束缚住,无法形成电子的定向流动。
但是导体电阻的机制不同。电流在定向运动的过程中,会与原子发生碰撞,由于原子的位置相对固定,且质量是电子质量的几千到几万倍不等,所以原子的存在对于电子来说就像一堵墙。即便原子之间的距离很大,电子与原子的碰撞仍然不可避免,这表现为对电子定向运动的一种阻碍效果。因此导体的电阻大,本质上是因为这种阻碍效果强烈。因为这种碰撞耗散了电子的运动动能,根据能量守恒,最后体现为电子和原子的无规则运动,导致材料温度升高。早年的白炽灯的原理,就是利用电阻产生的热能,提升灯丝的温度,然后通过热辐射的现象发光。
各向异性(anisotropy)
不同导体的电阻大小各不相同,有很多因素影响电阻的大小,例如原子的大小、质量、间距等。晶体还具有各向异性的电阻,因为晶体内部有微观周期性几何结构,电子往不同方向运动,碰撞规律不同,导致了晶体电阻的各向异性。
目前我们只是从宏观上来讨论材料的导电性问题,下一章我们将从量子力学的角度重新审视这个问题。
第四节 材料的磁属性
19世纪英国伟大物理学家麦克斯韦总结出了一切经典电磁现象都满足的麦克斯韦方程组,方程组里深刻揭示了电与磁的关系,电与磁永远相互伴随,变化的电场会产生磁场,变化的磁场也会产生电场。既然讨论了材料的电学性质,势必要讨论材料的磁属性。
不同材料对于磁场的反应不同,比如磁铁只能吸引铁(iron)、钴(cobalt)、镍(nickel),其他金属,如金(gold)、银(silver)、铜(copper)是不会受到磁铁的明显吸引的。再比如有一些材料容易磁化,也就是在磁场里放久了也具有了磁性,有些材料则不容易被磁化。
材料的磁属性,由材料原子中的电子排布规律决定。
什么是材料的磁性?
首先来看看什么性质会让物质呈现跟磁场相关的属性,我们在“极大篇”和“极小篇”都讨论过基本粒子的一种特性,叫自旋。自旋是基本粒子的固有属性,我们可以把这些微观粒子想象成一个个小磁铁,原子中有电子,电子就像一个个小磁铁。不难想象,如果固体材料的性质跟磁有关,那就应该与原子中电子的自旋有关。
每个电子都像是一块小磁铁,但是材料中电子的自旋指向是杂乱的,大多数不是磁铁的材料不会呈现磁性。但是把不同的材料放在磁场中,它们会对磁场有不同的反应,这些不同的反应就是不同材料的磁属性。为什么不同材料会呈现不同的磁属性呢?可以考虑这么一个过程,给你一大把小磁铁,对它们进行排布,排布的方式决定了不同的磁属性。
我们按照原子中电子分层结构来排布电子,依据电子排布方式的不同,不同类型的原子就能获得不同的磁属性。
抗磁性(diamagnetism)
比较常见的磁属性是抗磁性,也就是这种材料如果放在磁场里,材料里的磁场强度会被削弱,这对应的是一种最普遍的电子排布方式。根据薛定谔方程,原子里的电子轨道,是按照能量高低分层的,每层有若干个不同轨道。根据泡利不相容原理,每个轨道可以放两个自旋方向相反的电子,就好比两个反向排列的小磁铁。根据生活经验,我们知道两个磁铁是倾向于反向排列的,同向磁铁的N级和S级之间会互相排斥。
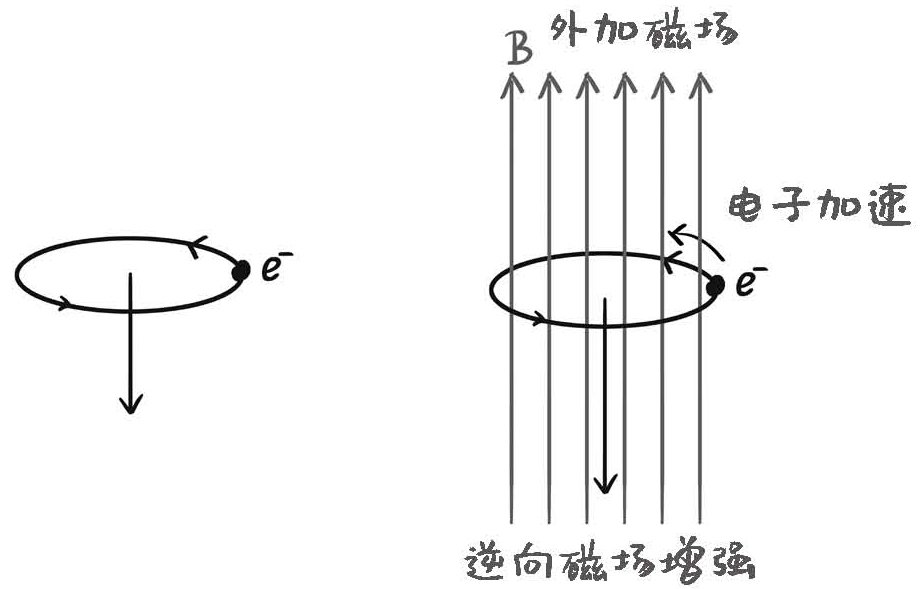
图18-6 在磁场中电子运动受到的洛伦兹力
抗磁性的产生,就是因为一种原子里的电子排布,刚好都是成对出现,每个轨道里都有两个电子,自旋方向相反。这时作用一个磁场在上面,就会削弱磁场。为什么?首先,因为所有轨道都有两个自旋方向相反的电子,所以它们的磁性对外来说是相互抵消的,因此它们不产生净磁场。
但是,这些电子同时还在围绕原子核运动,就好像一股环形电流,它也会产生一个磁场。加上磁场以后,运动的带电粒子会在磁场中受到洛伦兹力的作用,从而改变电子的运动速度。也就是说,原子中的电子运动所产生的环形电流会让原子整体产生一个磁场,环形电流在外磁场的作用下,所产生的磁场与外磁场刚好相反,由此就抵消了一些外部磁场,体现为抗磁性。
顺磁性(paramagnetism)
除了抗磁性,还有顺磁性。顾名思义,就是外加一个磁场,顺磁性材料中的磁场反而要比外加的磁场更强。顺磁性也是由原子内电子排布的特殊规律导致的,比方说一种原子的最外层有5个轨道,并且它也有5个最外层电子,这个时候这5个电子倾向于每个都占据一个单独的轨道,这种规律叫洪德定则(Hund's rule)。
为什么会这样呢?为什么不是每两个电子占据一个轨道,剩下的电子占据一个单独的轨道,然后另外两个轨道空着呢?因为两个电子占据一个轨道,反平行的两个电子,磁的相互作用能量更低。但是5个电子单独排列难道不会增加磁相互作用的能量吗?
这里其实是两种能量的博弈,是磁相互作用能和电相互作用能的博弈。
我们知道,一个稳定系统一定是能量尽量要低。5个电子分开排列,虽然看似磁相互作用能量升高了,但是当5个电子分散在5个轨道当中的时候,对于每个电子来说,原子核的正电荷由于电子的分散会被更少地屏蔽,这样的话每个电子能感受到更多来自原子核的正电荷,与此同时它们离原子核的距离更近,从而降低了电势能。
当5个小磁铁都分占一个轨道时,再加上外磁场,它们都倾向于向一个方向排列,这样5个小磁铁的磁性一致,再加上外磁场,综合起来使材料内部的磁场增强,这就是顺磁体。比如,铝(aluminium)和钛(titanium)就是顺磁体。
铁磁性(ferromagnetism)
像铁这样的物质,如果放在磁铁附近一段时间,就会具备磁性。但是其他材料似乎没有这样的性质,普通的顺磁性材料,把磁场撤掉,材料的磁性也会消失。
因为任何材料都有温度,有温度就代表原子、分子做无规则运动,一旦撤掉磁场,原子的无规则运动就会占据主导地位。因此对于顺磁性材料,如果撤掉磁场,磁性就会随之消失。但是铁却不是这样,虽然铁原子做无规则运动,但是加上了磁场后,即便撤掉,最外层电子同向排列会使得电子电势能降低的程度极高,这就导致铁磁体非常喜欢电子同向排列的状态,因为这可以大大减小它的电势能,总能量也因此降低。
居里温度(Curie temperature)
这就不得不提到一个概念——居里温度,它是法国物理学家居里(Pierre Curie)通过实验发现的一个现象。根据前面的分析,我们发现,材料是否表现出铁磁性,其实是两股力量博弈的结果——到底是热运动想要变乱的趋势更强烈,还是展现出铁磁性时能够获得更低能量的趋势更强烈。
很明显,温度越高,热运动想要变乱的趋势就越强烈,这个温度的临界点就是居里温度,也叫居里点。即便是铁,在加热到一定温度,达到居里点之后,铁磁性也会消失,变成顺磁性。顺磁性和铁磁性的一个本质区别,就是它们所处的温度是在这种材料的居里点以上还是以下。顺磁性物质可以被认为是一种居里温度比较低的物质,室温就已经超过它的居里温度了,铁磁性则相反。
反铁磁性(antiferromagnetism)
抗磁、顺磁、铁磁是三种最为主要的材料磁属性,往下还能根据电子分布规律,划分不同的具体的磁属性。不同种类原子轨道排布的规律都是有差别的,比如反铁磁性,尽管材料当中的电子倾向于规律排列,但它们排列的特点是反平行间隔排列。如果是一个方格结构,第一行是上下上下,第二行是下上下上,也就是说每个电子周围的几个电子跟它都是反平行排列。
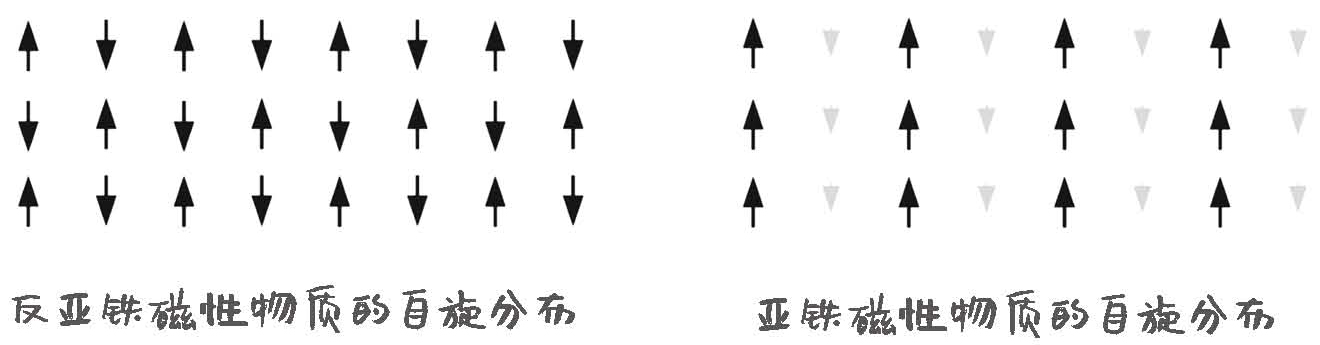
图18-7 反亚铁磁性物质和亚铁磁性物质的自旋分布
如果按照排列规律继续细分,还有亚铁磁性和反亚铁磁性,都与材料的原子排布及内部结构息息相关。
完全抗磁性(super-diamagnetism)
除此之外,超导体具有完全抗磁性,也就是说,磁场完全无法进入处在超导状态的材料,材料内的磁场为0,这叫完全抗磁性。这就是材料的磁属性,总的来说分三种,但是它们最终都可以统一被自旋阵列模型描述。
至此,我们对于材料的各种性质做了比较全面的讨论,但是这种讨论还是比较浅显以及宏观的,最多不过是分析了电子在原子中的排布方式,但是这样的物理学图景太过定性。
真实情况下,材料的微观性质应当运用量子力学的视角进行分析。在真实的固体,尤其是晶体中,电子并非只围绕一个原子的原子核运动,而是呈周期性排列。这种情况下,我们应当研究的是,面对一个周期性排列的原子核系统,电子应当如何运动?它满足的薛定谔方程应该是什么样的?这其实已经进入了固体物理的领域进行探讨,材料的光学性质用固体物理的思想来讨论更加清楚。
