热力学与统计力学
第一节 什么是温度
温度的宏观定义
我们要讨论的“极热”,自然是指温度的高。什么是温度?我们中学里将温度描述为“物体的冷热程度”。
物体的冷热程度是人体的一种知觉,每个人对于冷热的感受不一样。南方人通常比北方人耐热,有些人洗澡喜欢用40℃以上的水,有些人则觉得40℃以上太烫了。于是我们需要一个客观的、定量的定义来描述温度的高低。
温度是用一些处在恒定状态的物理系统来确定的。冰水混合物的温度被定义为0℃,一个大气压下水沸腾时的温度为100℃。定下0℃和100℃以后,把温度计100等分,就有了不同的温度的定义。
温度的微观定义
以上用温度计来做定义,测量的是物体的宏观温度性质。宏观物体是由微观粒子组成的,将温度具体分配到每个粒子上,在微观世界它的定义是什么呢?一个粒子的温度如何定义?
不如由一个物理现象出发,猜测一下从微观层面来定义的温度应该是什么样的。我相信你应该有过泡奶粉、泡咖啡或者泡茶的生活经验。要泡开它们都需要热水,如果用冷水是很难化开的。化开得快,本质是分子之间相互渗透的速度快。因为热水温度高,水分子运动速度快,所以化开得快。这就告诉我们,温度的本质跟分子的运动速度快慢有关,分子运动速度快体现为温度高。这样就引出了温度的微观定义,温度的高低,具体数值是多少现在不用在意,因为它无非是一个人为确定的标准而已。我们探究的是温度的本质。
温度的本质是微观粒子的运动,但如果用微观粒子的运动速度来定义温度是不方便的,为什么?因为速度是个矢量,它不光有大小,还有方向,但是温度是一个标量,它只有大小,没有方向。所以,可以把温度定义为正比于微观粒子运动动能的平均值,因为动能跟微观粒子运动速度的平方成正比,是一个只有大小,没有方向的量。
一个宏观物体的温度正比于组成它的所有粒子动能的平均值。这里的关键是平均值,也就是说温度是一个宏观概念,单个粒子不存在温度的概念,我们只能描述它的动能。假设现在有一罐氧气,它的温度是恒定的,为20℃。这里的20℃,就正比于所有氧气分子微观运动动能的平均值。但如果真的去观察每个氧气分子的运动,会发现它们还在碰来碰去,不可能每个分子的运动速度完全一样,所以它们的运动动能不可能完全相等。因此我们只能说,温度是正比于所有微观粒子运动动能的平均值。就像你问一个班级里学生的平均身高是多少,可能这个值是1.5m,但是不可能每个学生的身高都是精确的1.5m。[注:此处我们说温度正比于动能的平均值,是因为在这里还存在玻尔兹曼常数k,k≈1.38×10-23J/K(焦耳/开尔文,焦耳是能量单位,开尔文是温度单位)。温度T×玻尔兹曼常数k,给出的就是能量的单 位。]
因此,讨论微观系统,尤其是单个粒子或较少数量粒子的温度没有意义,我们只需要用动能就可以描述它。温度是一个统计概念,它用来描述的对象必须是一个系综,系综是指那些粒子数大到阿伏伽德罗常数数量级的系统。温度是一个用来研究多对象、大体系的物理量。它的研究对象里必须有非常多的个体,多到无法描述单个个体,而只能描述整体的平均性质。这就引出了热力学的适用范围,它研究的是巨大数量个体组成的整体性质,数量多达阿伏伽德罗常数的数量级。
真空中的温度是多少?
有了温度的微观定义,我们就会发现“温度是物体的冷热程度”这个描述是不够准确的,至少是不全面的。把一个温度计扔到一个地方,给出一个读数,这个读数未必是温度的定义。就像我问你真空的温度是多少,此处我们说的真空是理想的、真的空无一物的真空。我们知道,现实的真空是不空的(前文中描述的卡西米尔效应告诉我们真空中的虚粒子对让真空有“真空零点能”)。
理想真空温度是多少呢?科幻电影里经常有太空很冷的场景,生物到太空中会冻住。但是理想的真空是不存在温度的,因为没有粒子,没有东西在运动,那为什么感觉上很冷呢?
你拿一个温度计放在太空里,它会显示一个读数,这是因为有散热的效果。太空是空的,一盆热水放在太空里,它的热量会通过热辐射的方式散失掉。这个散热过程带走了能量,所以温度计的读数是低温,体感温度是很冷的。体感温度低只能说明散热效果好,它与温度低之间还是有一定区别的。就好比你光脚踩在瓷砖地面和木板地面上的时候,虽然二者温度肯定是一样的,但是明显感觉瓷砖地面更冷,因为瓷砖地面散热更快,能从你的脚上更快地带走热量。
可见,用物体的冷热程度来定义温度,并非一个抓住本质的定义。
什么是绝对零度?
大家一定听过一个概念,叫作绝对零度,而且绝对零度是达不到的。根据温度正比于粒子微观运动的动能平均值,我们把这个状况推到极限,当粒子完全不动,动能为零的时候,就应该对应于绝对零度。
根据热力学第三定律,绝对零度是无法达到的,这是一条原理性质的定律,并没有演绎性的证明。但如果我们把背景拓展到量子力学层面,尽管还不是很清楚,不确定性原理可能可以给出一些侧面的解释。
从不确定性原理的角度看来,因为粒子无法停止运动,它一定有最小限度的运动。不确定性原理说的是,一个符合量子力学规律的微观粒子,它的位置和速度无法同时确定。
如果一个粒子真的能够停止运动,说明它的速度为零,并且位置不会发生任何改变,那么它的位置和速度就被同时确定了,这就不满足不确定性原理了,因此不可能出现粒子完全停止运动的情况。当然,热力学讨论的粒子还是经典意义的粒子,它描述粒子的基本模型与量子力学是不一样的,所以不应这样简单草率地解释。热力学意义上的绝对零度不可达是一条原理性的结论。
虽然绝对零度达不到,但是我们可以定义一个数值给它。我们把粒子动能为0的那条线,定为绝对零度。然后以动能为0的点作为基准点,动能每增加一点,就定义增加一度。依此类推,这就是开尔文温度。
开尔文温度是以粒子的微观运动动能定出来的温度体系。所有热力学里的计算,都是依据开尔文温度,也叫热力学温度(thermodynamic temperature)进行的。开尔文温度和我们平时用的摄氏度有一个转换关系。0℃的冰水混合物里面的水分子还是有动能的,我们计算出0℃的水的动能,然后递减温度到绝对零度,就能得出换算关系——开尔文温度=摄氏度+273.15。
我们规定开尔文温度的温度间隔与摄氏度的温度间隔是一样的,也就是100开尔文比99开尔文高多少平均能量,100℃也比99℃高多少能量。绝对零度如果写成摄氏度,就是-273.15℃。除此之外,还有华氏温度(Farenheit),现在全世界范围内,绝大部分国家都使用摄氏温度,美国使用的是华氏温度,华氏温度与摄氏温度(摄氏度)的换算关系是F=9×C/5+32。所以当一个美国人在抱怨“天气太热,一定有100度”的时候,他并不是在夸大其词,因为华氏温度的100度大约是37.8℃,确实是很热。
第二节 理想气体(ideal gas)
热力学的研究对象
有了温度的定义,我们就可以开始进行热力学的研究了。
首先要明确热力学研究对象的范围。温度正比于一个系统内所有分子运动动能的平均值,所以,我们研究的对象必然是一个多粒子系统。几个粒子这种情况,我们用量子物理处理就可以了。阿伏伽德罗常数数量级的粒子系统,才是热力学的研究对象,因为热力学研究的都是整体的宏观性质,是做过平均值之后的性质。
所以你会发现,粒子极少的时候,我们有量子理论可以研究,粒子多的时候,我们可以用热力学,甚至量子场论研究。
热力学的适用范围
这就引出了热力学研究范围的第二个规定:除了粒子数量极其庞大之外,必须假设我们研究的是已经经过了极长的时间,达到了充分稳定态,不再发生变化的系统,这样的状态叫热力平衡(thermodynamic equilibrium)。像奶粉溶化在水中这样的过程,热力学是不研究的,因为里面的过程太复杂、参数太多,很难描述清楚。
因此,热力学的适用范围,我们已经确定:
(1)是要有阿伏伽德罗常数数量级个粒子的宏观系统;
(2)必须是热力平衡。
理想气体
设定了所研究系统的性质,再来看看我们现实生活中的真实研究对象是什么样的。现实中能接触到的物质基本有三种形态:固态、液态和气态。比如说水,固态是冰,液态是水,气态是水蒸气。
气体的体积在升温、降温的情况下会变化得很明显,而液体和固体的体积与温度的关系则不那么简单。我们通常关注液体的流体性质,是通过流体力学去研究的。对于固体,我们更加关注的是它的晶体结构、材料性质和电学性质。因此,“极热篇”主要讨论的是气体。
要研究气体的什么性质呢?我们现在有了温度的定义,就可以把温度当成一个最主要的参数,那就要看从气体的温度出发,还可以把它的哪些性质关联起来。气体有气压,大气的压强差不多是100 kPa,1Pa相当于1N的力平均分配在1m2的面积上。除了气压以外,我们也关注特定气体的体积和密度,这些都是气体的物理性质。除此之外,还有气体的化学性质。不同气体混合发生反应,会有反应速率的问题。这属于物理化学的研究范畴。
能够测量到的关于气体的物理量,有气压、体积、密度和温度。要想知道气体这几种性质之间有什么联系,它们的变化规律是什么样的,就需要用一个模型去描述它的行为。此处密度和体积其实是两个相互关联的量,同样质量的气体体积越小,密度就越大。所以,可以把密度换成气体的分子数。这样一来,这几个量就相互独立了。
既然要研究气体,就要构造一个可以用物理学进行定量研究的模型。对气体性质研究进展最为迅猛的时期是在19世纪,当时的很多物理学家、化学家都研究了气体的性质。比如我们在“极小篇”开篇讲过的英国化学家道尔顿,他证明了原子的存在。道尔顿对气体的研究贡献卓著,他提出了著名的道尔顿分压定律(Dalton's law of partial pressures)。该定律的大概意思是,把两种气体,比如二氧化碳和氮气,混合在一起以后,混合气体的总气压等于两种气体各自的气压之和。不光是两种气体,多种气体也满足这个定律。
根据一系列的经验定律,对于气体的研究有一个最好用的模型,叫理想气体模型。这个模型说的是:气体的气压×它的体积,正比于它的分子数×它的温度。这就是描述理想气体的方程式——克拉伯龙方程(Clapeyron equation)。
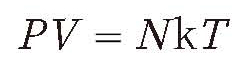
P:压强v:体积 N:粒子数 k:玻尔兹曼常数,1.38×10-23J/K T:温度
所谓理想气体,就是把这些气体分子当成完全独立的个体,假设气体的分子和分子之间没有任何相互作用,并且把气体分子当成完全弹性的小球,它们跟容器壁进行碰撞时完全没有能量损失,是弹性碰撞。
气体中分子间的距离非常大,相比之下分子的直径小到可以忽略。所以,气体分子间的碰撞概率非常小。我们可以假设气体分子之间没有显著的相互作用。这种假设虽然不能完全描述实际情况(实际情况是分子和分子之间不可能完全没有相互作用,它们也会相互碰撞和相互吸引),但之所以能做这个假设,是因为它是气体,气体分子之间的平均距离非常大,所以它们之间相互作用的影响很小,因此,即便忽略了这种相互作用,也不会对结果有重大的影响。
而液体和固体肯定是不能做这样的假设的。液体有一个现象,叫表面张力(surface tension)。比方说,一杯水完全倒满,哪怕水的表面比杯子表面高一点点,它也不会溢出来,靠的就是水的表面张力,它表现为水的黏性,这就是水分子之间的作用力,因此对于液体不能忽略分子之间的作用力。对于固体就更加不能了,固体之所以为固体,就是因为分子间作用力占据主导,分子的自由运动无法打破固体的固定结构。
理想气体模型的有效性
我们可以根据生活经验,或者物理直觉,来检验一下克拉伯龙方程。假设现在有一罐气体,罐子的大小是不变的。假设罐体密封很好,不会有气体进出,根据生活经验,给这罐气体加热,内部压强肯定会增大。在克拉伯龙方程里,V不变,T升高,则P肯定增大,所以理想气体方程能描述这个现象。
假设温度一直不变,可以把罐子放在恒定温度的水里以保持恒温,然后缓慢往罐子里充气。这里必须强调缓慢,因为热力学研究的是稳定态的系统。缓慢充气可以保持作用过程中温度一直恒定,气充得越多,压强也越大。所以在体积恒定的情况下,气压和分子数成正相关。克拉伯龙方程里,T不变,N增大,则P也增大。
如果这个罐子是可以压缩的,我们想办法把这个罐子的体积压小,其实就是让气体的体积减小,压缩以后,气压会随之增大。也就是说,在温度恒定、粒子数恒定的情况下,体积越小,气压越大。在克拉伯龙方程里,对应的就是T不变,N不变,V减小,则P必须增大。
这样,我们就验证了克拉伯龙方程至少在几个物理性质之间定性的关系上是一致的。理想气体满足的克拉伯龙方程,是可以充分描述理想气体的行为的,它跟我们实际的气体也相差不大。
第三节 如何从微观上理解气体
压强的本质
理想气体的行为是由克拉伯龙方程把几个气体的宏观性质联系起来进行描述的。但是本质上,这些都是由理想气体中微观粒子的性质综合得来的。所以,我们要从微观粒子的性质出发来解释宏观性质。只有从微观性质出发推导出来的宏观性质,才能说是演绎的结论,才能从本质上理解气体的行为。
首先我们来讨论一下,气体压强的本质是什么?一个罐子里装着气体,气体有扩散的趋势,但是被罐子束缚住了,所以感觉罐子的内壁上会有气压。
那么从微观层面看,气压是什么呢?我们说有温度,是因为微观粒子在做无规则运动。罐子的内壁不断有粒子在撞击它,这种快速且频率非常高的撞击在宏观看来就变成了一个持续的力,这种撞击力的感受就是气压,气压的本质就是微观粒子存在运动。这个压强如此稳定,恰恰是因为我们研究的是稳定态的理想气体。
那么气压怎么算呢?在“极快篇”第三章,我们曾经计算过空气阻力正比于速度的平方。这里的计算完全相同,只不过在计算压强的时候,空气分子碰撞容器壁的速度是各个方向都有的,不像风阻将空气的流速视为一个方向。我们要做的是取一个平均值,因为对于稳定气体,我们关心的都是平均值,所以我们要得到的是空气分子撞击罐子内壁的力的平均值,也就是单个分子撞击容器壁的力正比于它速度的平方。
速度的平方又正比于什么呢?当然是它的动能,因为动能就是质量乘以速度的平方再除以2。压强就是正比于单位时间内所有分子撞击容器壁单位面积的动能的平均值。分子动能的平均值又是什么?这不就是我们前面说的正比于气体的温度吗?经过一系列推理,单位面积压力,也就是压强,正比于温度。分子数量越多,压强越大,因为敲击的次数多,所以压强正比于气体分子数。由此,我们就大致验证了理想气体方程的形式。
范德瓦耳斯力(van der waals force)
在实际情况当中,理想气体真的完全准确吗?未必。理想气体的模型有个基本假设,就是气体分子之间没有相互作用。因为气体分子之间的距离很大,所以分子之间碰撞的概率不大,但是不大并不等于不存在。分子靠近之后,除了碰撞,还有其他相互作用力。比如,我们把碳和氧混合在一起,温度高一点儿,它们就会发生反应形成二氧化碳。也就是说气体分子之间不可能没有相互作用,否则化学反应也不可能发生。分子和分子之间除了碰撞以外,肯定还有其他的相互作用。
这就引出了一个概念——范德瓦耳斯力。每个分子由原子组成,原子里又有电子和原子核。两个原子靠近,它们各自的电子之间有电磁相互作用,也会互相感受到对方原子核的作用。因此分子间肯定有电磁相互作用,只不过分子、原子的结构导致这种相互作用的总效果比较复杂。
范德瓦耳斯力是由一个叫范德瓦耳斯的荷兰科学家于19世纪后半叶提出的。他认为在分子层面上,普遍存在复杂的相互作用规律。当然,这种力只是电磁力在比较复杂的电荷分布情况下给出的一个集中的总效果。因此它的形式比较复杂,在不同距离上规律不一样,有吸引的表现,也有排斥的表现。这就是我们中学学过,但是老师没有详细解释的分子间作用力。比如,壁虎可以在墙壁和天花板上爬,靠的就是脚趾和墙壁分子之间的范德瓦耳斯力。
范德瓦耳斯力也可以解释不同的化学键的性质差异为什么那么大。当然,本质上它们都是量子力学层面电子波函数的不同表现形式。
如果我们考虑范德瓦耳斯力,理想气体的描述就不准确了,尤其在气体密度很大的情况下,理想气体模型就会越发不准确。
但其实如果考虑了范德瓦耳斯力,它的效果也不过是对理想气体方程的形式有一点修正而已。因为我们分析气压的那部分,从原理上来说依然是适用的,它依然是气体分子撞击容器壁的过程,因此我们可以想象,范德瓦耳斯力的引入,无非是让理想气体的方程式有一定的修正而已。
修正的物理量是什么呢?很明显分子数是不会变的,温度是我们的一个参数,也不用变。在同样分子数、温度恒定的情况下,气体由于存在范德瓦耳斯力的吸引,它的体积会倾向于缩小。体积缩小的情况下,压强应当会增大一些。因此,范德瓦耳斯气体方程跟克拉伯龙方程比,只是有一些修正。但是在体积特别大,气体密度特别小的情况下,范德瓦耳斯方程的修正是可以被忽略的。
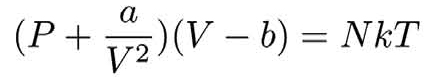
a和b是两个需要测量的修正数值,它们与系统中的粒子数N有关。
至此可以说,我们对于恒温、稳态的气体的研究已经比较全面了。它的气压、体积、分子数和温度之间的联系已经非常明白。但它只是气体的静态性质,真实世界的气体都是流动的,都处在动态,哪怕不是动态,也并非温度都一样的稳态。微观气体分子的运动也是多变的,所以我们要尝试对动态的宏观气体以及微观的气体分子规律进行进一步研究。
第四节 用统计学理解热力学系统
掷骰子
我们已经理解了气体的稳定态有什么样的性质。总的来说,可以用理想气体方程式来描述它的宏观性质,当然,更加精确的模型是范德瓦耳斯气体模型,它在理想气体的基础上,对于压强和气体体积做了一些修正。
但是,宏观也是由微观构成的。在气体的稳定态下,微观粒子的状态是稳定的吗?来看一个生活中的例子。
假设你去掷骰子,会得到从1至6其中一个结果。那么掷10个骰子全部得到1的概率是多少呢?(1/6)10,一个很小的数字。如果是100个呢?1000个呢?全部都是一样点数的概率就更小了。
随着骰子的数量增多,最终的结果会呈现什么样的规律呢?掷的骰子数量越多,比如掷10万、100万个,最终的结果一定是出现1—6这6个结果的数量基本相同。
大数定律(law of large numbers)
掷骰子是一个随机过程,获得1—6这6个结果的概率都是1/6。这里就要介绍大数定律:当一个随机过程的样本数量越大,最终得到的结果就越接近这个随机过程的概率分布。比如你掷6次骰子,最后点数分别是1—6点,6个结果的概率是非常小的。但如果你继续掷,掷60次、600次、6000次,掷的次数越多,样本数量越大,最终的结果就应该越接近概率的分布。掷骰子的概率分布就是每个结果对应1/6的概率。
再来看看气体,气体的温度正比于它所有粒子运动动能的平均值。如果单看一个气体粒子,可以说它在做无规则运动。对于处在恒温的一个体系内的气体分子,绝不可能每个分子都精确地以同一个动能在运动,但是它们的平均值却是确定的。这说明虽然单个粒子的运动可能毫无规律,但是总体来看一定是有规律的。
在“极小篇”中我们说过,之所以用概率波来描述粒子的运动状态,是因为单个粒子的运动杂乱无章,但在整体上呈现为一个概率的分布。气体也应该一样,虽然目前还没有引入量子力学的规律,它们从个体上看没有什么规律,但是整体上,一罐恒温气体中的气体分子所具有的运动动能应当满足一个概率分布。我们可以说某个动能范围内分子的数量占总分子数量的百分比是多少,这就是气体的动能或者说速度分布函数。
根据大数定律,宏观气体中的分子数量极其巨大。它的分布函数应该是相当稳定的,如果真的测量每个分子的运动动能,得出的实际情况应当与这个分布函数相吻合。正是因为宏观事物中微观粒子的数量极其庞大,所以我们可以非常放心地使用分布函数来描述它们的性质。
我们虽然无法具体描述单个粒子的行为,但可以知道它们行为的分布。如果气体所有分子的动能有一个分布状态,它应该是什么样的呢?这个分布状态又是依据什么原则来确定的呢?
热力学第二定律
此处,我们就引出了一条热力学当中最核心的定律——热力学第二定律。这条定律可以说是目前物理学中最核心的铁律之一。
热力学第二定律最主要的表述方式有两种,分别是从宏观层面和微观层面来描述的。宏观层面的表述叫克劳修斯表述。克劳修斯是19世纪的一位物理学家。克劳修斯表述是这样的:热量无法自发地从低温物体流向高温物体而不产生其他影响。第二种表述是微观表述,也叫玻尔兹曼表述,说的是一个封闭系统的熵永远不会自发减小。所以,热力学第二定律也叫熵增定律。
第一种表述很好理解,你拿一个热的东西和冷的东西接触,热量一定会自发地从热的东西流向冷的东西,直到二者温度相同,热量才会停止流动。这又对应了热力学第零定律:两个温度不同的物体进行热量交换,最终的结果一定是两个物体的温度相等。除非是空调这种非自发的情况,你会发现空调外面的压缩机会散发出很多热量,也就是空调制冷需要外部输入能量才能做到,它并不是一个自发过程。
第二种表述提到了一个概念,叫作熵,它是表征一个系统混乱程度的物理量。
总的来说,一个稳态的热力学系统,它的熵一定处于可能的最大的状态。有了这条热力学系统的第一性原理,我们就能够求出宏观系统里微观粒子动能的分布规律了。这些微观粒子的速度分布,必须要满足一个条件,它一定是所有可能的分布中让系统总体的熵最大的一种。
到底什么是熵,如何定量地衡量一个系统的混乱程度呢?
第五节 熵增定律
什么是熵?
熵是一个用来描述物理系统混乱程度的物理量,一个系统越混乱,它的熵就越高。一个没有能量的输入和输出,处在封闭状态的系统,它的熵在自发演化的过程中永远不会主动减小,这就是熵增定律。

图15-1 玻尔兹曼的墓志铭:S=k logW
就像房间如果不打扫,就会越来越乱,这里的打扫就相当于给房间输入能量,打扫房间的能量需要通过吃饭来补充。但是这里房间的混乱与否,完全取决于个人的主观感受。
物理学是如何定义一个系统是否混乱呢?19世纪末著名的奥地利物理学家玻尔兹曼提出,熵最根本的定义与微观态数有关,其微观定义表达式是S=k logW(k是玻尔兹曼常数,W是微观态数)。
什么是微观态数呢?它是指一个系统可能存在的状态的个数。举个例子,现在有一高一矮两个玻璃杯,我给你一颗绿豆,绿豆必须在杯子里。那么这两个杯子和一颗绿豆组成的系统,有几种可能的状态?答案是两种,绿豆必须在其中一个杯子里。如果多一个不同的杯子呢?那样就会有三种状态。如果再多一颗绿豆呢?答案是六种,两颗绿豆在同一个杯子里,这就有了三种情况,也可以将绿豆分别放在两个不同杯子里,也就是有一个空杯子,也有三种情况。
这里我们假设两颗绿豆完全一样,所以不存在两颗绿豆发生交换,会产生两个不同状态的情况。随着杯子和绿豆的数量增多,这个系统可能存在的状态会越来越多。有多少种摆绿豆的方法,就对应多少种系统的微观态数。微观态数的对数×玻尔兹曼常数,就是熵的微观定义。那我们可以看看,如果一个系统只有一种状态,那么熵是多少?答案是0,klog1=0。
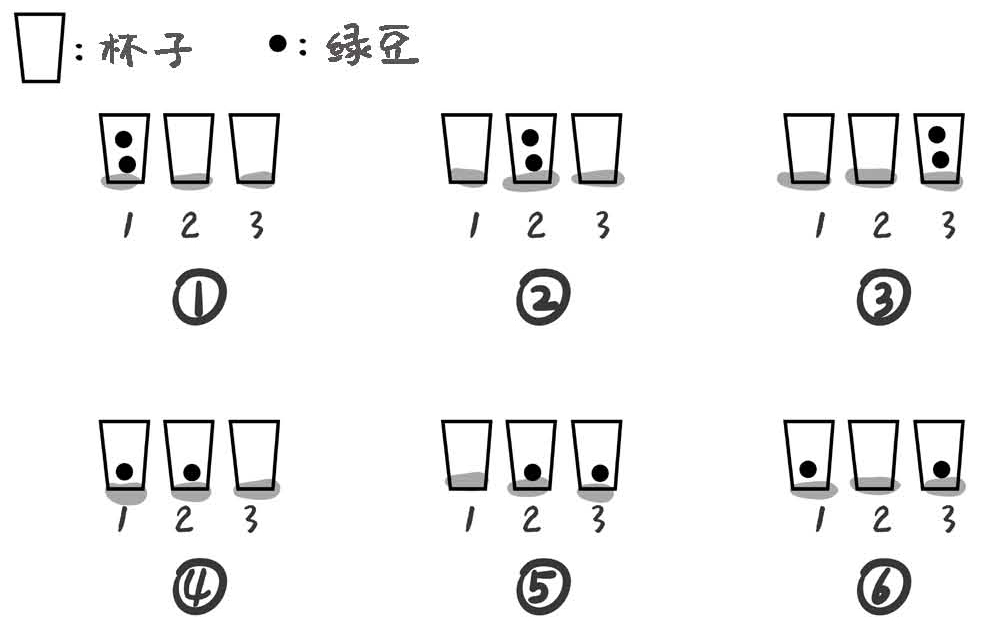
图15-2 绿豆游戏
类比玻璃杯和绿豆的例子,对于一个系统的气体来说会怎么样呢?把气体分子可能处在不同的能量状态的数量,类比于上面例子里杯子的数量,气体分子可以达到的能量状态越多,就好比杯子越多。把气体分子比作绿豆,气体分子数量越多,就好比绿豆的数量越多。
分子动能的分布
有了熵的定义,就可以讲什么是熵增定律了。熵增定律说的是,一个封闭系统的熵无法自发减小,随着时间的推移,一个系统达到的最稳定的状态,一定是这个系统可能存在的熵的最大的状态。这就是熵增定律,也叫热力学第二定律。
有了熵增定律,就能回答上一节的核心问题了:处在稳定态的气体分子的运动速度大小的分布是什么样的?答案是麦克斯韦速率分布(它的形态与常见的正态分布较为相像)。麦克斯韦速率分布是两边小,中间大的分布函数。速度大小刚好在气体分子平均速度(对应平均动能)附近的分子数是最多的,速度特别小和特别大的粒子数都比较少。
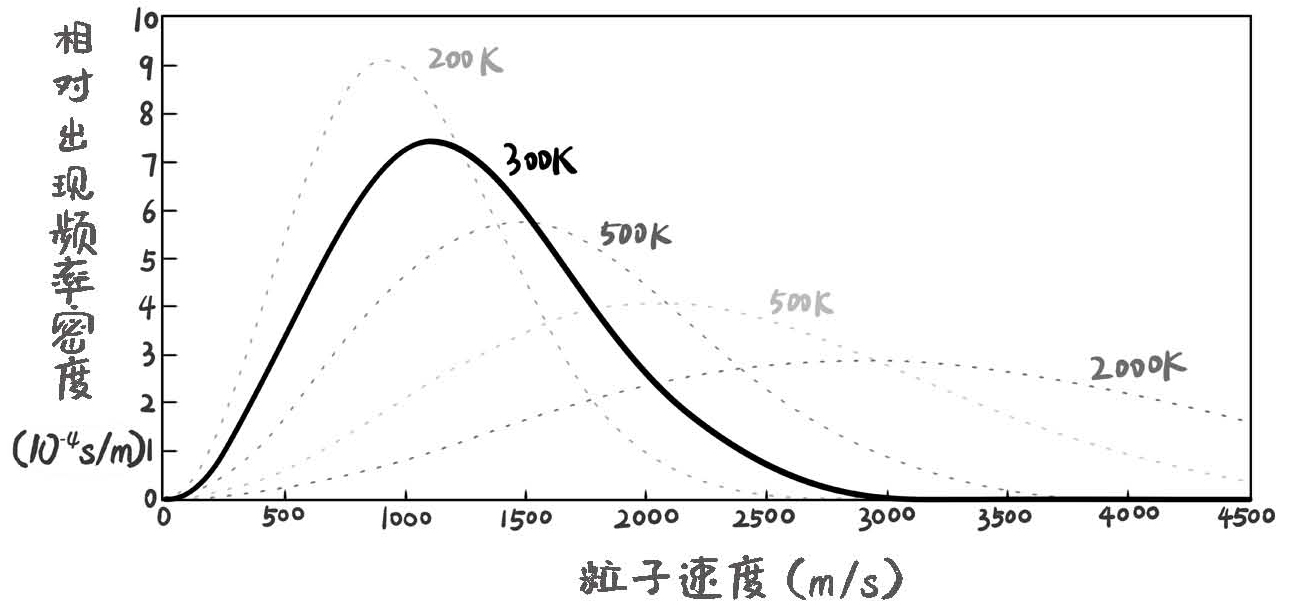
图15-3 不同温度下,粒子速度的分布图
为什么是这样的分布函数?因为在这种分布方式下,气体总体的熵才是最大的。这就是通过熵增定律推导出来的微观层面气体分子的速度分布的最重要的规律。
熵增定律的普适性
这只是通过熵增定律得出的气体分子运动动能的分布。但原则上,通过熵增定律可以得出任何稳态统计学系统的能量分布,并不局限于气体、液体、固体,它们都满足熵增定律。它是普适的定律,在一切条件下都成立,科学家至今没有发现过违反热力学第二定律的现象。
对于任何一个热力学系统,都可以通过写出它的微观态数,算出它的熵,从而得出让熵最大化的办法。这里就对应了玻尔兹曼分布,即一个系统内微观的部分可能有各种能量状态,与平均能量差得越多的能量状态,在整个系统里的占比就越低。一个能量状态在整个系统里的占比,跟整体系统的温度以及这种特定能量状态的能量大小有关。
有了这个分布,我们就可以计算系统里的各种物理性质。一个系统里可以有各种各样的物理参数,比如给一块材料加一个磁场,那么这个磁场就会跟材料里的原子发生关联,这种关联会影响到整个材料的能量。最终这块材料所表现出来的整体磁性,就是把里面所有可能出现的磁性所对应的能量按照玻尔兹曼分布求和,再取平均值得到的结果。
至此,我们对热力学的基本思想,以及统计力学里的基本原理做了介绍。热力学和统计力学研究的是同一种物理学系统,只不过它们的方法论不同。热力学是从现象出发,通过热力学系统的宏观性质预言它的行为;统计力学则是从微观出发,先定义诸如熵这一类的物理量,再从微观构造宏观,比如气体的能量分布函数。二者实际上是相互融合的,我们也可以认为热力学是统计力学的前身。因此,热力学作为一门独立学科,它在现代物理学中的地位几乎已经被统计力学取代了。
