第六章 万有引力
第一节 天体运动的第一因:万有引力
真实的宇宙,是所有天体在同一个时空背景下进行着相互作用,比如地球绕着太阳转,月亮绕着地球转。天体间最主要的相互作用有且只有一个,就是万有引力。那么万有引力都与哪些因素相关?以及在万有引力的作用下,天体的运动会呈现出什么样的规律呢?
为什么月亮不会落地?
万有引力的发现者是牛顿[另一说是英国科学家胡克(Robert Hooke)]。牛顿是英国人,活跃在17世纪后半叶,可以说他是所有物理学家的鼻祖。民间广为流传着一个故事,就是牛顿是因为被一个熟透的苹果砸到了头,才灵机一动,想到了万有引力的存在。
相信被苹果砸到头的也不止牛顿一个,为什么只有牛顿提出了万有引力定律呢?这要追溯到牛顿著名的力学三定律(Newton's law ofmotion)。牛顿第一定律说的是,一个物体在没有外力作用的情况下,要么保持静止,要么保持匀速直线运动的状态。简单来说,就是一个物体的运动状态如果发生了改变,一定是有力作用在了上面。
在空中放开任何重物,都会落到地面上。它从静止到下落,运动状态发生了改变。根据牛顿第一定律,一定是有力作用在了苹果上,且这个力是指向地面的。
图6-1 牛顿与苹果的邂逅(此故事是否真实目前无法确定,且有资料表明其很有可能是牛顿在与胡克争抢发现万有引力定律荣誉时,所编造出的少年时期就受到启发的故事)
既然苹果会受到地球的引力作用下落,那么挂在天上的月亮,也应该受到地球的引力才对,为什么月球不会落到地面上呢?答案是因为月球在围绕着地球转动。而月球之所以会围绕地球转动,恰恰是因为地球对月球有吸引力,否则的话,月球早就飞离地球了。
比如用一根绳子绑住一个重物,然后拉着绳子让重物转起来,转得越快,绳子被拽得越紧。绳子的张力就好像地球对月球的引力,维持着重物的圆周运动;如果绳子断了,这股力就不存在了,重物就会飞出去。
牛顿由此推断,地球和月球之间一定存在万有引力,否则月球不会围绕地球转圈。那么牛顿的下一个任务,就是去寻找万物间引力的数学变化形式,它跟什么因素有关,是什么决定了引力的大小和方向。
如何得出万有引力定律?
牛顿有一句名言:“我之所以比别人看得远,那是因为我站在了巨人的肩膀上。”牛顿这句话并不是谦虚,事实确实如此。
牛顿至少站在了两位巨人的肩膀上,一位是伽利略,另一位则是与伽利略同时代的天文学家开普勒。
早在牛顿之前,开普勒继承了老师第谷(Tycho Brahe)的天文观测工作。师徒俩加起来坚持了近30年,得到了上万组天体运动的数据。
在没有任何理论指导的情况下,开普勒单纯依靠观测结果,发现了天体运动的轨道是椭圆形,并总结出了开普勒天体运动三定律(Kepler's laws of planetarymotion):
(1)椭圆定律:所有行星围绕太阳运动的轨道都是椭圆,太阳在椭圆的一个焦点上;
(2)面积定律:行星和太阳的连线在相等的时间间隔内扫过的面积相等;
(3)调和定律:所有行星绕太阳一周周期的平方与它们轨道半长轴的立方成正比。
正是这三定律,让牛顿写出了著名的万有引力公式:
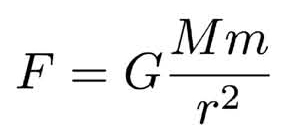
这个公式说的是,任何两个物体之间的引力,正比于二者的质量,反比于二者之间距离的平方。也就是说,如果两个物体之间的距离扩大一倍,它们之间的引力会变为原来的四分之一。
除此之外,万有引力的方向是径向的(radial),并没有切向力(tangential force)。径向就是二者位置连线的方向,而切向则是跟二者连线垂直的方向。比如地球围绕太阳运动时,太阳对地球的引力只指向太阳,不会指向其他方向。

图6-2 开普勒(1571—1630)
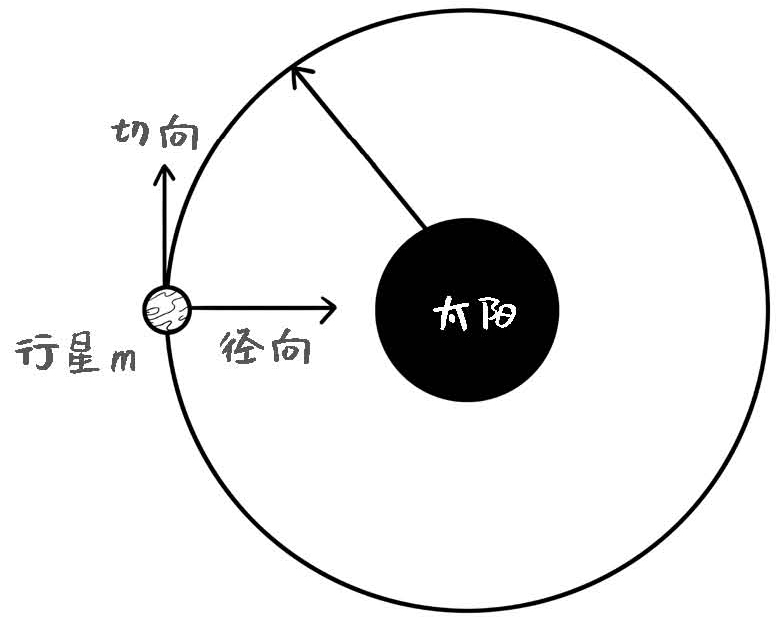
图6-3 万有引力的径向力
牛顿是如何总结出上面这些规律的呢?其实那个时候,牛顿已经隐约感觉到两个物体之间的引力大小,应该是跟距离的平方成反比关系。
通过计算,牛顿了解了一个事实:地球表面物体受到的重力加速度,是月亮围绕地球旋转的向心加速度的3600倍。而那个时候,人们已经知道地球和月球的距离,差不多是地球半径的60倍。602刚好是3600,所以一个距离平方反比关系就浮现了出来。牛顿后来将平方反比的规律代入万有引力的公式,经过计算,发现确实能推导出一个椭圆轨道。
万有引力与质量的关系,则是牛顿通过牛顿第三定律,再结合当时广为人知的伽利略关于两个不同重量的球同时落地的结论,推导出来的。
第二节 站在伽利略肩膀上的牛顿:引力公式
引力和距离的平方成反比
开普勒第一定律说的是,所有行星绕太阳运动的轨道都是椭圆形,并且太阳刚好处于椭圆的一个焦点上。而行星会绕太阳运动,是因为太阳和行星之间的万有引力。那么很自然会引出一个问题:什么样的万有引力会产生椭圆轨道呢?是离得越远引力越大,还是离得越远,引力越小?或者引力是一个恒定不变的值,跟距离没关系?
根据计算,两种形式的力会产生椭圆轨道。一种就是我们熟知的平方反比关系,另一种则是当引力跟距离成正比的时候,也会产生椭圆轨迹。但是不要忘了,开普勒第一定律还有后半句:太阳处在椭圆的一个焦点上,这就把第二种引力大小正比于距离的可能性排除了。因为刚才第二种引力形式,虽然轨道仍然是椭圆,但太阳必须处在椭圆的中心,而不是焦点。
牛顿之后,有人系统地总结了引力与距离的关系。如果引力不是上述两种形式的话,会产生奇形怪状的运动轨迹,很多轨迹甚至不是封闭的。
如果把科学精神发挥到极致,我们可以钻牛角尖般地想一下:为什么万有引力刚好正比于距离的平方?为什么不能是2.0000000012?为什么不会离2有一个极小的偏差呢?
由于这个偏差非常小,似乎并不会影响上面得出的结论,也不会影响椭圆轨道的近似闭合。那凭什么这个数值要精确地等于2?宇宙的规律就这么完美吗?这个问题从实验测量的角度是无法回答的,因为一切测量都有误差。设计得再精巧的实验也没有办法给出十足的证据,说这个值一定是2。
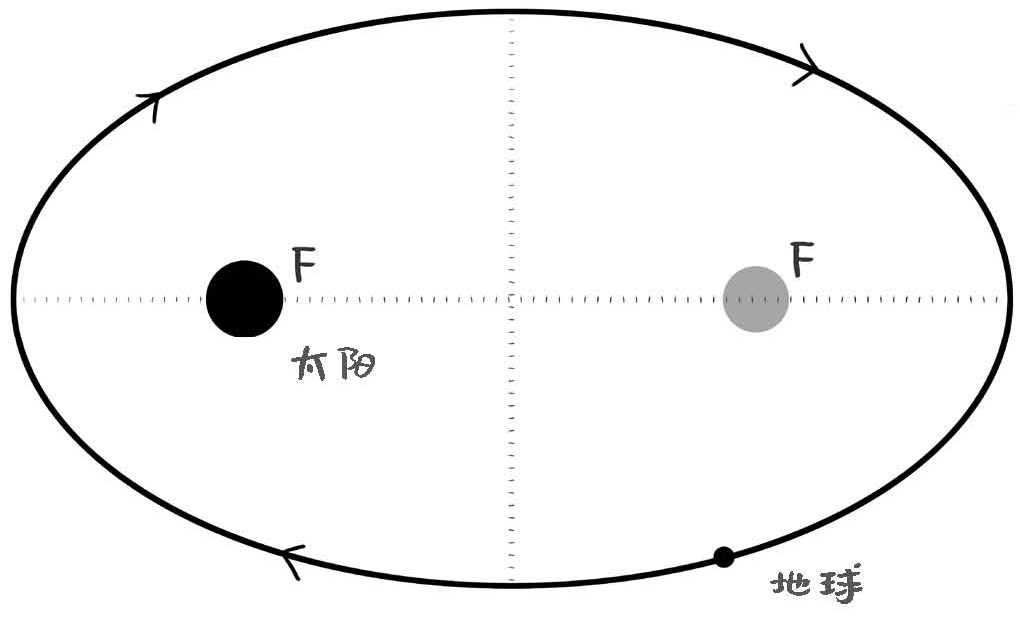
图6-4 太阳位于椭圆的一个焦点
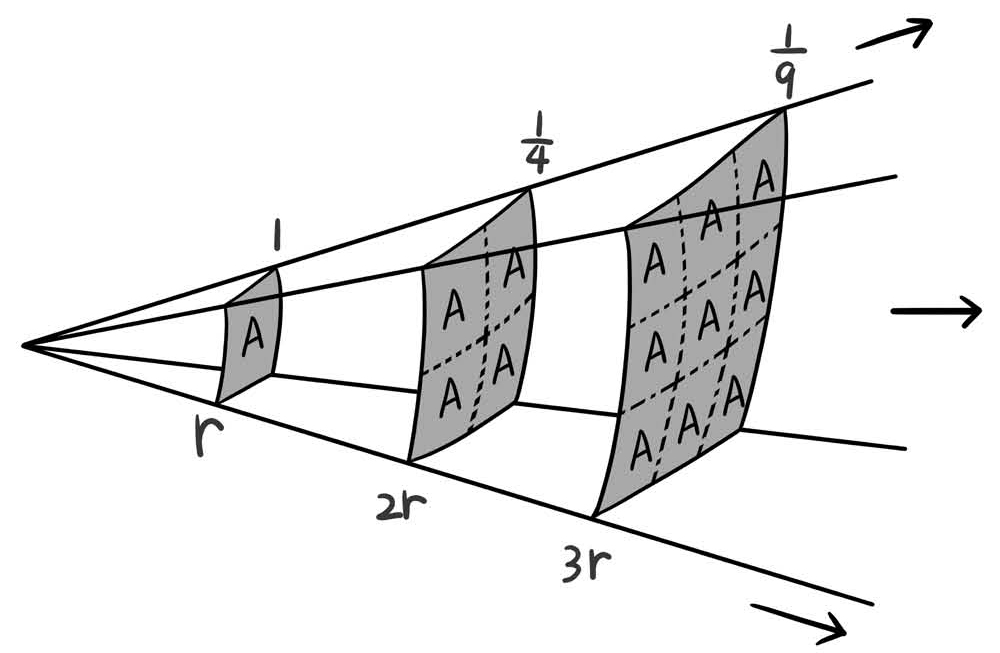
图6-5 引力线密度与面积成反比
但是我们可以从几何学的视角来看待这个问题。之所以距离上面的指数精确地等于2,恰恰是因为我们的空间是三维的。首先思考一个问题:地球是如何感受到太阳的引力的?我们假设地球能感受到太阳的引力,是因为太阳向地球发出了“引力线”。
然后可以引入一个概念,叫引力线密度,也就是单位面积内引力线的条数。引力线密度就代表了引力的强度,引力线越密集,引力就越强。假定太阳发射的引力线的数量是固定的,那么可以想象,离太阳越远,引力线就越稀疏。因为引力线是以太阳为中心,辐射状发射出去的。
现在我们要数一数太阳一共发出了多少条引力线,怎么办呢?我们可以从离太阳任意远的位置开始画一个大球面,把太阳给包住,然后数这个球面上一共有多少条引力线射出。很显然,无论离太阳多远画一个球面,都能把所有的引力线包住,因为引力线总的数量是不变的。就好像开着水龙头,然后拿杯子接水。不管贴着水龙头接,还是在水龙头下面远一点儿的地方接,单位时间内接到的水的量是一样的。
根据简单的几何学知识,一个圆球的表面积是=4πr2。而引力线的总量=某个球面的表面积×该球面位置引力线的密度,也就是引力的强度。
为了保证引力线的总量不变,也就是表面积乘以引力线密度后得到的结果跟半径无关,引力线的强度就只能是平方反比,否则引力线的总量就不守恒了。因此从几何学的角度来看,引力跟距离确实应该是精确的平方反比关系。
而得出这些结果的前提,恰恰是我们的空间是三维的,因为只有在三维空间当中,球的表面积才跟半径的平方成正比。可以想象,如果我们的空间不是三维,而是二维的话,那万有引力应该是跟距离成反比;空间是四维的话,引力则应该是与距离的三次方成反比。
引力只能是径向的
知道了引力的大小,还要回答一个问题:为什么引力只能沿着物体连线的方向?为什么不能有切向力的存在?也就是说为什么两个物体间的万有引力只会让它们前后运动,而不会让它们左右运动?
一个明显的证据就是,在地面上静止释放一个物体,它会掉到自己的正下方,并不会拥有水平方向的运动速度,所以在离地面比较近的地方,引力的方向看上去是指向地球球心的。
但是严格来说,这个推理是有问题的。因为地球有自转,地球表面的物体会受到地转偏向力的影响,台风和气旋就是这样产生的,所以即便不考虑被风吹的情况,一个物体也不会掉到正下方。光从地球表面释放重物的结果来看,并不能严格说明引力一定是径向的。
这样,我们就必须把尺度放大到行星的运行轨道,才能知道万有引力到底有没有切向力的部分。
开普勒第二定律
要回答万有引力是否有切向力这个问题,就必须要借助开普勒第二定律:太阳和行星的连线在单位时间内扫过的面积是一定的。
如果我们画一条线把太阳和行星连起来,随着行星的运行,这条线会在空间中扫过一定面积。行星转一圈,就刚好扫过一个椭圆的面积。也就是说,当行星离太阳远的时候,它的运动速度会变慢;当它离太阳近的时候,它的运动速度又会变快。
有了这条定律,我们就会发现引力只能是径向的。
因为如果有切向力存在的话,行星要么一直加速,要么一直减速,就好像有一个力一直牵引它,或者阻碍它前进一样。如果是这样,就不会出现面积速度恒定的现象。因为一旦有一个切向力一直拽着行星加速的话,它的切向速度会随着远离太阳而越来越快,单位时间内扫过的面积就会越来越大。减速情况下得出的结论刚好相反。所以无论是哪一种情况,开普勒第二定律都不会成立,引力的方向不可能是切向的。
在牛顿力学体系里,开普勒第二定律后来被总结为天体系统的“角动量守恒”。意思是对于天体系统,每个天体的质量乘以速度再乘以运动的瞬时半径,是一个守恒量。通常行星的质量是不变的,而速度乘以运动的瞬时半径,刚好就是开普勒第二定律里说的面积速度。
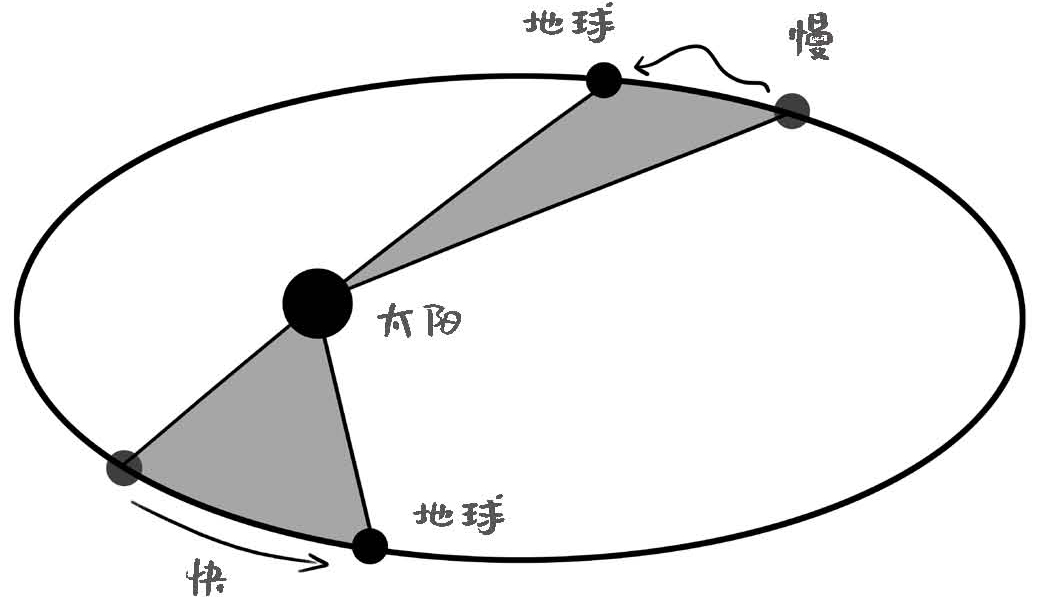
图6-6 开普勒第二定律中的面积速度
引力与质量的关系
万有引力不仅与距离有关,还与引力双方的质量成正比。要了解万有引力与质量的关系,就需要借助伽利略的研究成果。
伽利略曾经做过一个物体的自由落体实验:他站在比萨斜塔上,同时释放了一个铁球和一个木球,结果两个球同时落地。这个实验证明了物体的下落速度跟质量无关。
那么既然整个下落过程中速度与质量无关,就不难推导出加速度也与质量无关,万有引力与质量的关系就近在眼前了。
提到加速度,就要说到牛顿第二定律:一个物体的加速度乘以这个物体的质量,就等于这个物体所受的合外力,即F=ma。
加速度a就是物体在单位时间内速度的变化,比如一辆车在1s之内,速度从10m/s加速到11m/s,那它的加速度就是1m/s除以1s,也就是1m/s2。
引力与质量成正比
一个物体下落时所受的力就只有万有引力。如果下落的加速度与质量无关的话,就说明物体受到的引力除以它的质量是一个定值。
因为F=ma就意味着a=F/m,a与m没有关系,就说明在万有引力的形式中,引力的大小F必然与物体的质量成正比。然而,根据牛顿第三定律,万有引力的作用是相互的。当太阳的引力作用在地球上时,太阳也会受到地球给予的一个大小相同、方向相反的吸引力。
根据同样的推理,既然地球受到太阳的引力正比于地球的质量,那么反过来,太阳受到地球的引力也必然正比于太阳的质量,且二者大小相等,方向相反。
于是就可以得出结论:两个物体之间的引力同时正比于两个物体的质量。最后再把万有引力与距离之间的关系融合进去,就可以得出完整的万有引力公式:万有引力正比于二者质量的乘积,反比于二者距离的平方,且力的方向沿着二者连线的方向。
第三节 开普勒告诉牛顿:万有引力常数的测量
万有引力有多弱?
总结出万有引力的数学规律之后,还有最后一个问题:万有引力常数G是多少?因为G的大小直接决定了万有引力的强弱。其实G是一个非常小的数字,约等于6.67×10-11N·m2/kg2。
万有引力非常弱这一点,从生活当中就不难看出。假设有一个铁螺丝钉掉在地上,它是因为受到了地球引力的作用。这个时候,你可用一块非常小的磁铁就可以轻松地把小铁钉从地上吸起来,也就是说,一块非常小的磁铁所产生的磁力,就能轻松打败偌大一个地球产生的引力。所以可以粗略地认为,地球比一块小磁铁大多少倍,引力就比磁力小多少倍,这样就表明万有引力常数G是一个很小的数字。
那么,这么小的万有引力常数值是怎么测量的呢?其实如此精密的测量,并不需要现代科技的诞生。早在18世纪末,英国科学家卡文迪许(Henry Cavendish)就设计出了测量万有引力常数的实验——扭称实验。
这个功劳属不属于卡文迪许其实还有争议,因为卡文迪许并没有直接测量万有引力常数,他测量的是地球的密度(其实只要测出了地球密度,就能推算出万有引力常数的大小)。

图6-7 卡文迪许(1731—1810)
扭称实验
那这个实验具体是怎么做的呢?卡文迪许用到了一个工具,叫作扭称(torsion balance),这是由一个叫米歇尔(Johnmichell)的地理学家发明的。扭称在旋转的时候会产生弹性,可以认为它是一个旋转的弹簧。
当给扭称施加力矩(torque)的时候,扭称会发生偏转。通过读出扭称偏转的角度,就能知道有多大的力矩施加在了扭称上。力矩等于力乘以力臂,所以只要算出力矩,再除以力臂的长度,就可以知道施加的外力是多少了。
如果要在地球上测量引力的微弱效果,就要让引力尽可能大一些。卡文迪许的做法是选两个直径30 cm,重158kg的铅球作为引力的发生源;再用两个直径5 cm左右,重0.73kg的空心球作为研究对象;最后把这两个空心球用一根棍子连起来,棍子的中心吊在扭称下。
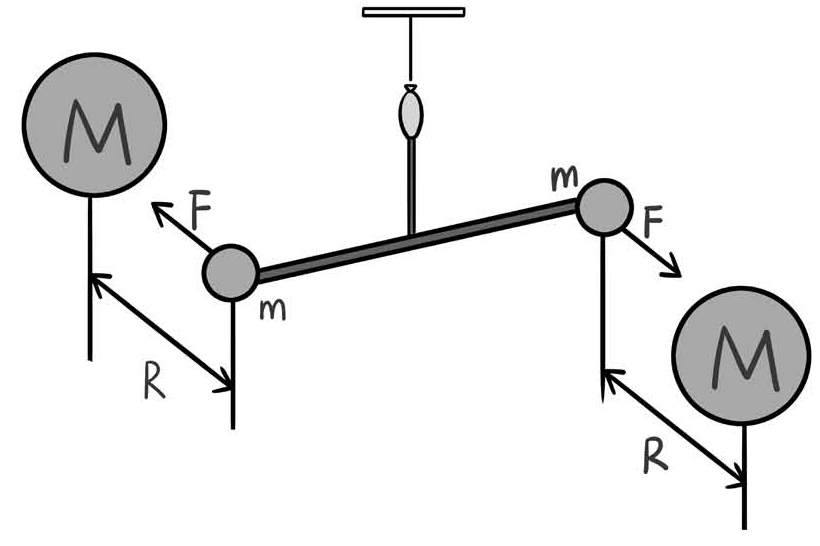
图6-8 扭称实验原理
根据万有引力定律,空心球和棍子组成的系统,会在大铅球的引力作用下发生一定角度的偏转。通过偏转的角度,可以计算出空心球受到的引力。
当时已经知道地球的半径有多大,用大铅球的引力和地球的引力做对比,就能知道地球的密度是多少。卡文迪许测算出地球的密度约为5.4 g/ml,大概是铁的80%,由此可以推测出地球的内核大概是金属物质。
卡文迪许实验的初衷并不是要去测量万有引力常数G,而是要测算地球的质量和密度。但只要有质量和密度,再根据牛顿的万有引力公式,就能计算出万有引力常数的大小。
为了让实验精确,卡文迪许排除了一切可能的干扰。首先这个实验的尺度要比较大,所以必须用很重的铅球;并且因为引力十分微弱,扭称要做得非常松,才能在微弱的引力之下发生扭转;为了排除空气流动和温度的干扰,卡文迪许专门打造了一个长、宽、高都是3m,厚度达60 cm的大木盒子。
在测量的时候,为了不干扰仪器,人不能站在盒子周围直接读数据,而是要通过木盒上开的两个口,用望远镜对读数进行观察。经过一系列的准备,卡文迪许观察扭称扭过的距离,可以达到1/4mm的精度。
根据卡文迪许的实验数据,当时计算出来的万有引力常数是6.74×10-11m3·kg-1·s-2,即使跟用现代手段测量的结果比起来,也可以说是非常精确了,只有1%的误差。
18世纪末的欧洲,英国还没有完全进入工业时代,实验仪器的精密度并不高。但是科学家们通过精心的设计,已经能够做出一些令人惊叹的测量,是非常了不起的!
第四节 天体运动的真实轨迹
了解了万有引力定律之后,理论上我们能计算出天体所有可能的轨道。但是在现实中,天体的运动轨迹真的是精确的椭圆吗?其实现实世界并没有那么完美。
椭圆进动(precession)
开普勒三定律首先推翻了天体运动是完美的圆的猜想。从古希腊时期开始,虽然没有明确的证据,但先哲们普遍认为天体的运行轨道是圆形,并且认为地球是宇宙的中心,所有天体都围绕地球转,这就是著名的地心说。
后来哥白尼(Nicolaus Copernicus)提出了日心说,直到开普勒三定律,才彻底否定了地心说,也否定了天体运动的轨道是圆形的。开普勒三定律在一定程度上支持了哥白尼的日心说,它告诉我们,太阳系里的行星都围绕太阳运动。
一般来说,天体的运动轨迹是椭圆形,但圆周运动也并不是完全不可能,因为可以把圆看成一个特殊的椭圆。当椭圆的两个焦点重合到一起,长轴和短轴一样长的时候,椭圆自然就演化成为一个圆了。
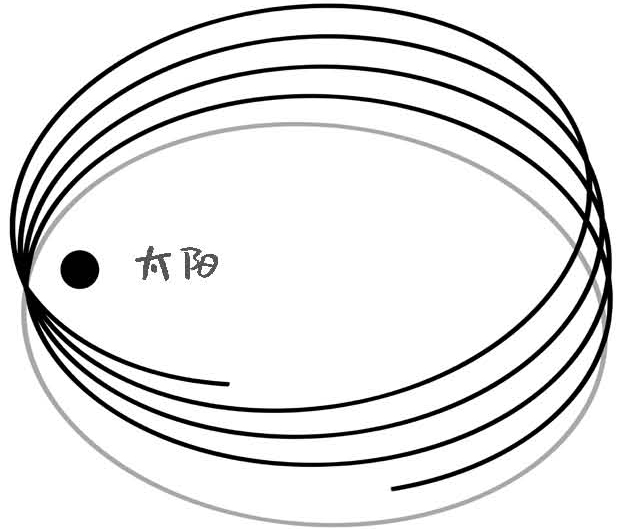
图6-9 椭圆进动轨迹
只不过正圆轨道的要求十分苛刻。在给定距离的条件下,运动速度的大小和方向必须十分精确地满足圆周运动的要求,才能形成一个正圆。所以真实的天体运动不太可能出现精确的圆形轨道,比如,地球围绕太阳运动的轨迹就是一个接近圆的椭圆。
那真实的天体运动是标准的椭圆吗?事实也并非如此。比如我们去计算地球公转轨道的时候,只考虑了太阳和地球两个天体。
但是别忘了,除了地球以外,太阳系还有七大行星和数量众多的其他天体,甚至是宇宙中的尘埃、小陨石,都会对地球有引力作用。只不过由于它们的质量跟太阳比起来都太小了,它们只在一个微小的程度上干扰,并不会显著地影响地球的公转轨道。
当地球花了一年时间转了一圈之后,集各种作用力于一体,它几乎不太可能精确地回到一年前出发的位置,而且公转速度的方向也几乎不太可能与一年前完全一致。
所以一个行星的真实运行轨迹,不会是一个封闭的椭圆:它大致以一个椭圆的形态转了一圈之后,会来到一个新的出发点,这个出发点与原来的出发点距离并不太远。在下一个公转周期里,它依然会以一个近似椭圆的形状转一圈,再来到一个新的出发点。
我们可以说天体的真实运动轨迹是一个进动的椭圆:一方面,天体沿着轨道运动;而另一方面,椭圆轨道整体也在行进,轨道本身也在围绕太阳转动。久而久之,天体运动的总轨迹就会变成像花瓣一样的形状。
除此之外,我们还会习惯性地认为小的天体绕着大的天体转,这样的描述也并不十分准确。因为万有引力的作用是相互的,地球在受到太阳引力作用的同时,太阳也受到地球的引力。
所以,准确的说法是太阳和地球共同围绕着二者的质心(center ofmass)运动。只不过由于太阳的质量比地球大太多,二者的质心落在了太阳内部。
彗星轨道
到此,我们可以对天体运动做一个完整的描述:天体运动是围绕着整个系统(包括该系统内的所有星体)的质心做椭圆进动。
在各种各样的椭圆轨道中,既有地球轨道这样比较圆的轨道,也有彗星轨道那样非常扁的轨道。彗星之所以很多年才出现一次,恰恰是因为它的轨道非常狭长。只有在运动到离太阳很近的位置时,才会被地球上的人看到。
图6-10 天体运行轨迹
轨道共振(orbital resonance)
进动的椭圆是对单个天体的运动轨迹所进行的描述,那么不同天体的轨道之间有没有什么关联呢?答案是有的,因为行星和行星之间也存在引力作用。
我们在太阳系中观测到了一种很特别的现象,就是围绕同一天体运动的若干天体,它们的公转周期会形成整数比。这种现象,叫作轨道共振。比如木星的三颗卫星[木卫一(Io)、木卫二(Europa)、木卫三(Ganymede)],它们围绕木星公转的周期比是1∶2∶4;而土星的两颗卫星土卫七(Hyperion)和土卫六(Titan),它们围绕土星的公转周期比是3∶4;海王星和冥王星围绕太阳公转的周期比是2∶3。
为什么是这样呢?
从物理层面上看,太阳系已经形成了几十亿年,在这几十亿年中,太阳系需要一个稳定的内部环境,即让系统处于一个周而复始、循环运动的状态。也就是说,经过一段时间(不管经过的整个时间长短如何)后,太阳系都会回到相对接近上一个周期的初始状态。
比如海王星和冥王星的公转周期之比是2∶3。如果把它们看成一个系统,这个系统要稳定,就必然会出现每经过一段时间,这两颗行星都要回到上一个周期出发时的状态。也就是说,要让这个系统复位。
所以,这两颗行星的公转周期之比,必然是一个有理数,可以写成几分之几的形式,因为只有这样,两颗行星的公转周期才会有一个最小公倍数。
以海王星公转周期的1/2作为一个时间单位,冥王星的公转周期就是3个时间单位,那么只要过6个时间单位,海王星和冥王星就可以回到最初的位置,再重复进行下一轮的运动。
如果两颗行星的公转周期之比是无理数,也就是无限不循环小数,那它们的周期永远无法找到一个最小公倍数。无论过了多长时间,它们也转不回初始状态,也就无法保证运动轨道的持续稳定。
如此看来,牛顿的万有引力真是太美妙了,它几乎能解释太阳系里一切天体的运动。但是在更大尺度上,万有引力定律真的是万能的吗?
爱因斯坦的出现,打破了牛顿理论那牢不可破的地位,让万有引力定律受到了巨大的挑战。爱因斯坦的时空观完全刷新了人们对于引力的认知。
