狭义相对论中的悖论
狭义相对论从刚发表的时候开始,就受到了学术界的诸多拷问,因为狭义相对论的结论对当时物理学界来说过于反常识,物理学家们也针对狭义相对论提出了许多问题,这其中有几个特别著名的悖论,这些悖论指出了狭义相对论中不完备的地方,由此发现,相对论终将被扩展为广义相对论。
第一节 梯子悖论(ladder paradox):相对论会颠倒因果吗
梯子悖论,揭示了相对论如何看待同时性(simultaneity)和因果律(law of causation)的问题。
什么是梯子悖论
原版的梯子悖论是用一架梯子和一栋房子来举例的。
为了便于理解,我们还是用爱因斯坦、普朗克和一列火车来说明。假设现在有一列火车,以接近光速的速度运动,正准备钻过一条隧道。火车上坐着爱因斯坦,隧道附近有一个相对于地面静止的观察者普朗克。梯子悖论我们给它改名叫“火车悖论”。
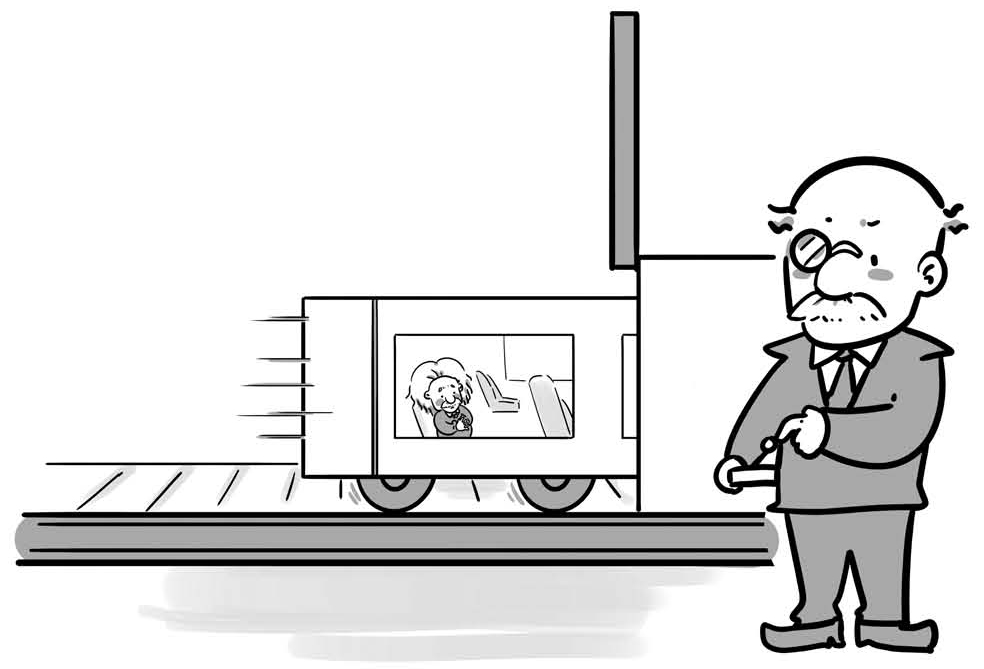
图2-1 爱因斯坦和普朗克的隧道游戏
先假设这列火车静止的时候,长度比隧道略长。火车运动起来之后,由于它的运动速度很快,地面上的普朗克看火车就会出现尺缩效应。我们假设,火车的运动速度刚好使得普朗克看到的火车缩短后的长度精准地等于隧道的长度。
隧道的出入口有两扇可开闭的门,用电子开关控制,开关掌握在普朗克手里。当火车进入隧道,运动到车头跟隧道的出口对齐,且车尾跟隧道的入口对齐时,普朗克会按下开关,让两扇门同时关上。但为了不让火车撞到门上,他关门之后马上再打开,让火车顺利通过。
那么对于普朗克来说,有这样一个瞬间,整列火车都被装在了隧道里。但当我们切换到爱因斯坦的视角来看这个问题时,就出现了矛盾。
对于爱因斯坦来说,火车是不动的,反而是隧道相对于自己迎面而来。所以在爱因斯坦看来,隧道的长度会缩短,比火车的长度还要短。也就是,根本不可能出现普朗克按下开关以后,整列火车被装在隧道的情况。因为隧道比火车短,一个短的隧道不可能装住一列长的火车。
但火车究竟有没有被隧道装在里面,这是一个客观事实。怎么会出现两个不同的观察者对同一个客观事件有不同的答案呢?这就引出了相对论如何看待同时性的问题。
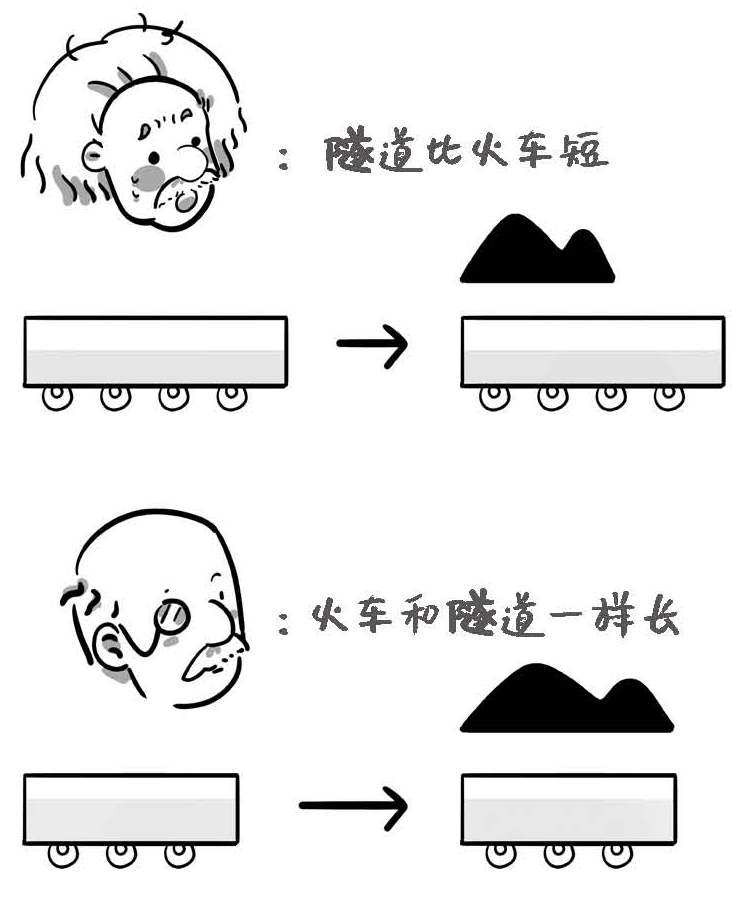
图2-2 爱因斯坦和普朗克的不同视角
什么是“同时”?
那要如何解释刚才的悖论呢?火车到底有没有被装在隧道里呢?
其实这取决于我们怎样定义一个事件。首先来检验一下对于火车被装在隧道里这个状态的描述。火车有没有被装在隧道里?其实指的是有没有那么一瞬间,整列火车全部进入隧道,并且隧道的出口和入口同时处于关闭状态。
这里的关键词是“同时”。火车是否被装在隧道里这件事情的本质,在于两扇门是不是同时处在关闭状态。对于普朗克来说,只要有那么一瞬间,整列火车全部进入隧道,并且隧道的出口和入口同时处于关闭状态,火车被装在隧道里这个事实就成立了。
但是对于爱因斯坦来说,火车全部进入隧道的情况不会发生,因为隧道的长度比火车还短。
但是如果普朗克真的让两扇门都关闭,爱因斯坦会看到什么呢?爱因斯坦会看到隧道的前门先关闭,然后马上打开,车头顺利通过隧道出口。等车尾通过隧道入口时,入口处的门才关闭。也就是说在普朗克看来两件同时发生的事,在爱因斯坦看来不是同时发生的。所以,只要把对于事件的定义拆解清楚,就不会发生具体事实的矛盾。
火车有没有被装在隧道里,这是人为定义的概念,不是物理的语言,所以要把这个定义拆解成物理的语言后,才能分析。
如何颠倒因果?
从上面的分析可以看出,在普朗克看来同时发生的事,在爱因斯坦看来并不是同时发生的。也就是说,在相对论里事件发生的先后次序,在不同的参考系里可能是不一样的。
在此基础上不妨大胆猜测一下:在一个参考系看来有先后顺序的两件事,在另外一个参考系里,它们的发生次序有可能是颠倒的。
还是用火车钻隧道的例子就可以证明这一点。这一次,我们让爱因斯坦的火车运动得再快一些,快到尺缩效应下的火车长度比隧道还要短一些。由于隧道两个口的门,关闭的规律是,入口处的感应器检测到车尾通过就关门,出口处的感应器则是检测到车头通过就立刻关闭,这样的话,在普朗克看来,车头还没有到隧道出口的时候,车尾就已经进入了隧道入口。隧道入口的门先关闭,出口的门后关闭。
但是在爱因斯坦看来,车速更快的话,说明隧道经历了尺缩,比火车短了更多,一定是隧道出口的门先关闭,入口的门后关闭,否则就会出现火车被隧道入口的门拦腰截断的情况,因为在爱因斯坦看来,隧道比火车还要短,车头到出口的时候,车尾还没有进入隧道。
所以对于哪扇门先关闭这件事,普朗克和爱因斯坦看到的结果必然是不同的。这就证明了在相对论中,事件发生的先后次序是可以颠倒的。
同时性的相对性(relativity ofsimultaneity)自然而然会引出一个最基本的问题:在相对论里,因果律可以颠倒吗?
第一章第一节中,我们就提到手枪和子弹的思维实验。从逻辑上来说,开枪这件事,必定是手先扣动扳机,子弹才能从枪口飞出,因果律必须要成立。
但是从火车钻隧道这个思维实验来看,似乎事件的先后次序又可以颠倒,这要如何解释呢?这里就引出了相对论里因果关系是否可以颠倒的问题。或者说,判断两件事是否可能存在因果关系的依据是什么?
在某一参考系看来,两个事件的发生必定对应两组四维的时空坐标,包括一个时间坐标和三个空间坐标。这两个事件发生的空间坐标的差异,也就是它们之间的距离,除以它们在这个参考系中发生的时间差,会得出一个速度。
判断因果关系的依据是这样的:在某个参考系中,如果这个速度大于光速的话,那么在另一个参考系看来,这两件事发生的先后次序就可能颠倒。换句话说,它们之间没有因果关系。
要如何理解两个事件之间的因果关系呢?就是一件事的发生是由另一件事导致的。
可以想象一下这个过程:第一个事件发生了,它会导致第二个事件的发生。那么第二个事件在发生前,一定要“知道”第一件事发生了。那么知道的过程就需要信息的传递。
然而信息的传递速度最快就是光速。也就是说,第二个事件得知第一个事件的发生有一个时间差,这个时间差最快就是两个事件发生的空间距离除以光速,因为充当信息传递最快的角色是光,或说电磁波。
所以,如果我们发现两件事情发生的时间差乘以光速得到的距离,小于它们之间的空间距离的话,就可以断定这两件事情没有因果关系。因为它们的时空间隔过大,导致第一个事件的发生不可能被第二个事件知晓,这两件事一定是相互独立的。
比如说在未来世界,人类文明已经扩展到全宇宙。在某个星球上发生了一桩命案,那么宇宙侦探来查案的时候,他要先调查一下死亡时间,知道命案是什么时候发生的。然后用现在的时间和死亡时间的间隔乘以光速,得出一个距离。
最后他就可以以这个命案发生的地点为球心,以刚才算出的距离为半径,在空间中画一个球。凡是现在在这个球以外的人,都不可能是凶手。因为在这个范围以外的事件,都跟命案没有因果关系。
这就是相对论告诉我们如何判断因果。反过来说,任何两件有因果关系的事,它们发生的空间距离除以时间差得到的速度,必定要小于或者等于光速,这样它们才有存在因果关系的可能。
而这样的两件事,在任何参考系看来,它们发生的次序都不可能颠倒。所以在相对论中,既定的因果关系是不会被打破的。
第二节 刚体悖论:狭义相对论对材料性质的影响
自从光速不可被超越的结论被提出后,科学家们设计了很多思维实验,试图证明光速存在被超越的可能。
超光速思维实验
假设孙悟空站在地面上,命令他那根金箍棒伸得很长很长,一直捅到月球(moon)上,并事先跟月亮上的嫦娥约定好:如果看到金箍棒动了,就放一束烟花。之后孙悟空在地球这一端向上推动金箍棒。如果金箍棒是一个绝对坚硬的物体,另一端的嫦娥会立刻看到金箍棒动了一下。这样的话,孙悟空就以超过光速的速度给嫦娥传递了一个信息。
月球到地球的距离有38万千米,光信号发过去需要超过一秒钟的时间,而孙悟空用金箍棒却能完成信号的瞬间传递。
孙悟空利用金箍棒还有很多方法可以做到超光速。比如他可以命令金箍棒伸长到银河系的中心,然后用力地挥动金箍棒。这样金箍棒的尖端就以孙悟空为圆心,以自身的长度为半径在宇宙中做圆周运动。而物体做圆周运动的速度等于半径乘以角速度,因此只要金箍棒足够长,孙悟空不需要挥舞得很快,金箍棒尖端的速度也可以轻松超过光速。
上面这两个案例,错就错在都假设金箍棒是刚体(rigid body)。
刚体就是完全没有弹性的物体。在现实世界中,一个物体不管多硬,只要有外力施加上去,都会发生形变。只不过硬度大的物体,在受到同样大小的外力的情况下,形变要比硬度小的物体小。
在弹性力学中,对物体施加的单位面积的外力叫应力(stress),单位体积物体大小的变化相对于没有外力时候的大小比例叫应变(strain)。应力除以应变,叫作杨氏模量(Young'smodulus)。杨氏模量越大,物体的硬度就越大,所以刚体就是杨氏模量无穷大的物体。
然而刚体是不存在的。因为万事万物都由原子构成,当给一个物体施加外力的时候,其实是第一排原子先发生运动,再推动下一排原子运动。而这两排原子之间是有距离的,第一排原子把运动传递给下一排原子就需要一定的时间。
所以即便第一排原子被推动得再快,这种运动信息传播的速度也不会超光速。孙悟空在地球上推动金箍棒,金箍棒的反应是先被压缩,然后再把这种压缩的趋势传递到月球上。这个传递速度并非光速,而是等于金箍棒内的声速,因为金箍棒被推动本质上是一种机械运动,机械运动在固体中的传播速度就是声速。
再看梯子悖论
了解了什么是刚体,我们再来看看火车悖论(梯子悖论)还能产生哪些有趣的现象。
还是假设爱因斯坦坐着高速运动的火车进入了隧道,普朗克操控隧道前后两扇门关闭。这次普朗克就不把门打开了,真的把这列火车装在隧道里。那么下一秒钟,火车就会撞到隧道出口的门上。
我们假设门是坚硬无比的,火车冲不出去,这样的话,火车就会被迫停下来。那么在普朗克看来,停下来的火车就被限制在了隧道里。但是由于火车停下来了,尺缩效应就没有了,火车要恢复原来的长度。而这个时候隧道的前后门已经关上了,所以火车就必须要经历一个被压缩的过程。
但是爱因斯坦会看到更奇特的现象。
首先爱因斯坦肯定会看到火车撞到前门的事件,但是根据同时性的相对性,这个时候后门还没有关闭。按理说,火车被迫停了下来,尺缩效应也会跟着消失。而火车本来就比隧道长,所以,不会发生整个被隧道装住的情况。
但是火车进入隧道被装住又是一个客观事实,普朗克明明做到了,还让火车经受了非常严重的挤压。这又是怎么回事呢?
答案是这样的:当火车头跟前门相撞的时候,车头感受到冲击力停了下来。但是这个时候车尾不会立刻停下来,因为车头已经停了这件事的信息,至少要以光速传递给车尾才行。所以在车头刚刚经历撞击的时候,车尾还没有反应过来,而是在惯性作用下继续向前运动。
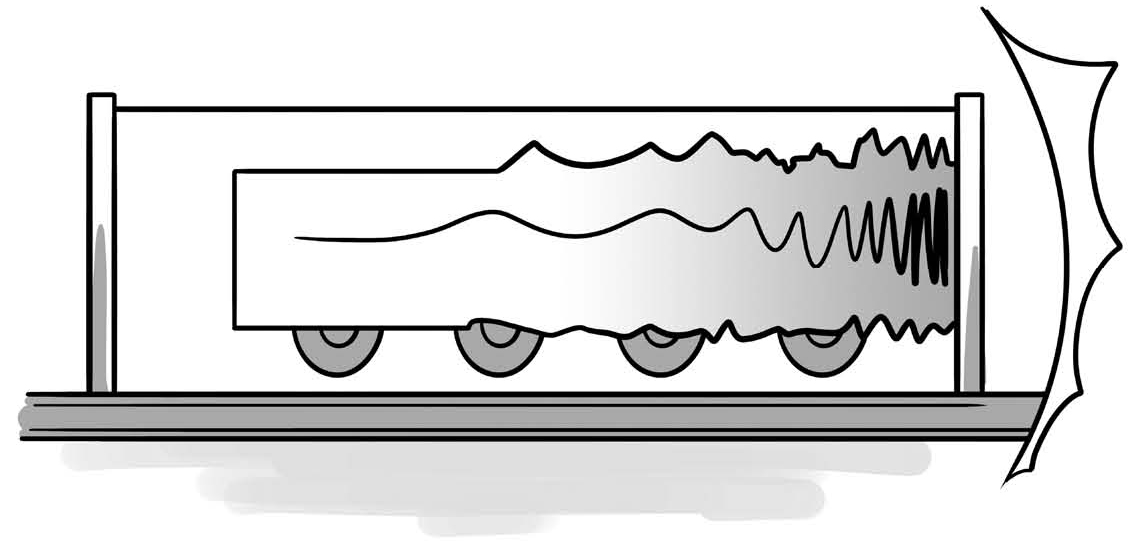
图2-3 机械波在火车内传播
按照物体的材料属性,车头已经停下来这个信息要什么时候能够传递到车尾,应该是由材料的弹性决定的。材料经历形变的信息在材料内的传播,叫作材料内的机械波,此信息传递速度应当是材料内的声速。
通常,杨氏模量越大的物体,它传递机械波的速度也更高,比如一根紧致的弹簧振动起来,就比一根同样大小的松的弹簧频率更高。所以车头停下来的信息传递到车尾的速度,是由火车的材料属性决定的。基本上火车的材料越硬,就会越快停下来。
但从另一个角度来看,情况就不是这样了。对于地面上的普朗克来说,火车什么时候完整地进入隧道是确定的。在普朗克看来,前门和后门关闭的时间是同时的,通过狭义相对论中的“洛伦兹变换”,我们可以精确地知道切换到爱因斯坦的视角,前门和后门关闭的时间差,这个时间差是唯一确定的。
也就是说,无论火车是用什么材料做的,它必须在确定的时间进入隧道。这样的话,火车的弹性似乎就跟材料没有什么必然联系了。
这里就又出现了矛盾,在真实世界里,一个物体的弹性不可能跟它的材料无关。我们可以用不同的材料来造这列火车,比如用钢铁和棉花糖,看到的效果肯定是不一样的。
然而根据狭义相对论的计算,无论怎么改变火车的材料,似乎都不影响它的弹性。那么要如何解决这个悖论呢?
在学习狭义相对论的时候,不得不时刻强调它的使用边界。狭义相对论研究的对象太过理想,只适用于匀速直线运动的物体。一旦涉及加速、减速的问题,比如爱因斯坦乘坐的火车突然停下来,就已经不在狭义相对论的讨论范围内了。
因为有了加速度,上面分析的悖论就成了一个狭义相对论解决不了的问题。
第三节 埃伦费斯特悖论(Ehrenfest paradox):时空的扭曲
埃伦费斯特悖论是埃伦费斯特针对狭义相对论提出的一个思维实验。为了解决悖论,你会发现狭义相对论真的是不够用了,必须要引入广义相对论的基本假设才能解释。
这个悖论也大大启发了爱因斯坦去思考广义相对论的问题。
埃伦费斯特悖论
首先来复习一下最基本的几何知识。中学里都学过如何计算一个圆的周长,圆的周长等于圆的半径乘以2π,其中π是圆周率,是个无理数(irrational number),约等于3.1415926。
假设有一个圆盘,半径用字母r来表示。首先让圆盘高速旋转,速度快到什么程度呢?快到它边缘的旋转速度非常接近光速。
这个时候,假设爱因斯坦站在圆盘的中心,因为圆盘的中心并没有旋转,所以爱因斯坦是静止的。现在爱因斯坦要去观察两个物理量:一个是爱因斯坦正前方看到的圆盘边缘的一小段圆弧的长度,另一个是连接爱因斯坦和这一小段圆弧的半径。
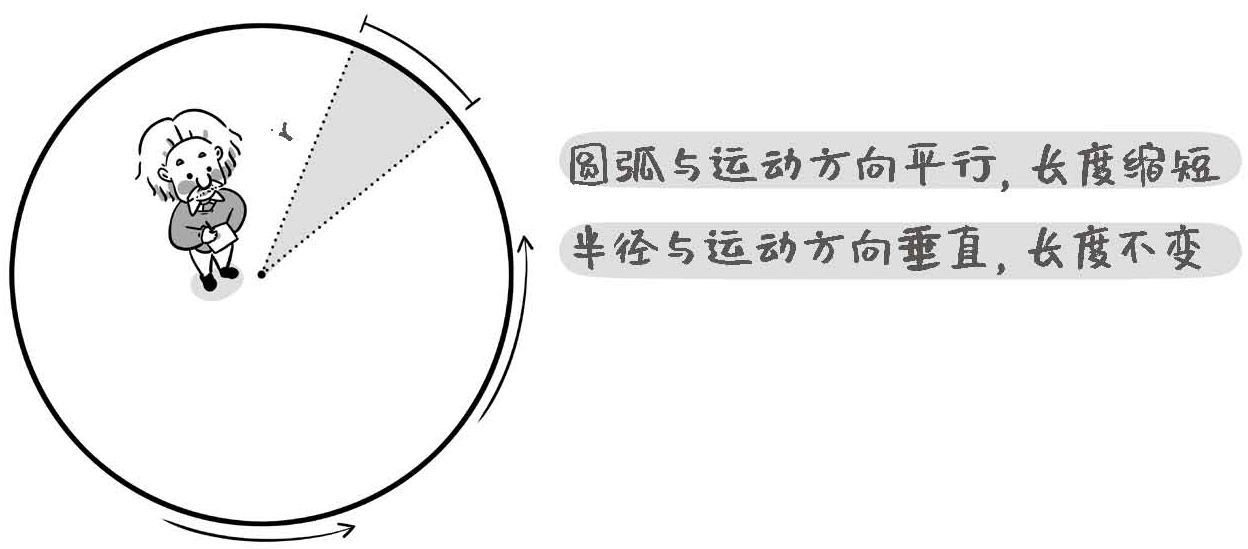
图2-4 爱因斯坦观测圆弧长度和圆盘半径
根据之前介绍过的尺缩效应,由于这一小段圆弧的长度与圆盘边缘的旋转方向是一致的,爱因斯坦看到圆弧的长度会缩短。但是这条半径与圆盘边缘转动的方向是垂直的,所以尺缩效应不会作用在半径上,半径的长度不会缩短。
要知道,圆的周长是由一段段圆弧组成的,如果每一小段圆弧的长度都缩短了,圆整体的周长也会跟着缩短。那么问题来了,圆的周长是2π乘以半径,换句话说,周长和半径成正比。但是很明显,在这种情况下,圆的半径没有变,周长却变短了,于是就出现了矛盾。
圆盘的周长到底变还是不变?这就是埃伦费斯特悖论的核心。
欧几里得几何(Euclidean geometry)的破溃
这个悖论要如何解释呢?跟上一节的结论类似:在这个悖论的情况下,狭义相对论并不适用。
一定要反复强调,狭义相对论的适用情况是匀速直线运动,是没有加速度的情况。但是这个悖论里的圆周运动并不是匀速直线运动,圆盘在转圈时有向心加速度(centripetal acceleration)。
如果我们看圆盘边缘的每一个点,它们确实在以固定的速率绕圆心转动。但是在转动的过程中,虽然速度大小是不变的,方向却一直在改变,所以圆盘上的点并不是在做匀速直线运动。
既然在这个悖论里狭义相对论不适用,就要用广义相对论来解决问题。广义相对论的一个重要观点是:时空是可以发生扭曲的。
先来说说什么叫平坦的时空(flatspacetime)。我们上中学都学过几何,中学学的几何是欧几里得几何。欧几里得几何里有一个基本假设,或者说公理,就是两条平行线永不相交,或者说两条平行线只在无穷远处相交。然而这个公理只在平坦的平面上才成立。如果是在一个不平坦的平面,或者说一个曲面上,它就不成立了。
举个简单的例子,我们在一张平坦的纸上画一个正方形或者长方形,它的四个角都是直角,且两组对边分别平行。也就是说在一个平面上,如果用一条线把两条线连起来,并且这条线跟两条线的交角都是直角的话,就能判断出这两条线是平行线,它们永远不会相交。
但这个判断标准在曲面上就不成立了,比方说地球的表面。我们知道,地球上任意两条经线在南极和北极会汇聚到一点,但是在地球上的其他地方都不会相交。如果我们在两条经线中间找到一条纬线,这条纬线与这两条经线的交角一定都是90°。因此在一个球面上,只看局部关系的话,可以说这两条经线是平行的,但它们显然不是永远不相交的,而是会在南北两极汇聚。
这种研究曲面的几何,就不是欧几里得几何了,而是黎曼几何(Riemannian geometry)。黎曼(Riemann)是19世纪最伟大的数学家之一,广义相对论就是建立在黎曼几何的基础上的。
但是要知道,一个圆的周长等于2π乘以半径的结论,是在欧几里得几何里才成立的。在空间不平坦的情况下,欧几里得几何不成立。
这样我们就知道如何粗略地解释这个悖论了:首先由于整个圆盘并非在做匀速直线运动,所以狭义相对论不适用,要用到广义相对论;广义相对论的核心概念是扭曲的时空,时空扭曲(distortion ofspacetime)之后,就不能用欧几里得几何的结论去算圆的周长了。
因此,在这个悖论的设置中,圆的周长确实缩短了,但是圆周的半径并没有变化,这并不构成矛盾,只因为周长等于2π乘以半径是在欧几里得平坦空间的情况才成立,如果是满足非欧几何的空间,并没必要满足这个简单的几何关系。
第四节 双生子悖论:狭义相对论破溃了吗?
哥哥和弟弟谁更年轻?
狭义相对论中最著名的悖论,要数双生子悖论,也叫双生子佯谬(twin paradox),同样是一个思维实验。
假如有一对双胞胎兄弟,哥哥坐着一艘宇宙飞船,以接近光速的速度去太空里转了一圈,又回到地球上,而弟弟一直在地球上待着。问:飞船回来以后,兄弟俩谁的年纪更大一些?
根据钟慢效应,由于哥哥的运动速度非常快,所以在弟弟看来,哥哥的时间流逝速度非常慢。这样等哥哥回来后,弟弟经历的时间更长,所以哥哥反而比弟弟年轻,哥哥就变成了弟弟,弟弟变成了哥哥。
这样一个推论看似没有什么问题,但是这里面隐含着严重的逻辑矛盾。
虽然是哥哥坐着宇宙飞船去太空里转了一圈,但是在哥哥看来,何尝不是弟弟在地球上,地球相对于哥哥坐的宇宙飞船,也以接近光速的速度转了一圈。因为运动完全是相对的,无论是哥哥还是弟弟,都会觉得自己是不动的,是对方在运动。
所以对于哥哥来说,应该是弟弟的时间流逝速度更慢。当自己回到地球以后,哥哥应该更加年老,哥哥还是哥哥,弟弟还是弟弟。
相信你一定坐过高铁,不知道你有没有过这样的感受:当你坐在高铁上,车还没有开动,在你坐的高铁旁边还有另外一列高铁。如果你望向窗外,发现对面的高铁开动了,这个时候你很有可能会产生错觉,你无法判断到底是对面的高铁开了,还是自己坐的高铁开了。
因为运动是相对的,你只能判断对面的高铁相对于你运动了。至于到底是你所乘坐的高铁开动了,还是对面的高铁开动了,你是无法判断的,因为高铁是在太平稳了,这时你几乎无法通过触觉来判断自己的列车是否开动。
同理,在宇宙飞船的思维实验中,如果哥哥和弟弟不知道自己具体是在地球上还是在宇宙飞船上,只能看到对方的相对运动的话,就会产生钟慢效应的悖论。也就是对于哥哥来说,弟弟更年轻了,而对于弟弟来说,哥哥也更年轻了,那么究竟是谁更年轻了呢?
但是很显然,一件事不会有两个结果。真要做这么一个实验的话,最终要么是哥哥更年轻,要么是弟弟更年轻。如果折中一下,两个人的时间流逝速度还是一样的话,那钟慢效应的推论不就破溃了吗?
考虑加速过程
与前文的结论类似,狭义相对论的研究对象只能是做匀速直线运动的物体,不考虑有加速度的情况。加速度也属于广义相对论的讨论范畴(注:现代关于广义相对论与狭义相对论的界限问题,不同学术流派有不同观点,譬如有的流派认为可以把加速的情况吸收进入狭义相对论的理论体系当中,而广义相对论只处理存在引力的情况,这种做法从计算上来说确实存在先进之处,但是两种方法并无对错之分)。
如果真的分析一下这个思维实验,就会发现,我们在逻辑上有一个巨大的跳环。一开始,哥哥和弟弟都在地球上,两个人是相对静止的。之后哥哥坐上了宇宙飞船,宇宙飞船一路加速到接近光速,哥哥实实在在地经历了一个加速过程。
但是之前已经说了,狭义相对论只讨论匀速直线运动的情况,不考虑加速的情况,因此在分析这个问题的时候,不能只在狭义相对论的框架下来讨论,也必须要借助广义相对论。
其实仔细想一下就会发现,双生子悖论会遇到困难,是因为哥哥最终要回到地球跟弟弟见面。这一见面,就会有谁更年轻的问题。但是如果哥哥飞出去以后,一直不回地球的话,即便在哥哥看来,弟弟流逝的时间更慢,在弟弟看来,哥哥流逝的时间也更慢,这本身是没有矛盾的。
只要不存在最后哥哥回到地球与弟弟见面的环节,哥哥和弟弟各自的时间在自己看来都是正常的。而对于对方来说,只要没有验证的环节,狭义相对论就不会破溃。
来看一个具体的例子。假设哥哥的飞行速度快到刚好使得弟弟看哥哥时间流逝的速度是弟弟的十分之一,这个速度是非常接近光速的,大约是光速的99.5%。由于运动是相对的,哥哥看弟弟的时间流逝速度也应该是自己的十分之一。假设哥哥出发的时候,两个人都是20岁。
当弟弟看自己的时间过了一年的时候,他给哥哥发了一条信息,说:哥哥,我这里已经过了一年了,我现在21岁了。然而在哥哥看来,由于弟弟的时间过得非常慢,弟弟在发出这条信息的时候,哥哥自己已经过了10年了。并且对于哥哥来说,这十年间自己是以接近光速的速度在飞行的,所以弟弟发信息时,哥哥离地球的距离大概是10光年。而这条信息从发出到被哥哥接收到,又要花上10年左右。因为根据光速不变原理,这条信息要以光速跨越10光年的空间距离追上自己。所以当哥哥收到信息的时候,自己相较于从地球出发时已经过了20年了。

图2-5 哥哥比弟弟年轻?
哥哥收到信息后马上给弟弟回信,说:弟弟,我已经40岁了。其实这个时候哥哥可以推算出,弟弟应该是22岁。但是在弟弟看来,整个过程就不是这样了。由于弟弟发信息的时候自己只过了1年,所以哥哥离自己也只有约1光年远,信息只需要追1光年的距离。
但是在信息追赶哥哥的过程中,哥哥还在继续以略低于光速的速度远离。所以弟弟发出的信息虽然是光速,但是它要追上以略低于光速飞行的哥哥是要花非常久的时间的,因为哥哥的飞行速度是光速的99.5%,所以信息追上哥哥的相对速度只有0.5%的光速,这个相对速度要跨越1光年的相对距离,要花200年时间。等哥哥收到这条信息的时候,弟弟这里已经过了200年的时间了,与哥哥之间的距离也远远超过200光年。
还是根据光速不变原理,哥哥的回信在弟弟看来要以光速跨越这段距离,还需要经过很长时间,大约又是200年才能传到弟弟手中,而在回信中哥哥声称自己只有40岁,但弟弟接到哥哥信息时已约420岁了。
这样一来就没有矛盾了。无论是哥哥还是弟弟,收到对方的信息后再跟自己当时的时间进行比较,都会发现,从信息上来看,对方比自己年轻了。狭义相对论的钟慢效应对双方来说都是成立的。
到底谁更年轻?
上面的分析仍然是在狭义相对论的范围内讨论的。如果运用广义相对论,真的让哥哥返回地球跟弟弟见面,到底谁会更年轻呢?答案是哥哥,因为哥哥会经历速度改变的过程。
在广义相对论中,经历加速或减速的过程会使时间的流逝速度变慢。哥哥要想完成星际旅行,必须先加速,运动到最远处减速停下来,然后返航时再经历一次先加速后减速的过程。
根据广义相对论,哥哥完成这一系列动作,时间流逝是更慢的。关于应用广义相对论如何完满地解决双生子悖论问题,我将在“极重篇”给出具体解释。
通过本章中关于狭义相对论的若干个悖论我们可以看出,狭义相对论其实重新定义了许多传统观念中不清晰的概念,很多悖论是可以通过对概念的清晰界定解决的。但是更多地,我们从这些悖论中了解到了狭义相对论的局限性,毕竟它只讨论匀速直线运动的情况,更广泛的情况自然是要用到广义相对论才能解决的。
狭义相对论对于双生子悖论的解释*(星标表示非必读内容)
双生子悖论实际是一个非常著名的问题,关于双生子悖论的解释一直到20世纪50年代,也就是狭义相对论已经被研究得非常明晰的时代,还被再次热烈地讨论过。爱因斯坦本人最早对于双生子悖论的解释,就是前文提到的讨论加速过程并运用广义相对论等效重力的解释,但是其实即便不考虑加速过程,双生子悖论依然可以得到解释。
我们可以通过设计一个思维实验来进行论述。想象一个观察者A,他始终在地球上,观察者B乘坐宇宙飞船,在地球上进行加速,等加速度到一定程度飞出地球,在飞出的一刹那,B与A把手表对准。对准时间后,B便以匀速飞往外星,在外星上也有一个观察者C,C也在不断加速,等B到达外星的时候,C以跟B相同的速度大小飞向地球,并且在C飞出去的瞬间,C会跟B对时间,并把自己手表上的时间调成跟B相遇的时间,这样的话当C到达地球的瞬间(C并未减速,而是保持与B相同大小的速度掠过地球),C的手表上的时间就应该是排除加速过程,从地球到外星之间往返的时间。这样我们就得到了一个不考虑加速过程的双生子悖论的设置。
这样的设置就能很好地解释双生子悖论,双生子悖论的根本矛盾在于,哥哥的参考系和弟弟的参考系应当是完全对称的,双方看对方都是在相对于自己运动,这样的话,双方看对方都更年轻,最后不应当出现两个人年龄不同的“非对称”的结果。但是从上面的设置可以看出来,离开地球和返回地球,根本是两个完全不同的参考系,因为这两个参考系速度大小虽然相同,但是方向完全相反,因此地球上观察者A的参考系,与BC二者的参考系并非对称,最终结果是非对称的完全合理。如果真的代入数字,通过洛伦兹变换进行计算,就会发现,确实是出去飞了一趟的人,时间流逝速度更慢。通过参考系的非对称,就解释了双生子悖论。
