复杂系统
第一节 三体问题
世界是流变的,现实世界中物理系统的状态往往都是非稳态的。比如不同天气交替变化,气象系统就是非稳态的;涉及运动的情况,生活中的各种交通工具设计时都要考虑与流动的空气间的相互作用。空气的流动大多是非稳态的,我们必须要研究非稳态系统的规律,才能更好地解释世 界。
因为变化太多,非稳态系统通常很乱,乱其实就是熵值高。随着温度的变化,熵值会发生变化,所以,我们就将极乱的情况归到“极热篇”中一起讨论。研究极乱情况的科学领域,叫作复杂科学。
三体问题
先来看复杂系统最早的问题之一,也就是著名的三体问题。三体问题因为著名的科幻小说《三体》而变得广为人知。最早研究三体问题的是19世纪的法国大数学家庞加莱(Jules Henri Poincaré)。
三体问题的设置极其简单,当时人们已经清楚了天体之间的作用是万有引力。假设有三个质量相当的天体,天体之间两两存在万有引力。三体问题就是在已知天体相互作用规律的情况下,如何解出三个天体的运行轨迹。当然,如果拓展到四体、五体,这个问题的难度会更高。
这里要明确,所谓三体问题并非局限于三个天体之间两两以万有引力的形式相互作用,如果是其他更加复杂的相互作用形式,譬如说我们用广义相对论方程来描述三个天体的运动,都同样是复杂的。三体问题所聚焦的问题,其实是个数学问题。
什么是解析解(analyticalsolution)?
庞加莱很快发现,要把三体问题中天体运动所满足的方程式写出来非常容易,但这个方程完全没有办法用解析的方式进行求解。
三体问题方程式:
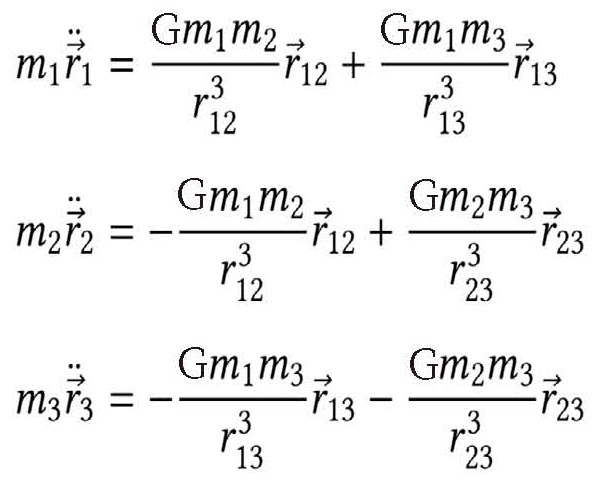
有解析解,就是指一个方程的解可以用函数形式清晰地表达出来。比如,一个一元二次方程的求根公式就是它的解析解。没有解析解的意思,就是一个方程不存在求根公式。比如一元二次、三次、四次方程都有求根公式,到五次方程及以上,就没有求根公式了。
什么是数值解(numericalsolution)?
如何理解什么叫作没有解析解?譬如超越方程(transcendental equation)就没有解析解。x2+sinx=0,就是一个超越方程。这种方程的特点是它的解在数轴上的分布非常散乱,没有办法用已知的函数统一表达。我们确实可以用计算机一个个试出来它的解大概有哪些,但这些解并不能对应于一个具体、已知函数的规律。
没有解析解代表一个方程过于复杂,导致没有已知规律可以描述它。对于这种方程,我们能够追求的最多就是数值解,也就是我们只能给出这些解在数值上等于多少。
通过三体问题中物体的运动方程,写出三个物体的坐标,如 x、y、z。其中,x的受力情况与x、y、z三个位置都有关,另外两个物体的受力情况也是如此。每个自变量都是另外两个自变量的函数,这三个方程是高度纠缠在一起的。
这种高度纠缠在一起的方程式非常复杂,虽然单个方程的形式看上去都很简单。一个三元方程组的标准解法是代入法,将三个方程联立,消掉两个未知数,最后剩下一个未知数。但是由于方程组相互纠缠,导致最后消掉未知数的方程形式特别复杂,因此没有解析解。
对于三体问题,我们似乎只能谋求数值解,用计算机代入数值去试出答案。
复杂系统对误差的敏感性
遗憾的是,从原理上我们也无法解出三体问题的数值解。这是因为三体问题对初始条件和误差过于敏感,导致方程解出来与正确答案相去甚远。如何理解呢?这就要说到数值解的基本方法。
对于一个只能谋求数值解的方程,求数值解时的基本方法,就是先猜,再比对,再修正,然后循环往复,直至逼近答案。比如面对一个方程,我们的办法是先猜一个数值解,然后看一下它能否使方程成立,当然,大概率是无法成立的;下一步,就是看看猜的这个数值距离让等式成立差多少。如果差数字2,我们就再猜下一个数字。将下一个猜的数字代入方程后,发现距离等式成立变为差3,就说明第二个数值猜的方向错了。这时可以换一个方向猜,猜完再代入,如果发现偏差缩小,就继续往刚才的方向上猜。每次猜完之后,都要代入方程去看差值是变大还是缩小。这样的过程循环往复,总能找出正确答案。
但是对于三体问题却做不到,为什么呢?正是因为对初始条件的敏感度。当我们去猜数值的时候,只要猜错就会产生误差。你以为可以猜第二个数值,但是当你去猜第二个数值、第三个数值……不断代入的过程中,会发现将每次猜的数值代入方程得出的误差值根本不能给你应该怎么去猜数值提供方向。也就是上面先猜后代入的过程给出的数值结果太敏感、太跳跃了。可能第一次猜了一个数值,误差是2,第二次猜了一个数值,误差是1,你觉得这个方向对了便继续往这个方向猜,但将第三个数值代入时,误差又变成20了,完全失去了做数值计算的方向,使数值解法根本无法得出正确答案。这就叫对初始条件和误差的敏感度,初始条件在这里就应该理解为误差。
可以想象一下,三个天体在时间等于0时被释放,在万有引力作用下开始运动。初始条件是我们清楚三个天体被释放时的具体位置,也知道它们被释放时的速度。初始条件敏感是指开始运动的位置和速度,只要稍稍有一点儿偏差,哪怕是极小的偏差,最终也会导致完全不同且毫无规律的运动轨迹。
做数值计算时的敏感性,会导致我们根本无法用猜数值的办法逼近正确答案。如果用计算机程序去模拟三体运动,你会发现它的运动规律是杂乱无章的。哪怕初始条件设定的一样,计算机模拟的运动轨迹也将与真实世界的三体运动完全不同,因为计算机的模拟总是有误差的。
三体问题的特殊解
这样一来,三体问题是不是完全无解了呢?三体问题其实在一些特殊情况下有特殊解。比如,我们把三个完全相同的天体组成一个正三角形,让它们围绕着三角形的中心以一定速度旋转,只要旋转的速度合适,确实可以形成一种三个天体匀速旋转的运动模式,或者三个天体连成一条直线,围绕中间的天体以一定角度旋转的运动模式。这些都是特殊三体系统的特殊运动模式。
再比如,三体中有两个天体特别轻,一个天体特别重。这种情况下稳定的运动模式则是两个小天体绕着一个大天体旋转。这也是为什么在太阳系这样稳定的恒星系中,恒星的质量要远大于其他天体的质量,这样才能让恒星的引力成为主导,让其他的天体围绕它旋转,否则太阳系不可能是稳定的。如果八大行星跟太阳的质量相当,那么太阳系的运动将极其混乱。
小说《三体》中所描绘的三体人所在的星系,就是因为有三个太阳,导致它们的天体运动极其不稳定,所以三体星没有稳定的气候,导致三体人不得不出去征服其他星球。
当然,三体问题只代表了一个大学科中的一个典型问题。三体问题尚且不可解,可见这个学科是非常庞大复杂的,这就是复杂科学。
第二节 湍流问题(turbulence problem)
三体问题其实只是复杂科学中最典型的问题之一,现实生活中的复杂科学问题比比皆是,甚至可以说复杂系统比简单系统多得多。
流体动力学(fluid dynamics)
有一门古老的学科叫流体动力学,它研究的是气体、液体在流动状态下的物理学规律。流体力学的应用非常广泛,比如航空航天,本质上就是在深入钻研空气的流动;造船技术则是研究水的流动。空气、水在流动中的运动规律,在微观层面上是可以用牛顿定律描述的,但不可能每个分子都可以用牛顿定律去描述。尽管它的运动从原理上来说我们很早就清楚,但里面一些悬而未决的问题却已困扰科学家几百年了。
流体力学的研究方法
流体力学的标准研究方法,是用流速去描述流体中每个位置的运动情况。我们并不追踪每个流体分子的运动,而是把流体当作一个整体进行研究,关注流体会通过的区域内,每个具体位置的流体流速是什么样的。在流体流动过程中,虽然每个位置流过的流体分子一直在换,但这里我们不关心每个具体的分子,只关心分子的“流”,也就是区域内每个位置流体的流速。
我们在“极快篇”的第三章《人类提速之路》中提到过伯努利定理,即流速越快,压强越小,伯努利方程给出了流速与压强的关系。只要了解了每个位置流体的流速,就能够了解每个区域内的压强。也就是说,置身于流体中的物体的受力情况,可以根据流体的流速计算出来。
NS 方程
结合伯努利定理和牛顿定律,原则上,只要解出流体的速度分布的方程——Navier-Stokes方程(英文缩写为NS方程),流体的行为就能被彻底理解。
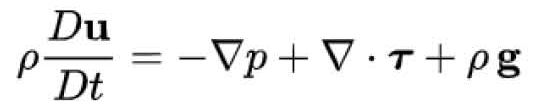
但到目前为止,NS 方程也没有被彻底解决,只有一些特殊情况下的NS方程是有解析解的。在大部分情况下,NS方程甚至连数值解都没有。为什么呢?这其实跟三体问题类似,因为NS方程里有一个黏性阻力项,数学上体现为自变量的平方项,这在数学上叫非线性(nonlinear)。但凡速度有点偏差,就会被这些非线性的项无限制放大。也就是一个非常微小的扰动,就会导致最终的结果南辕北辙。
著名的法国数学家达朗贝尔(Jean le Rond d'Alembert),曾经通过研究流体力学得出了著名的达朗贝尔佯谬(D'Alembert's paradox)。达朗贝尔佯谬是说,如果流体是不可压缩且无黏性阻力(viscosity)的话,则流体对于置身其中的物体的拖拽力为零,这意味着一艘船在水中行驶的话将不会受到任何阻力,简直就跟超流体一样,这是与事实完全不相符的,因此研究流体必须要把流体的黏性阻力,甚至密度随压力的变化考虑进去。
NS方程是数学界的“七大千禧问题”之一。美国的克雷数学研究所(Claymathematics Institute,英文缩写为CMI)在2000年列举了七个数学问题,并对每个问题悬赏100万美元,称这七个问题是千年难题,NS方程的解就在其中。这就引出了流体力学当中一个至今都无法彻底解决的物理现象——湍流。
什么是湍流?
湍流,也叫乱流,湍流的现象很常见。比如坐飞机时导致飞机颠簸的气流,就是湍流。国外航班的广播里直接说的就是“turbulence”。
什么是湍流呢?其实翻译为乱流更为贴切。湍流就是一种毫无规律的空气流动。由于毫无规律、变化剧烈,所以坐飞机时感受到的是颠簸。湍流,就是NS方程非线性的体现。
历史上很多前沿的物理学家和数学家都尝试去解过湍流问题,可见其难度之高。比如海森堡的博士论文就企图解湍流的问题,可他解了几年发现完全无法解出来,只给出了一些特殊情况,可见湍流问题有多难。

图17-1 湍流的形态
湍流中是有一些相对来说比较稳定的特殊情况,比如空气和水会以转圈的形式开始运动,形成流体的涡旋。但是这都只是NS方程的特殊解,并非全貌。
雷诺数(Reynolds number)
湍流问题目前还无法精确求解,也就是说无法解出湍流情况下,一块区域内每一个位置的流速按什么规律变化。即便无法精确求解,也可以考虑其他情况。比如,可以解释湍流为什么会形成,以及在什么情况下会形成。
于是就有了一个概念,叫雷诺数。首先,一般的流体之间有黏性阻力,也就是流体之间有相互作用。如果描述流体的模型中没有黏性阻力,就不会出现湍流。
在没有黏性阻力的情况下,流体的行为是非常顺滑的。也就是说,一个区域内各个位置流体速度虽然不同,但不同流速流体之间的相互作用只体现在流体的压强上,而压强的方向垂直于流体流速方向,所以并不会影响流体的速度。但是一旦有黏性阻力,流体的运动就会受到黏性阻力的影响。所以,NS方程的一般形式里都是有黏性阻力的,这也更符合实际的流体情况,达朗贝尔佯谬告诉我们,实际流体必须考虑黏性阻力。
结合一下生活经验,如果你坐过快船,可以观察一下,当船在刚开始启动速度还比较低的情况下,在水里激起的水波是比较规律的,但是船的速度起来之后,它的周围就会有比较大的浪花。这些浪花就是一种湍流行为。
雷诺数描述的就是这个现象,雷诺数就是流体被喷出时的动能与流体受到的黏性阻力的比值。这个数字大到一定数值,就会出现湍流。这个过程从物理上可以这样理解:因为黏性阻力跟速度成正比,能量跟速度的平方成正比。当速度很慢的时候,速度的平方没有速度的一次方大,所以黏性阻力占主导地位,能够限制流体的运动。随着速度越来越快,速度的平方就会越大,整个流体会对扰动相当敏感,系统就会迅速进入混乱、不可预测状态。进入混乱状态以后,具体的行为就变得无法描述了。
雷诺数看似粗浅,对于流体系统来说却是一个重要的进步。要知道湍流的产生对于飞行器来说,是一个重大的阻力来源。如果有办法改变飞行器的形状以及飞行模式,让飞行器在尽量高的速度下才超越雷诺数的上限,这对于飞行器的提速将有重大帮助。
湍流的问题,只是一类复杂系统的问题。这样的问题还有很多,它们可以被归为同一种类型的系统,叫作混沌系统。
第三节 混沌系统与蝴蝶效应
蝴蝶效应
我相信你一定听说过蝴蝶效应,它是由一名叫洛伦兹(Edward Lorentz)的气象学家提出的。这个洛伦兹跟我们电磁学里的那个洛伦兹力的洛伦兹不是一个人,洛伦兹只是一个很普遍的姓氏。蝴蝶效应的原话是:“一只南美洲亚马孙河流域热带雨林中的蝴蝶,偶尔扇动几下翅膀,两周后可能在美国得克萨斯引起一场海啸。”

图17-2 蝴蝶效应
蝴蝶效应并不是说这只蝴蝶扇了翅膀直接导致了得克萨斯的海啸。天气系统是一个极其复杂的系统,初始条件的不同会导致完全不同的结果,这才是蝴蝶效应的真实意思。
确定性系统的非确定性
这类问题引出的系统,叫作混沌系统。这类系统对初始条件极其敏感,它表现出一种巨大的随机性。注意,此处的随机性跟我们在“极小篇”里提到的量子力学的不确定性原理所对应的真随机性不是一回事。量子力学里的随机性对应的系统本来就是不确定的系统,但是混沌系统是完全确定的系统(deterministicsystem),比如天气系统。我们可以认为天气系统里每个空气分子的运动形态,都可以被确定。
但由于系统对于初始条件、误差以及扰动的敏感性,会导致这个系统在实际操作中变得完全无法预测。这里的无法预测应当被理解为在目前的数学体系框架下的无法预测,但系统的规律是确定的。每一个粒子的运动规律,都唯一被牛顿定律牢牢固定(此处不考虑粒子的量子属性)。任何单个粒子与其他粒子的相互作用,发生碰撞前后的规律都是确定的。但整个系统特别敏感,导致从方法论上无法解出它的变化规律。
混沌系统是一个完全确定的系统,但是初始条件的极小偏差,并不意味着结果的偏差也是极小的。
从数学上描述混沌系统的方程式通常有一个特点,叫作非线性,也就是在方程式里,会出现速度的平方项、位置的平方项这样的数学表达。如果存在一个误差,由于有平方项,这个误差就会在计算的过程中呈指数规律增大,最终会被放大到极其远离正确答案的路径上去。
系统方程的非线性,是导致系统混沌性的一个根源。
混沌系统的研究方法
从数学上看,当面对这样的混沌系统时,我们似乎是无能为力了。这种情况在研究量子力学时也碰到过,由于不确定性原理,我们发现已经无法用原子中电子的具体轨道来描述电子的运动了。于是人们发明了概率波来描述粒子的运动,抛弃追求电子轨迹的执念,寻找一种新的描述语言来解决问题。科学家们甚至总结出了不确定性原理,它从原理上告诉我们,电子不存在轨迹,因为位置和速度无法同时被确定。同样,面对混沌系统,我们是不是也应该抛弃计算系统随时间变化的具体规律,转而去寻找一些混沌系统的其他规律呢?
答案是肯定的。对于混沌系统,我们可以去寻找它们的特殊解和稳定解。
先来说说什么是特殊解。我们在三体问题里就提到过一些特殊解。三个质量相同的天体,分别占据正三角形的三个点,以一定速度围绕中心转动,这种解必然是存在的,这就是个特殊解;三个天体连成一条直线围绕中心天体旋转,也是一个特殊解;如果两个天体质量很小,一个天体质量很大,两个天体一近一远围绕大天体运动,就好像太阳系的行星绕太阳运动一样,这种解也肯定是存在的。这三个解,都是三体问题的特殊解。
在混沌系统中,系统随时间的变化规律杂乱无章,特殊解对应的是在杂乱无章的运动中,有规律的那些解。它们通常是周期性、有特征的。
但是特殊解未必都是稳定解,还是拿三体问题的三种特殊解来看,三个天体连成直线一起运转这个解明显不稳定。为什么?因为只要有一个天体稍微偏离一点点,这个运动形态就破溃了,譬如让中间的天体往另一个天体偏一点儿,我们知道引力是越近越强,一旦中心天体往另一个偏,它就会越发往那个天体偏,系统不会自发地回到初始状态,这叫作对于扰动的反馈不稳定。
但是两个小天体围绕一个大天体转这种情况是稳定解。我们在“极大篇”里已经讲过,天体的运动轨迹是做进动的椭圆,即便对于小的天体来说它的轨道有一些偏离,但它依然可以保持围绕大天体运动的整体趋势。这种运动模式不会破溃,所以是一个稳定解。
有了对稳定解的认知,我们可以尝试更换对混沌系统研究的目标,不再着眼于去找出它具体随时间变化的运动规律,而是去寻找它所有的稳定解。混沌系统的运动规律就是在稳定解之间切换,稳定解也并非百分百稳定,每一个稳定解都有一个稳定的限度,扰动在一个范围内可以回到原本的状态,但扰动若是过大就不行了。因此,稳定解的稳定性也是必须讨论的。
就像庞大无比的天气系统,显然就是个混沌系统。天气系统虽然变幻莫测,但它总是在几种特定的天气当中切换:晴天、阴天、雨天、雷暴、雪天、台风天等。这些天气情况,就是天气系统的局部稳定解,它们是天气系统的运动模式。
如此一来,我们研究混沌系统的目标就发生了变化:找出特殊解、稳定解,再去研究不同稳定解需要什么程度的扰动才会被破坏,被破坏以后会往什么方向发展,再去找到新的稳定解。
混沌系统与量子力学系统的区别
这里可以拿混沌系统和量子力学系统做一个类比。
量子力学系统也没有确定轨迹,但是可以通过波函数解出那些量子化、能量确定的稳定态。一个广义的量子态是若干个稳定态的叠加,这是哥本哈根诠释。测量的过程是一个叠加态的波函数坍缩到其中一个稳定态。与之类似,混沌系统也可以在不同稳定态之间切换。不相信哥本哈根诠释的人也许会认为,量子力学系统从本质上来说,也是一种微观的混沌系统。
这里触及了一个颇具哲学感的问题:什么是真随机?我们知道混沌系统从测量的角度来说,也是随机的。即便你知道整个混沌系统的规律是决定性的,但只要观察者所有的感知方式都无法预测这个系统,这个系统是否就可以被称为是真随机呢?如果真的如此,那么混沌系统的确定性加上高复杂度和高敏感度所达到的随机,与量子力学的真随机,在本质上是一样的,因为作为观察者,我们其实不能触及本质,只能依据我们的测量进行判断。但是量子纠缠的存在告诉我们,量子力学的随机如哥本哈根诠释所说,不光在测量上是随机的,在原理上也是个真随机系统。这是十分值得思考的。
第四节 耗散结构 (dissipativestructure)
混沌系统(或者说复杂系统)的存在非常重要,它是世界多样性的来源。根据熵增定律,宇宙作为一个系统,应当越发混乱。这就是热寂说(heat death of the universe)的核心内容,热寂说认为宇宙最终会达到熵最大的状态,没有任何秩序。
热寂说
根据热力学第二定律,也就是熵增定律,热寂说认为宇宙最终一定会发展成一团混乱,变得毫无规律。所有的物质都会混为一团,不会有星系、天体,更不会有地球这样富含生命的星球,因为各种天体,比如恒星、行星、地球的形成,生命诞生的本质都是秩序性的体现。然而熵增定律说的是,一个封闭系统最终一定会丧失秩序。这是因为秩序的熵是低的,要熵达到最高,必须尽可能消除秩序。
热寂说认为,宇宙最终会丧失一切秩序,变成“一锅汤”。但是我们的世界的存在,是一种反热寂说的现象。生命就是一种最高的秩序。
耗散结构
熵增定律有一个前提,就是对于一个封闭系统来说,熵永远不会自发减小。什么是封闭系统?封闭系统就是一个与外界没有能量交换的系统。
熵增定律在封闭系统中才成立。我们在“极大篇”中已经说到过,就目前人类对于宇宙的认知来说,宇宙是在不断膨胀的,为了加速膨胀还需要存在暗能量,也就是说宇宙还在不断被输入能量。这样看来,宇宙未必是个封闭系统。
为什么非封闭系统有可能逃脱热寂呢?这里就出现了非平衡态热力学中的一个概念——耗散结构。耗散结构是比利时的一位叫普里戈金(Ilya Prigogine)的理论物理学家兼化学家提出的概念。总的来说,就是在没有达到稳态的情况下,向一个不与外界隔绝的系统输入能量,它的熵有可能自发减小并呈现新的秩序。
新秩序形成的条件
你可以做这样一个实验:拿一个平底锅,锅里放薄薄的一层水,然后开始烧水,最好火要猛,上面再开个抽油烟机吸热。你会发现沸腾时的水面,可能会出现一种新的形状。一般情况下,沸腾的水面虽然会有很多水泡,但是这些泡泡是毫无规律的。但在水很薄,水的上下温差很大的情况下,水沸腾时的水泡会组成六边形的蜂窝状结构。
也就是说,当给水面输入足够能量,并且水处在沸腾的非稳定态时,水面形成了新的秩序,这种秩序自然是熵更小。这就是耗散结构的一个体现。总结这个实验,必须是水的上下温差达到一定的差值才会出现新的秩序,也就是输入能量的效率要足够高,并且系统要处在非平衡态。
为什么会出现这种逆熵的情况?为什么按理来说应当混乱的系统会出现这样的新秩序呢?关键在于混沌系统、复杂系统的非线性行为。复杂系统的性质多变,难以预测,因此也给新的秩序出现提供了可能性。
正是因为这种复杂性,地球上才能诞生生命。要知道生命系统异常复杂,生命延续的本质,都是要摄取能量,消耗能量以抵抗系统本身的熵增。恰恰是因为世界上存在非线性,存在混沌系统,存在足够高的复杂度,才能呈现出如此多变、如此多样的秩序性。
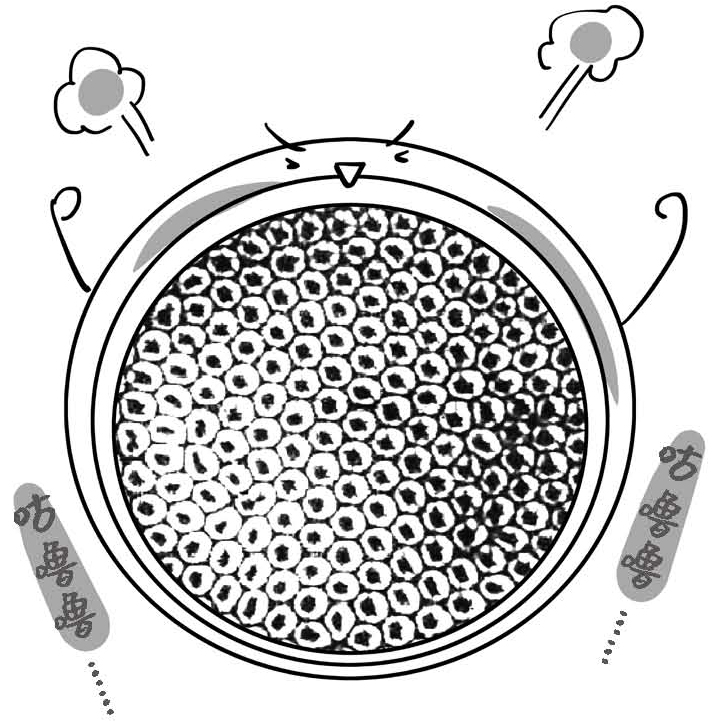
图17-3 沸腾的水面
至此,我们对于“极热篇”的知识讲完了。热力学、统计力学、复杂科学,可以说是经历了几百年依然非常蓬勃的学科。这些学科与其他学科的交叉性非常强,生物学、化学、生理学和医学走到理论化的程度,都与热力学、统计力学、复杂科学有着强烈的交叠。比如近年蓬勃发展的生物物理学,就是用物理(主要是统计力学)理论去解释生物中的一些基本现象,例如基因选择,DNA 的形成、转录,这里面物理学的道理其实很深刻。
研究现实世界,复杂科学和统计力学是最重要的理论武器之一,因为现实世界是复杂的,是大规模的。也正是因为在理论的底层有统计力学和复杂科学作为支撑,我们的世界才会形成今天的丰富多彩和千变万化。
