2.4.3 多源信息融合技术
多源信息融合可以定义为这样一个过程:把来自雷达和ADS-B等不同传感器和信息源的数据、信息加以联合、相关、组织,以获得探测目标的精确的状态和属性估计,以及对整体空情态势进行适时的综合评估。实施低空空域小目标探测有两种主要方法:一种是国际民航组织的未来空中航行系统(Future Air Navigation System,FANS)委员会推荐的广播式自动相关监视(ADS-B);另一种是雷达监视。这两种方法将在相当长的时间内共存。如何将ADS-B和雷达系统有效地融合在一起,最大限度地发挥它们的综合效力、提高监视精度,是每个监视管理系统低空慢速小目标检测亟须解决的问题。
通过采用合作式监视设备ADS-B与雷达互补探测方式,对合作式和非合作式目标实现全覆盖探测,提高低空空域飞行器的检测概率和检测精度。对合作式监视设备与雷达同时探测到的同一目标,由于合作式监视设备精度较高,因此通过合作式监视设备标校雷达数据的方法可提高低空目标探测精度,处理流程图如图2-54所示。
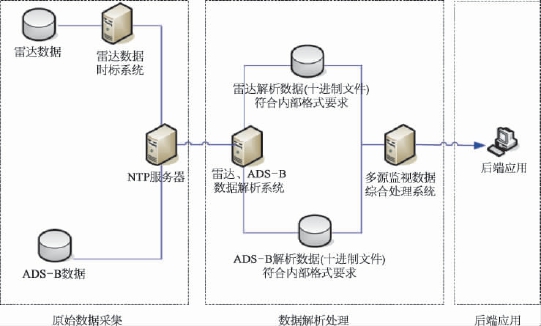
图2-54 ADS-B标校雷达数据处理流程图
由图2-54可知,ADS-B标校雷达数据处理流程总体上分为三个部分:原始数据采集、数据解析处理和后端应用。
1)原始数据采集
原始数据采集包括雷达原始数据采集和ADS-B原始数据采集。
雷达数据由雷达数据处理系统打上时标标签,在符合Cat001、Cat002和Cat008格式的雷达监视数据前添加6位时间字段,重新封装成带有时间字段的全新雷达报文。ADS-B数据采集通过集成与ADS-B接收机中的时标程序,将ADS-B数据打上时标标签,使ADS-B数据的时标标签和雷达数据时标标签都统一为网络时间协议(network time protocol,NTP)时间。
2)数据解析处理
原始的雷达数据和ADS-B 数据是二进制格式的,根据接口控制文件(interface control document)对雷达数据和ADS-B数据进行解析处理,并滤除原始数据中的校验信息和乱码信号。同时,由于雷达和ADS-B的更新率和位置坐标的差异,为了对比雷达和ADS-B的性能,需要将ADS-B数据和雷达数据进行时间、空间上的同步。
3)后端应用
数据处理中心同时接收到ADS-B数据和雷达数据后,需要在后端实现ADS-B数据与雷达数据的融合处理。通过坐标系校准和时戳比对,将多雷达数据和多ADS-B数据分别进行融合,生成一条多雷达航迹和一条多ADS-B航迹,再将多雷达航迹数据与多ADS-B航迹数据进行融合,生成系统航迹。这样能保证雷达监视与ADS-B监视的独立性,从而提高系统检测的精度。
然而,如果将ADS-B设备作为唯一的监视手段,一旦导航系统出现问题,将导致目标信息丢失。此外,对于未装载机载ADS-B发射机、发送虚假目标位置信息的非合作目标,仍需要采用一次雷达探测手段进行监视管理。通用航空飞行器升限较低、反射截面积较小、速度较低,其雷达回波容易淹没在杂波和噪声中。从噪声、杂波和干扰背景中检测出需要的慢速目标信号,是系统设计的一个难点。
在低空探测环境下的航迹关联判决中,航迹实际上存在着较大的模糊性。在目标密集、机动目标较多、探测环境复杂且系统包含有较大的传感器校准及转换和延迟误差的情况下,要判断来自2个局部节点的航迹是否属于同一个目标很困难,容易导致错关联、漏关联。可见,研究适合低空空域探测的多源数据管理和数据融合算法,是一项需要迫切解决的关键技术。
2.4.3.1 数据融合定义
数据融合是用于包含多个或多类传感器或信息源的系统的一种信息处理方法。Walz将多源信息融合定义为:通过对多个传感器产生的数据或信息进行监测、组合设计和关联等多级操作,得到关于观测环境或目标的精确状态、身份估计以及完整、及时的态势评估的过程。
在现有的空管系统以及低空探测系统中,常常通过一次雷达、二次雷达和ADS-B设备组网进行数据融合,将来源于不同体制、不同功能和不同频率的雷达系统的监视数据通过预处理、人工智能、过程优化等多技术综合运用,实现信息共享、整体探测、协同作战及体系对抗。从而提高探测性能、情报质量、抗干扰性能,实现高可靠性的低空空域监视,向用户提供通用、连续、及时、完整、准确的一体化空情信息,满足对空域低空微弱慢速小目标的探测要求。
2.4.3.2 数据融合的级别
按照数据融合系统中数据抽象的层级,融合可划分为三个级别:数据级融合、特征级融合和决策级融合。各个级别融合处理的结构分别如图2-55、图2-56和图2-57所示。
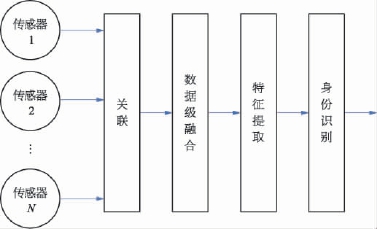
图2-55 数据级融合结构
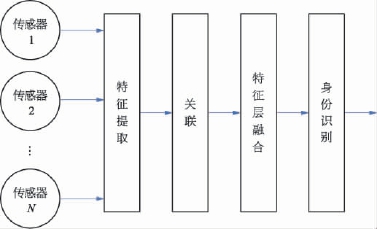
图2-56 特征级融合结构
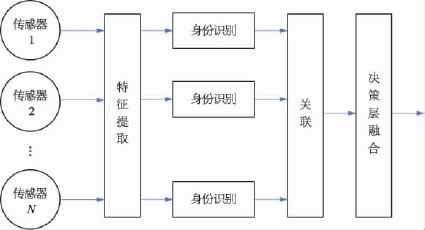
图2-57 决策级融合结构
1)数据级融合
数据级融合是最低层次的融合,其直接对传感器的观测数据进行融合处理,然后基于融合后的结果进行特征提取和判断决策。这种融合处理方法的主要优点是:只有较少数据量损失,并能提供其他融合层次所不能提供的其他细微信息,因此精度最高。它的局限性包括:
(1)所要处理的传感器数据量大,故处理代价高,处理时间长,实时性差。
(2)这种融合在信息的最底层进行,传感器信息的不确定性、不完全性和不稳定性要求在融合时有较高的纠错处理能力。
(3)它要求传感器是同类的,即提供对同一观测对象的同类观测数据。
(4)数据通信量大,抗干扰能力差。此级别的数据融合用于多源图像复合、图像分析和理解以及同类雷达波形的直接合成等。
2)特征级融合
特征级融合属于中间层次的融合,是由每个传感器先抽象出自己的特征向量(可以是目标的边缘、方向和速度等信息),然后融合中心完成特征向量的融合处理。一般而言,提取的特征信息应是数据信息的充分表示量或充分统计量。其优点在于实现了可观的数据压缩,降低对通信带宽的要求,有利于实时处理,但由于损失了一部分有用信息,因此融合性能有所降低。
特征级融合可划分为目标状态信息融合和目标特征信息融合两大类。目标状态信息融合主要用于多传感器目标跟踪领域,融合处理首先对多传感器数据进行数据处理,以完成数据校准,然后进行数据相关和状态估计;其具体数据方法包括卡尔曼滤波理论、联合概率数据关联、多假设法、交互式多模型法和序贯处理理论。目标特征信息融合实际属于模式识别问题,常见的数学方法有参量模板法、特征压缩和聚类方法、人工神经网络和K阶最近邻域法等。
3)决策级融合
决策级融合是一种高层次的融合,先由每个传感器基于自己的数据做出决策,然后在融合中心完成局部决策的融合处理。决策级融合是三级融合的最终结果,是直接针对具体决策目标的,融合结果直接影响决策水平。这种处理方法数据损失量最大,因而相对来说精度最低,但其具有通信量小、抗干扰能力强、对传感器依赖小、不要求是同质传感器和融合中心处理代价低等优点。常见算法有贝叶斯(Bayes)推断、专家系统、D-S证据推理和模糊集理论等。
特征级和决策级的融合不要求多传感器是同类的。此外,由于不同融合级别的融合算法各有利弊,因此为了提高信息融合技术的速度和精度,需要开发高效的局部传感器处理策略以及优化融合中心的融合规则。
2.4.3.3 数据融合模型
数据融合模型首先是由数据融合组织(Joint Directors of Laboratories,JDL)提出的,其后几经修改,形成面向数据融合结果的模型,如图2-58所示,该模型正被越来越多的实际工程系统所采用。
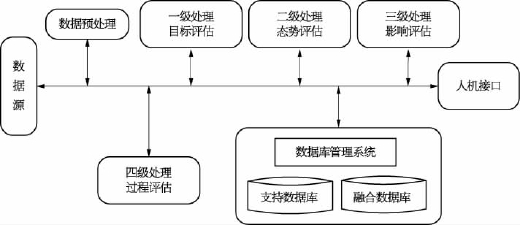
图2-58 JDL数据融合模型
该数据融合模型主要包括以下几种处理过程:
(1)第一级处理是目标评估(object assessment),如图2-59所示,主要功能包括数据配准、数据关联、目标位置和运动学参数估计,以及属性参数估计、身份估计等,其结果为更高级别的融合过程提供辅助决策信息。
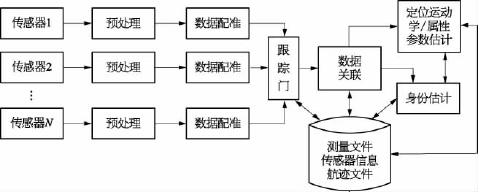
图2-59 一级处理中的目标评估模型
(2)第二级处理是态势评估(situation assessment),是对整个态势的抽象和评定。其中,态势抽象就是根据不完整的数据集构造一个综合的态势表示,从而产生实体之间一个相互联系的解释;态势评定则关系到对产生观测数据和时间态势的表示和理解。态势评定的输入包括时间检测、态势估计以及为态势评定所生成的一组假设等;态势评定的输出在理论上是所考虑的各种假设的条件概率。在军事领域,态势评估是指评价实体之间的相互关系,包括敌我双方兵力结构和使用特点,是对战场上战斗力量分配情况的评价过程。
(3)第三级处理是影响评估(impact assessment),它将当前态势映射到未来,对参与者设想或预测行为的影响进行评估。在军事领域指威胁估计(threat assessment),是一种多层视图处理过程,指有效遏制敌方进攻的风险程度。威胁估计包括通过汇集技术和军事数据库数据比对,对“我军”受敌人攻击的脆弱性、作战事件出现程度和可能性进行估计,并对“敌方”作战企图给出指示和告警。
(4)第四级处理是过程评估(process assessment),它是更高级的处理阶段。通过建立一定的优化指标,对整个融合过程进行实时监控与评价,从而实现多传感器自适应信息获取和处理、资源最优分配,最终提高整个实时系统的性能。对过程评估研究的关键主要集中在如何对系统特定任务目标以及限制条件进行建模和优化,以平衡有限的系统资源。
2.4.3.4 数据融合结构
数据融合结构可以分成以下三类:
1)集中式数据融合结构
这种结构要求把各传感器节点的原始信息都传递到融合中心,然后集中进行融合处理(图2-60)。它具有融合精度高、系统时延小的优点,同时还具有能明显增强系统探测概率的突出优点。然而,由于数据量很大,因此这种结构对中心处理机的处理能力和通信带宽的要求较高。
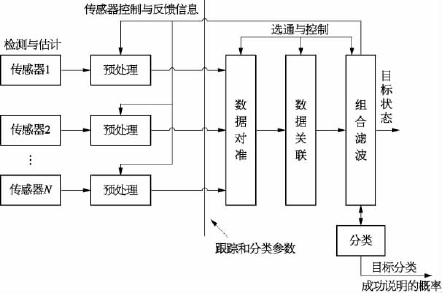
图2-60 集中式数据融合结构
2)分布式数据融合结构
在这种结构中每个传感器独立完成目标状态的估计,其估计结果作为融合中心的输入(图2-61)。此种结构可明显降低对融合中心处理机能力和通信带宽的要求,但系统融合精度不高、时延相对较大,特别是对低雷达截面积(radar cross section,RCS)目标的探测跟踪容易产生漏情。从数据融合结构的角度来看,中国目前的情报综合体系大多属于这种方式。
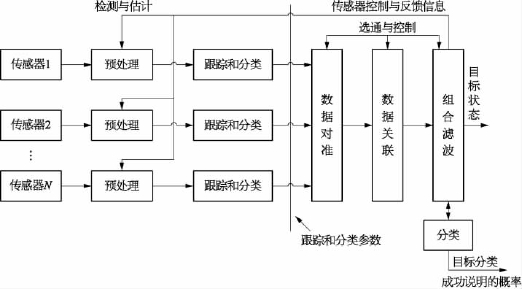
图2-61 分布式数据融合结构
3)混合式数据融合结构
混合式数据融合结构是前述两种方式的组合。这种结构在对处理机性能、通信带宽、系统时延、融合精度和探测概率的要求上得到了较好的折中,比较合理,目前已普遍应用于外军C4ISR系统中,近年来中国雷达组网也开始使用这种融合结构。混合式数据融合结构如图2-62所示。
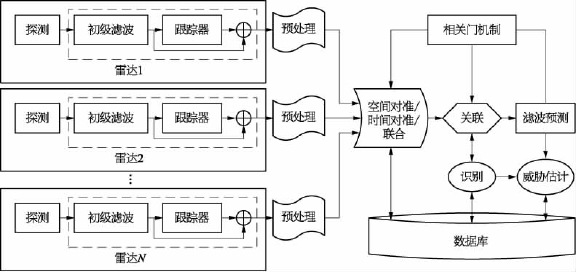
图2-62 混合式数据融合结构
混合式数据融合结构通过在雷达站进行一部分数据处理,然后发给中心处理机进行数据融合。这适当减轻了通信和处理的负担,因而推荐采用混合式数据融合结构。(https://www.daowen.com)
要完成对目标的跟踪、得到目标的航迹信息,数据融合中一个重要的步骤就是点迹融合。在低空监视系统中,点迹融合方式可分为两大类:点迹数据压缩合并方法和点迹数据串行处理方法。点迹数据压缩合并方法是指将多部雷达在同一时间对同一目标的点迹合并起来,将多个探测数据压缩成一个数据。合并之前,对于非同步采样的多雷达系统则可以采用时间校准和目标状态平移的方法,将异步数据变换成同步数据后再进行点迹压缩合并处理。点迹数据串行处理方法是指将多雷达数据组合成类似单雷达的探测点迹,用于点迹-航迹的互连(图2-63)。
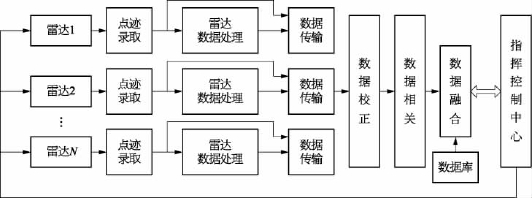
图2-63 数据融合系统原理框图
2.4.3.5 数据融合的关键问题
1)时间校准
多传感器信息关联及融合系统一般由多个异类传感器组成。异类多传感器与单传感器或同类传感器相比,其提供的信息更具有多样性和互补性,但由于每个传感器提供的观测数据都在各自的参考框架之内,导致产生的异类数据在时间上不同步,因此在对各传感器传输的信息进行处理之前,必须先将它们变换到同一个时间参考点框架中。
对于时间校准,一般通过外推和内插的方法进行,根据t′、t″时刻的观测位置与融合时刻ti的时间差,将多个传感器的异步测量数据转换为ti时刻的同步数据,便于进一步数据处理。其校准公式为
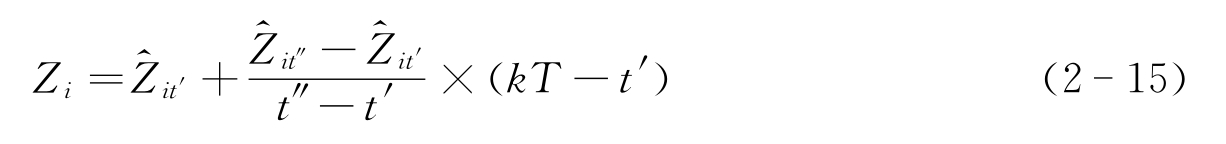
式中,k T 为融合的时间基准;Zi为k T 时刻的内插值;![]() 、
、![]() 分别为t′和t″时刻目标的鲁棒估计值。当t′=k T 或t″=k T 时,取
分别为t′和t″时刻目标的鲁棒估计值。当t′=k T 或t″=k T 时,取![]() 或
或![]() 作为多传感器信息融合的依据,进行信息关联及融合。
作为多传感器信息融合的依据,进行信息关联及融合。
2)空间配准及滤波坐标系的选择
在多雷达站点组网系统中,各雷达上报的目标点迹是相对各自站址参照坐标系而言的。各雷达空间坐标系不相同以及测量维数不匹配,使得信息关联及融合处理存在困难。因此,在进行多站信息关联及融合之前,首先将所有组网内雷达的测量值转换到统一的坐标系中,统一坐标系原点通常采取融合中心或主雷达位置,然后在统一的坐标系中进行相关、滤波和外推。在进行坐标变换时,如果系统覆盖区域很大,由于地球曲率的影响,坐标有畸变误差,会导致观测目标分裂。坐标变换对准一般是将以各传感器为中心的极坐标数据转换到地理经纬度坐标系,最后统一到以融合或数据处理中心为原点的坐标系实现。下面给出由雷达测量值求经纬度的计算公式(WGS-84模型)。
设地面上有一点H,在两种坐标系中的坐标为(x,y,z)H和(φ,j,h)H,则两坐标之间的变换关系为
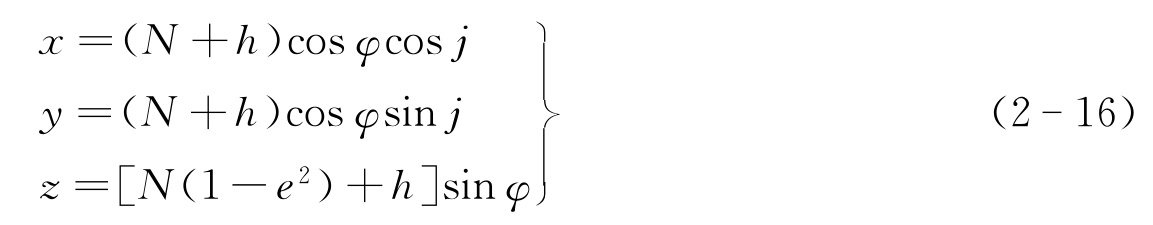
式中,![]() ,W=(1-e2sin2φ)1/2;
,W=(1-e2sin2φ)1/2;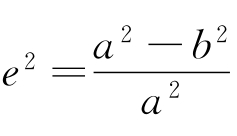 (a、b为地球椭球长短半轴)。
(a、b为地球椭球长短半轴)。
由(x,y,z)H化为大地地理坐标(φ,j,h)H:
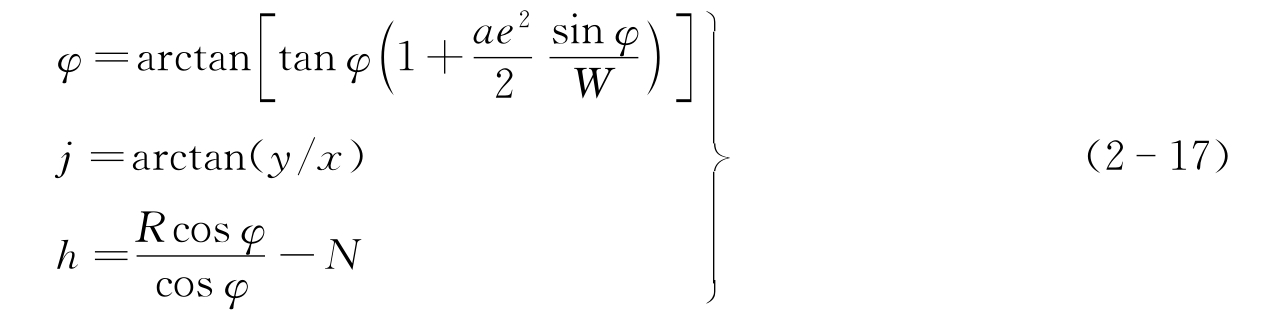
式中,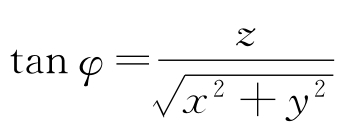 ;R=(x2+y2+z2)1/2。
;R=(x2+y2+z2)1/2。
3)数据关联及融合
由于多雷达系统的观测数据在空间域、时间域和粒度级别不同,因此需要判断来源于不同传感器的观测数据是否属于同一目标源。数据关联及融合可以定义为这样一个过程:把来自不同传感器和信息源的数据、信息加以联合、相关、组织,以获得探测目标的精确的状态和属性估计,以便对战场态势、威胁和重要程度的适时的综合评估。其主要包括两大部分:关联和融合。
数据关联是信息关联及融合的前提,它是决定从不同传感器中哪些测量/跟踪是代表同一个目标的处理过程。数据关联可在三个层次上进行:第一层是测量-测量关联,被用来处理在单个传感器或单个系统的跟踪初始上;第二层是测量-跟踪关联,被用于跟踪维持上;第三层是跟踪-跟踪关联,被用于多传感器的数据处理中。数据关联中采用最多的方法是序贯最近邻法,该方法是选择使统计距离最小或残差概率密度最大的回波作为目标回波,计算方法较简单;但其缺点是在实际中容易发生误跟和丢失目标。其他方法如联合概率数据关联方法,它全部考虑了跟踪门内的所有候选回波,并根据不同相关情况计算出各个概率加权系数以及所有候选回波的加权和即为等效回波,然后用等效回波更新多个目标的状态。此外,多假设跟踪法也是今后要考虑的方法之一。
信息关联及融合按融合级别划分为数据级、特征级和决策级。数据级融合是指在融合算法中,要求进行融合的传感器数据间具有精确到一个像素的匹配精度的任何抽象层次的融合;特征级融合是指从各部传感器提供的原始数据中进行特征提取,然后融合这些特征;决策级融合是指在融合之前,各传感器数据源都经过变换并获得独立的身份估计。信息根据一定准则和决策的可信度对各自传感器的属性决策结果进行融合,最终得到整体一致的决策。
2.4.3.6 数据关联及融合算法
数据关联及融合涉及多方面的理论和技术,如信号处理、估计理论、不确定性理论、最优化理论、模式识别、神经网络和人工智能等。很多学者从不同角度出发提出了多种信息关联及融合技术方案。图2-64对现有比较常用的信息关联及融合方法进行了归纳,主要分为经典方法和现代方法两大类。
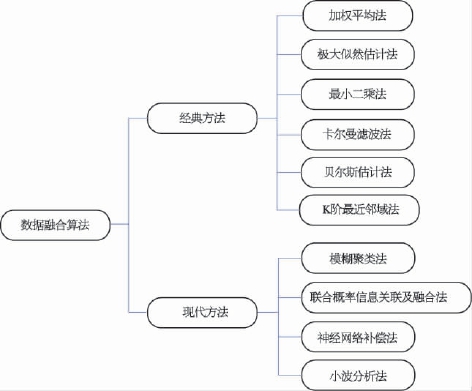
图2-64 常用的信息关联及融合算法
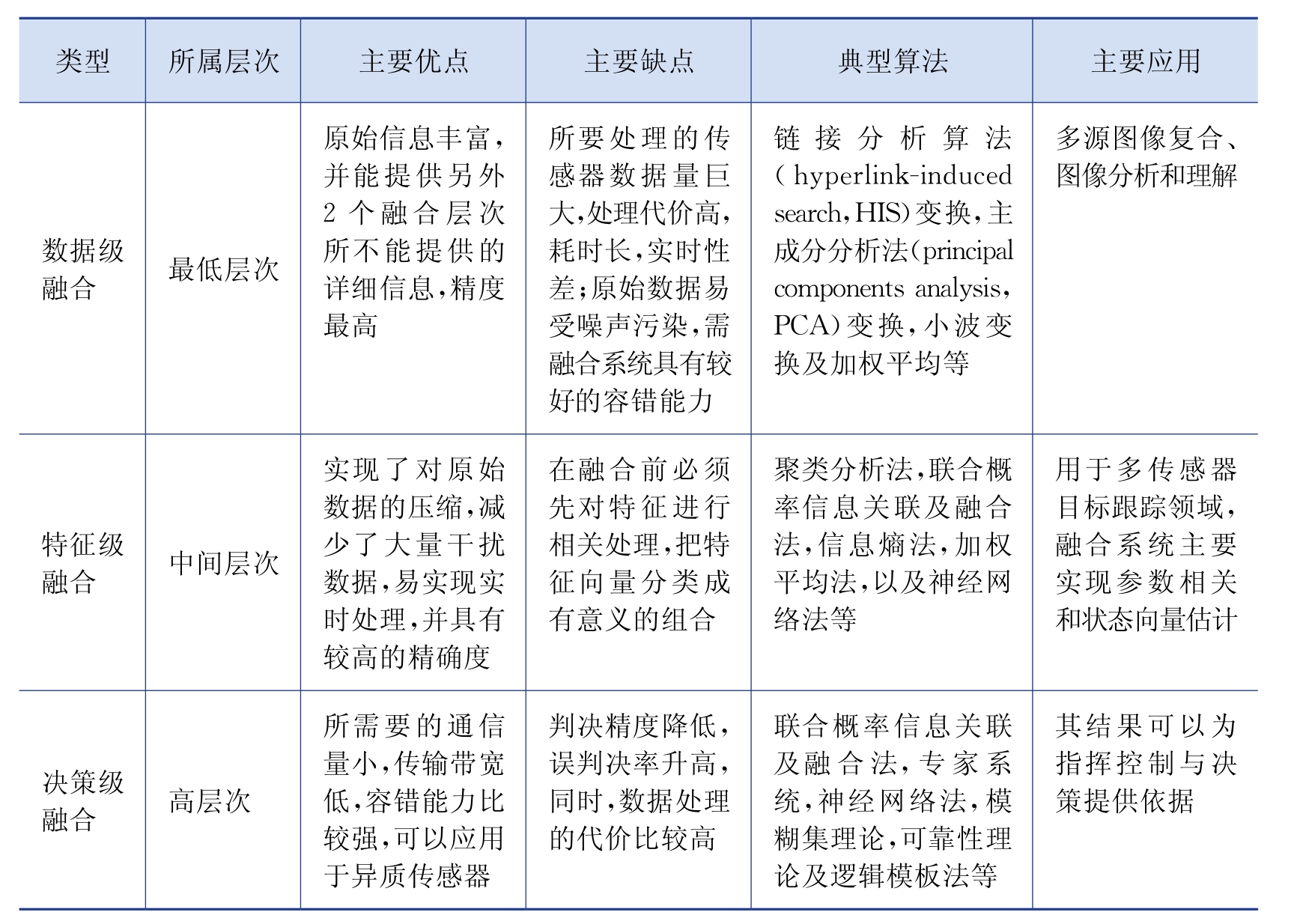
对信息关联及融合算法进行分类,也可按数据级融合、特征及融合和决策级融合不同信息层次进行(表2-3)。下面选择几种有代表性的算法做详细描述。
表2-3 不同信息层上信息关联及融合算法分类
1)加权平均法
加权平均融合法是工程实践中常用的方法之一。采用加权平均法进行航迹融合时,权值的分配对融合航迹精度的影响十分明显,分配得当,融合效果好;反之,融合后的航迹精度提高不大。下面对加权平均法进行详细描述。
(1)设定加权平均融合模型。设多雷达站点组网系统中有P部二维雷达,各雷达系统对同一目标进行跟踪处理,在ti时刻输出目标航迹的位置信息为[Rk(i),θk(i)](k=1,2,…,P;i=1,2,…,N)。其中,Rk(i)为第k 部雷达在ti时刻输出的目标距离信息;θk(i)为第k 部雷达在ti时刻输出的目标方位信息。
按加权平均法融合航迹的位置信息为[R(i),θ(i)],则
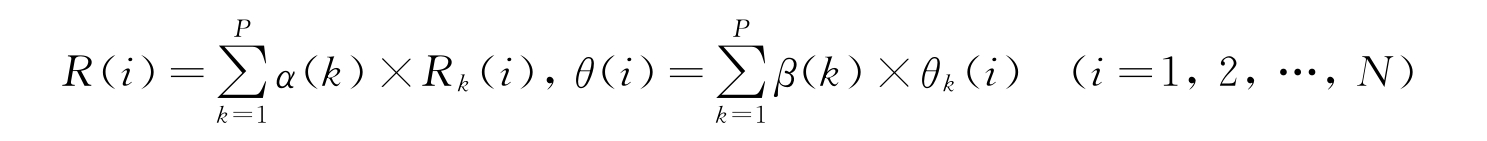
式中,α(k)(k=1,2,…,P)为距离加权平均融合时各雷达对应的权值;β(k)(k=1,2,…,P)为方位加权平均融合时各雷达对应的权值,且满足
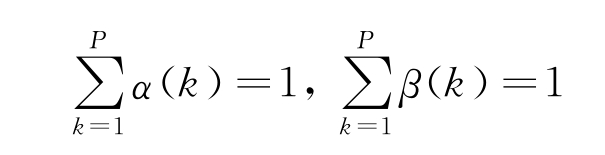
(2)最优权值分配原则。设多雷达站点组网系统中各雷达输出航迹的距离和方位精度分别为σR(k)、σθ(k)(k=1,2,…,P),则航迹加权平均融合的最优权值分配为
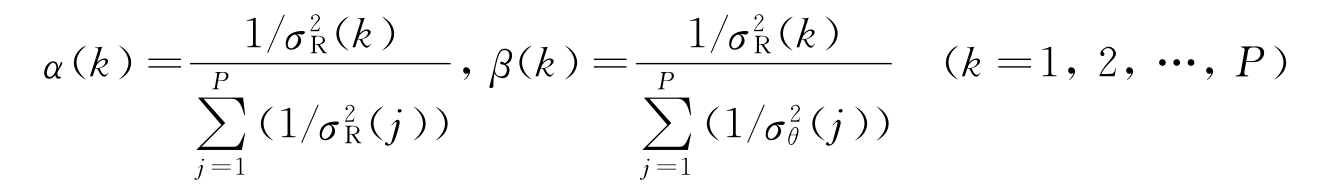
按上式进行权值分配融合航迹,其融合后的航迹距离和方位精度分别为
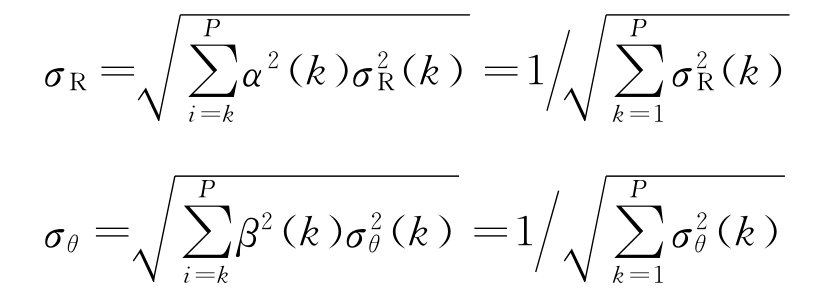
假设多部雷达的精度不相同,最低距离精度与最高距离精度分别为σr(min R)和σr(max R);最低方位精度和最高方位精度分别为σθ(minθ)和σθ(maxθ),可得
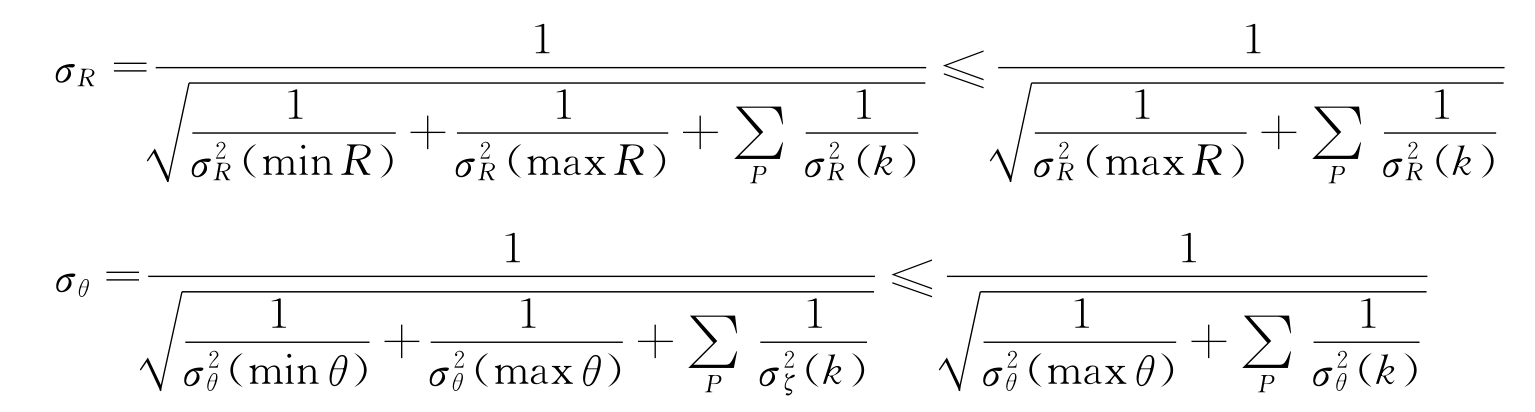
由上面式子可知,精度再差的雷达参与航迹融合,都有利于提高融合航迹的精度。最优权值分配与各雷达输出的航迹精度密切相关,即获得最优权值分配的前提是必须知道参与融合的各雷达输出航迹的准确精度。然而,在实际的工程应用中,通常只知道各雷达探测精度的标称值,无法得到各雷达输出航迹的精度或得到的精度不准确。因此,需要实时地对各雷达输出航迹精度进行修正,以确保各雷达输出航迹精度的准确性和获得动态的权值分配。
2)联合概率信息关联及融合法
联合概率数据关联(joint probabilistic data association,JPDA)算法是采用极大似然估计对多传感器多目标的同时/同周期的测量进行同源划分,然后对每个划分所得的源于同一目标的多测量进行融合处理,产生同一目标的联合测量值。这样就可以在该传感器测量系统中应用JPDA算法,实现对多目标的信息关联及融合。当存在某传感器测量精度较低甚至漏警的情况下,对源于同一目标的多测量融合能改善测量精度。
假设某测量时刻k,有N 个传感器对M 个空中目标进行测量,每个传感器有mn(n=1,2,…,N)个测量,记k 时刻总的测量集合为
式中,![]() ,n=1,2,…,N;N 为传感器n 的测量集合。总测量数目为
,n=1,2,…,N;N 为传感器n 的测量集合。总测量数目为
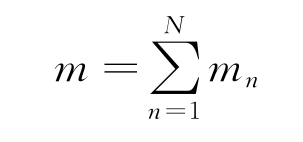
目标的状态方程和测量方程分别为
Xk=FkXk-1+Wk
Zk=HkXk+Vk
式中,Xk为目标在k 时刻的状态,包含有目标位置、速度、加速度等多维状态向量;Zk为多维测量向量;Fk为状态转移矩阵;Hk为测量矩阵;Wk、Vk为相互独立的高斯白噪声,其协方差分别为Qk、Rk。
在一个周期内,针对同一目标,来自N 个传感器的N 个测量序列为:{Z1(k),Z2(k),…,ZN(k)},定义这N 个测量的等权平均残差为dpn(k),则由卡尔曼滤波方程可得如下关系:
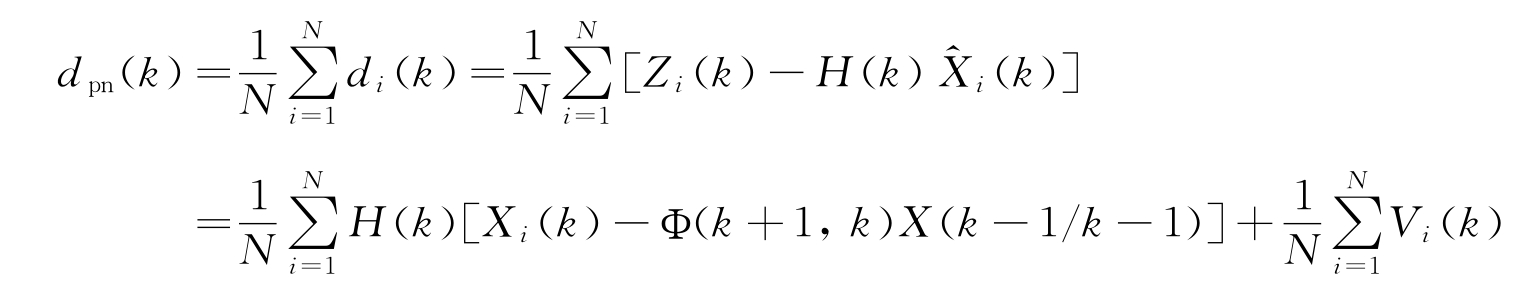
式中,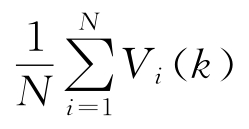 为等权平均测量噪声Vpn(k)。其协方差矩阵为
为等权平均测量噪声Vpn(k)。其协方差矩阵为
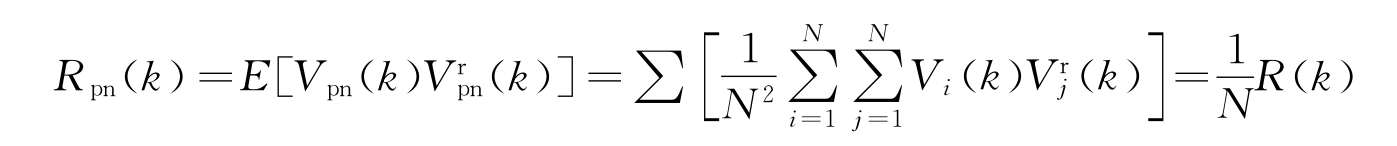
式中,R(k)为测量噪声V(k)的协方差矩阵。显然等权平均残差中随机测量噪声的影响已大大减少。当传感器为不同类型(尤其存在精度相对较低的传感器时),可以采用非等权平均,分析方法同上。
由以上分析可知,用这种包含更多目标信息而测量噪声影响更小的等权平均残差dpn(k)代替一次测量残差d(k)来计算目标状态估值,无疑会大大提高跟踪器的估计精度。
3)模糊聚类法
由于在航迹关联判决中,航迹实际上存在着较大的模糊性,而这种模糊性可以用隶属度函数来描述两个航迹的相似程度,因此就产生了模糊数学的方法。其中,模糊聚类法是一种新近的模糊数学方法,它利用观测数据的不确定性(即模糊性)把在某一时刻t得到的n 个测量数据分配给m 个航迹。从模糊聚类的观点来看,如果在某一时刻能把各传感器的测量数据进行正确的聚类,就可知在该时刻该观测空间出现的目标数,从而进行信息关联及融合。
下面对聚类算法关联及融合过程加以详细描述。
假设有两部不同雷达共同观测3个目标,如图2-65所示。

图2-65 两部雷达探测三个目标示意图
这里采用Rij表示探测目标的属性,其中,i=1,2;j=1,2。 现在的问题是判断R11、R12、R21、R22是否有属于同一目标的航迹。将这个问题作为对两个雷达的二值假设检验问题来考虑,用H1代表两条航迹是同一目标航迹,H0代表两条航迹是不同目标的航迹,即
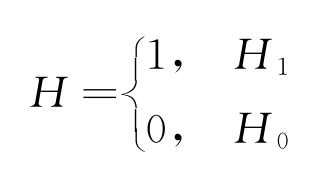
定义两条航迹的统计距离为
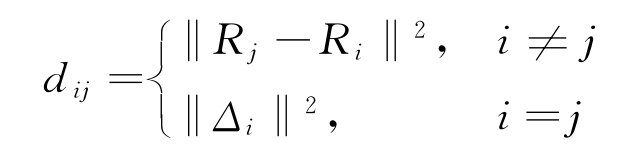
利用模糊聚类算法确定最佳dij{ }(i,j=1,2)元素之间的相似度矩阵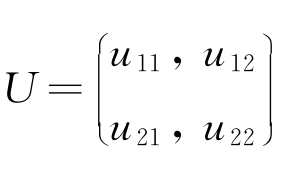 。
。
其中
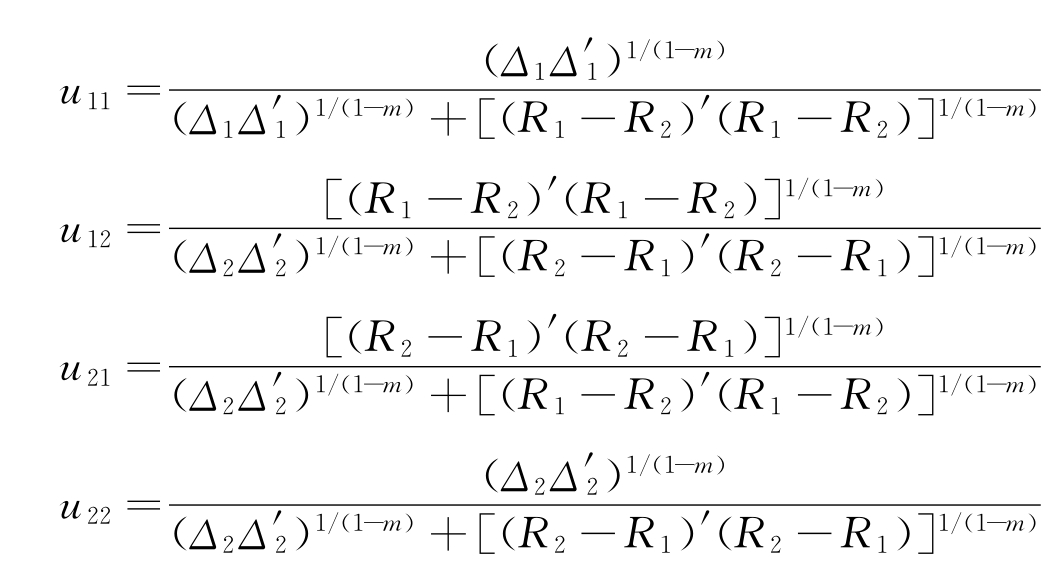
式中,m 为权重因子,通常取值范围为1~5。
关联决策Dij通常根据最小精度雷达决定。即
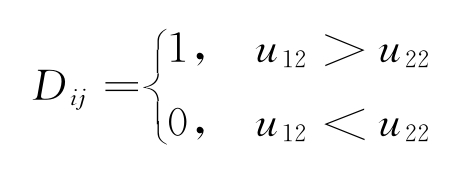
式中,Dij=1表示两条航迹隶属于同一探测目标;Dij=0表示两条航迹隶属于不同目标。
对于隶属于同一目标的两条航迹,可以进行航迹融合,得到精度更高的新航迹:
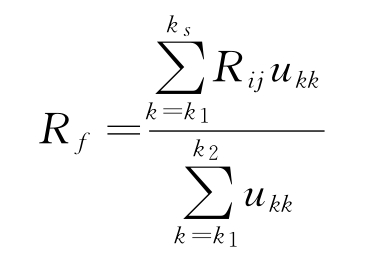
4)神经网络补偿法
神经网络补偿法的基本结构如图2-66所示,在融合中心首先对各个传感器的输出进行简单融合,然后引入径向基函数(radial basis function network,RBF)神经网络辅助简单融合来减少因交互式协方差或模型变化所引起的估计误差,这里神经网络的训练采用4个输入信号:2个为局部航迹的残余误差[εm(k),m=1,2],2个为传感器的当前状态估计值与当前状态预测值之差[Xm(k)-ΦXm(k-1),m=1,2]。
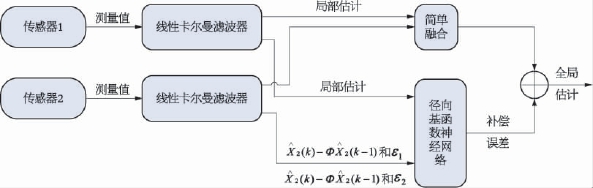
图2-66 基于神经网络补偿的航迹融合系统
对神经网络输入的选择主要基于以下考虑:交互式协方差主要是同卡尔曼滤波器的增益Km(k)相关,Km(k)可由滤波器的残差矩阵及Xm(k)和ΦXm(k-1)之间的差值获得,另外神经网络的输入Km(k)和Xm(k)-ΦXm(k-1)都是和过程噪声相关的。因此,神经网络的优化可使用误差(真实状态和基于简单融合的目标状态估计之间的差值)来训练神经网络:E=Xtrue-XSF。
神经网络的输出为误差E,将其作为观测值,并假定s(k)为n 维的状态向量,其均值为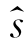 (k/k),方差为P(k/k),则其2n+1个序列点为
(k/k),方差为P(k/k),则其2n+1个序列点为
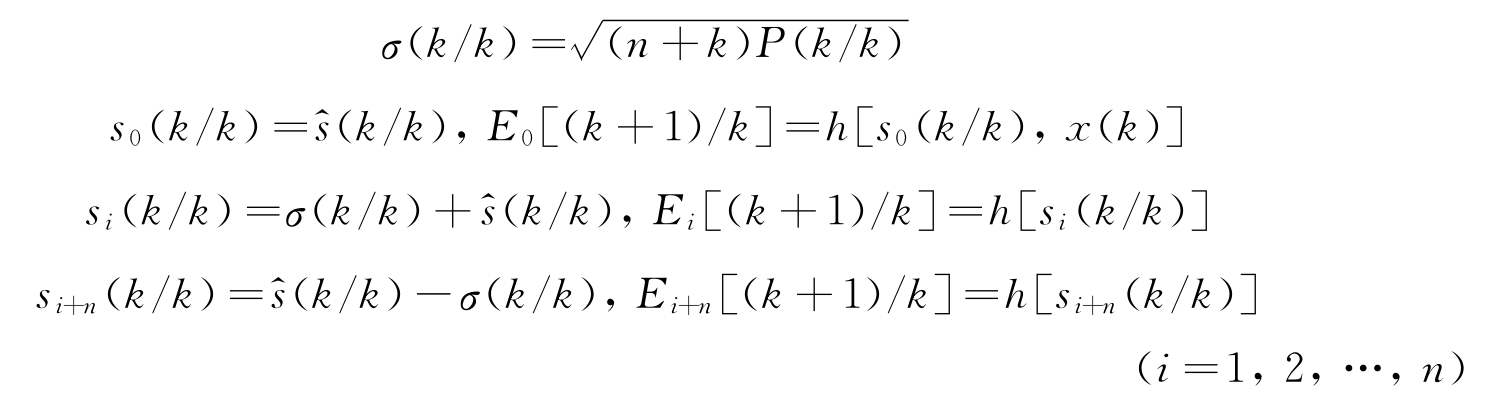
根据观测模型,计算测量值及方差为
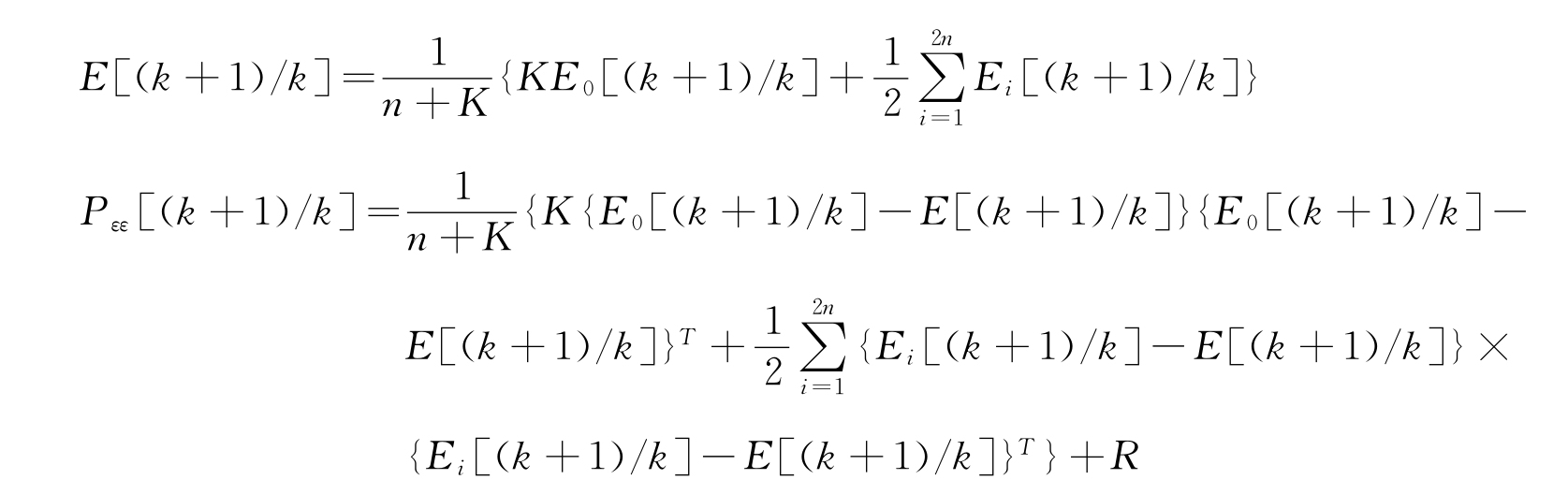
协方差为
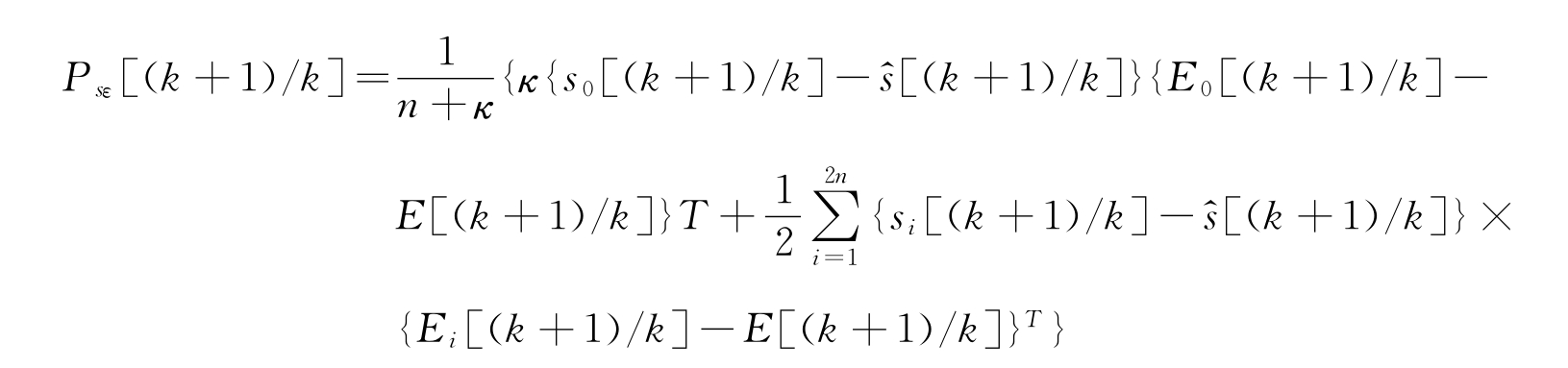
无痕卡尔曼滤波的增益及状态和方差的更新方程为
κ(k+1)=Psε[(k+1)/k]Psε-1[(k+1)/k]
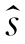 [(k+1)/(k+1)]=
[(k+1)/(k+1)]=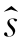 [(k+1)/k]+κ(k+1){E(k+1)-E[(k+1)/k]}
[(k+1)/k]+κ(k+1){E(k+1)-E[(k+1)/k]}
P[(k+1)/(k+1)]=P[(k+1)/k]-κ(k+1)Pεε[(k+1)/k]κT(k+1)
