4.3.1 卷积神经网络模型
卷积神经网络是一种深度的神经网络结构,具有监督学习的特点,其模型主要组成有:输入层、卷积层、池化层和输出层四种类型共同作用而成。其中隐含层的卷积层和池化层是实现卷积神经网络特征提取功能的核心模块。它在图像和视频确认、特色方言处理和推荐框架等领域具有广泛的应用。从网络架构的角度来看,卷积神经网络是一种神经网络系统,至少有一层中使用了不少于一个的卷积过程。卷积过程是在卷积层中执行。卷积层必须存在三个基本过程:卷积、池化和激活函数。卷积神经网络包含一堆卷积层和一个完整的执行层所追求的最大池化层。卷积层是整个网络模型中最重要的层,负责完成卷积任务。池化层位于卷积层之后,该层至关重要,因为如果出现较大的图片,则可训练的特征数量可能会异常大,这将延长了准备神经网络系统的时间,不满足实际需要,而池化层是用于减少图片的冗余信息。卷积核池化多次交替作用后将数据的抽象语义信息以全连接的方式输出。该网络模型采用梯度下降法最小化网络中权重参数的损失函数,逐层调节,通过反复训练迭代权值提高网络的精度。
由于目前卷积神经网络的应用领域主要在图像识别和文本处理,因此以经典的手写字符图像研究为例展开详细介绍。在手写字符图像的研究中,部署了由美国商务部发布的美国国家标准与技术研究院(National Institute of Standards and Technology,NIST)修改后的数据库,该数据库包含了大量手写字符图片。图4-14所示为神经网络中存在的各层的总体视图,第一层是输入层,第二层是卷积层,中间层是池化层和卷积层,网络的最后两层是完全连接的层和输出层。
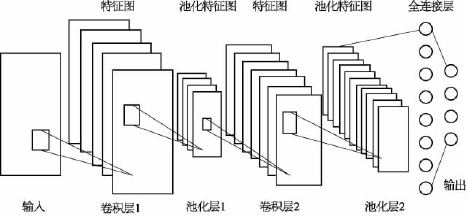
图4-14 卷积神经网络架构图
1)输入层
输入层是初始图像层,有助于系统体系结构前端的操作,输入层是字符图像,如图4-15所示。输入层可以是灰度图像或RGB图像。设输入层具有的尺寸为W ×H ×D,其中W×H 是图像的宽度和高度、D 是图像的深度。灰度的深度为1 px,RGB图像的深度为3 px。因此,如图4-15a所示,RGB图像的输入层具有32×32×3的尺寸;而如图4-15b所示,灰度图像的输入层具有32×32×1的尺寸。
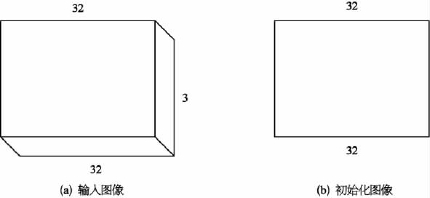
图4-15 输入图像的初始化
2)卷积层
卷积层为输入层之后的块结构,如图4-16所示,整个网络大部分计算工作都在卷积层完成。卷积层由具有学习能力的通道组成,并称为该层的组件。每个通道都被标识为一个过滤器,或称为卷积核。卷积核是一个空间宽度和长度(以像素为单位)的长方形矩阵,具有一定深度,这些通道覆盖了整个图像的信息量。假设卷积层中的模型通道的大小为5×5×3 px,其中宽度、长度和深度为5 px。这些通道被标识为阴影通道,并且使用的图像是RGB图像。卷积核的深度为1 px,大小为5×5×1 px,且所使用的字符图像为非彩色图像。
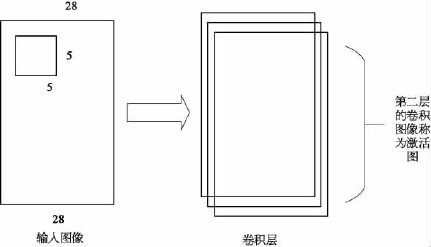
图4-16 卷积层视图
在神经网络操作的前向传递过程中,每个通道在宽度和长度上都与其他通道并排放置,以创建二维信息量。跨通道考虑字符形状的像素强度信息,并且通道中的其他区域显示为0 px。当每个通道穿过具有信息量的宽度和长度的通道横截面时,会从每个通道传递二维局部字符轮廓,从而在每个图像局部位置给出该通道的响应。
将卷积核部分卷积在整个图像上,并将卷积后生成的输出称为初始映射,初始化的图像被称为第二卷积层的激活图。卷积核的大小和数量取决于实验条件。目前没有明确的方法能够确定卷积核。在训练开始的时候,卷积核可以包含少量的随机值。但是其参数具有可学习能力,将随着网络的每个学习阶段而更新。假设输入层接收尺寸为W ×H×D的图像。卷积操作期间会部署其他两个超参数:卷积核的大小和步幅,以便确定下一层输入的尺寸W1×H1×D1。
W1和H1由下方公式给出,在这些等式中,P 称为填充,会在图像的每一侧引入新的零行和列:
W1=(F-W+P)/(S+1)
H1=(F-H+P)/(S+1)
3)池化层
池化层的位置在卷积体系结构中的卷积层之间。当图像过大时,池化层会减少特征的数量,并控制过度拟合。此外,在这一层中引入称为欠采样或下采样的本地池化方式,以消除每个图像的未使用元素并保留关键数据。池化层在每个深度的信息部分上自由工作,并在空间维度上更改信息。目前主要使用的四种池化方式为:最大池化、平均池化、全局最大池化和全局平均池化。最大池化是最常用的池化方式,是一种非线性下采样的方式,即取局部接受域中值最大的点,深度尺寸保持不变。在池化层中也可以采用不同的池化核,能够减小来自上层隐含层的计算复杂度,并且池化单元具有平移不变性,提取到的特征保持不变。
4)全连接层
全连接层通常作为卷积神经网络系统的末端。将来自池化层2的维度为W ×H 图像矩阵转换为一维矢量形式,并将其应用于网络系统。因此,引入这一层可以改善平衡趋势所追求的框架扩展。全连接层的数量取决于应用程序体系结构。在手写字符识别的研究中,假设有41个字符类,则此输出层有41个神经元,代表类别的数量。通过实验选择该层中的神经元数,得出全连接层具有256个神经元,完整的架构如图4-17所示。(https://www.daowen.com)

图4-17 手写字符识别研究的卷积神经网络架构
5)前馈传播方式
神经网络的部署通常遵循前馈传播方式。从输入层到输出层具有非循环连接的神经网络被定义为前馈神经网络。由于前馈神经网络与递归神经网络相比结构更简单,因此成为目前常用结构。在每一层中,神经元都具有来自上一层中某些(或全部)神经元的多个输入连接。这些连接称为突触权重,具有确定给定网络模型的功能。在前馈神经网络中,第k 层中神经元的状态定义为
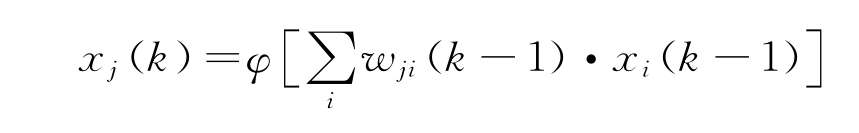
式中,xj(k)为第k层中第j个神经元的状态;wji(k-1)为第k-1层中第i个神经元与第k 层中第j 个神经元之间的突触权重;φ(·)为激活函数。从输入层到输出层的计算过程如上述公式,其称为前馈传播方式。
6)反向传播方式
卷积层通过推导网络中的反向传播更新向前传递,网络通过将卷积核对在其上一层的特征图上进行卷积操作构成特征图。在卷积层,将上一层的特征图与可学习的卷积核进行卷积,并通过激活函数来形成输出特征图。每个输出图可以将卷积与多个输入特征图结合。通常,其计算过程为
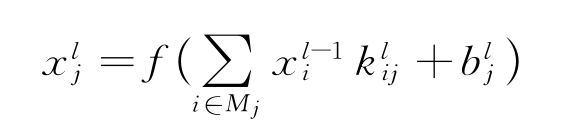
式中,Mj为输入特征图的选择;l为网络中的第l层;k为大小为S1×S2的矩阵;S1、S2为卷积核的长和宽;f(·)为非线性激活函数,通常是双曲正切或S型函数。每个输出特征图都有一个加性偏置。对于特定的输出特征图,输入图将与不同的卷积核k 卷积。换而言之,若输出特征图m 和图n 都在输入图i上求和,则应用于输出i的内核对于输出特征图m 和n 是不同的。
为了降低特征图xp~的误差,可以使用梯度Ep来相应地调整权重。通过对损失函数求导得到偏导数f′(·),其大小显示增加的方向,因此必须从权重wji中减去。这便产生了输出层中神经元的学习规则:
wij(t+1)=wij(t)+εyiδj
式中,δj=(T j-yj)f′(uj);其中,yj为输出层中神经元j的输出,yi为上一层中神经元i的输出。这表明激活函数必须是可微的,因此不能使用符号函数或阶跃函数,如S型函数:
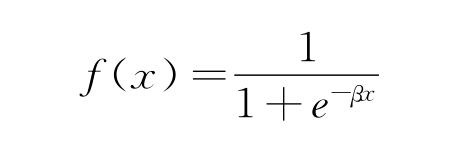
该函数不仅可以连续微分,还可以确保其值限制在0~1之间。隐藏层的学习规则为
wki(t+1)=wki(t)+εxkδi
式中,![]() )。输入层和隐藏层之间的权重由wij确定。因此,对隐藏层的每次权重调整都考虑了输出层的权重。隐含层中神经元i的权重调整是由输出层中的所有神经元的损失值共同确定,这取决于输出神经元的权重。由于产生的损失偏差被传递回隐藏层,因此称为反向传播方式。
)。输入层和隐藏层之间的权重由wij确定。因此,对隐藏层的每次权重调整都考虑了输出层的权重。隐含层中神经元i的权重调整是由输出层中的所有神经元的损失值共同确定,这取决于输出神经元的权重。由于产生的损失偏差被传递回隐藏层,因此称为反向传播方式。
7)卷积神经网络在信息融合中的优势
卷积神经网络作为多层感知器的一种特殊形式,能够处理二维数据,通过反向传播进行训练,具备卓越的容错性、并行处理方式和自学习能力,并且能实现传统神经网络机器学习的能力。因为卷积层的一个特征图中的所有神经元都具有相同的权重和偏差,所以参数的数量比完全互连的多层感知器中的要少得多,针对较大的图像数据量,能大幅减少训练过程的计算量,并且使etrain-etest的间隙隐性减低。池化层具有一个可训练的权重(局部平均系数)和一个可训练的偏置,因此,池化层中的自由参数数量甚至比卷积层中的自由参数更少。
因为具有较少的自由参数,所以卷积神经网络的训练比多层感知器的训练所需的计算量少得多。这对于隐性特征提取和一定程度对变形(位移、旋转和拉伸等)的相对不变性,使卷积网络成为分类任务(尤其是模式识别)明显的候选对象。目前,其已成功用于各种智能化模式识别任务,例如手写和面部识别等。
