4.3.2 基于卷积神经网络的航迹关联算法
结合航迹在时间维度上的历史相关信息与空间维度的相对状态信息,使用卷积神经网络分类的优势,从两两航迹状态估计的相似程度出发进行智能判决,提出了基于卷积神经网络的航迹关联算法。本算法采用多时刻历史相关局部航迹估计的综合考虑代替对航迹状态估计计算和更新过程。在密集目标环境下,航迹相关性更倾向于目标的运动状态的相似程度。因此,本算法将调整航迹数据中位置坐标估计,突出航迹运动状态表现。同时,为充分发挥卷积神经网络分类的优势,将航迹对关联问题转变为二分类问题,即是否关联。
4.3.2.1 关联度量准则
航迹关联算法的性能需要一个固定的关联度量准则来评判。以下列举三类概率作为航迹关联算法的评判准则:
(1)从不同节点处接收到属于同一目标的滤波航迹对并做出正确关联的概率Ec。
(2)应属于相同目标的滤波航迹对,分别与其他目标滤波航迹判断出关联的错误关联概率Ee。
(3)从不同节点处接收到应属于同一目标的滤波航迹,却被判断为不关联航迹的漏关联概率Es。
由上述三个概率可知,Ec+Ee+Es=1。由于在不同假设条件下三个关联概率难以给出准确的显性结果,因此采用统计方法,汇总对应三种关联情况的滤波航迹对数量,求出各关联概率。即如果令Nl为待关联的目标总数;Ne为错误关联的航迹的个数;Nc为正确关联的航迹个数;Ns为漏关联航迹的个数。则根据各关联概率定义可得
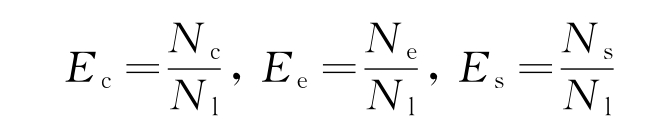
单次仿真所得结果具有不确定性,须做大量重复独立的蒙特卡洛实验,使得各关联概率的平均值接近某个固定值,得出统计结果。
4.3.2.2 航迹关联预处理主要步骤
在航迹融合过程中,为了融合的正确进行,来自多个传感器的初始数据必须要变换到相同的时空坐标系中。但在实际情况中,各个传感器之间存在偏差,并且在测量航迹数据的过程中会引入误差,因此在将不同的传感器数据转换到相同的时空坐标系下时,很难保证精度同时也很难发挥多传感器的优越性。因此,在多传感器信息融合的初始阶段,需要对此多传感器的初始数据进行预处理。初始数据的预处理技术是多传感器信息融合正确进行的前提条件。为了降低信息融合的数据处理计算量和提高目标的跟踪精度,必须寻找有效的测量数据的预处理方法。
在传统的航迹融合算法中,数据预处理一般为数据关联和数据融合两个步骤。为了适用于神经网络的使用和提高航迹关联性能,对数据进行整合和位置数据的调整。假设两个局部节点A、B。确定出多时刻历史相关估计的周期数为n,即当前关联时刻tk时,历史相关时刻为tk-n+1至tk。 融合中心接收的n 个周期数据为位置坐标估计[![]() ,
,![]() ],速度估计
],速度估计![]() 与航向角估计
与航向角估计![]() ,其中i=A,B。
,其中i=A,B。
将数据整合,参考卷积神经网络在图像数据方式中通常分别对图像RGB三个通道进行并行处理并整合,以此将两个节点的数据定义航迹关联中整合数据的两个通道,最后合并两个通道特征判断其相似度。则可得到整合数据{[![]() ,
,![]() ]、[
]、[![]() ,
,![]() ]、[
]、[![]() ,
,![]() ]、[
]、[![]() ,
,![]() ]},其数据大小为n×4×2。
]},其数据大小为n×4×2。
对位置坐标估计进行范围调整。由于分布式融合系统扩大了探测范围,因此可能会使得目标位置变化与目标位置的比例过小,在卷积神经网络训练过程中,可能会弱化此类数据的特征。因此,须调整整合数据中位置坐标估计,将其平移至贴合直角坐标系中横纵坐标轴,从而弱化位置因素影响,着重体现运动状态的关联性,但是相对位置仍然没有改变,对关联问题不存在影响。
处理过程中首先分别提取出航迹对中位置数据的横、纵坐标最小值:
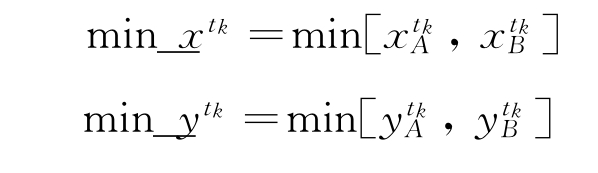
则调整数据为{[min_xtk,min_xtk],[min_ytk,min_ytk],[0,0],[0,0]},其大小为1×4×2。按第一个维度做重复扩充成三维调整数据,使其数据大小与整合数据大小n×4×2相匹配,得到Dad:
由上式调整整合数据获得Din作为坐标调整后的整合数据,同时也是基于卷积神经航迹关联算法中网络的输入数据。
4.3.2.3 网络模型构建(https://www.daowen.com)
将航迹关联问题转换为二分类问题。这需要对网络训练数据制定标签,而航迹关联的判决条件为对任意两条航迹的关联状态结果是否满足其标签信息。
首先定义航迹关联的依据:只有属于同一目标的并且融合时刻段对应的预处理航迹对才是关联航迹。然后为了定量给出离散状态有大小的意义,区分航迹对关联与否,在已知关联航迹数据库中给任意两条航迹打上相应的标签。定义关联航迹对的标签设置为1,不关联航迹对的标签设置为0。基于传统二分类器的方式,对标签做相应的独热编码。独热编码又称一位有效编码,其方法是使用N 位状态寄存器来对N 个状态进行编码,每个状态都有独立的寄存器位,并且在任意时候,其中只有一位有效。将对应1的独热编码为[1 0],对应0的独热码为[0 1]。则航迹对关联的标签变为[1 0],航迹对不关联的标签变为[0 1],也是网络输出的两种结果。由此可看出,采用独热编码的优势是定量处理了航迹关联问题中属性状态分类表示的问题,并且在一定程度上起到了扩充特征的作用。
根据上述标签制定方式能够确定在卷积神经网络模型中部分相对应的参数设置:输出层的激活函数和网络的损失函数的选择。本算法的网络模型功能实际上已经转变为实现二分类功能。而目前多类分类问题输出层的激活函数通常采用softmax函数,对应的目标函数通常采用cross-entropy,对应于本算法的网络模型功能。
1)激活函数softmax函数
假设有一个数组V,Vi表示V 中的第i个元素,那么这个元素的softmax值为
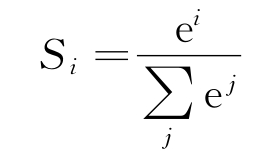
即该元素的指数与所有元素指数和的比值。其中能够将最大概率元素进一步放大。
2)损失函数cross-entropy函数
其表达式为
式中,目标类的tk为1;其余类的tk为0。与之前对标签独热编码结果相匹配。
根据已有的航迹对关联数据库,将分别来自两个不同局部节点的航迹两两结合组成航迹对,并为其打上对应标签。通过之前描述的预处理方法构建用于训练和测试的航迹关联数据集。经过网络训练后,获得用于航迹关联的卷积神经网络模型。该模型对固定类型的两个传感器观测航迹关联具有通用性。用于航迹关联的卷积神经网络模型获取流程如图4-18所示。
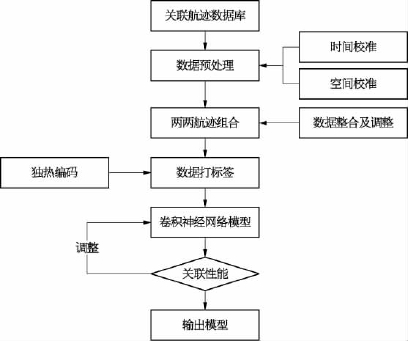
图4-18 网络模型获取流程
根据周期数为8,调整出用于航迹关联的卷积神经网络模型为4层卷积层、1层池化层、1层Batch Normalization层、1层Flatten层和2层全连接层,具体参数见表4-2。其中,Batch Normalization层是一个自适应的重新参数化的方法,一般用于克服神经网络层数加深导致模型难以训练,防止过拟合;Flatten层是把多维的输入一维化,常用在从卷积层到全连接层的过渡,目前在卷积神经网络上效果显著。优化方式选择rmsprop算法进行训练优化,池化层采用平均二维池化方式。
4.3.2.4 算法流程
基于卷积神经网络的航迹关联算法完整的流程如下(图4-19):
(1)融合中心从各局部节点i=1,2,…,n 接收测量航迹集合Un={u1,u2,…,un}。
(2)对测量航迹做预处理,包括时间校准、空间校准和数据整合及位置信息调整Dm={d1,d2,…,dm}。
(3)对来自两个不同局部节点的航迹两两组合,获得判断关联的航迹对集合![]() ={
={![]() ,
,![]() ,…,
,…,![]() }。
}。
表4-2 网络层参数
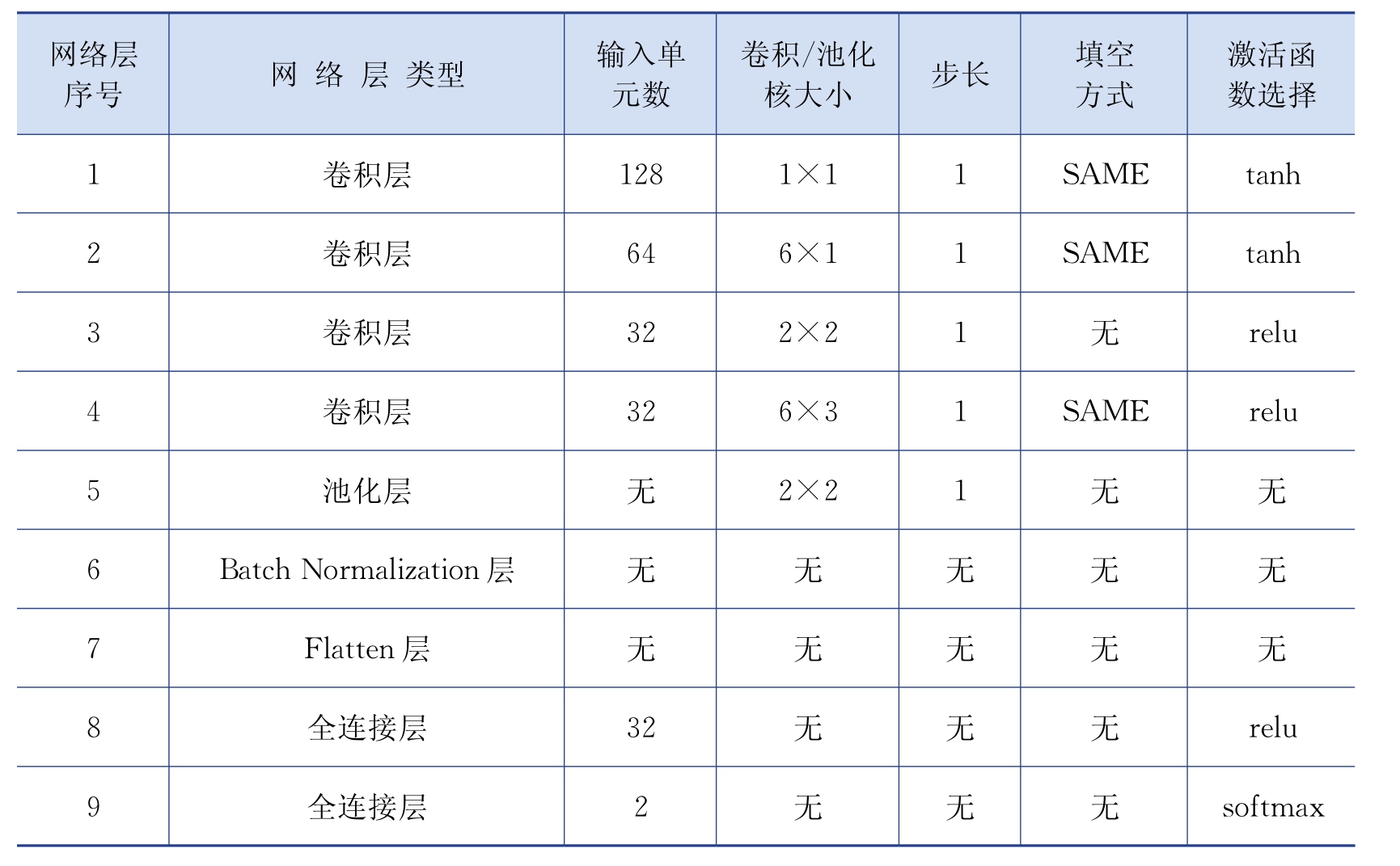
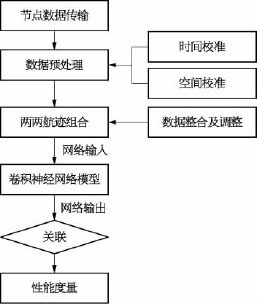
图4-19 基于卷积神经网络的航迹关联算法流程图
(4)使用经过训练完成的卷积神经网络模型对数据进行预测,输出预测的分类结果Pm={p1,p2,…,pm}。
(5)根据分类结果确定对应的状态属性判断航迹对是否关联。
(6)对算法的关联性能进行评估。
