1.3.1 计算机中常用的记数制
1.3.1 计算机中常用的记数制
1.进位记数制及相关概念
(1)进位记数制
用若干数位(由数码表示)的组合去表示一个数,各个数位之间是什么关系,即逢“几”进位,这就是进位计数制。日常生活中,通常是以十进制来进行计算的。另外,还有二进制、八进制和十六进制等。
(2)数码
数码:一个数制中表示基本数值大小的不同数字符号。
例如,十进制有10个数码:0、1、2、3、4、5、6、7、8、9。
(3)基数
基数:在进位记数制中每个数位上允许使用数码的个数称为基数。
例如,十进制的基数为10,八进制的基数为8,二进制的基数为2,+的基数为16。
(4)权和权的展开式
权:以基数为底、数码所在位置的序号为指数的整数次幂(整数部分个位的位置序号为0),称为这个数码的权。
权的展开式:对任何一种进位记数制表示的数都可以写出其按权展开的多项式之和。
任意一个r进制数可表示为:
N=an-1rn-1+an-2.rn-2+…+a1.r1+a0.r0+a-1.r-1+…+a-m.r-m
其中:ai为数字符号,ri为位权,n、m为整数。
例:将十进制数456.24写成按权展开式形式为:
456.24=4×102+5×101+6×100+2×10-1+4×10-2
2.计算机中常用的记数制
(1)二进制
二进制有如下特点:
① 有两个数码:0、1。
② 基数:2。
③ 逢二进一(加法运算),借一当二(减法运算)。
④ 按权展开式。对于任意一个n位整数和m位小数的二进制数D,均可按权展开为:
D=Bn-1.2n-1+Bn-2.2n-2+…+B1.21+B0.20+B-1.2-1+…+B-m.2-m
例:把(11001.101)2写成展开式,它表示的十进制数为:
1×24+1×23+0×22+0×21+1×20+1×2-1+0×2-2+1×2-3=(25.625)10
(2)十进制
十进制的特点如下:
① 有10个数码:0、1、2、3、4、5、6、7、8、9。(https://www.daowen.com)
② 基数:10。
③ 逢十进一(加法运算),借一当十(减法运算)。
④ 按权展开式。对于任意一个n位整数和m位小数的十进制数D,均可按权展开为:
D=Dn-1.10n-1+Dn-2.10n-2+…+D1.101+D0.100+D-1.10-1+…+D-m.10-m
例:将十进制数456.24写成按权展开式形式为:
456.24=4×102+5×101+6×100+2×10-1+4×10-2
(3)八进制
八进制的特点如下:
① 有8个数码:0、1、2、3、4、5、6、7。
② 基数:8。
③ 逢八进一(加法运算),借一当八(减法运算)。
④ 按权展开式。对于任意一个n位整数和m位小数的八进制数D,均可按权展开为:
D=On-1.8n-1+…+O1.81+O0.80+O-1.8-1+…+O-m.8-m
例:(5346)8相当于十进制数为:
5×83+3×82+4×81+6×80=(2790)10
(4)十六进制
十六进制有如下特点:
① 有16个数码:0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。
② 基数:16。
③ 逢十六进一(加法运算),借一当十六(减法运算)。
④ 按权展开式。对于任意一n位整数和m位小数的十六进制数D,均可按权展开为:
D=Hn-1.16n-1+…+H1.161+H0.160+H-1.16-1+…+H-m.16-m
在16个数码中,A、B、C、D、E和F这6个数码分别代表十进制的10、11、12、13、14和15,这是国际上通用的表示法。
例:十六进制数(4C4D)16代表的十进制数为:
4×163+C×162+4×161+D×160=(19533)10
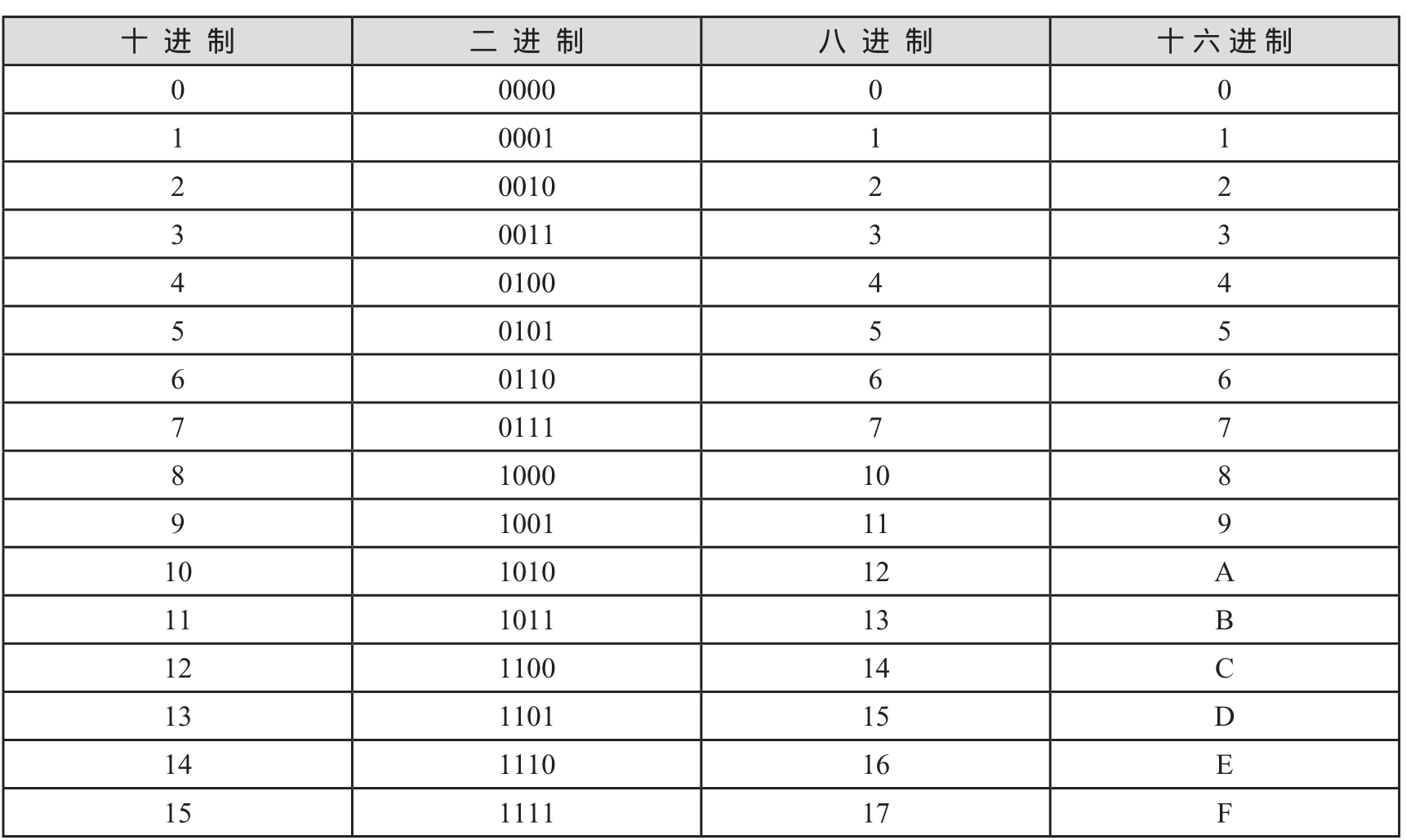
二进制数与其他数之间的对应关系如表1-3-1所示。
表1-3-1 几种常用进制之间的对照关系