1.3.2　不同进制数之间的转换

1.3.2　不同进制数之间的转换

不同进制数之间的转换是指十进制、二进制、八进制和十六进制数之间的转换。归结为三类。

1.R进制转换为十进制（二、八、十六进制数转换为十进制数）

转换规则是：按权展开，各项相加求和。

例：把（1101100.111）₂转换成十进制。

（1 101 100.111）₂=1×2⁶＋1×2⁵＋1×2³＋1×2²＋1×2^-1＋1×2^-2＋1×2^-3

　　　　　　　=64＋32＋8＋4＋0.5＋0.25＋0.125

　　　　　　　=（108.875）₁₀

例：把（19BC.8）₁₆转换成十进制数。

（19BC.8）₁₆=1×16³＋9×16²＋B×16¹＋C×16⁰＋8×16^-1

　　　　　　　=4 096＋2 304＋176＋12＋0.5

　　　　　　　=（6 588.5）₁₀

2.十进制转换为R进制（十进制数转换为二、八、十六进制数）

十进制转换成R进制，分别对数值的整数部分和小数部分进行转换后相加。

（1）整数部分的转换规则是：采用“除以基数取余”的方法，即反复除以基数，取其整数，直到商为0为止，然后逆向取余。

例：将（126）₁₀转换成二进制数。

结果为：（126）₁₀＝（1111110）₂

（2）小数部分的转换规则是：采用“乘以基数取整”的方法，即乘以基数，取整数部分，直到精确地转换或者根据精度要求转换到一定的位数为止。

例：将十进制数（0.534）₁₀转换成相应的二进制数。

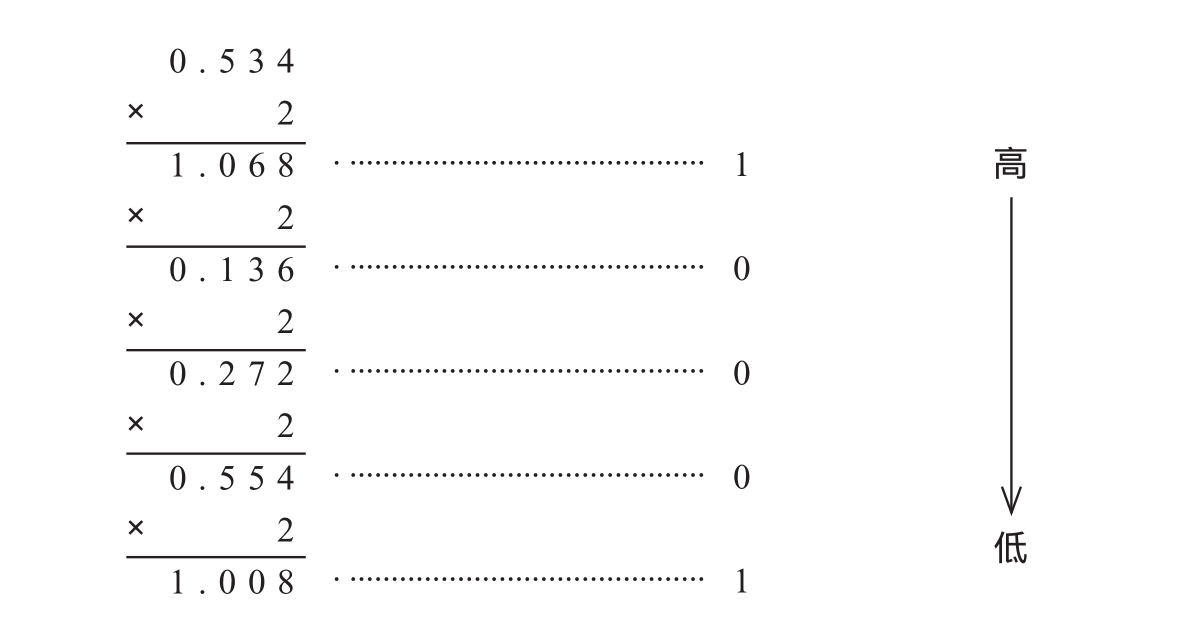
结果为：（0.534）₁₀＝（0.10001）₂

例：将（50.25）₁₀转换成二进制数。

分析：对于这种既有整数又有小数部分的十进制数，可将其整数和小数分别转换成二进制数，然后再把两者连接起来即可。

因为（50）₁₀=（110 010）₂，（0.25）₁₀=（0.01）₂

所以（50.25）₁₀＝（110 010.01）₂

3.八进制与二进制之间的相互转换

（1）八进制转换为二进制数

八进制数转换成二进制数所使用的转换原则是“一位拆三位”，即把一位八进制数对应于三位二进制数，然后按顺序连接即可。

例：将（64.54）₈转换为二进制数。

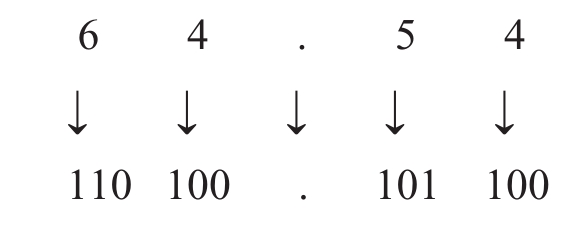
结果为：（64.54）₈＝（110 100.101100）₂

（2）二进制数转换成八进制数

二进制数转换成八进制数可概括为“三位并一位”，即从小数点开始向左右两边以每三位为一组，不足三位时补0，然后每组改成等值的一位八进制数即可。

例：将（110 111.11011）₂转换成八进制数。

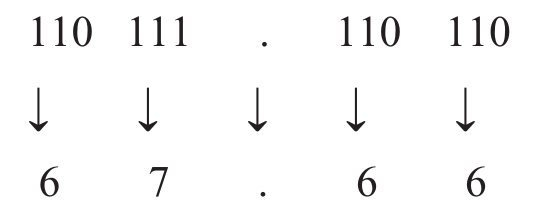
结果为：（110 111.11011）₂＝（67.66）₈

4.十六进制与二进制之间的相互转换

（1）二进制数转换成十六进制数

二进制数转换成十六进制数的转换原则是“四位并一位”，即以小数点为界，整数部分从右向左每4位为一组，若最后一组不足4位，则在最高位前面添0补足4位，然后从左边第一组起，将每组中的二进制数按权数相加得到对应的十六进制数，并依次写出即可；小数部分从左向右每4位为一组，最后一组不足4位时，尾部用0补足4位，然后按顺序写出每组二进制数对应的十六进制数。

例：将（1 111 101 100.0001101）₂转换成十六进制数。

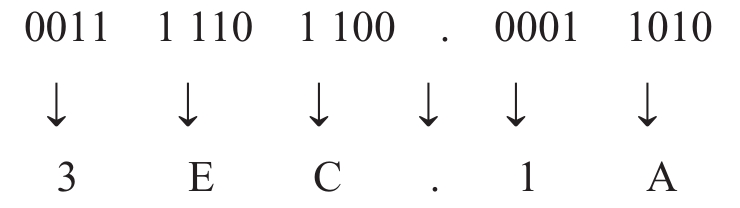
结果为：（1 111 101 100.0001101）₂＝（3EC.1A）₁₆

（2）十六进制数转换成二进制数

十六进制数转换成二进制数的转换原则是“一位拆四位”，即把1位十六进制数写成对应的4位二进制数，然后按顺序连接即可。

例：将（C41.BA7）₁₆转换为二进制数。

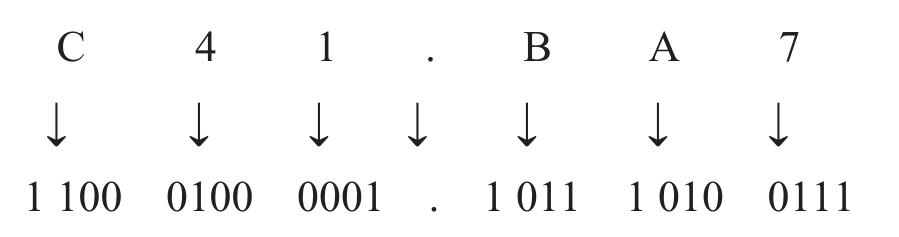
结果为：（C41.BA7）₁₆＝（110 001 000 001.101110100111）₂

在程序设计中，为了区分不同进制，常在数字后加一英文字母作为后缀以示区别。

十进制数，在数字后面加字母D或不加字母也可以，如6 659D或6 659。

二进制数，在数字后面加字母B，如1 101 101B。

八进制数，在数字后面加字母O，如1 275O。

十六进制数，在数字后面加字母H，如CFE7BH。