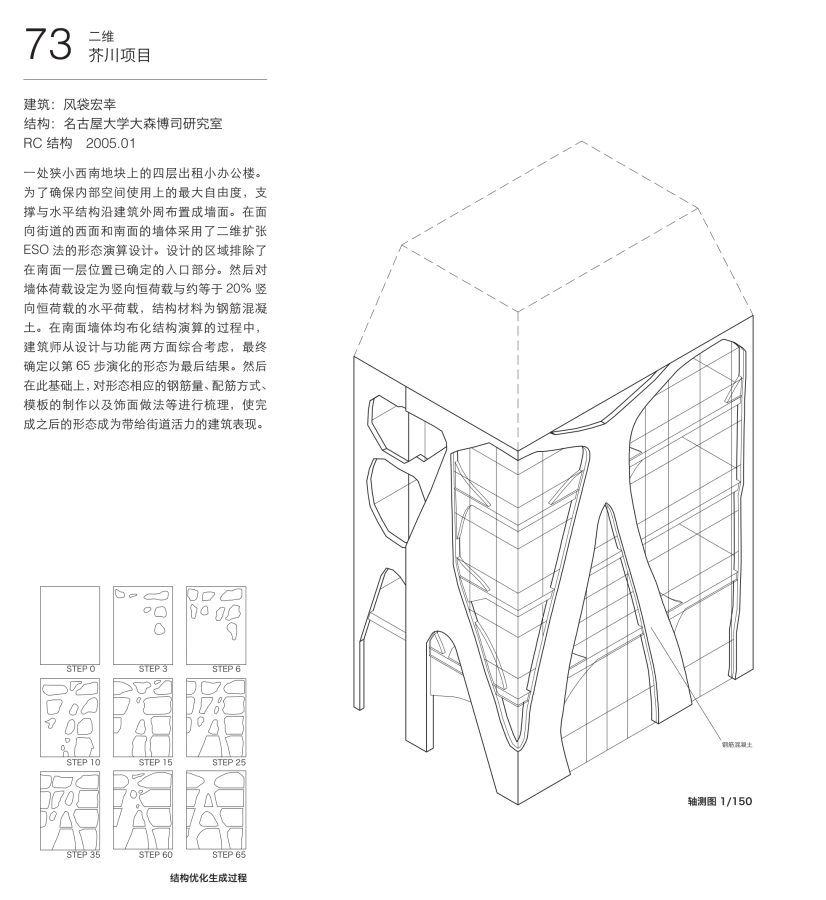
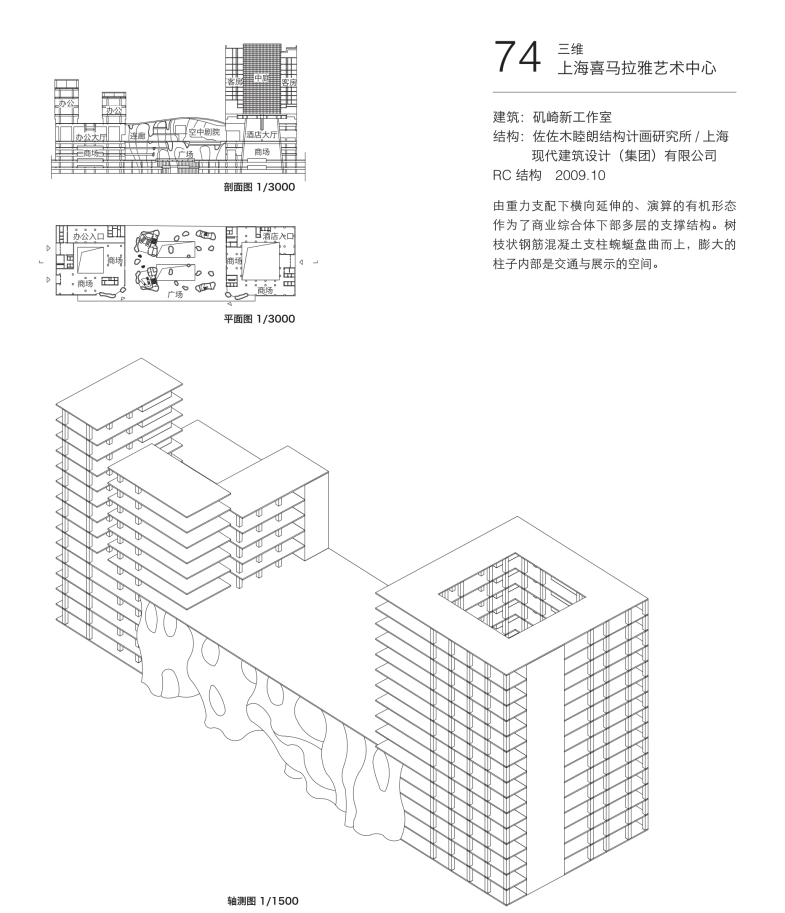
4.4 流动的结构
在1995年2月举行的“横滨港大桟桥国际客船站”国际竞赛中,F.O.A事务所的竞赛方案赢得了最终胜利,它向人们展现了一个不同于以往的建筑与城市两分的状态。候船大厅仿佛从街道上直接延伸而出,由一系列缓坡流动的曲面楼板形成 “地景”。这当中没有传统意义上的楼梯,也没有可以清晰辨认的楼板,没有内外之别,没有整齐排列的房间和走廊,甚至没有清晰的楼层。有机、曲面、连续是这个建筑设计方案带给人们的全部印象。与其说它是一个建筑,倒更不如说是一处从街道中生长出来的自然平台。F.O.A的竞赛方案颠覆了对建筑固有的定义,模糊了建筑、景观、城市之间原本清晰的边界。更为重要的是,它向我们展现了一个“计算机建筑设计时代”的到来,以及一个“无所不能的建筑时代”的到来。
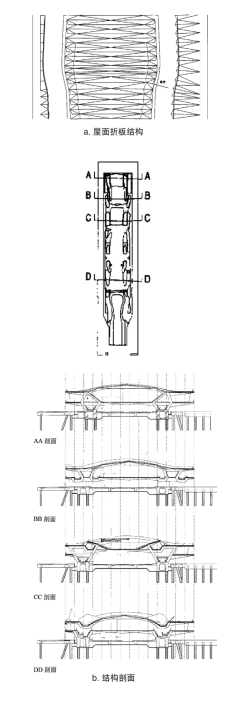
图4.12 横滨港大桟桥国际客船站
然而,就是这样一个未来一般的建筑,使得人们对于其如何实现,以及将要付出的代价产生了诸多疑问。正如这个项目的结构设计师渡边邦夫所言,“大项目(Big Project)诞生时需要的是运气”12。当时正值横滨市被确定为“2002年韩日世界杯”冠军赛的主办地,横滨市政府在一片质疑声中,毅然决定实施这个方案。然而,现实中的技术难度远远超过了人们的想象,正像F.O.A在建筑竣工后所言“这个项目如果没有结构设计集团是不可能实现的”13那样,初出茅庐的年轻建筑师在面对如何实现这座建筑的结构问题上,显得茫然而不知所措。竞赛方案时提交的结构设想是试图将楼板一边进行翻折,一边形成有机的曲面,以此来取代通常的梁板柱。并且楼板需要采用蜂窝板的形式,上下表面的钢板之间充填“夹心材”。对于竞赛方案的结构设想,结构设计集团将结构必要的厚度计算后提交给建筑师进行形态修正。如此由建筑方修正楼板上表面的步行空间边界,结构方确定楼板底面下层空间顶部的轮廓,中间的“夹心材”则由双方共同商量确定。然而结构验算表明,当初建筑师提出的结构方案仅涉及了形态上的考虑,而没有考虑楼板结构的面外受力和应力集中等问题。因此,原先建筑师所设想的楼板折面结构是不成立的。为此,结构设计集团提出在楼板底面采用折板结构来增加楼板刚度,历经两年反复的调整与修改,建筑与结构终于确定了建筑形态的轮廓 :楼板底面呈折板形,而上部本身由于结构要求也呈凹凸不平状,通过在楼板上部架设木板层的方式解决。其最终设计结果已然同竞赛方案大相径庭了。然而这样非同寻常的形态仍然使得结构难以找到可以确立的几何形态。为了全面地了解建筑形态的整体架构,结构设计集团以人体CT扫描的方式在沿建筑长边方向每隔15m切取剖面,将整个建筑切成10段,然后再分别对每部分单独进行结构模型解析。当渡边邦夫在最后施工图设计全部完成的时候,望着被堆放到一起的10段局部模型时,终于意味深长地反省道:“我现在终于感受到计算机的恐怖了……这里没有一处剖面是相同的,这难道不是混沌吗?到底应该如何施工啊!”的确,尽管异常艰难地完成了设计,但是计算机图形设计的随意所带来的困难远远没有结束。施工的难度超过了预想,即便是最优秀的工程师,也很难将一个没有明确几何的设计变为现实。于是,最糟糕的局面出现了,施工人员无奈只能将设计图纸1/1原尺寸打印出来后,在现场切割和焊接钢板。这是一幅极具讽刺意味的画面 :一个凭借着最先进的计算机所描绘的设计最终竟然是依靠最原始的手工作业完成的。这不能不说是计算机可视化设计历史上黑暗的一幕!但问题还没结束,钢材总重量达15 200吨,折板需要通过杆件焊接来固定。但是,焊接产生的收缩变形将会导致巨大的变形应力,如何抑制变形应力成为难题。幸亏渡边邦夫四处寻找,最终在列支敦士敦觅得“喜力得(Hilti)锚栓”14,才使得问题最终获得解决。正是这种能够在钢板焊接时和钢板融合在一起的、直径仅4.5mm却可以承受高达1.5吨剪切应力的特殊锚栓成功地克服了钢板构件连接时的应力变形,最终将计算机的画面变为物质的形态(图4.12)。诚然计算机的形态操作可以无所不能,但是显然作为形态的建造的生产系统却并非如此。渡边邦夫由衷地说道,“如果无法找到合理的结构与合理的生产性之间整合的方式的话,那么对于设计主体的计算机而言那只能是‘No Sense’”15。
无论如何,1995年的“横滨港大桟桥国际客船站”竞赛案开启了一个“计算机可视化”的形态设计大门,它将当代计算机可视化技术与微分化的流动性通过建筑的形态展现出来。但是其中曲折的过程不禁令人深思:信息时代的虚拟技术究竟无法纵横于现实世界。计算机纵然可以无拘无束地进行形态探索,但如果仅仅是将此停留于无重力、无尺度、无建造的“三无”视屏之内的话,那结果必将是其与现实之间巨大裂缝的显现。
4.4.1 结构演算
“横滨港大桟桥国际客船站”的尴尬显然并非无解,得益于当代计算机技术的飞速发展,基于“演算”(algorithm)的形态生成显然是达成流动的结构的一种途径。
“演算”一词源于古代波斯的数学家、天文学家和地理学家花剌子密的拉丁文译名16。作为代数的创造者,花剌子密的拉丁文谐音被当作为“演算”。纳什17将“演算”的特征归纳为 :①输入 ;②输出 ;③明确性 ;④有限性 ;⑤有效性。前两项特征分别是目的和结果,后三项特征则是对中间程序运行特征的限定。一般而言,计算机的演算过程保证了后三项的特征,目的与结果则是两个对外的窗口。显然,在纯粹数理解析的年代,抽象数值将演算的过程“黑箱化”,只有输入的自我定义和输出的判明。当代的可视化解析改变了这种不透明的“黑箱化”,数值演算的过程通过图形演示的方式时刻保持了与外部身体的关联。就好比是“DOS系统”与“视窗系统”间的差异一般,“演算”不仅改变了过程的透明性,也必然导致最终形态的改变。可以说,可视化的过程是当代视觉形态呈现的根本要因。
渡边诚18将“演算”定义为“为了达到某种目的而被记录的程序”19。基于“演算”的“演算设计”(Algorithmic Design)就是“实现目的的设计行为”20。他将“演算设计”分为四个具有先后顺序的组成步骤:目的→演算→程序(program)→成果。这其中的“演算”是组合增殖的过程,“程序”可以理解为“规则”。当代的“演算设计”在计算机技术介入“演算”和“程序”之后,大量性的、复杂性的、反复性的自动生成则将“痕迹”完全排斥在外。高效、快速的特点使得“演算设计”成为获取“最适解”的利器。“最适解” 是数学上的用语,指的是目的函数在制约条件下的最大化或最小化,满足这个条件的数值解被称为“最适解”。简而言之就是在“设定要求”与“环境条件”的相互整合中最优化解答。这需要在设计的全过程中对所有的有效解答进行筛选和比较。这对人类而言显然是无能为力的,但在当代计算机技术面前却是轻而易举的。
显然,排斥观念的“最适解”技术为当代设计的诸多领域大大地拓展了可能。特别是近二十年间将“演算设计”的“最适解”导入航空及汽车领域后在空气动力学和材料轻量化方面的成就备受瞩目。此外在交通、金融、智能化等各个涉及复杂系统的领域中,“最适解”的出现无疑使各行各业都能够分享到在社会性、经济性和使用性方面最完善的产品。那么,是否在建筑形态中存在着这样仅需判断就可以作为设计的“最适解”呢?或者说建筑设计的行为是否可以被程序化所取代呢?现阶段在建筑设计领域依然只是缓步前行的“演算设计”显然并不是一种消积的回应。这是因为建筑物不同于机械产品,首先,在单品建造与大量标准化生产上的不同,使建筑除了在坚固性和轻量化的量化指标之外,还与施工性、经济性、社会性、舒适性、审美要求等相关,而这其中并非每一项都是量化的指标。其次,建筑还与特定的风土、文化、物理环境相关,仅仅是几个单项上的“最适解”显然无法应对量化困难以及变量过多的建筑设计的特征,这就使得“演算设计”中的“最适解”无法通过建筑设计来获取,进而也意味着程序无法取代思考。尽管如此,并非“演算设计”在当代的建筑形态设计中毫无用武之地。事实上,“演算设计”可以分为两类,一类是以正解应该存在为前提进行搜索的组合,另一类是以搜索大致上正确为目的的组合,后者也被称为“启发式设计”(Heuristic Design)。与没有正解就被完全排除的两分法不同的是,以“大致正确”为目标,不断靠近前行的“启发式设计”对于设计行为而言正是这个世界的本来面貌。设计中不存在绝对的唯一解,却也并非随机,“大致正确”的解的意义在于它为计算机与身体之间意志的介入留下了余地。模糊与暧昧、境界的混合与交换,这些都是当代性关系的显现。不得不承认,当代的计算机技术正在改变我们的思考方式,这一点对于建筑设计而言也是一样的。“演算设计”的改良化筛选可以使建筑设计在某些量化的指标上进行改良范围的圈定,比如经济性和轻量化的优化。这些解答虽然对于整个建筑设计而言并不是独一无二的“最适解”,但却是改良建筑整体性能的“优化解”。“优化解”的选取依靠的是人类根据经验、能力和具体条件作出的附加判断。这就如同是“大分县立大分图书馆”设计中身体介入瞬间的“切断”。“切断”意味着“决定”,甚至被等同于“设计”,身体的主体性显然让渡给了计算机,价值存在于判断的那一瞬间。
佐佐木睦朗将结构通过计算确定形状的方式称为“顺解析”,那么结构演算形态则将“顺解析”的过程倒置为“逆解析”——形态设计的过程(图4.13)。他将原来的结构设计方式称为“经验的手法”,结构的演算设计称为“数理的手法”,两者“设计形态”的统合方式显然是不同的,“经验的手法”是依靠经验,即主观的观念来统合(型式的选择)的,而“数理的手法”则是通过计算机的设计解析(演算的逆解析)来获得结果的。结构在设计形态被观念确定后的调整自由度与从一开始就参与形态建构的自由度是无法相提并论的。因此,结构演算的形态设计显然极大地提高了计算机技术在形态生成中的参与度。
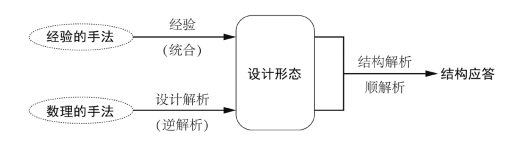
图4.13 形态设计的过程与应答过程
4.4.2 感度解析法
在当代的结构设计中,具有自由、复杂、不定形、流动、有机特征的新三维建筑结构的创造,使建筑挣脱了近代以来的束缚,在不断扩大建筑的领域之际,也正在成为国际化的当代主题。不过,要将此当真以合理的方式实现,替代原来经验式的结构设计手法,统合力学(理性)与美学(感性)的数理形态设计手法就成为必要。21
我所提倡的形态设计手法中包括了感度解析手法和进化论的结构最适手法。这是将生物的进化及自我组织化等原理以工学的视点加以捕捉,然后通过计算机来对合理的结构形态进行创造。现在,为了使这些手法能够更加适用,我们正在对上述的这些新建筑结构进行不断的尝试。其应用的实例之一是自由曲面结构,另一个例子是流体结构。
与之前传统的顺解析相比,佐佐木睦朗将计算机的图形演示能力引入到结构的解析之中,形成了具有当代性的可视化解析过程(表4.4)。以原始茅屋线性的木架构形成的支撑体系与以洞穴为代表的连续面覆盖体系这两类结构起源在当代的结构演算形态中依然被佐佐木分成为相对的两种类型 :作为支撑体系的流体结构和作为覆盖体系的自由曲面结构——感度解析法,并且这两种类型也基本涵盖了日本当代建筑中的计算机结构演算的所有形态。
表4.4 感度解析法结构形态比较
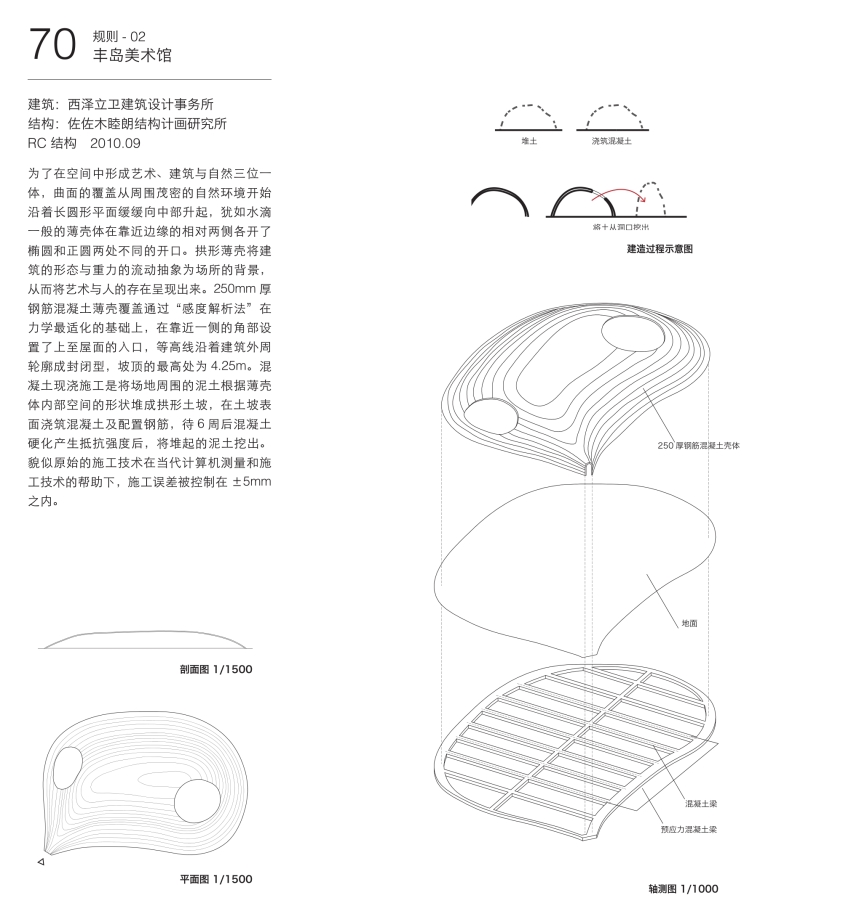
通过计算机可视化解析的自由曲面结构来对覆盖基进行表现的最初尝试是1998年佐佐木睦朗与矶崎新合作的“中国国家大剧院竞赛设计方案”。150mm×225m的自由曲面混合薄壳屋面由下部建筑内部的剧场、各种多功能厅、光庭以及外周的列柱支撑。曲面结构屋面分别由结构和下部功能空间对高度的要求两部分共同控制。为了更好地控制曲面结构的变化,首先需要对曲面形状进行坐标化。一般的有限元法就是通过对不同的坐标点的结构应变值进行数值解析,反复调整各坐标点的空间相位位置以及与解析演算的结合来对形态进行收束,逐渐使各坐标点的应变强度与使用要求符合力学与空间的双重要求(图4.14)。不过,像这样反复试错的调整与解析过程是需要付出极为大量的时间和人力的。其原因归根结底还是因为这种曲面坐标的调整与结构验算的设计行为还是停留在从设计到解析的顺解析阶段。随着计算机技术的飞速发展,在2000年之后,以力学数理解析为基础的计算机结构演算设计的应用开始变为可能。这就是被称为“感度解析法”的计算机结构演算下的自由曲面形态生成方法。其基本的演算规则是基于对于形态抵抗型的空间薄壳结构而言,应力与变形越小,结构物的应变也越小,相应的力学性能也越好。反过来说就是通过使结构物的应变最小化而获得的曲面形态是力学上最适化的薄壳形态。其基本方程式如下 :

图4.14 中国国家大剧院竞赛设计方案

在这一方程式中,基准应变值被微分为设计变量。比如在将某个节点稍许变化时,其对整个结构物所产生的影响可以通过应变量C的变化察知。表示这种变化程度的微分系数在力学上称为“感度系数”,这是“感度解析法”得名的由来。对所有节点处的感度系数进行求解,就可以获得应变量变化的趋势,从而对由应变变大或减小所带来的的影响作出判断,以最适化的方针对控制应变值的设计变量Z值给予修正。此时,当某节点处的感度系数为正的话,则可以将Z值减小,反之为负的话,则可以增加Z值的大小。由此通过计算机对这样的参数值的控制,以有限元法的反复计算来逐渐实现应变量趋小化的曲面形态。形态收束的判定依据是以应变演化不再发展为准。这样的曲面形态演化过程可以通过计算机“即视化”的图形演示方式分步呈现给判定者。它将数理方程式的“暗箱化”解析变为可视化的透明过程。
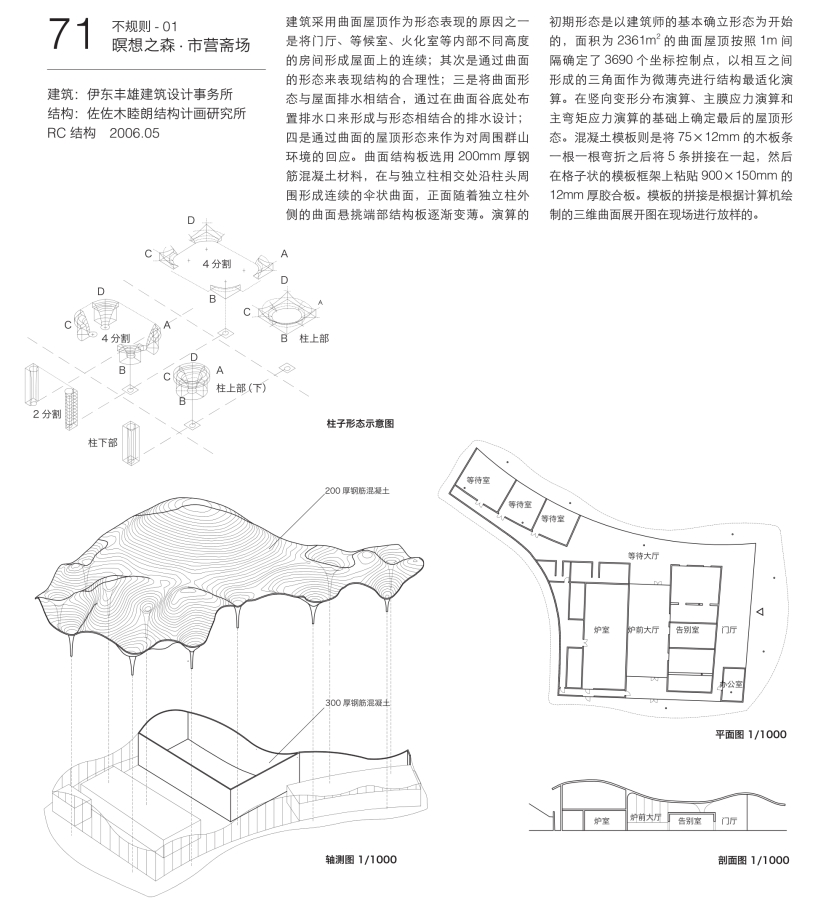
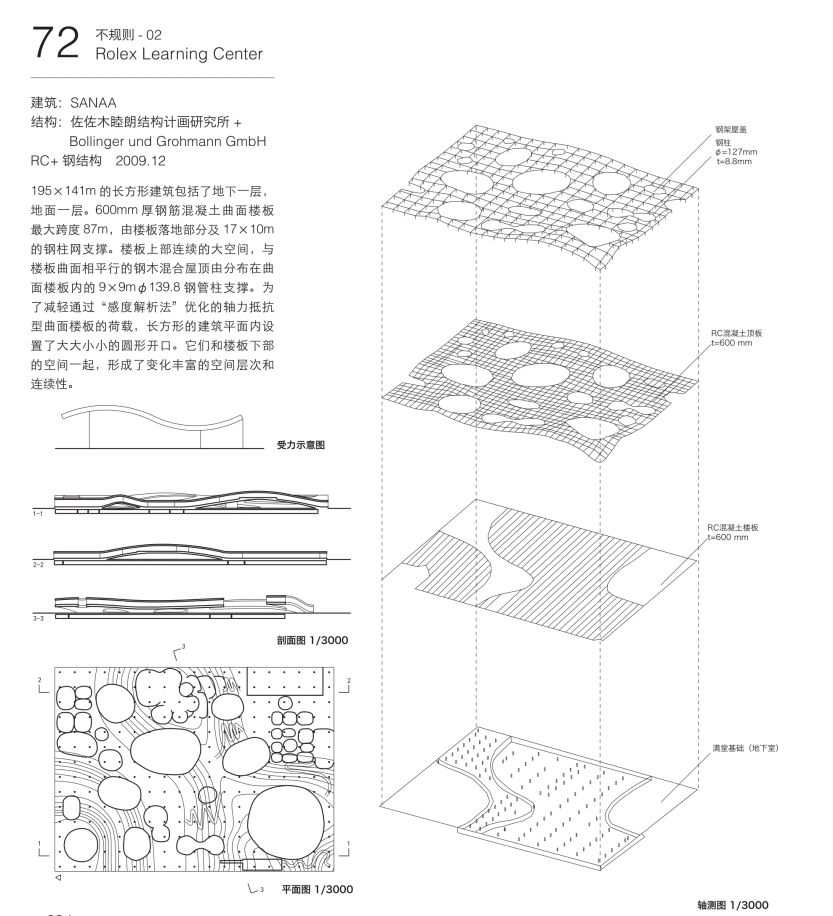
以简单平板为例来说明这一曲面形态演算的过程。周边支撑的5cm厚、50m见方的平板,在每平方米承受1吨竖向荷载时的结构最适化变形过程中,首先在变形初期对平板指示向上部凸起的方向命令。由此,接下去计算机会根据应变最小化的演算规则对平板进行上凸化变形。当这一变形进行到第40步时可以确认板内的应力呈均质分布,但也造成了原先平板的表面积大幅增加以及曲面结构高度过高等不利结果。由此可知结构本身的最适解并非是建筑形态上的最适解。从第40步向前倒推,可以发现在第25步时,结构的应变状态与表面积和高度的整体平衡最为理想。然后是对平板进行振动模式下的1次到3次模式下的初期形态设定,并查看各自不同的形态演算结果。凸状的1次振动模式从初期状态到最后安定形态,其应变量非常小,产生了以压应力为主的高刚性稳定形态。而当其面对2次模式和3次模式时,进而又产生了剧烈的凹凸演化,朝向复杂的曲面形态变化。与1次模式的形态相比,结构内除了压应力之外,还包括了张拉应力和弯曲应力的混合,相应的应变量和变形也趋大,刚度下降。从横轴演化的步骤以及纵轴应变量的变化可以看出不同模式下清晰的演化变形趋向。由此获得曲面形态也同时明确了结构的空间位置坐标,接下去通过NASTRAN等常见的有限元法软件根据结构的坐标点进行进一步的数理顺解析,以此来对确定的曲面结构物的力学状况、应力、变形等进行验算(图4.15,图4.16,图4.17)。
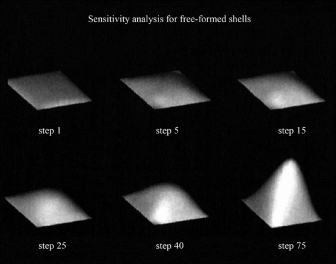
图4.15 50m见方平板模型
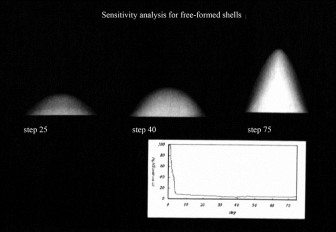
图4.16 5cm平板模型

图4.17 平板模型的振动试验(从上往下a 、b 、c 、d )
4.4.3 扩张ESO法
与“感度解析法”一样,流体结构也是基于计算机可视化解析的结构形态。其得名源自于对植物重力抵抗机制的发现。同先前结构表现主义如弗雷、渡边邦夫对植物形态抵抗重力的结构模仿不同,佐佐木睦朗将植物令人难以置信的环境适应能力以及自我组织化的生物学本质作为力学形态生成的原理。比如亚热带植物悦榕树在几乎倾倒的树干处总能发现数根支柱支撑,这是其在倾斜之中从自己的主干分叉而出的侧枝。这些从主干分出的悬挑侧枝,在针叶林与阔叶林之间存在着很大的差异。阔叶林总是要么下端膨大,要么上端膨大来形成结构上的补强。在悬挑伸出的侧枝根部形成较大的截面使应力均质分布的应力抵抗原理是植物在自身演化历史中形成的自然规律,这被认为是生物自我组化能力的重要原则。像这样当材料的强度一定时,通过截面的增减来形成均质分布的应力原理,在建筑的结构上也是一种非常经济与合理的方式。从这些亚热带植物的形态进化中我们可以看到,无论面对怎样的力学环境,一种激发植物生命力的激素在强有力地支撑着它们以各种形态成长。而基于这种植物形态机制的力学原理就是作为流体结构的“ESO法”(Evolutionary Structural Optimization)。这是由谢亿民22于1997年提出的基于消减掉结构物中力学效应较低的部分,然后在剩余的部分中进行应力的重新分配之后,再重复地进行消减与分配的程序;是在反复的消减与重分配的操作下,结构物形态被逐渐导向效率最佳的一种结构最适化方法。结构破坏一般是由应力和应变过大导致的,同时也存在着效应指标过低的抵抗应力和应变。理想的结构状态应该是像植物的枝干那样,所有的结构物部分均布地承担接近于安全范围附近的应力。ESO法就是将此原理作为演算的目标的。
不过,由于ESO法只是通过单方向地消减材料来达到应力均布的目的,其结果会使形态不断地变得更细。将结构物的形状在消减低效部分的同时,在必要的部分通过增加材料来获得均布结构形态的方法被称为“扩张ESO法”,它是在2004年由崔昌禹、大森博司和佐佐木睦朗在“基于扩张ESO法的结构形态创生——向三维形态扩张”23的论文中提出的。其与ESO法相比具有两点不同 :等价线(三维上的等价面)的导入及消减部分的复活增长可能的双向进化。扩张ESO法的过程包括以下5个步骤 :
第1步,将要进行最适化的设计区域进行要素分割 ;
第2步,根据所给予的荷载条件、支撑条件,通过有限元法对结构进行解析,对各要素进行定量计算 ;
第3步,将设计的整个区域点阵化,以确定消减的基准值并由此形成等价线 ;
第4步,沿等价线消减材料,形成下一循环的设计区域 ;
第5步,重复上述第1—4步,直到达到最终进化目标或基准量达到限定值为止。
通过以上的非线性形态解析的反复,结构形态与结构物的力学性能在联动的状态下形成整体上的有机结构形态。也由此可以获得弯矩被最小化,且应力基本处处相等的应力抵抗状态。通过扩张ESO法与ESO法在同样初始形态下演算过程与结果的比较,我们就能非常清晰地看出前者的优异性(图4.18)。首先扩张ESO通过双向进化可以对既有形状进行修补,以获得更加有力的应力分布,并使等价线的确定具有更大的自由度,形态的进化更加有利。同样高度、跨度及面积的结构物,ESO法进化的最适化结果是桁架,而扩张ESO则是材料与受力更加完美的“镜框拱”(Suspend Arch,图4.19),甚至它以同样跨度与高度的结构物进行演算可以获得与罗伯特∙ 马亚尔(Robert Maillart)241930年设计的著名的塞吉那托贝尔桥(Salginatobel Bridge, 1929,图4.20,图4.21)一样的结构形态。事实上,大跨度桥梁中无论是张拉型的吊桥还是压缩型的拱桥都是尽量将弯矩应力最小化的均布应力结构,只有在这样的情况下才有可能实现最轻量化的大跨结构。

图4.18 扩张ESO与ESO的区别

图4.19 扩张ESO与ESO跨度演算比较

图4.20 桥的最适化过程

图4.21 塞吉那托贝尔桥(Salginatobel Bridge)
我们以一个佐佐木睦朗对结构形态的演算例子来说明扩张ESO法的生成过程。初始形态的设计区域为短边处沿宽度方向设置对称两端各两个间距10m的支点所支撑的宽36m,高15m,长150m的长方形平板。建筑上的限制条件是屋顶的上部是平的,中央部分的下侧距屋顶距离在12m之内。所使用的结构材料是钢结构,荷载条件设定为屋面均布竖向荷载w=1t/m2。从扩张ESO法演算图形过程可以看出,从初期状态开始,首先是两端的支柱处由于巨大的竖向荷载使得柱子截面变粗,之后屋面平板应力较大的部分也相继变厚,进而与开始倾斜的两端支柱形成拱形连续。其后是在屋面板的中部发生形态突变,将下部抛物形状的支撑构件与面板分离,从而使整体成为以轴向抵抗为主的结构形态。此时演算形成的结构宛如一个放大的连续梁受弯应力分布的拟态形式。接下去,向上部延伸的拱形与向上部伸展的抛物形的相互连续进一步演化,与此同时为了降低屋面板结构的复合应力,也就是作为整体结构上弦内轴向应力与部分板内的弯曲应力,在靠近拱形与抛物形的一部分相接处继续产生分叉变化。其中抛物形构件靠近平板的原因是由于支撑结构被限定在距离屋面12m之内初始设定的缘故。在演化的最终阶段,结构形态的局部形状通过细微的演化后,形成了满足设定条件要求下的整体结构中弯曲应变量最小化,基准应力沿结构全区域内基本均布的结构形态。可以说这一形态将作为目标设定的荷载以最高效的方式传递,是力学范畴内最为经济的合理形态(图4.22)。
这一ESO扩张法的演算过程也是佐佐木睦朗与矶崎新合作的“佛罗伦萨新站竞赛案”形态设计的过程。其比上述示例的平板屋顶面积更大,是一个长400m,宽40m,高20m的巨大流体结构形态(图4.23)。下部由两排各四处筒体空间作为支撑。为了简化对屋面扩张ESO法的演算,将屋面按照长向对称分为左右两部分,然后先对其中的一侧进行形态优化演算,作为另一侧的参考,进而将两处屋面拼接成一体。这是通过计算机图形计算能力来利用“人机交互”(Man Machine Interface),将力学条件与外部设计的环境变量都能够获得满足的理论解通过计算机解析,在外部设计者参数修正的反复过程中所进行的设计作业行为。审美的判断是一种无法给予定量化的指标,但是通过显示器上的图形对解析过程的表达,设计者与计算机之间终于获得了相互沟通的途径。这是当代结构可视化解析在观念与结构之间所建立起来的联系。
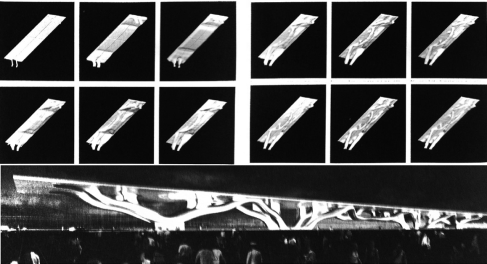
图4.22 佛罗伦萨新车站竞赛最适化过程

图4.23 a. 北京汽车博物馆方案

图4.23 b. Q Project
无论是自由曲面的覆盖屋顶还是扩张ESO的有机支撑,其混凝土浇筑模板的制作、钢筋的绑扎以及混凝土的灌注、浇捣都是非常困难的。如果说感度解析法和扩张ESO法实现了结构力学上的最适化的话,那么显然就像我们在前文中所述的那样,对于建筑而言,除了结构之外,环境的、功能的、经济的、社会的、审美的等等外因的复杂性,使得建筑形态的设计不可能存在所谓的最适解,结构最适化的形态只不过是为我们在建筑形态的设计过程中,在力学合理性方面提供了优化方向而已,它远非建筑设计或建筑存在的整个过程的最适化。佐佐木睦朗在关于可视化的形态设计所面临的课题中说道 :
现阶段的形态设计从理论上而言,尚未超越能够获取的结构力学的原理范围,事实上作为结构物的实现不可或缺的是生产技术的问题,也就是在所限定的建设费之中,合适的具体材料、连接方式、施工方法等问题依然没有解决。极端而言,形态设计就是把肆意构想形态的建筑设计以结构形态化的方式来取代,将其转变为以基于力学依据的合理化结构来作为建筑形态创造的方式,而对具体地使用什么样的材料,如何连接和建造,或是采用怎样的细部来使结构物的建造变得更加经济等这些实际的生产问题并没有真正地考虑过。不过,尽管这样的做法听上去或许是有些不负责任,但不管怎样形态设计终究是涉及结构原理问题的理论工具而已,作为暂时突破第一道关卡的理论化设计手法而言,到目前为止在我看来还是充分的。25
除此之外,我们还应该看到计算机技术下的视觉形态很大程度上受到程序演算方式的影响。换句话说,流体形态的表现类型与程序类型之间有着很大的关联,这从感度解析法和扩张ESO法各自的相似性中可见一斑。金田充弘对于当代这类由“软件”决定“表现类型”的数字化设计这样阐述道:
当下,面临着新的工具与软件不断出现而呈现出的亦喜亦忧的态势……今后,也许设计者应该对软件本身具有调整的能力吧。也就是同赋予模型以痕迹(=作为设计者的个性)相同的过程来赋予数字化以个人的痕迹。
到现在为止,人们花费在软件使用上的精力极为惊人……这也导致软件使用的门槛不断降低,其结果是“如何使用”成为胜败的关键。
“正在使用这个命令”已然等同于表现形式的决定。
目前,“软件本身如何使用”的门槛还高高在上。会使用者能够抢占到先机,但这也不过是在同等层面上的先后而已。
随着今后软件门槛的降低,我们便又将回到“如何具有独创性地来驾驭软件”这一原先的评价体系上来。26
原本设计者的个性化和多样性在程序运算规则的制约中显然被抹杀,形态的差异转化为程序的差异。这一现象也是流体形态表现给我们的提示,如何在可视化设计中表现原有的设计师个性化势必将会成为下一步计算机设计程序进化的方向。