4.2.2 数学建模
4.2.2.1 建模过程
应用能量守恒定律,着陆时动能与最初势能相等,着陆冲击速度可以计算为[8]:
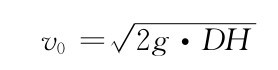
其中,v0为着陆冲击速度,g为重力加速度。根据动量守恒定律,可以得到:
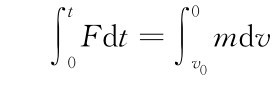
其中,F为作用在单腿上的竖直方向合力。当t=0,即初始接触时刻,v=v0。着陆冲击过程中,F为时间(t)的连续函数。根据中值定理,会有F′,满足F′Δt=mv0。则:
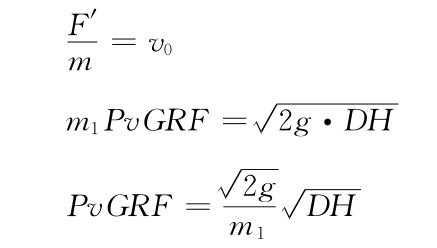
其中m1为修正参数。因此,Pv GRF和DH的关系可以推导为平方差形式。在冲击过程的最后,即受试者达到稳定状态时,F值为体重的一半(BW/2),而不是0。因此,另外一个参数需要被代入到这个公式中,则形成了:

其中a~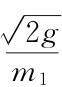 ;b~
;b~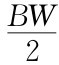 。a和b可以基于实验数据通过最大似然法得到。
。a和b可以基于实验数据通过最大似然法得到。
数学模型(4-1)用来描述双腿着陆的Pv GRF和DH的关系,非线性关系转化为线性关系,可以继而应用集成文献的数据来做回归分析。应用R语言和SPSS17.0(美国芝加哥SPSS公司)来完成统计分析。基于每个研究中的样本数和数据方差,来对R2值进行修正,来表征线性回归关系。p值小于0.05意味着可以根据自变量预测因变量。均方误差(rootmeansquarederror,RMSE)越小,意味着预测越精确。
为验证模型,采用了Mc Nitt-Gray[15]测量的一组数据的均值,在他的研究中,6名体操专业运动员和业余选手参加了着陆测试。因为实验者测量的是受试者双腿受力,所以这组数据并未被包括在系统综述(评价)的集成数据中。此外,用该数据来做验证,主要原因还在于:测试为严格控制的双腿着陆,与系统综述(评价)中的其他标准完全符合;测试的DH为128cm,超出集成数据集中的最大值(103cm)。
4.2.2.2 平方根线性拟合
针对3种等级频率的回归结果如图4-3所示。对低频、中频和高频,3个回归的RMSE分别为0.83、0.37和0.46,对应的修正R2值分别为0.73、0.94和0.46,所有p值小于0.001。方差分析显示,3个回归方程的a值有统计学差异(p<0.001),而b值无显著性差异(p=0.35),b值得加权平均值为0.34。
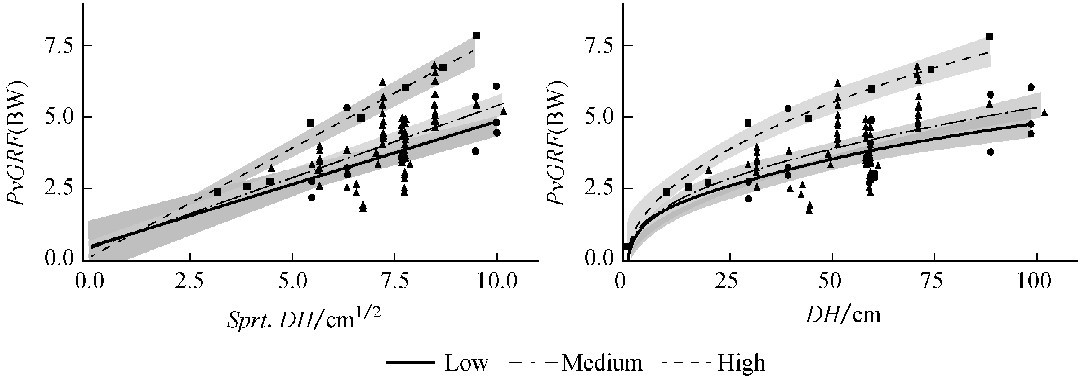
图4-3 跳落高度(Dropheight,DH)的平方根和竖直方向地面反力峰值(peakvertical groundreactionforce,Pv GRF)关系回归分析。低频:Pv GRF=0.44 +0.45 (RMSE=0.83,Adjusted R2=0.73,p<0.001);中频:Pv GRF=0.49
+0.45 (RMSE=0.83,Adjusted R2=0.73,p<0.001);中频:Pv GRF=0.49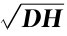 +0.37(RMSE=0.94,Adjusted R2=0.45,p<0.001);高频:Pv GRF=0.75
+0.37(RMSE=0.94,Adjusted R2=0.45,p<0.001);高频:Pv GRF=0.75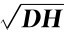 +0.17(RMSE=0.46,Adjusted R2=0.96,p<0.001)。
+0.17(RMSE=0.46,Adjusted R2=0.96,p<0.001)。
采用Mc Nitt-Gray[15]测试的DH=128cm时的数据来验证回归模型。因为该研究中采样频率为1000Hz,所以验证的模型为中频回归结果(Pv GRF=0.49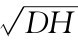 +0.37)。如图4-4所示,根据回归方程预测, DH=128cm时,Pv GRF=5.9BW。
+0.37)。如图4-4所示,根据回归方程预测, DH=128cm时,Pv GRF=5.9BW。
4.2.2.3 平方根公式的优势
Yeow等人[10]曾经采用简单线性、指数函数和对数函数去拟合实验测量地面反力峰值和DH的关系,最后比较发现最好的形式为指数函数:
y=aebx
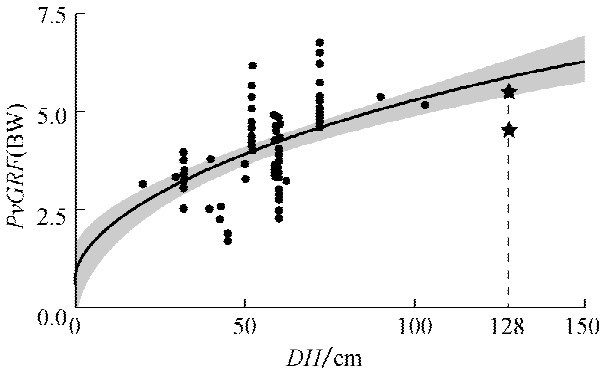
图4-4 回归方程的验证。两个星型符号表示Mc Nitt-Gray[13]文献中实验测量的128cm高度跳落时测量的竖直方向地面反力峰值。阴影部分表示95%置信区间。[17]
其中y=GRF,x=DH。这个指数函数的拟合是基于个体数据,即每名受试者从不同高度跳落着陆时的数据进行分析,不同受试者之间的公式差别非常大,因此对其他研究者没有指导意义。而本研究中的平方差公式是基于严谨的理论分析和系统综述(评价)的大样本数据获得的,具有普适性,其他研究可以直接借用过去。
这个指数函数拟合仅仅出于数学的考虑,而未考虑其实际意义。例如,在临界状态零高度(x=0)时,该函数得到结果y=a。其研究中回归系数a的范围介于1.19和1.52之间。这也就意味着,当受试者双腿站立在水平地面时,其单腿承重将达到1.19~1.52 BW! 这是难以合理解释的。而在本研究的平方差公式中,当DH=0时,Pv GRF=b。根据我们的研究结果,截距b在大多数情况下均处于合理的区间内。
即使从数学考虑的角度,指数函数也并不尽如人意。例如,指数函数的定义域为整个有理数区间,即从着陆高度的选择可以遍历-∞到+∞,但是,我们是无法设想一个人是如何从高度为负数的地方着陆于地面的。而在本研究的平方差公式中,定义域被限制为不能为负数,这就明显更加容易解释。
本研究剔除的平方根函数公式,还被其他文献中的实测数据进行了验证。在用来做验证的文献中,Mc Nitt-Gray[15]测量的Pv GRF为双足受力,两组受试者的均值分别为11.0BW和9.1BW。基于我们之前提出的猜想[20],双足着陆时双腿为不完美的同时触地,因此,作用在单腿上的最大冲击力应该略大于双腿合力的一半。因此,可以认为本研究结果很好地得到实验结果的验证。
