5.1.3 Any Body软件
5.1.3.1 简介
Any Body是针对于肌骨系统逆向动力学的分析软件。Any Body Modeling System有其自己的编写语言Anyscript,可以分类编写人体肌骨系统的各个节段,根据这些数据和内部的算法,通过软件可以计算出各个关节和肌肉的作用力。
Any Body中的刚体节段并没有特定的形状(软件中默认显示为椭球体),而是以质心位置和惯性张量来定义的。软件中刚体节段的重要特性是,一个刚体节段可以有多个节点,从而为关节以及肌肉的定义提供标识点。Any Body中的关节可以理解为对刚体节段相对位置的束缚,减少刚体节段运动的自由度。另外,Any Body中提供了多种关节模式。
Any Body软件对肌肉的建模分为两大部分:一部分是以肌肉的形态和运动学状态来建模,即对肌肉的位置、连接路径建模;另一部分是以肌肉的强度建模即对肌肉的简化工作原理建模,包括定义肌肉的简化模型及其相应的参数。根据肌肉的形态,Any Body中主要有两种肌肉模型:一种是由肌肉起止点和一些刚体上的肌肉经过点来定义的肌肉,肌肉的起止点很重要,因为肌肉固定于起止点上,肌肉力则在这样的方向传递;另一种是包裹型的肌肉,这样的肌肉也需要起止点。然而不像第一种肌肉在起止点之间有内部的连接点,包裹型肌肉则越过刚体的一个或多个表面,肌肉与骨之间的接触力垂直于骨表面。
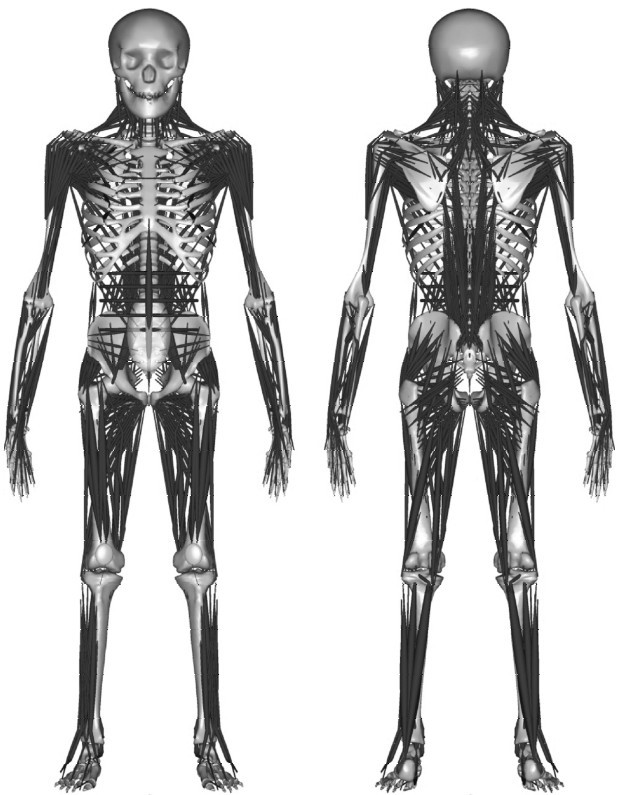
图5-1 Any Body Modeling System人体模型[10]
对肌肉工作模型的描述主要有以下两种:
(1)基于希尔经典研究的满足肌肉工作现象要求的模型。这类模型都将肌肉简化为一些收缩元素和弹性元素,它们不去探讨肌肉收缩的微观原理,而是直接关注收缩的属性,该类肌肉具有良好的运算性。
(2)基于赫胥黎对于肌肉收缩时跨桥活动这一微观物理现象研究的模型。这类模型将肌肉收缩简化为一系列微分方程,解该类肌肉的活动性需要较大的运算量。
逆向动力学分析的关键问题在于,通过平衡外界载荷得到各个肌肉的受力情况,通过等式Cf=d(f为肌肉、关节受力,C为肌肉系数矩阵,d为外界载荷),可以得到一系列线性方程。线性方程组很容易求解,然而肌骨系统的逆向动力学分析并不那么容易,主要原因有两点:①肌肉是单方向的,只能拉不能压,因此肌肉力的符号是确定的,只能为正或者为零;②肌肉冗余问题,肌骨系统的肌肉数量远远大于平衡外部载荷所必须的肌肉数。
逆向动力学中,肌肉相互协调配合的机制其实是优化问题的方案设计,即基于以下等式的优化问题:
Minimize G(f(M))(5-1)
Cf=d(5-2)
0≤f(M)i ≤Ni,i∈{1,…,n(M)} (5-3)
G是一个客观的函数,为假定的神经中枢系统对肌肉受力的分配策略,以肌肉受力f(M)为应变量。考虑到所有未知力f、G要最小化,其中f=[f(M)Tf(R)T]T,f(M)为肌肉力,f(R)为关节力。等式(5-2)是动力学平衡方程,是优化算法的限制条件。C是未知力的系数矩阵,d包括所有已知的应用加载和惯性力。肌肉力的非负数限制表明,肌肉只能承受拉力,上限值限制了肌肉的最大受力,Ni是肌肉的强度。
常用的客观函数G是多项式,还有不太常用的函数形式,如“软饱和准则”(Soft saturationcriteria),其体现形式为:
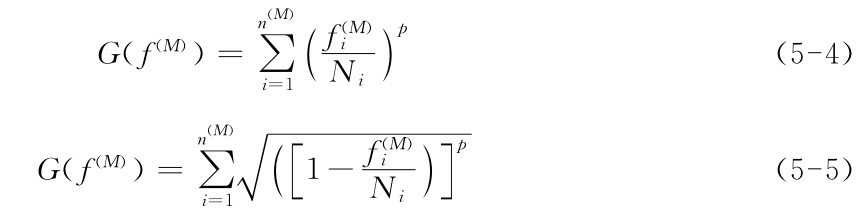
这两种形式的G函数都有级数p,和对每一个肌肉的标准化函数Ni。标准化的肌肉力通常指肌肉活动性。从生理角度讲,Ni最合理的选择应该是对肌肉强度的测量,可以将其近似成常数也可以是将肌肉作用情况综合考虑的模型计算结果。
还有一种肌肉配合优化方案,称为“最小最大准则”:

该准则是使最大肌肉活动性为最小的优化准则。这一优化准则的很多特性使其相对于软饱和准则更有优势。
首先最小最大准则可以转化为线性问题,计算效率高,可以用有限的算法解决问题。软饱和准则在p=1的时候也有相同的特性,但是p=1时软饱和准则与人体生理实际现象不符,这样的计算结果会使强度大的肌肉完全承担所有承载,而事实上所有的肌肉都会分担承载。
当级数p变大时,软饱和准则的计算效率会降低,而且多项式准则必须要有肌肉受力上限(5-3),而软饱和准则和最小最大准则将这些限制包含在其形式表达的各自等式中,在第二大受力的肌肉的运算中即可进行处理。软饱和准则在肌肉受力接近上限值时会引起计算的失效,而最小最大准则会简单合理地分配肌肉力,肌肉受力不会超过上限值。这种控制上限的方法也使得最小最大准则具有更大优势。随着级数p增大,软饱和准则倾向于接近最小最大准则的计算结果。另外,当p为较大数时,肌肉活动性与外部承载力的关系接近于线性函数,而最小最大准则本身就是线性关系。发现当级数p非常大时(p=100),其计算结果与采用最小最大准则所得到的结果相一致。
除了计算上的优势,从生理学角度来看最小最大准则也是很有优势的。假设肌肉疲劳与活动性成正比,这一准则可以尽可能地延迟肌肉的疲劳程度,也就是说这一准则是最小疲劳准则。基于以上的讨论,最小最大准则已经成为Any Body软件逆向动力学分析的基础。但是在生理学上,并尚未有严格的实验证明,以上各种优化准则哪一个更有优势。
一些研究者认为最小最大准则造成了过多的肌肉协调,使得肌肉的工作状态恶劣,如力矩很小。最小最大准则对于非最大承载肌肉的活动性计算有不确定性。这一问题的解决还需要软饱和准则提供确切的迭代方案,使得在Any Body计算过程中肌肉活动性、肌肉受力的求解能最终确定下来。
机械系统的数学模型必须满足运动等式(5-2),模型采用多刚体动力学系统方法,使用每一个刚体的笛卡尔坐标系。这是进行高效运动学分析的易于执行的选择。这一选择的合理性在于,运动学只是分析的一小部分,我们需要处理的肌肉数目远大于刚体数量。所有生物力学系统的节段都被建立为刚体,忽视软组织摆动的影响。第i个刚体的位置描述为qi=[r Tip Ti]T,其中ri为质量中心的全局坐标向量,pi为包含四个欧拉参数的向量。刚体速度定义为vi=[(r·Tiw′Ti],W′i是刚体自身坐标系衡量的角速度。
动力学分析都在笛卡尔坐标系下进行,解方程组:
φ(q,t)=0(5-7)
q=[q Ti…q Tn]T共为n个节段,时间t表示除了正常关节的整体限制,一些运动学的限制正是运动的驱动因素。在逆向动力学分析中,这些限制要将运动完全确定下来,也就是说方程组(5-7)需要完整地包含n个节段的信息。我们也需要包括对欧拉参数的统一限制。方程组(5-7)基本上是非线性系统等式,使用修正的牛顿拉夫逊方法求解。
接下来,求解线性速度和加速度,用以下方程,用v和v·而不是q的时间导数:

φq*是q*的雅可比限制,q*包含与v相关的模拟位置,它作为由于v旋转而产生的有限值是没有意义的,但是作为微分的极小值是有意义的。
目前,我们已经知道了关于运动的q、v和v·,故可建立动力学等式。对每一个节段,有牛顿 欧拉等式:
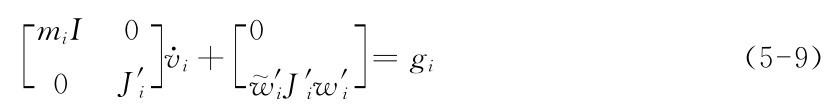
mi和j′i表示质量和惯性张量。gi为力和力矩,即以自身坐标系为参考的3个方向的力和3个方向的力矩。方程包含肌肉力g(M)i、反应力g(R)i和已知的应用加载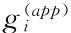 ),这些力和力矩的值取决于q,v和t。g(R)i和g(M)i相当于等式(5-2)左边,而等式(5-9)的剩余值成为di,这样等式(5-2)右边d=[d T1…d Tn]T,
),这些力和力矩的值取决于q,v和t。g(R)i和g(M)i相当于等式(5-2)左边,而等式(5-9)的剩余值成为di,这样等式(5-2)右边d=[d T1…d Tn]T,
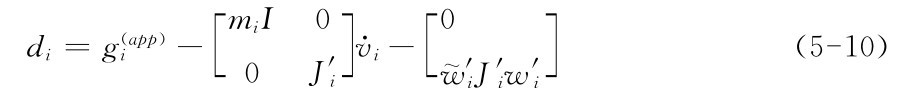
类似于未知力f=[f(M)Tf(R)T]T,系数矩阵C可以根据肌肉力和反作用力划分。C=[C(M)C(R)]定义了g(M)=C(M)f(M)和g(R)=C(R)f(R)。C(R)是移位雅可比限制φq*,这是多刚体的标准运动方程限制;f(R)是拉格朗日多项式,由外环境产生的运动学限制,对应于外界的反力,如φq*中的每一行对应于C(R)中的每一列。(5-7)、(5-8)等式中的运动学限制包括了系统自由度的运动描述。我们应该将这些运动限制排除在C(R)外,这样C(R)成为了移位雅可比φq*中的几行,与真实的力学装置相关。忽视的那些行对应于系统的自由度,由肌肉提供动力学支持。
肌肉系数矩阵C(M)需要肌肉的几何模型。我们将肌肉的几何模型当作弹簧,横跨两个或更多的点,有的也包绕在刚体上。本文只讨论横跨型肌肉而不讨论包绕型。我们可以将肌肉的起始长度写为l(oi)=|r(p)i -r(p)j|,r(p)i 和r(p)j 是横跨点的位置,由q决定。其他肌肉模型路径必须类似地提供这一长度函数l(oi)(q)和计算强度的时间导数Ni。基于虚拟工作的原则,C(M)中的系数是l(oi)的导数。首先,可以将由肌肉产生的功视为肌肉的总作用力乘以肌肉虚拟长度变化:
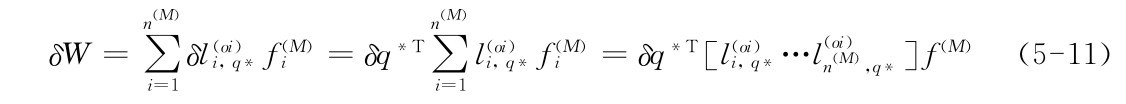
其次,我们也可以将肌肉的工作表述为所有肌肉力向量大小的变化g(M)和虚拟坐标的变化q*:
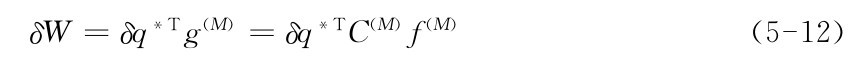
比较上两式,可以看出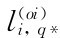 事实上就是C(M)的第i列。我们现在已经建立了肌肉作用问题的所有输入量。为了加速实际运算,可以选择性地减少平衡方程的个数。
事实上就是C(M)的第i列。我们现在已经建立了肌肉作用问题的所有输入量。为了加速实际运算,可以选择性地减少平衡方程的个数。
5.1.3.2 Any Body的应用
自Any Body软件开发完成以来,使用该软件进行逆向动力学的研究工作不断开展,其中以步态分析的研究最为典型,应用也最广。Any Body还可以用来研究不同的人体动作和人机工程的相应问题。
Damsagaard等人[10]对Any Body软件的一个步态应用实例进行了详细阐述。步态在临床上有重要的应用,步态分析对于不同疾病的诊断和康复有重要作用。假肢腿和移植体的设计都将步态情况作为衡量的重要因素,从功能角度看来,步态是唯一衡量指标。使用文献提供的研究数据,建立Any Body步态分析模型,已知数据包括下肢15个标记点的轨迹和双脚所受的地面反力,运动轨迹通过基于运动捕捉技术的摄像头记录得到,地面反力可以通过测力台测得。测力台可以捕获地面反力6个自由度的数据。这些数据足以支持分析仅包括下肢的模型。模型参数根据标记点的位置进行调整,并假设所有的标记点都连接在刚体上,忽视软组织的相关运动。由于下肢模型共有18个自由度,在测量时采用15个标记点(每个标记点三个方向的坐标值)就相对过多,其系统运动学方程属于过约束的。在实际操作中,只需手动加载18个运动学限制即可,因为大多数标记点都只记录一个坐标方向,一些标记点需要几个方向坐标的组合。通过认真选取标记点坐标值,就可以完成对运动的限定。腿部的动力学边界条件包含作用于足部的地面反力和作用于骨盆的6自由度的反作用力。由于模型不包含人体上部,因此需要加载骨盆处的反作用力。计算的肌肉活动性可以与文献测量的EMG信号进行比较。肌电信号测量结果与仿真计算的肌肉活动性结果相像,而肌肉的活动幅值却与仿真结果相差较大,值得注意的是,肌电信号幅值与真实的肌肉受力也没有确定的关系,因此肌肉活动幅值的差异不能仅仅归咎于模型的不足。测量真实的肌肉受力是非常困难的,也是不现实的,然而利用逆向动力学计算得到的肌肉活动性可以很好地反映不同肌肉之间相对的活动效率。
Saraswat等人[11]研究发现,现有肌骨模型都将足部看做是一个整体节段,忽视了足内部关节的运动,这一假设限制了模型的临床使用尤其是针对足部严重变形的案例。因此,Saraswat等人[11]用Any Body开发了三节段的足部肌骨模型,模型包括了所有包绕关节的肌肉和肌腱,并且使用经优化的肌肉路径。模型由儿科受试者的步态数据驱动,使用逆向动力学的方法计算出引起关节运动的肌肉受力和肌肉活动性。同时,模型还设计优化了每个节段的长度等参数,调整了标记点的位置,尽可能地减少由于参数及标记点位置导致的误差。最后,为了评价模型结果,将肌电信号与模型计算的肌肉活动性进行了比较,肌肉活动性与EMG测量结果十分相似。
Any Body软件除了对步态分析有重要作用外,还可用于对各种运动动作、行为进行分析。Anderson及其合作者[12]研究了脊柱承受瞬间载荷的动作,曾使用SIMM对抬举过程中的瞬间载荷动力学过程进行正向的动力学仿真,然而由于计算时间长,要将脊柱模型简化到仅含有1条肌肉进行计算。为了得到更真实的、包含多条肌肉的模型仿真,需要减少计算时间。因此,De Zee等人[13]分别在SIMM和Any Body中建立相同的两个7刚体(包含腿部和躯干上部)的二维肌骨模型,并进行了3次仿真:①正向动力学仿真,使用SIMM,起始数值为随机猜测值;②逆向动力学分析,使用Any Body软件,以抬举动作的视频分析作为输入量;③将第二步计算的肌肉活动性作为SIMM的起始数值输入寻找最佳、优化解。研究表明将逆向动力学分析得到的肌肉活动性作为正向动力学分析的起始值输入时,可以有效地减少正向动力学分析的时间。使用逆向动力学分析方法寻找合理的起始值,能使正向仿真拥有更多的细节。Holmberg和Wagenius[14]建立了双杆滑雪动作的二维模型,使用摄像机拍摄滑雪动作作为模型的输入,利用Any Body仿真计算出肌肉的活动性,虽然该模型还存在很多的缺点不足,如模型运动数据不精确、主要肌肉未加载,使得模型仿真效果不佳,但还是论证了逆向动力学分析的巨大潜力。马超等人[15]使用Any Body分析了人体在站立状态下,主要膝、髋关节的受力和股四头肌等其他主要下肢肌肉的活动性。
Wu等人[16]利用Any Body建立了食指模型,该模型包含3个指骨节段以及连接关节的7个肌肉肌腱。模型仿真结果给出了食指敲击键盘时,相关肌肉的受力情况,与近期发表的实验数据一致。利用模型仿真得到的食指肌肉活动性随时间的变化也与EMG数据一致。该模型将有助于键盘的优化设计,使指部肌肉承载较小。此外,Wu等人[16]还建立了拇指的4节段9块肌肉模型。
Any Body软件还可以用来解决人体工效学的问题。Wu等人利用Any Body软件分析了在工作场所人机工效学——踩高跷行走的动作,通过建立高跷行走的逆向动力学模型,研究这一活动对下肢关节力矩和肌骨承载的影响。在研究中,作者采集了4名志愿者高跷行走12m的数据,将这些数据输入到逆向动力学模型中,计算膝、踝、髋关节的力矩以及下肢肌群中主要肌肉的受力,将这些数据与正常行走的相应结果进行对比分析。研究表明,使用高跷行走使得膝关节伸屈方向力矩峰值增加接近20%,而踝关节跖屈力矩峰值减少15%,髋关节伸屈方向的力矩峰值也有轻微的减小,模型研究同时也得到在实验分析的下肢8块主要肌肉中5块肌肉的承载都有所增加,其中股直肌在高跷行走时的受力增加最为明显,是普通步行时受力的1.79倍。该研究深入的分析了高跷行走时关节、肌肉的受力情况,对于高跷设计的工程师有很大借鉴意义,同时使得我们对高跷行走这一动作有了进一步的认识理解。
