结构的平衡和受力分析
1.基本概念
在建筑工程中的构件和结构,是在荷载和约束反力作用下处于静止——平衡的一种,荷载和约束反力统称为外力。在对它们计算时,荷载是已知的外力,约束反力是需要根据平衡条件来确定的量。
在实际中各构件都是互相联系着的,当计算某一个构件时,首先要弄清该构件受到哪些物体的作用,也就是受到哪些力的作用,这个分析过程,称为受力分析。
把一构件从与它联系的物体中分离出来,画出用力来代替它所受到的其他物体的作用力的图形,叫做该构件的受力图。在构件的受力图上,应能清楚地反映它受到的所有的力。正确的受力分析是构件计算的关键。

2.画受力图步骤
1)明确研究对象。
2)画出作用在研究对象上的全部已知力。
3)根据各约束的性质,画出所有约束反力。
例 绘出图1-17a所示的简支梁受力图。
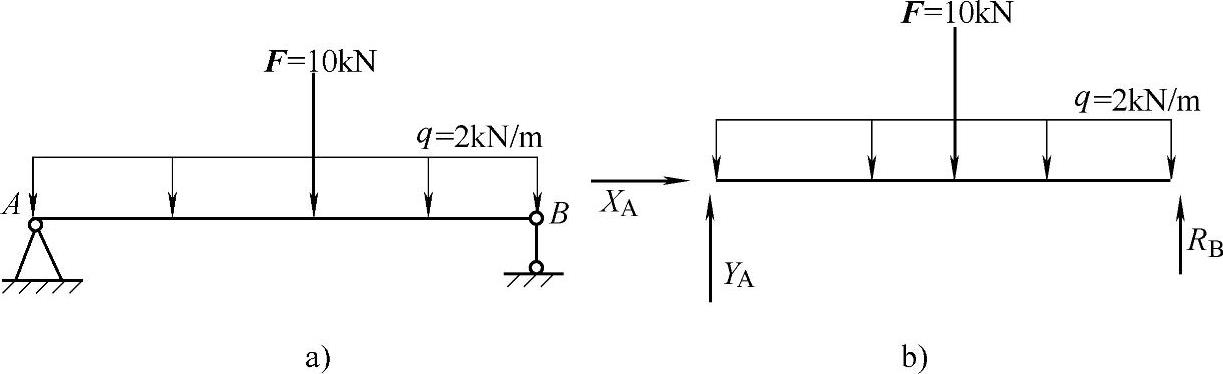
图 1-17
解 ①以简支梁AB为研究对象。
②画出作用在梁上的已知荷载q=2kN/m,F=10kN。
③受力约束反力 A端为固定铰支座,其反力可用XA,YA表示,其正确指向与主动力有关,此时可先任意假设,图中暂定XA向右,YA向上;B端是可动铰支座,其反力可用RB表示;RB应垂直于支承面,指向暂设向上。AB梁的受力图如图1-17b所示。
3.平面任意力系的平衡方程
平面任意力系的合成结果为一个主矢R′和一个主矩M′,若该力系处于平衡状态,则R′=0,M′=0。
平面任意力系的平衡方程为
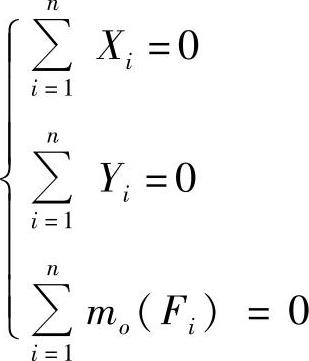
其中前两个称为投影方程,后一个称为力矩方程。它表明,平面任意力系平衡的充分和必要条件是,各力在其作用面内任选取的两坐标轴上投影的代数和分别等于零;各力对作用面内任一点力矩的代数和等于零。
例 求如图1-18a所示简支梁的支座反力。
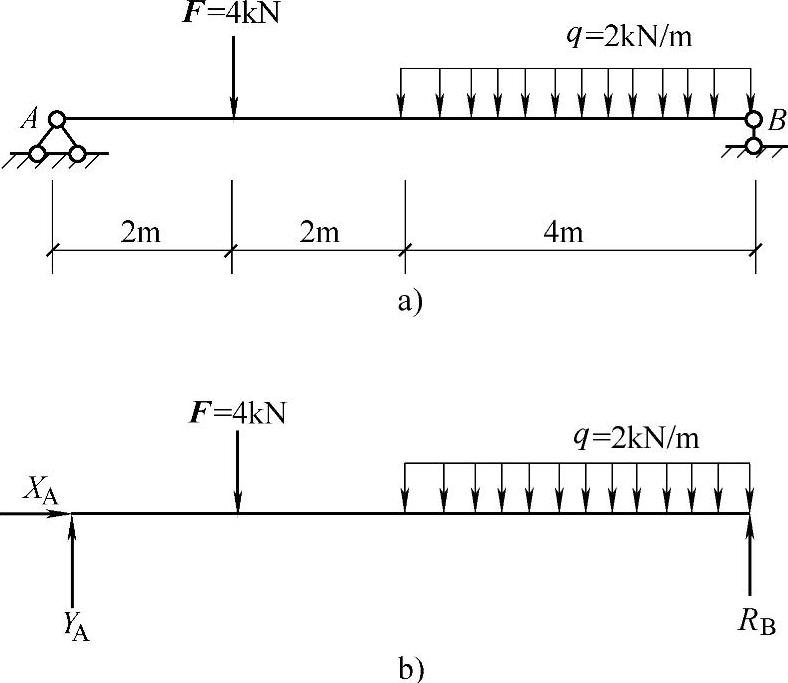
图 1-18
解 首先除去A、B两点的支座约束,并画出如图1-18b所示的受力图(其中反力指向为假设)。
根据ΣX=0,得到XA=0。
取ΣmB=0,有
YA×8-(4×6+2×4×2)=0
得到YA=5kN。
取ΣY=0,有
YA-4-2×4+YB=0
得到YB=7kN,所得YA、YB均为正值,说明两个支座反力方向均竖直向上。
