基于光照叠加的颜色恒常性计算
人类视觉系统中,视觉神经元主要通过视锥细胞与视杆细胞对不同波长的外界光刺激产生不同的响应,不同类型神经元细胞间相互作用共同形成对颜色的感知,通过神经节细胞与视觉皮层进行颜色信息的交流与传递。根据人类视觉系统对颜色的编码与传递机理,针对颜色恒常性问题,基于对场景颜色的统计信息结合图像的灰度信息,提出了一种基于光照叠加的颜色恒常计算方法,对还原物体真实的颜色信息具有重要的研究意义。图3-3为提出的基于光照叠加颜色恒常计算方法的总体框架图。首先,针对各种设备获取的外界图像或视频,不同的获取环境均会产生一定程度的色偏,本节以色偏图像(视频忽略时间维度的影响)为研究对象,记为Iinput,构建最大—均值场景光照估计(MAX-MEAN,以下简称MM估计)模型,对色偏图像的场景光照进行估计,得到MM估计后的图像IMM,计算色偏光照颜色Light1,结合图像IMM的灰度信息对其R,G,B三个通道进行分解,获得R,G,B三个通道中色偏光照颜色Light2,最后,叠加光照Light1和Light2计算颜色恒常,从而得到标准白光照射条件下的图像Ioutput。
在彩色图像成像过程中,通常使用照相机来替代观察者。因此,彩色图像成像的三个因素分别由物体、光源和照相机三个因素决定。根据Lambertian理论[22],彩色图像成像可由式(3-2)表示:
![]()
式中:x表示识别颜色像素点所在的空间位置;λ表示可见光的波长;o=[R,G,B];Ro(λ)表示相机传感器的响应函数;ρo(x)表示实际获取的图像;(t1,t2)∈T,表示可见光谱;E(λ)表示场景中光源光谱功率分布,即为色偏光照,室外场景中的光照颜色为太阳光,室内场景中的光照颜色通常为发光体的颜色;S(λ,x)表示点x位置光照的反射特性,是场景中物体表面在标准白光照射下的光谱反射率,表明物体表面真实物理属性,即为无色偏图像。
根据Lambertian反射理论,当照相机具有窄带光谱敏感度响应函数时,彩色图像的成像表达式:
![]()
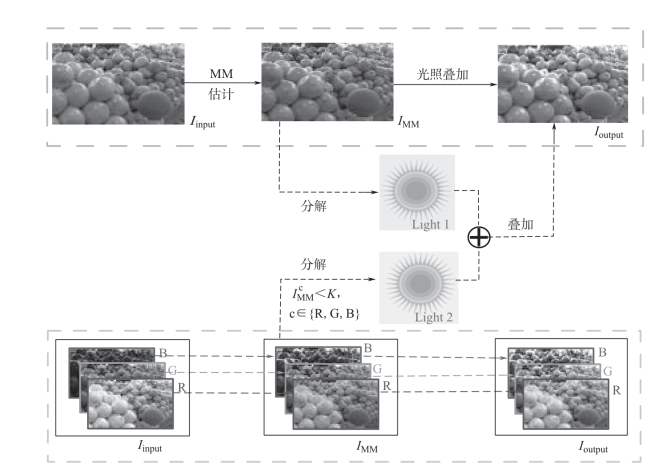
图3-3 颜色恒常计算方法框架图
颜色恒常的目的就是通过观测到的色偏图像ρ(x)估计出在标准白光照射条件下的图像S(λ,x),则式(3-3)中标准白光照射条件下的图像S(λ,x)为:
![]()
1.最大—均值场景光照估计
在均匀光照条件下,视觉系统感知的图像颜色空间中,R,G,B三个颜色通道颜色的变化相互独立,即光照对任意一个颜色通道的影响和另外两个通道无关[13]。此处采用Von kries对角变换来描述彩色图像颜色与光照的关系[14]。Von kries对角变换是一种线性映射变换,能够有效地对彩色图像进行变换,进而实现的R,G,B三个通道独立变换,将在未知光照条件下的拍摄图像转换到标准光照条件下的图像,对图像的光照进行全局修正。Von kries对角变换中,利用一个对角矩阵的变化,描述了同一物体表面在两个不同光照条件下颜色之间的关系:
![]()
式中:X=[XR,XG,XB]T表示标准光照条件下的彩色图像;Y=[YR,YG,YB]T表示未知光照条件下的彩色图像;F表示未知光照条件下获得的图像与标准光照条件下获得的图像之间的关系,F取值如下:
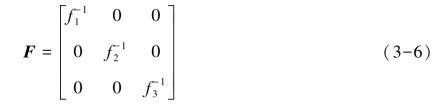
根据对角矩阵F的不同取值,得到了不同的颜色校正方法。在实际物理场景中,无色差反射即反射颜色等价于光照颜色,则针对上式中对角矩阵的![]()
![]() 和
和![]() 采用最大—均值场景光照估计,即估计场景中的所有物体表面的平均反射与物体表面的最大值反射,两者的均值是无色差的反射,则数学表达式为:
采用最大—均值场景光照估计,即估计场景中的所有物体表面的平均反射与物体表面的最大值反射,两者的均值是无色差的反射,则数学表达式为:
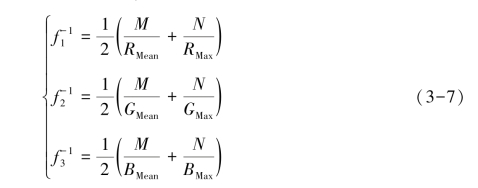 (https://www.daowen.com)
(https://www.daowen.com)
式中:M为R,G,B三个通道的总均值;RMean,GMean,BMean分为R,G,B三个通道的均值;![]() ;
;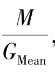
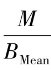 表示为物体表面颜色R,G,B三个通道平均反射;N表示标准的白光;RMax,GMax,BMax分别为R, G, B 三个通道最大值;
表示为物体表面颜色R,G,B三个通道平均反射;N表示标准的白光;RMax,GMax,BMax分别为R, G, B 三个通道最大值;![]()
![]() ;
;![]() 分别表示R, G, B 三个通道相对于标准白光的偏移量, 即物体表面的最大值反射, R, G, B 三通道的像素值范围均为[0, 255]。
分别表示R, G, B 三个通道相对于标准白光的偏移量, 即物体表面的最大值反射, R, G, B 三通道的像素值范围均为[0, 255]。
2.光照叠加物理环境中获取的彩色图像Iinput
经过MM估计得到无色偏图像IMM,以及相对应的光照Light1。有效结合图像IMM的灰度信息并对其R,G,B三个通道进行分解,获得相对应的色偏光照Light2由式(3-8)表示:式中:c∈{R,G,B},无色偏图像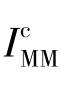 的R,G,B三个通道中像素值小于K的值(K取值为0.7),被认定为未去除干净的光照,并将图像中R,G,B三个通道中像素值小于K的均值定义为色偏光照Light2,将色偏光照Light1与色偏光照Light2叠加并对其取均值,得到新的色偏光照,从而得到最终的无色偏图像Ioutput。
的R,G,B三个通道中像素值小于K的值(K取值为0.7),被认定为未去除干净的光照,并将图像中R,G,B三个通道中像素值小于K的均值定义为色偏光照Light2,将色偏光照Light1与色偏光照Light2叠加并对其取均值,得到新的色偏光照,从而得到最终的无色偏图像Ioutput。
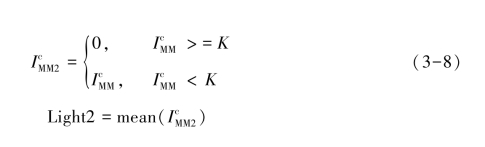
3.仿真测试
采用公开的数据集SFU Gray-ball[20],包含11346幅从视频中提取出来的4856幅室内和6490幅室外场景图像,每幅图像中有一个固定在摄像机上的灰色小球作为参考,以此获得不同场景下的光照颜色值。同时,采用常用的颜色恒常计算性能对比指标角度误差errangle作为误差度量,其计算公式为[25]:
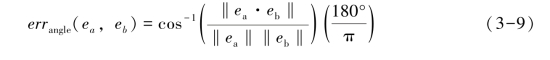
式中:ea=[Ra,Ga,Ba]T,eb=[Rb,Gb,Bb]T,ea和eb分别表示估计光照和真实光照,ea·eb表示ea和eb的点积,‖·‖表示欧几里得范数,errangle越小表明光照越接近真实光照。

图3-4 SFU Gray-ball数据集中不同光照条件下测试图
图3-4为不同光照条件下的部分测试图,(a) (b) (c) (e)为室内图像,(d)和(f)为室外图像。由图3-4中各灰色小球展示出的不同颜色可知,在不同场景下获取的图像具有不同的光照颜色。为了验证本节提出方法的有效性,针对Gray-World,White-Patch[26-27]及基于学习的方法进行实验对比(表3-1)。实验平台为Matlab R2019a,Intel Core,i7,CPU 2.60GHz。
表3-1 各种方法在SFU Gray-ball数据集上角度误差的结果对比
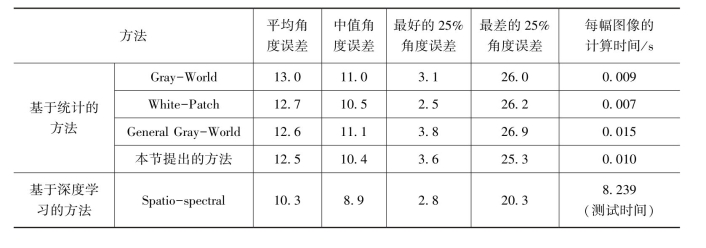
由表3-1看出,本节提出的计算方法计算效率较高,运算速度较快,相比于基于统计的计算方法,本节提出的颜色恒常性计算方法errangle较低;相比于基于学习的计算方法,本文提出的颜色恒常性计算方法运算效率较低,运算速度快。基于学习的Spatio-spectral计算方法用时为训练(64720.141s)及测试(93484.648s)总用时(158204.789s)。主观方面,针对图3-4中所列的测试图,采用上述颜色恒常计算方法进行比较,结果如图3-5所示。第一列为不同光照情况下的室内室外图像,(a)(b)(c)(e)行为室内图像;(d)(f)行为室外图像,图像中的灰色小球用来描述光照的颜色,图3-5中白色和红色虚线框勾勒出图像放大后的局部区域,清楚地展示了使用不同颜色恒常计算方法得到图像颜色的变化情况。对比(d)行图像,原始拍摄到的图像中(第一列),由于光照原因,导致远处的山体显示为较重的红色,近处的山体呈现较暗的颜色,且灰色小球用来描述图像中光照的颜色,呈现出较暗的颜色,使用本节的计算方法(第四列)与Gray-World计算方法(第二列)、White-Patch计算方法(第三列)相比较,图像左边的山体颜色更为明显,远方的山体呈现出较淡的红色,灰色小球的颜色更加明亮,更大程度上得到自然光照下的无色偏图像颜色。每一行中,通过对比图像中的灰色小球的颜色,可以清楚地观察到,本节提出的颜色恒常计算方法结果,即第四列图像中的灰色小球相较于其他列图像中的灰色小球有更清晰的颜色,表明本文提出的计算方法在可以更大程度上清除色偏光照,得到无色偏图像。上述实验结果表明,即使是在某些极端的情况下,本节提出的颜色恒常计算方法在室内和室外图像上产生较为明显的结果。

图3-5 使用各种颜色恒常计算方法和本节提出的计算方法的颜色恒常性比较
