Radon变换

Radon变换最早由数学家J.Radon提出。由于Radon变换能够较好地提取图像的纹理方向信息,因此其被广泛应用于图像处理领域的各研究方向,如图像检索、纹理检测、运动模糊长度检测以及人工智能等[51]。Radon变换即在指定方向上计算图像的投影,对于二维图像的Radon变换是在投影平面内的一组一维直线的积分,该投影平面也称Radon域(radon　domain,简称RD)。由下式定义Radon变换:

式中:f(x,y)表示二维图像;Gθ(p)在θ方向上是周期对称的,且其周期为2π;依据投影方向,p-q坐标系与x-y坐标系存在θ夹角,其中p与q可表示为:

则x与y可由式(5-6)推导:

图5-3表示二维函数f(x,y)的Radon变换[52],该二维函数可在Radon域投影为一组一维直线积分。

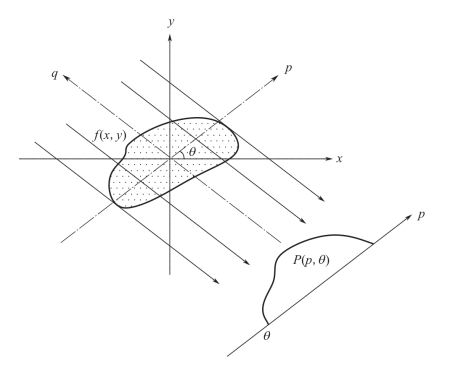
图5-3　二维Radon变换的直线积分投影表示