反应扩散方程
反应扩散方程(reaction diffusion equation,RDE)源于偏微分方程(partial differential equation,PDE)[51]。近年来,随着偏微分方程(PDE)广泛应用在图像处理领域各研究方向,进一步推升了源于PDE的反应扩散方程(RDE)的使用。偏微分方程的特点为方程式中变量与其导数同时出现,便于求解并与自然界物理量相关联,可将其扩展并用于图像处理领域以解决新的问题。
图像处理领域中基于PDE的模型,大致可分为基本迭代模型和变分模型。前者主要包括热扩散模型、正则化扩散模型、前项—后项扩散模型与扩散张量模型等,该类模型以迭代更新为基本思想,最终结果为迭代逼近式;后者主要使用一系列的变分模型,其基本思想是对能量函数求解进而获得该类模型的解。
反应扩散方程也源于PDE,其中常用的热传导方程(HCE)是一个各向同性的扩散方程,但其在扩散过程中并未考虑图像的位置信息,且过度平滑图像边缘信息影响了图像处理的质量。因此,Perona和Malik于1990年提出了PM模型,该模型在热传导方程的基础上,充分考虑图像的结构特征,采用各向异性的扩散方法,以保护图像的边缘细节信息[52-53]。PM模型可描述为:
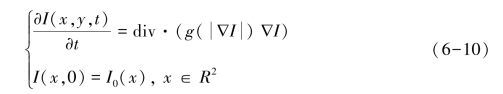
式中:I表示灰度图像,I(x,y)为图像在(x,y)∈R2处的灰度值,I(x,y,t)表示在t时刻图像处理的结果,I0为原始图像;符号∇表示梯度算子;div表示散度算子;g(|∇I|)表示扩散系数,为单调递减函数,且满足下式:
![]()
通常PM模型可预设如下两个扩散函数:
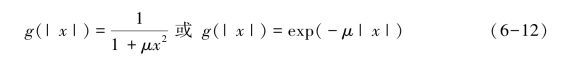
反应扩散方程(RDE)应用于图像复原的基本思想是去除图像降质因素的影响并同时保护与增强图像的细节信息。基于PM模型的RDE可描述为[62]:(https://www.daowen.com)
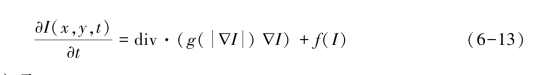
式中:f(I)为反应项。
在图像处理领域及其相关工程应用中,图像的边缘特征与细节信息包含重要的视觉特征,因此在关注复原降质图像的同时,保护图像的边缘特征与细节信息的研究同样具有重要的实用价值。将反应扩散方程(RDE)应用于降质图像复原,其在理论应用和计算性能方面具有如下特点[63]:
(1)RDE能够直接表现图像在视觉上的重要几何特征,如图像梯度、边缘切线、曲率及水平集等。
(2)RDE能够有效地模拟具有视觉特性的动态变化过程,如各项异性扩散机制、信息传输机制等。
(3)RDE能够在连续的区域中建立图像RDE模型,且在数值计算时能够使用有限差分法、边界元法、有限单元法等方法将其离散化。
(4)RDE应用于图像处理领域最重要的特点之一是可在降质图像复原过程中同时保护图像的边缘特征和细节信息。
(5)RDE能够借助PDE的相关理论对RDE模型进行分析、求解,基于RDE的算法具有计算复杂度低、稳定性好的特点。此外,PDE的黏性解理论为RDE模型提供了严格的数学理论基础。
