三、实验与分析
1.实验说明
针对本章所提出的基于结构张量—反应扩散理论的散焦模糊降质图像复原模型及算法,以Matlab7.8为测试平台完成仿真实验,选取国际通用的典型标准测试图像(包括两幅灰度图像Peppers,Mandrill与一幅彩色图像Airplane),其大小均为256×256,如图7-5所示。
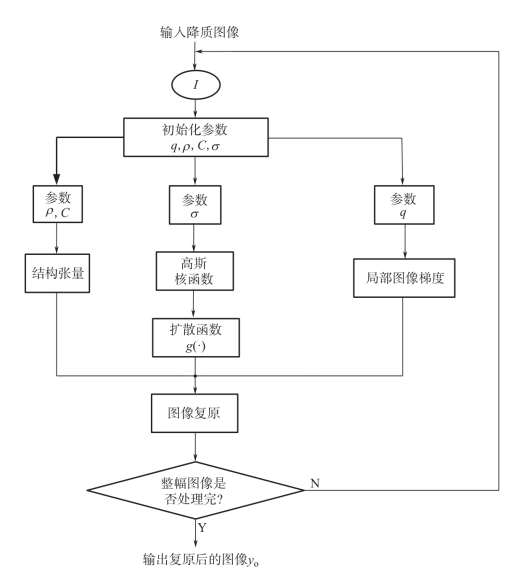
图7-4 散焦模糊降质图像复原算法的执行流程

图7-5 典型的测试图像Peppers,Mandrill及Airplane
仿真实验为量度降质图像的复原质量,采用峰值信噪比(PSNR)和噪声抑制均方误差(MSENS)来客观评价复原图像的质量。仿真实验为测评本章所提出的降质图像复原算法的有效性,将该算法STRDE与其他常见表现较好的模糊降质图像复原算法进行对比实验,这些算法包括RI-BM3D[67],BM3DDEB[67],IDDBM3D[68]及ForWaRD[70]。
2.实验结果及评价
将本章所提出的降质图像复原算法STRDE与其他常见算法(包括RI-BM3D,BM3DDEB,IDD-BM3D及ForWaRD)在图像模糊去除能力和图像细节信息保护能力方面进行性能比较。针对各类散焦模糊并附加噪声干扰影响的测试图像进行图像复原操作,给予降质图像复原质量以客观评价(包括PSNR和MSENS)与主观评价。
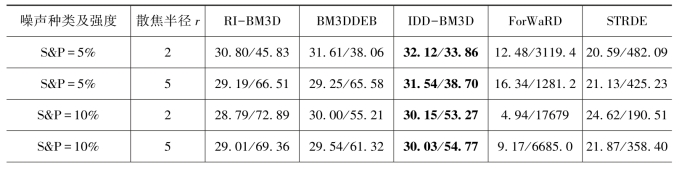
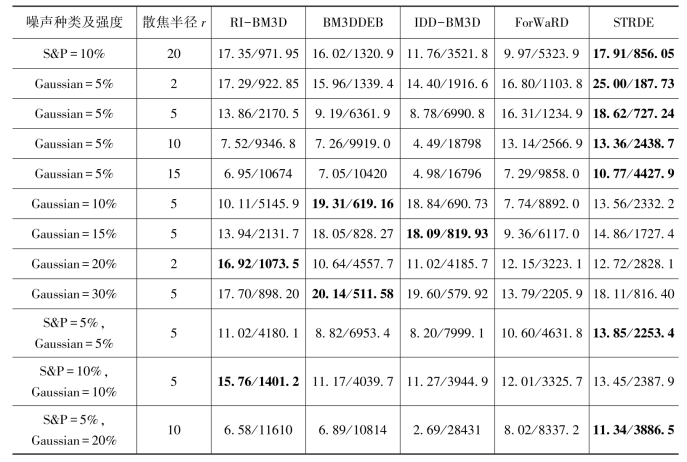
(1)图像去模糊的性能实验。对于三幅测试图像(包括Peppers,Mandrill与Airplane),受不同程度散焦模糊(其散焦半径分别为r=2,5,10,15,20)与不同强度噪声(包括高斯噪声,其强度分别为5%,10%,15%,20%;脉冲噪声,其强度分别为5%,10%,15%)影响导致其图像模糊降质,使用常见表现较好的降质图像复原算法RI-BM3D,BM3DDEB,IDD-BM3D,ForWaRD及本章所提出的算法STRDE对其进行图像复原,其复原后图像的PSNR与MSENS值被列出(表7-2~表7-4所示,且使用黑体字标记较大PSNR值与较小MSENS值。从这些列表数据获知,对于散焦模糊程度较小(其散焦半径分别为r=2,5)并附加脉冲噪声的图像,算法IDD-BM3D可取得较好的PSNR与MSENS值;对于散焦模糊程度较小(其散焦半径分别为r=10,15)并附加脉冲噪声的图像,算法BM3DDEB可取得较好的PSNR与MSENS值;对于不同程度散焦模糊并附加高斯噪声或混合噪声的图像,对比其他算法,本章所提出的算法STRDE可取得较好的PSNR与MSENS值,即散焦模糊降质图像应用算法STRDE复原后具有较好的图像质量。
表7-2 灰度图像Peppers受不同程度散焦模糊和不同噪声影降质再由不同算法将其复原后的PSNR(dB)和MSENS
续表
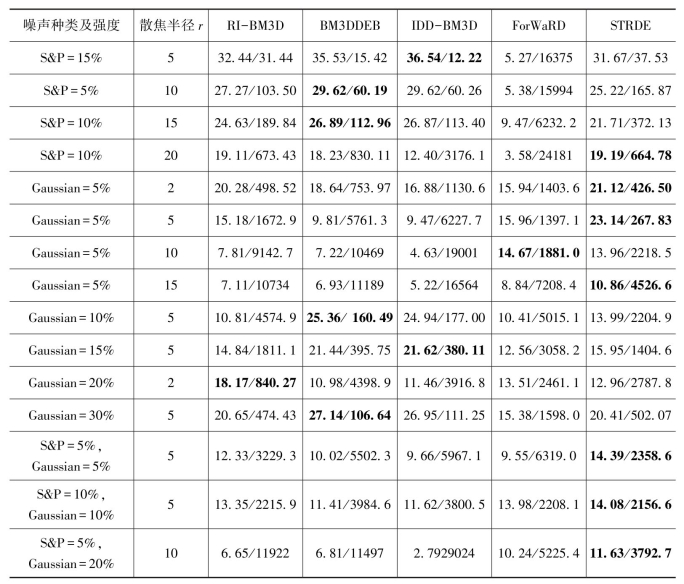
注 S&P为脉冲噪声,Gaussian指高斯噪声。
表7-3 灰度图像Mandrill受不同程度散焦模糊和不同噪声影响降质再由不同算法将其复原后的PSNR(dB)和MSENS
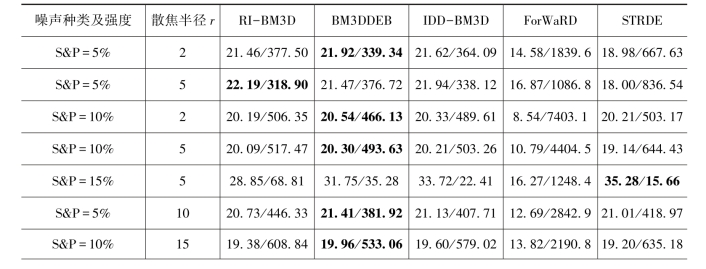
续表
注 S&P为脉冲噪声,Gaussian指高斯噪声。(https://www.daowen.com)
表7-4 彩色图像Airplane受不同程度散焦模糊和不同噪声影响降质再由不同算法将其复原后的PSNR(dB)和MSENS
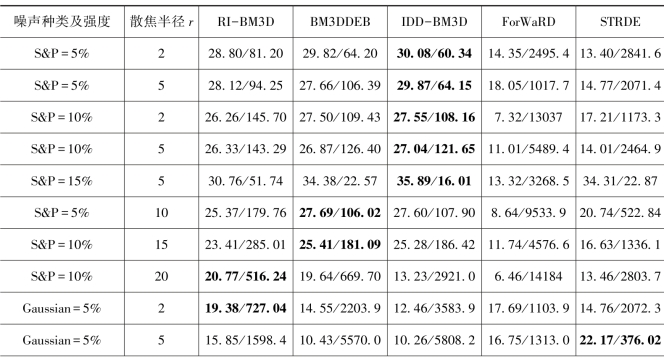
续表
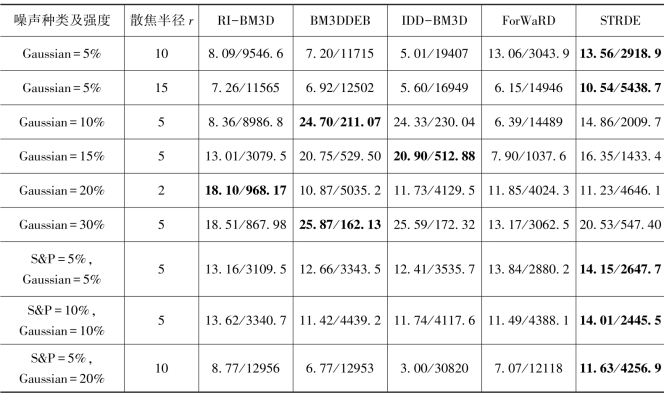
注 S&P为脉冲噪声,Gaussian指高斯噪声。
(2)图像细节信息保护的性能实验。关于降质图像复原算法对图像细节信息保护的性能分析,可参考图7-6~图7-8所示实验结果。通过本章所提出的算法STRDE与其他算法(包括RI-BM3D,BM3DDEB,IDD-BM3D及ForWaRD)的对比实验,给出图像Peppers,Mandrill与Airplane受不同程度散焦模糊影响并附加不同强度噪声干扰降质再由各类降质图像复原算法恢复后的效果图。
图7-6展示了Peppers受散焦半径为r=10的散焦模糊影响并附加20%高斯噪声干扰的降质图像和由各类复原算法将其复原后的图像(复原图像按从左至右、从上至下的顺序,依次排列为:散焦模糊图像,STRDE(PSNR=23.14),IDD-BM3D(PSNR=9.47),RI-BM3D(PSNR=15.18),BM3DDEB(PSNR=9.81),ForWaRD(PSNR=15.96),根据主观评价与客观评价获知,本章所提出的算法STRDE对于受一定程度散焦模糊影响并附加单一噪声干扰的灰度图像具有较好的图像细节信息保护能力。
图7-7展示了Mandrill受散焦半径为r=10的散焦模糊影响并附加20%椒盐噪声、5%高斯噪声干扰的降质图像和由各类复原算法将其复原后的图像(复原图像按从左至右、从上至下的顺序,依次排列为:散焦模糊图像,STRDE(PSNR=25.00),IDD-BM3D(PSNR=14.40),RI-BM3(PSNR=17.29),BM3DDEB(PSNR =15.96),ForWaRD(PSNR= 16.80),根据主观评价与客观评价获知,本章所提出的算法STRDE对于受一定程度散焦模糊影响并附加混合噪声干扰的灰度图像具有较好的图像细节信息保护能力。
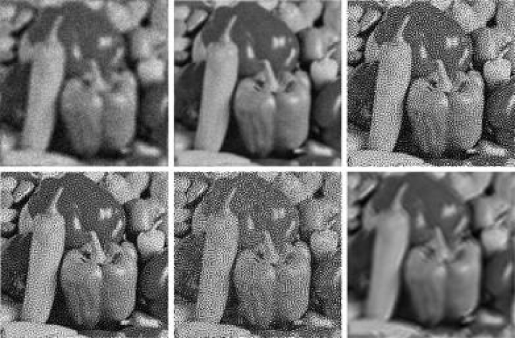
图7-6 Peppers图像受散焦模糊(半径r=10)影响并附加高斯噪声(20%)的降质图像及其应用不同算法复原后的图像
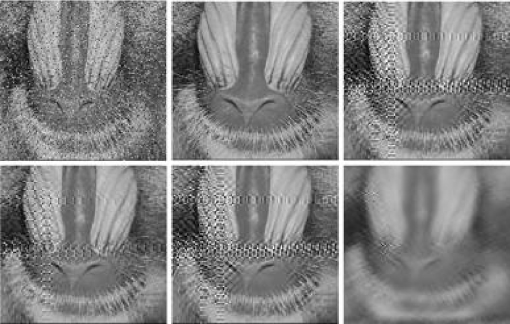
图7-7 Mandrill图像受散焦模糊(半径r=10)影响并附加椒盐噪声(20%)与高斯噪声(5%)的降质图像及其应用不同算法复原后的图像
图7-8展示了Airplane受散焦半径为r=5的散焦模糊影响并附加5%椒盐噪声、5%高斯噪声干扰的降质图像和由各类复原算法将其复原后的图像(复原图像按从左至右、从上至下的顺序,依次排列为:散焦模糊图像,STRDE(PSNR=14.39),IDD-BM3D(PSNR=9.66),RI-BM3D(PSNR=12.33),BM3DD-EB(PSNR=10.02),ForWaRD(PSNR=9.55),根据主观评价与客观评价获知,本章所提出的算法STRDE对于受一定程度散焦模糊影响并附加混合噪声干扰的彩色图像具有较好的图像细节信息保护能力。

图7-8 Airplane图像受散焦模糊(半径r=5)影响并附加椒盐噪声(5%)与高斯噪声(5%)的降质图像图像及其应用不同算法复原后的图像
由上述实验结果获知,本章所提出的算法STRDE对比其他算法可在复原后的图像中保留更多的细节信息,特别在散焦模糊降质图像的复原过程中,其去除模糊的性能表现较好,且对于不同噪声干扰也具有一定的鲁棒性。
3.算法效率分析
仿真实验在1.86 GHz CPU与1GB RAM配置的PC上运行,本章所提出的算法STRDE与ForWaRD,RI-BM3D,BM3DDEB及IDD-BM3D算法针对同一降质图像、在相同运行条件下分别完成50次图像复原实验并测算其平均运行时间,实验运行数据如图7-9所示。实验运行结果表明,与其他算法相比,本章所提出的降质图像复原算法STRDE平均运行时间仅略有增加,但其图像复原能力与图像细节信息保护能力远优于其他算法。因此,综合评价各类降质图像复原算法的成效与代价,本章所提出的基于结构张量—反应扩散理论的散焦模糊降质图像复原算法STRDE具有较好的性能。
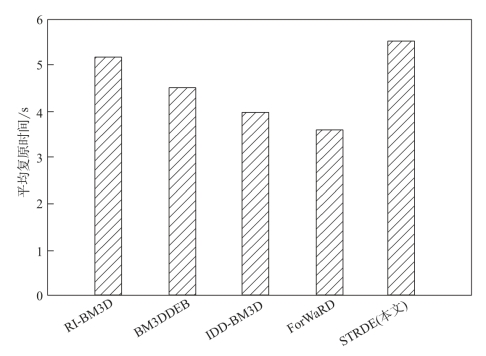
图7-9 各类降质图像复原算法的运算效率
