降质图像复原模型

一、降质图像复原模型

基于扩散过程的PM模型能够有效地复原降质图像的质量,但其在保护复原后图像的细节信息方面表现并不理想。为了进一步恢复并增强复原图像的细节信息,本章提出基于反应扩散方程的降质图像复原模型(reaction-diffusion　equation　basedimage　restoration,简称RDER),该模型不仅可用于去除图像的运动模糊,而且对于捕获图像时引入的噪声干扰(包括脉冲噪声、高斯噪声及其混合噪声)具有一定的鲁棒性。本章所提出的RDER模型可描述为:

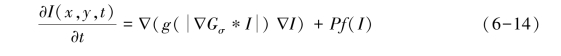
式中:P为常数,P=1/|∇I|,能够自适应地增强图像的细节信息(如边缘、纹理等);Gσ表示高斯平滑核函数,即

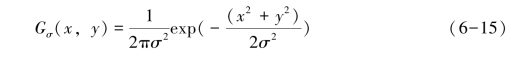
式中:σ为平滑尺度因子;x与y表示图像中像素点的位置;扩散函数g(|x|)满足公条件: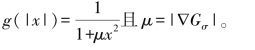

在上式中,反应项f(I)描述一个量化过程。为提高算法效率,可由参数P来控制且该参数能够自适应地调节。所以Pf(I)可描述如下情况:当梯度较大时,图像中包含较多边缘、细节信息,量化过程较慢;当梯度较小时,图像中平滑部分较多,量化过程较快。

因为图像的灰度值在一定数值范围内的特征属于高斯分布,所以我们采用Lloyd最大化方法来设计图像量化器Qs[63]。本章使用f(x)描述量化器Qs:

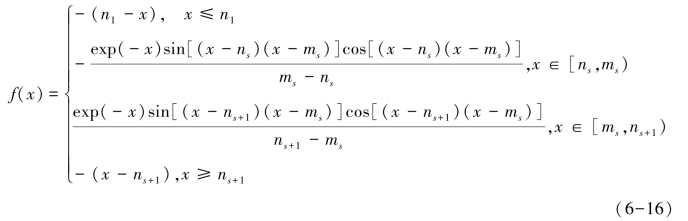
式中:s为量化器Qs的量化级数,本章中量化级数取值为s=3;量化器Qs的代码字和分离项满足:n1＜m1＜n2＜m2＜…＜ns＜ms＜ns+1。

由于仿真实验的运算需求,将连续RDER模型离散化,可将其可扩展为:

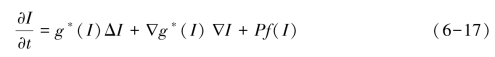
式中:。

由其差分格式推导,离散RDER模型描述如下:

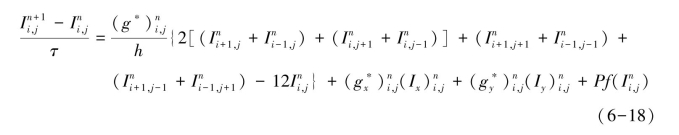
式中:τ和h分别表示时间步长因子和空间步长因子(τ和h的取值将在实验分析部分给出);截断误差为O(τ+h2),且该差分格式满足L∞稳定性(其稳定性证明将在下一小节模型分析部分给出)。

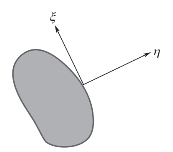
图6-3　图像的法向量和切向量

1.RDER模型对于降质图像的复原能力

令η表示图像中的法线单位向量,ξ表示图像中的切线单位向量,图6-3为图像的法向量和切向量示意图[64-65]。其中图像I的梯度可由下式表示:

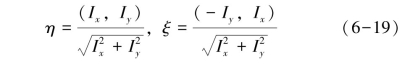
关于I(x,y)的二阶导数为:

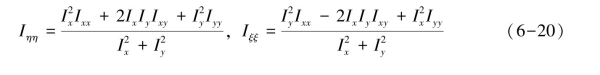
扩散过程如下:

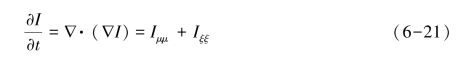
若分别只按照切向和法向扩散,则:

如果图像中像素点满足:

则表明该像素点在图像边缘上(即为图像的边缘),则:

其扩散项可用下式来表示:

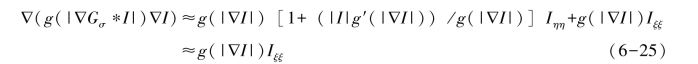
如果像素点被模糊或者受到噪声干扰,则:

其扩散项可由下式表示:

由此可见,扩散项可同向异性扩散。因此,RDER模型能够复原图像的质量同时还保护图像的边缘与细节信息,证明其对于降质图像具有复原能力。

2.RDER模型的解的存在性

为了证明RDER模型的解的存在性、稳定性和唯一性,我们考虑在图像中进行周期延拓(即令函数I∈C([0,T]×R2),且T＞0),此时求RDER模型的黏性解。

为了简化证明过程,公式(6-14)中常参数σ,μ与P取值为σ=μ=P=1,则考虑如下柯西式[57]:

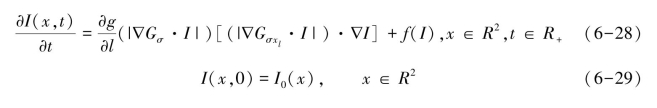
其中,

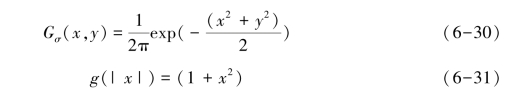
设I(x,t)与v(x,t)为RDER模型的两个黏性解,此时对于所有满足φ∈C2(R2×R)且在任意点(x0,t0)∈R2×(0,T],I-φ具有最大值,即:

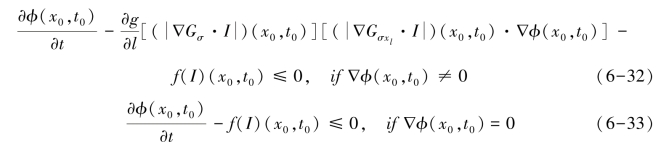
定理1:令I0(x)∈W1,∞(R2)∩C(R2),对任意的T∈[0,　+∞],RDER模型有唯一的黏性解I(x,t)∈L∞(0,T,W1,∞(R2))∩C([0,T]×R2),且对于任意的x∈R2,满足:此外,如果v(x,t)是初值为v0的RDER模型的黏性解,且v0(x)∈W1,∞(R2)∩C(R2),则对于任意的T∈[0,+∞],有:

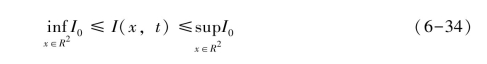
证明:如果I(x,t)是公式(6-28)在R2×R+上的黏性解,则:

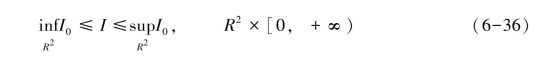
令式(6-32)中φ=sup R2I+δt(δ＞0),设(I-φ)在点(x0,t0)且T＞0处取得最大值,则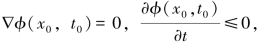这与在R2×(0,+∞]上矛盾。因此,I(x,t)-φ(x,t)在t0=0时取得最大值,即:

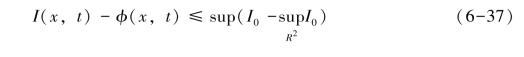
则:

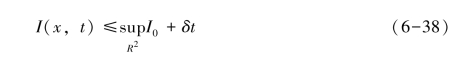
同理,有:

令δ→0,即可得下式:

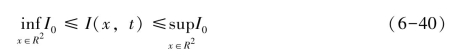
下面给出梯度估计的近似解,考虑下面的柯西式:

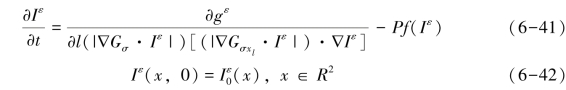
其中0＜ε＜1,gε(s)=g(s)+ε,Iε∈C∞(R2),对于Iε→I有:

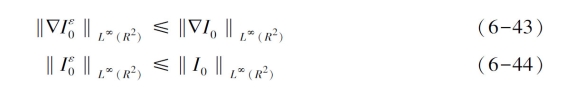
根据拟线性抛物方程的特征,公式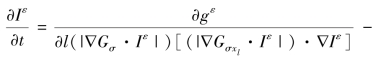具有光滑解Iε∈C∞([0,∞)×R2),　且对于xk求微分,并于公式两边均乘以2Iεx,则有:

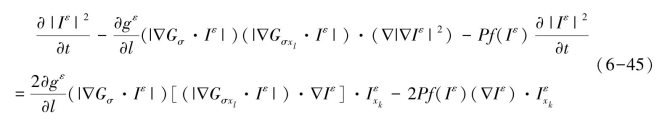
由gε和Gσ的定义可知:

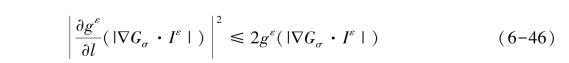
对于任意α,当|α|＜2时,有:

式中:　C是常数,且C＞0,根据柯西不等式,有:

C仅与初始条件I0有关,利用Cauchy-Schwarz不等式和最大值原理,得:

式中:Ct为非负常数,CT仅与T、初始条件I0有关,因此,对于任意(x,y)∈R2和t∈[0,T],有:

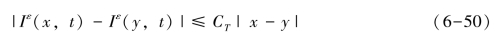
和

根据Ascoli-Arzela定理,存在函数:其中ε→0,Iε一致收敛于I(x,t)。

下面证明I(x,t)是公式g(|x|)=(1+x2)的黏性解。令Φ∈C2(R2×R),设I-Φ在(x0,y0)∈R2×R+有局部最大值,且Iεk→I,Iεk-Φ在点(xk,yk)处有局部最大值,因此,当k→∞时有(x0,y0)→(xk,yk),在点(xk,yk)处有∇Iεk=∇Φ,,　则:

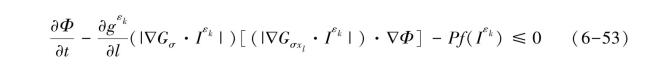
如果∇Φ(x0,t0)≠0,　上式变形为:

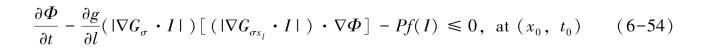
如果∇Φ(x0,t0)=0,　则上式变形为:

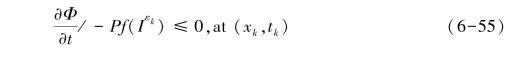
由于∇Φ(xk,tk)→0,εk→0,k→∞,　因此Iε一致收敛于I(x,t);因为I(x,t)是公式g(|x|)=(1+x2)的黏性解,所以RDER模型存在解。

至此,RDER模型的解的存在性证毕。

3.RDER模型的解的稳定性

定理2:令M1,M2满足M1＜n1＜nq+1＜M2,且sτ＞0,sh＞0,对于τ≤sτ,h≤sh,如果M1＜‖In‖∞＜M2,则下式成立。

证明:令τ/h=ε,本章中使用Ψu,v(其中-1≤u,v≤1,且u2+v2≠0)表示公式=∇·(∇I)=Iμμ+Iξξ的系数,则公式=∇·(∇I)=Iμμ+Iξξ可变形为:

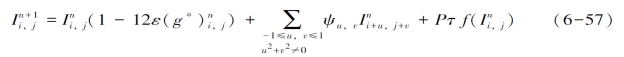
式中:

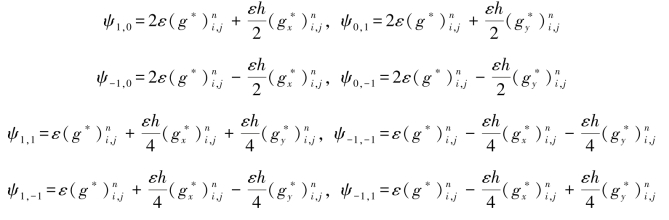
由于g(0)=1且,因此当g≤1,则:

假设下列不等式成立：

令M*=max{-M1,M2}且M*=max{-M2,M1},则有:

(1)若。由f(x)定义可推导得:

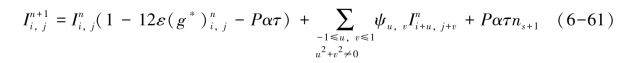
如果满足下述条件:

如果满足下述条件:

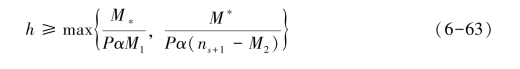
则有。

(2)若。假设函数f(x)　在[n1,ns+1]　区间的上界分别为β和γ,则:

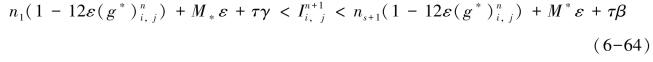
有:

(如果满足下述条件:则有。

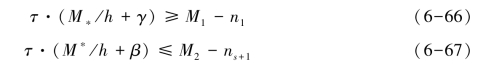
(3)若。推导过程同(a)所示,如果满足下述条件:则有。

由上述条件公式推导得:

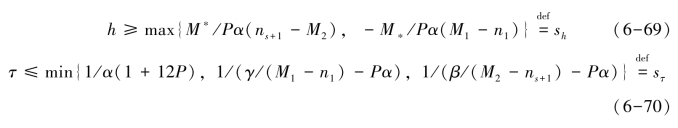
所以公式满足L∞稳定性。

至此,RDER模型的解的稳定性证毕。

4.RDER模型的解的唯一性

证明:根据前面的定理1,设x,y∈R2,t∈[0,T],ε＞0,λ＞0,σ＞0,I0和v0是黏性解I(x,y)和v(x,y)的初始条件,令:

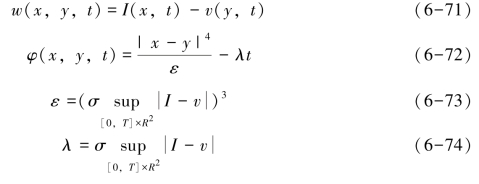
假设w-φ在点(x0,y0,t0)处取得局部最大值,在t0=0处w-φ有最大值,则:

即

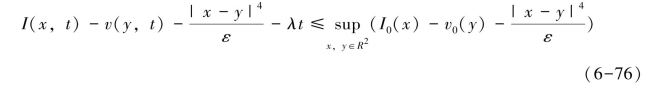
特别地,上式中当x=y时,有:

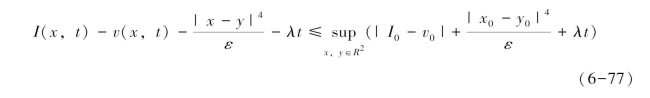
合并上述公式,得:

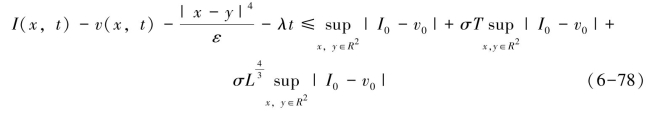
在R2×[0,T]中,将以上各式中I与v互换,即w(x,y,t)=v(x,t)-I(y,t),则可导出:

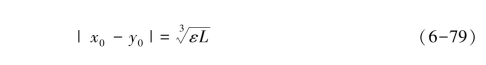
式中:L是Lipschitz常数　。

令σ=0,则有:

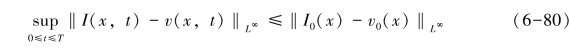
令I0=v0,则可推导得公式。

至此,RDER模型的解的唯一性证毕。

总结并归纳RDER模型的性质,根据本章节关于运动模糊降质图像复原模型的描述,建立基于RDER的降质图像去除运动模糊的数学模型,则离散RDER模型中(Ix)i,j与(Iy)i,j的定义如下: