一、结构张量
图像中包含有大量结构信息如边缘、纹理等,这些信息已在图像识别、目标检测、计算机视觉等研究领域获得广泛应用。结构张量(structuretensor,简称ST)作为一种重要的图像分析与处理工具,常被用于图像中结构信息的方向场、边缘、角点及其他图像几何特征的检测[73-74]。因此,结构张量ST可与其他理论共同解决图像处理领域不断出现的新问题,具有重要的研究价值。ST定义[75]如下:
假设Ω⊂R2为任一灰度图像的像素值矩阵,则该灰度图像可表示为g:Ω→R;若图像g中任一像素点的梯度为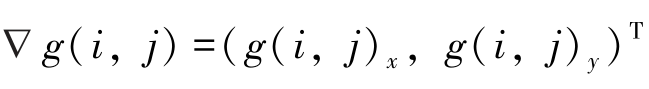 , 则任一像素点的ST为:
, 则任一像素点的ST为:
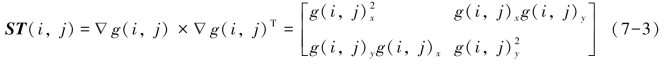
由式(7-3)可知,图像g中任一像素点的ST为一个2×2的对称矩阵,而图像的ST即为其梯度的张量积。
在实际问题的研究中,可通过ST求解图像的方向场、边缘、角点等几何结构信息。式(7-3)中所示的ST可由图像梯度表示,因为图像梯度对噪声干扰非常敏感,所以ST易受影响。为提高ST对于噪声的鲁棒性可采用平滑处理的方法,即用高斯核函数与式(7-3)中的ST作卷积,获得线性结构张量(linear structure tensor,简称LST):
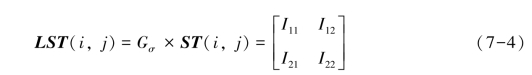
式中:Gσ为方差σ的高斯核函数,且σ的取值与平滑程度有关。
因为上式所示的LST能够有效抑制噪声并同时展现图像的方向场、边缘、角点等几何结构信息,所以LST的应用范围变得更加广泛。求解上述公式,得LST的两个特征值λ1和λ2:
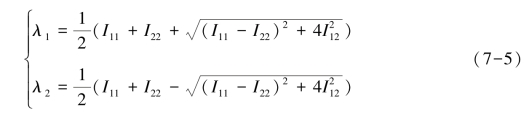
其相应的特征向量为:
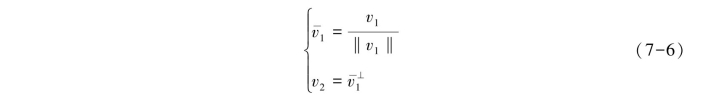
式中:![]() (https://www.daowen.com)
(https://www.daowen.com)
LST的特征值λ1和λ2主要用来描述图像中结构信息的强度,例如,LST的最大特征值体现了图像的最大对比度;LST的特征向量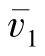 和v2主要用来描述图像中结构信息的方向,如图7-3所示,其中
和v2主要用来描述图像中结构信息的方向,如图7-3所示,其中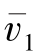 表示图像中局部对比度最大的方向信息(即法线方向),v2表示图像中局部对比度最小的方向信息(即切线方向)。
表示图像中局部对比度最大的方向信息(即法线方向),v2表示图像中局部对比度最小的方向信息(即切线方向)。
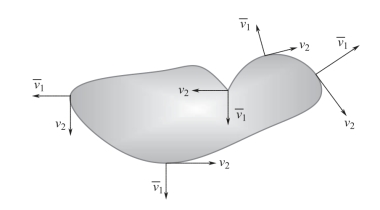
图7-3 图像结构的方向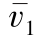 及其正交方向v2的示意图
及其正交方向v2的示意图
LST的特征值满足不同条件时可展现图像中不同特征的结构信息:
①图像的平滑部分。在该区域中的图像像素点的灰度值变化较小,因此所对应LST的特征值λ1,λ2满足λ1≈λ2≈0;
②图像的边缘部分。在该区域中的图像像素点的灰度值沿某一方向变化较大,因此所对应LST的特征值λ1,λ2满足λ1>λ2≈0;
③图像的角形部分或“T”形部分。在该区域中的图像像素点的灰度值在两个正交的方向上变化均较大,因此所对应LST的特征值λ1,λ2满足λ1≥λ2>0。
因为结构张量能够较好地描述图像的几何结构特征,所以近20年来结构张量一直被广泛应用于图像处理领域的各研究方向:
①结构张量应用于检测工程。因为结构张量的特征值能有效地描述图像中的角点部分,所以基于结构张量的角点检测器广泛用于检测工程;此外,为进一步提高检测精度,还可结合滤波方法用以增加检测器的鲁棒性,改进应用结构张量的检测方法;
②结构张量应用于图像分割。因为基于结构张量的图像纹理特征能够被准确、有效地提取,所以应用这些纹理特征分割图像可取得较好的效果;
③结构张量的其他图像应用。如图像模式分类、图像分析等。
