运动模糊的数学模型
通过研究成像目标在匀速直线运动中的图像投射过程,分析并构建运动模糊图像降质模型[58-59]。因为客观世界中变速或非直线运动在一定时空条件下均可分解为分段的匀速直线运动,所以与匀速直线运动关联的运动模糊图像降质模型具有普遍适用性,且是构造其他复杂运动模糊图像降质模型的基础。
假设成像固件完好、无噪声干扰、外界大气透光与折射率正常、拍摄聚焦正常,引入时间参数t标记成像目标、图像的运动属性。s(x,y,t)记录某时刻成像目标,g(x,y,t)记录捕获图像与曝光时间的关系,并可以表示为成像目标在特定时间段内的积分[58],则:
![]()
若成像目标静止,则s(x,y,t)=I(x,y);若成像目标运动,则s(x,y,t)=I[x-x0(t),y-y0(t)],其中x0(t)与y0(t)分别表示像素点位置因运动变化在图像平面的x与y方向上的偏移分量。最终捕获图像g(x,y)可以表示为成像目标s(x,y,t)在图像曝光时间T内连续成像的迭加(即匀速直线运动关联的图像运动模糊的连续数学模型[58]),将s(x,y,t)在运动情况下的表达式代入上式, 得:
![]()
由该模型推断捕获图像g(x,y)的模糊程度受图像像素点偏移量影响,并随运动时间t增加而增大。若以成像平面的水平方向为x轴(图6-1),成像目标在x方向上做匀速直线运动,上式可简化得:
![]()
若图像总位移量K与运动总时间(即曝光时间)T可通过测量获得,则运动在x方向上的位移分量可表示为x0(t)=Kt/T,将其代入上式得:(https://www.daowen.com)
![]()
结合模糊图像在成像过程中的离散性与迭加性(即运动模糊图像各点像素值为原图像各点像素值与其对应成像时间乘积的累加),上式的离散化形式可表示为:式中:L表示运动目标投射图像移动的像素个数(注:整数值近似表示);Δt表示各像素点对于图像模糊效果的时间影响因子。
![]()
实际成像过程中,成像设备每次曝光时间、成像目标运动速度等参数难以测定;根据图像模糊的物理意义(即运动模糊图像可以视为同一拍摄场景经若干次位置偏移的迭加[59],图6-2),将影响图像模糊的时间因素转化为距离因素,便于应用并可简化上式得:
![]()
假设在信号量处理时忽略噪声干扰,图像降质模型的一般形式可简化为模糊图像降质模型,如下式所示;以卷积形式重新表述上述公式,在匀速直线运动过程中运动模糊图像降质模型可表示为:
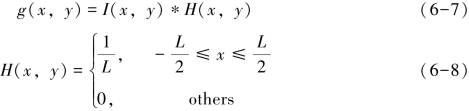
式中:系统函数H(x,y)常被称为模糊算子或点扩散函数(point spread function,PSF)。若成像目标运动方向与成像平面存在夹角θ,则运动模糊图像降质模型的模糊算子H(x,y)可表示为:
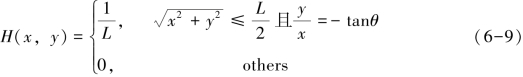

图6-2 Lena图像受不同程度运动模糊影响并附加各类噪声干扰的降质图像及其对应的频谱图像
