1.2.2 膜计算模型介绍
下面就本书涉及的两类膜系统(类细胞膜系统和类组织膜系统)做简单介绍。
1.2.2.1 类细胞膜系统
类细胞膜系统主要包括转移P系统、转运P系统和活性膜P系统等。转移P系统的主要特点是在各个膜内单独使用多重集重写规则模拟生化反应。文献[21]首次提出了转运P系统,其中物质可以在各个膜之间进出完成计算,但是这些物质并不发生改变。这类系统中的规则主要有两类:共运输和逆运输。这两种规则的差异主要体现在两个对象在穿过细胞膜时方向不同。活性膜P系统是一类极其重要的类细胞膜系统,其规则包括膜溶解、膜分裂、膜创建等。
在类细胞膜系统中,细胞膜按嵌套分层的方式划分为若干个区域,每个区域称为一个膜,膜中对象通过相应的规则实现计算。皮肤膜外部区域称为环境。一个膜结构中膜的数目表示该膜结构的度。图1-1(a)展示了生物细胞膜的真实结构,图1-1(b)展示了抽象形成的类细胞膜系统的膜结构。对于该膜结构,最外层膜称为皮肤膜,膜标签为2、3、5、7、8、9的膜为基本膜(分别简称为膜2、膜3、膜5、膜7、膜8、膜9)。在一个类细胞膜系统中,对象的多重集被放置在由膜结构所限定的区域内。对象可以进化,并可穿过相邻的细胞膜。简单地说,该结构采用分层排列并用膜标签来标识这些膜,每个膜内可以包含对象的多重集。由此,所获得的计算装置是一个分布式并行系统,对象的多重集(化学物质)放置在区域(树结点)以及通过一些规则(生化反应)进行处理。可以把P系统看作是一个计算机器,从初始状态(用对象的多重集和膜结构表示)开始,通过应用膜结构中的进化规则编码的程序完成计算。
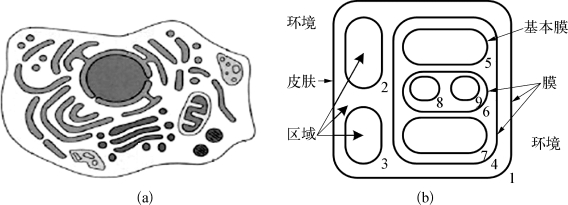
图1-1 类细胞膜系统的膜结构[22]
(a)细胞膜;(b)膜结构
除了图1-1(b)所示的膜结构外,膜结构还可以用广义表和树形结构表示:广义表是用“[]”来表示一个膜,“[]”的下标表示膜的序号,如基本膜i用[]i表示,膜j中嵌套膜i可表示为[[]i]j。图1-1(b)用广义表表示为[[]2[]3[[]5[[]8[]9]6[]7]4]1。图1-1(b)也可以用树形结构表示,如图1-2所示。
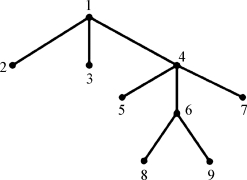
图1-2 膜结构的树形结构
受不同生物特性和生物实际的启发,许多类细胞原始模型的变体先后被提出。下面仅介绍两类与本书有关的模型:活性膜P系统模型和膜上带蛋白的P系统模型。
1)基于活性膜的P系统模型
作为类细胞膜系统中一类重要模型,基于活性膜的P系统由G.Pǎun院士于2001首次提出[23]。该膜系统中每个细胞膜上都带有电荷,即“+”(正电荷)、“-”(负电荷)和“0”(中性)。通过使用规则,这些膜上的电荷属性可以发生改变,比如从中性变为正电荷等。当然,膜上的电荷也可以保持不变。另外,这类膜系统的一个重要特点是,通过使用一些规则(如分裂规则、溶解规则等),膜结构可随着计算发生改变。基于活性膜P系统中的膜结构可以用广义表来表示,例如![]() 。
。
定义1.1:一个度为m(m≥1)的活性膜P系统可定义为
Π=(O,H,μ,w1,…,wm,R,iout),
其中,O是对象字母表;H是膜标签的有限集合;μ表示膜结构,包含m个膜,每个膜的标签号是集合H中的元素;w1,…,wm表示O上的字符串,用来表示各个膜内初始状态的对象多重集;iout是输出区域,用来保存最后的计算结果;R为规则的有限集合,这些规则包含下面几种类型。
(1)对象进化规则:![]()
如果对象a出现在膜标签为h的膜中,则该规则可以应用于当前格局中。通过应用此规则,对象a进化为多重集b。
(2)通信规则1![]()
对象a进入膜中并且在该过程中这个对象可以发生改变。同时,膜上电荷也可以改变,但是膜标签保持不变。
(3)通信规则2:![]()
对象a被发送到膜外并且可以发生改变。同时,膜上电荷可以改变,但是膜标签保持不变。
(4)溶解规则:![]()
在膜中对象a的影响下,膜可以溶解。溶解的同时,该膜中的对象a可以发生改变。
(5)基本膜分裂规则:![]() 0},a、b、c∈O。
0},a、b、c∈O。
在膜中对象a的影响下,该规则将原始膜分裂为两个具有与之相同膜标签的新膜。在产生的两个新膜中,分别产生对象b和c。膜h内剩余物质分别复制到这两个新膜中。
(6)规则(5)的扩展规则:其形式如下。
非基本膜分裂规则:![]() {+,-,0},a、b、c∈O。
{+,-,0},a、b、c∈O。
与规则类型(5)不同的是,分裂产生的新膜与初始膜可以具有不同的膜标签号。
系统初始格局为(w1,…,wm,μ),即由放置在相应膜中的多重集w1,…,wm来表示。在膜系统的工作过程中,由每个膜中相应的对象多重集以及膜结构来描述当前格局。
膜计算理论研究受到各种生物实际启发的模型计算能力以及计算效率。对于计算能力,一般是研究系统的计算通用性。已经证明,活性膜P系统是计算通用的[23]。此外有文献也对活性膜P系统中规则的类型、膜的数目等方面的变化对系统通用性的影响进行了研究[24]。
通过使用活性膜P系统中的膜分裂规则创建新膜,可以在线性时间内产生指数级的计算空间。利用空间换时间,使得在有效时间内求解NP难问题成为可能。因此,活性膜P系统可以用于求解NP难问题,例如SAT问题[25]、子集和问题[26]等。但这些研究仅针对标准膜系统,即系统中每条规则的执行时间为一个单位时间。然而,由于很多不可控制的因素,不同生化反应所需时间是无法控制的,从而难以建立鲁棒性较好的膜系统。
2)基于膜上带蛋白膜的P系统模型
对于实际动物细胞的细胞膜,其组成物质中一半以上为生物蛋白。此外,还包括如水分子以及少量碳水化合物等其他的成分[27]。膜上蛋白质可分为两类,分别为膜间蛋白和膜内蛋白。它们之间的差异在于膜间蛋白既可以作用于膜内的物质,也可以作用于膜外的物质,而膜内蛋白只能够作用于膜内的物质。膜具有双层结构,外层膜称为膜上,内层膜称为膜内。蛋白质位于膜上区域,其他物质位于内层膜中。因此,生化反应的发生主要受到膜上蛋白质的作用而完成。
A.Pǎun与B.Pǎun于2006年提出了类细胞膜系统的一种变体,即为膜上带蛋白膜系统[28]。在该系统中,细胞膜上和膜内分别含有蛋白质和物质,这与生物体中的实际情况相一致。与以往类细胞系统不同的是,这类系统中规则是在膜上蛋白质的控制下完成的。膜上的蛋白质在计算过程中一直保留在该细胞上,不会离开该细胞膜。因此,在引入蛋白质控制生化反应的机理后,膜内对象的进化不再仅依赖膜内对象,还需要考虑膜上蛋白质的控制因素。
在膜上带蛋白膜系统中,如果蛋白质p在一个膜标签为h的细胞膜上,记为[p|]h。例如,对于一个细胞膜h,在该细胞膜上有蛋白质多重集pq,细胞膜内含对象多重集abc 2,可以记为[pq|abc 2]h。(https://www.daowen.com)
定义1.2:使用膜分裂的膜上带蛋白膜系统表示为
Π=(O,P,μ,w1/z1,…,wm/zm,E,R1,…,Rm,iout)
其中,O表示对象的字母表;P表示膜上蛋白质的字母表(O∩P=Ø);μ表示初始膜结构,分别用1,…,m进行标记;wi(1≤i≤m)表示在初始膜结构中相应膜i中的对象多重集;zi(1≤i≤m)表示在初始膜结构中相应膜i上蛋白质的多重集;E⊆O表示环境中的对象;iout表示输出区域,该区域保存最后的计算结果;R1,…,Rm表示区域1,…,m中规则的有限集,这些规则包含下面几种类型。
(1)进化规则1:
[p|a]h→[p|b]h,[p|a]h→[p′|b]h,p、p′∈P,a、b∈O,1≤h≤m。
当某个对象a出现在膜h中时,受到膜h上蛋白质p的影响,该对象进化为另一个对象b。在此过程中蛋白质可能发生改变,也可能保持不变。
(2)进化规则2:
a[p|]h→b[p|]h,a[p|]h→b[p′|]h,p、p′∈P,a、b∈O,1≤h≤m。当某个对象a出现在膜h外时,受到膜h上蛋白质p的影响,该对象进化为另一个对象b。在此过程中蛋白质可能发生改变,也可能保持不变。
(3)进化规则3:
[p|a]h→b[p|]h,[p|a]h→b[p′|]h,p、p′∈P,a、b∈O,1≤h≤m。
当某个对象a出现在膜h内时,受到膜h上蛋白质p的影响,该对象被发送到膜h外。在此过程中蛋白质和该对象可能发生改变,也可能保持不变。
(4)进化规则4:
a[p|]h→[p|b]h,a[p|]h→[p′|b]h,p、p′∈P,a、b∈O,1≤h≤m。
当某个对象a出现在膜h外时,受到膜h上蛋白质p的影响,该对象被发送到膜h内。在此过程中蛋白质和该对象可能发生改变,也可能保持不变。
(5)进化规则5:
a[p|b]h→c[p|d]h,a[p|b]h→c[p′|d]h,p、p′∈P,a、b、c、d∈O,1≤h≤m。
当某个对象a出现在膜h外时,对象b出现在膜h中,受到膜h上蛋白质p的影响,膜外对象被送到膜h内,同时膜内对象被送到膜外。在此过程中蛋白质和发生移动的所有对象均可能发生改变,也可能保持不变。
(6)分裂规则:
[p|]h→[p′|]h[p″|]h,p、p′、p″∈P,1≤h≤m。
该原始膜不能为皮肤膜。膜h可以为基本膜,也可以为非基本膜,受到膜h上蛋白质p的影响分裂为两个具有相同标签的膜。在此过程中原始膜上的蛋白质可能发生改变,同时,膜内的其他物质都将被复制到新产生的两个膜内。
初始格局为(w1/z1,…,wm/zm,μ),即通过放置在相应膜中的对象多重集w1,…,wm,以及放置在相应膜上的蛋白质多重集z1,…,zm来表示。系统通过使用以上规则,可以得到连续而有限的格局。这些格局之间的转移称为计算。在系统的每个计算步中,当前格局由系统中膜内对象多重集、膜上蛋白质集合以及膜结构共同组成。规则的长度为以上进化规则中膜上蛋白质以及膜内对象的总数。
在文献[28]中,膜上带蛋白膜系统在仅仅使用一个膜的情况下就能构建一个通用的计算膜系统。同样,引入分裂规则后,该系统也可以在多项式时间(甚至线性时间)内求解NP完全(NP-C)问题。但是这类膜系统中膜上每种蛋白质的可达状态并没有做任何限定。随后提出的触发型膜上带蛋白膜系统中每种蛋白质只有两种可达状态。当这类膜系统的概念被提出以后,其通用性也有文献进行了研究报道[29]。
尽管膜上带蛋白膜系统模型已经提出了多年,但是国际上对于该模型的研究不多,而在涉及时间无关模式下的研究更少。另外,触发型膜上带蛋白膜系统在时间无关模式下计算效率的研究还尚未开展。
1.2.2.2 类组织膜系统
细胞是构成生物体的基石。从生物学角度来看,细胞在生物体中并不独立存在,而是不断地与其他细胞以及环境中的物质进行交互作用。细胞与细胞之间或者细胞与环境之间可能存在蛋白质通道,这些蛋白质通道使得大量细胞之间相互交流就构成了复杂的通信网络。受到这些生物体中活细胞结构和功能的启发,文献[9]在2002年首次提出了类组织膜系统。
类组织膜系统是类细胞膜系统的一种重要拓展。与类细胞膜系统中膜结构可以用树形结构表示不同,对于类组织膜系统,其细胞结构可以用图来表示,即把分布在环境中的每一个细胞看成一个图中的顶点,而各个细胞之间的交流通道看成图中的边。细胞之间以及细胞与环境之间都能进行物质交流。类组织膜系统中的细胞不带电荷,而且规则相对简单,因此易于实现。如果系统中各细胞之间的通信通道是事先固定的,则称之为基本组织型膜系统;相反如果通信通道是在计算过程中动态创建的,则称之为种群P系统[30]。本书研究的类组织膜系统都是基于基本组织型膜系统的。
定义1.3:一个度为m(m≥1),使用细胞分裂的类组织膜系统可表示如下:
Π=(O,E,w1,…,wm,R,iout),
其中,O为对象的字母表;E⊆O表示初始状态下环境中存在的任意多份对象的集合;wi(1≤i≤m)表示在初始状态下各个区域中在字母表O上的对象多重集;iout表示输出区域,该区域保存最后的计算结果;R表示规则集合,这些规则包含下面两种类型。
(1)通信规则:(i,u/v,j),其中i、j∈{0,1,…,m},i≠j,u、v∈O*,|uv|>0,i和j分别对应细胞i和细胞j;如果i=0或者j=0,则对应的是环境。当多重集u出现在细胞i中,而且多重集v出现在细胞j中时,多重集u从细胞i发送到细胞j中,同时多重集v从细胞j发送到细胞i中。在类组织膜系统中,规则的长度定义为|u|+|v|。
(2)分裂规则:[a]i→[b]i[c]i,其中i∈{1,…,m},a、b、c∈O,i≠iout。该分裂规则执行时,原始细胞分裂为两个具有相同标签的细胞。在这两个新产生的细胞中,对象a被分别替换成对象b和c,同时原始细胞中的其他物质分别复制到新产生的细胞中。分裂规则可以在线性时间内生成指数级的工作空间,因此,从理论上讲,许多NP难问题可以在多项式时间甚至线性时间内得到解决。
任何时刻系统的格局由所有细胞中的物质以及环境中的对象多重集来描述。与类细胞膜系统不同的是,类组织膜系统中只要任意两个细胞之间存在通信通道,这两个细胞就可以直接进行物质交流。而且,细胞之间也可以通过环境间接进行物质交流。对于类组织膜系统,环境中可以存在对象的任意多份物质,并且可以进入任何一个细胞中。因此环境中的物质可以为系统的运行提供巨大的能量。
在类组织膜系统中主要有两种方式来产生新的细胞,包括细胞分裂和细胞分割。在本书的研究中仅涉及细胞分裂,即产生的两个细胞中除一对不同的对象外其他物质完全相同。2008年,文献[31]首次把细胞分裂引入类组织膜系统中并在多项式时间内求解了SAT问题。随后,带细胞分裂的类组织膜系统也解决了其他NP难问题,例如顶点覆盖问题、子集和问题等。
对于以上介绍的类细胞膜系统和类组织膜系统,下面简要介绍它们的工作方式。其中的规则根据以下原则应用:①非确定性。将对象非确定地分配给可以应用的规则。例如,假设系统在运行的某个时刻,有n条规则可以应用于某个对象,但仅有m(m<n)个对象,那么这m个规则中选择哪些规则执行是不确定的。②极大并行性。系统在运行的某个时刻,所有可以被应用的规则都必须同时并行应用。
值得注意的是,如果某个对象可以同时应用到多个规则中,那么系统只能非确定地随机选取其中一条规则执行。只有当这条规则执行结束后,该对象才能参与到其他规则的应用中。在多个膜(细胞)内以极大并行的方式应用规则,所有可以被应用的规则都必须同时被并行应用。系统根据各自的模型选择对应的规则,这样就可得到系统格局之间的转移。系统开始运行后,当前格局由上一个格局通过极大并行应用规则而获得。最后,假若没有规则可以应用于当前格局,而且没有规则正在执行之中,则计算停止。
之前研究的膜系统称为标准膜系统,即假设存在一个全局时钟,系统中每条规则的执行时间为一个单位时间,即系统中每条规则的执行时间都是相同的。但从生物实际来看,这个假设是比较理想化的。生化反应通常会受到多种因素的影响,导致它们的执行时间往往难以预知。因此,在生物实现方面显得相对困难。基于该生物背景,本书研究几类膜系统在时间无关模式下的计算性能。这类计算系统不受外界环境等任何因素的影响,具有较好的自适应性和鲁棒性等优点。
