1.3.2 时间无关模式
生物实际对应膜系统有三个重要的组成要素：膜结构、对象多重集以及进化规则。作为最核心的要素进化规则，标准膜系统中都假定其中每条规则的执行时间为一个单位时间。也就是说，假定每条规则的执行时间是相同的。但是，从生物实际来看，生化反应通常会受到多种因素的影响，例如温度、催化剂等。由此可见，不同生化反应所需时间往往难以预知。基于这个生物实际，很有必要考虑规则执行的时间无关性，建立能够克服规则执行时间长短的膜系统。因此，为了建立容错性能更好的计算系统，研究这些系统在时间无关模式下的计算能力以及计算效率有着重要的意义。
文献［32］提出了时间无关的概念，文献［33］将时间无关方法处理NP难问题作为公开问题。之后，文献［34］首次在时间无关模式下获得了SAT问题的半统一解。随后一些文献对各类膜系统在时间无关模式下求解NP难问题进行了研究［35-37］。但总的来说，涉及时间膜系统的研究较少，而且有的研究结果还需进一步优化，有的模型还需引入时间无关方法进行研究。于是本书去除“每条规则的执行时间为一个单位时间”这个条件，即任何规则的执行时间长短是任意的。本书主要研究几类膜系统在时间无关模式下的计算能力以及计算效率。
定义1.4：在时间无关模式下运行的膜系统简称为时间膜系统。时间膜系统中每条规则的执行时间长短是任意的，用规则启动步（rule starting step，简称RS步）［33］来刻画系统的计算效率。如果在系统的某个计算步，至少有一条规则开始执行，则这个计算步称为RS步。
时间膜系统使用时间映射e：R→N表示规则的执行时间，其中，R表示系统中的规则，N表示自然数集合中的元素。时间膜系统的工作方式如下：假定存在一个全局时钟将系统时间划分为等长的时间单元。假如在第j个时刻有一条规则r开始应用，那么该规则将会在j＋e（r）时刻停止。其中，用e（r）表示该规则的执行时间。在该规则执行期间，该规则中的物质不能被其他任何规则使用，直到在j＋e（r）＋1时刻才能应用到其他规则中。
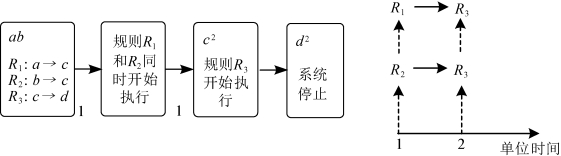
时间膜系统和标准膜系统具有完全不同的工作模式。下面用一个简单的例子来进行说明。如图1-3，膜1中有多重集ab以及规则R1、R2和R3。对于标准膜系统，系统第一个计算步同时执行规则R1和R2，生成两份对象c。然后在第二个计算步执行规则R3，两份对象c消耗并生成两份对象d。这样，经过两个单位时间以后系统计算结束。而对于时间膜系统，如图1-4，系统开始运行时同时执行规则R1和R2，但是由于时间膜系统中这两个规则的执行时间长短是不确定的，这里假设规则R1先执行结束并生成一份对象c。这时，系统执行规则R3，对象c消耗并生成一份对象d。同样，当规则R2执行结束时，系统再次执行规则R3，对象c同时消耗并生成另外一份对象d。这时，经过三个RS步后系统计算结束。
图1-3 标准膜系统中规则的执行方式
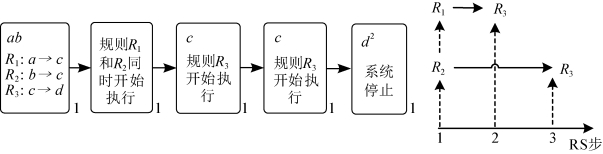
图1-4 时间膜系统中规则的执行方式
由此可以看出，时间膜系统和标准膜系统具有完全不同的运行机制。对于时间膜系统，由于规则的执行时间长短具有不确定性，通常来说时间膜系统比标准膜系统的运行过程更加复杂。而且从以上例子可以看出，时间膜系统规则执行中极大并行性可能会受到影响。在该实例中，对于规则R3的执行，在标准膜系统下是并行的，而在时间膜系统中并没有并行执行。因此，对于时间膜系统，为了使极大并行性得到最大限度的利用，解决好规则的同步问题是极其重要的。
时间膜系统的优点在于具有较强的容错性。如果系统中有规则的执行时间出现了差错，即使没有在预定时间内完成，整个系统依然可以保持正确的计算结果。一般来讲，P系统在时间无关模式下运行，会使系统的鲁棒性得到一定程度的提高。