2.5 基于促进剂的时间活性膜P系统通用性证明
下面,通过模拟注册机证明基于促进剂的时间活性膜P系统是计算通用的,即计算能力与图灵机等价或不低于图灵机。
定理2.3:![]()
证明:注册机的指令包括加法指令、减法指令以及终止指令,证明过程主要是对加法指令和减法指令进行模拟。
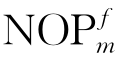 表示基于促进剂的时间活性膜P系统产生的自然数集合族,其中m表示初始膜数量,f表示时间无关。对于注册机M=(m,H,l 0,l h,I),假设其带有3个注册器,产生的数存储在注册器1中。另外,假定注册器1中没有加法指令,并且当计算结束时,除注册器1外,另外两个注册器均为空。系统构造如下:
表示基于促进剂的时间活性膜P系统产生的自然数集合族,其中m表示初始膜数量,f表示时间无关。对于注册机M=(m,H,l 0,l h,I),假设其带有3个注册器,产生的数存储在注册器1中。另外,假定注册器1中没有加法指令,并且当计算结束时,除注册器1外,另外两个注册器均为空。系统构造如下:
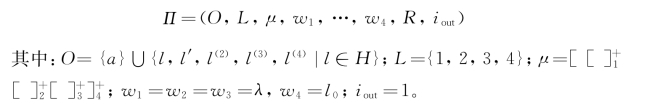
系统在时间无关模式下工作,设e是规则集合I到自然数的任意时间映射。注册机中每个注册器r对应一个膜标签为r的膜,膜r中对象a的数量就是相应注册器内的值。下面将构造规则集合R。
(1)对于每条加法指令l i:(ADD(r),l j,l k),r=1、2、3,指令集合构造如下:
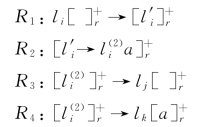 (https://www.daowen.com)
(https://www.daowen.com)
下面模拟加法指令l i。系统在某一步应用规则R 1,对象l i进入相应的膜r中,并进化为对象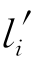 。随着对象
。随着对象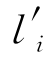 在膜r中出现,规则R 2将被应用,将会在膜r中生成一份对象a,使得对象a的数量加1,从而实现了加法指令l i的要求。同时,对象
在膜r中出现,规则R 2将被应用,将会在膜r中生成一份对象a,使得对象a的数量加1,从而实现了加法指令l i的要求。同时,对象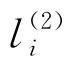 出现在膜r中。此时,系统非确定性地选择规则R 3和R 4,通过应用规则R 3(resp.,R 4),对象
出现在膜r中。此时,系统非确定性地选择规则R 3和R 4,通过应用规则R 3(resp.,R 4),对象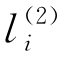 被发送出膜r并进化为l j(resp.,l k)。需要注意的是,膜4中对象l j(resp.,l k)的出现独立于以上指令集合中所有规则的执行时间。
被发送出膜r并进化为l j(resp.,l k)。需要注意的是,膜4中对象l j(resp.,l k)的出现独立于以上指令集合中所有规则的执行时间。
(2)对于每条减法指令l i:(SUB(r),l j,l k),r=1、2、3,指令集合I构造如下:
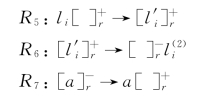
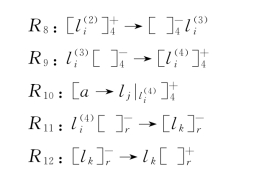
下面模拟减法指令li。系统在某一步应用规则R5,对象li进入相应的膜r中,并进化为对象![]() ,然后执行规则R6将该对象送出所在的膜并进化为
,然后执行规则R6将该对象送出所在的膜并进化为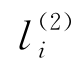 ,同时将该膜上的电荷从正变为负。下面可能会出现以下两种情况:
,同时将该膜上的电荷从正变为负。下面可能会出现以下两种情况:
(1)当对减法指令li开始模拟时,在膜r中至少存在一个对象a。对于这种情况,当规则R6执行结束时,规则R7和R8同时开始执行。这时,由于对应膜r的膜上电荷为负,通过应用规则R7将一份对象a送出该膜,并将该膜上的电荷从负变为正。这样,一份对象a会在膜r中被消耗。另外,通过执行规则R8,对象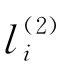 被送出膜4并进化为
被送出膜4并进化为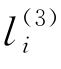 ,并将该膜的膜上电荷从正变为负。规则R8应用结束后,启动规则R9,对象
,并将该膜的膜上电荷从正变为负。规则R8应用结束后,启动规则R9,对象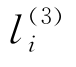 进入膜4并进化为
进入膜4并进化为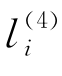 ,将该膜的膜上电荷重新变为正。当对象
,将该膜的膜上电荷重新变为正。当对象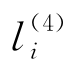 出现在膜4中,并且规则R7执行结束时,将
出现在膜4中,并且规则R7执行结束时,将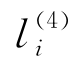 作为促进剂,在该促进剂的作用下,通过应用规则R10将对象a进化为lj,系统开始模拟指令lj。在该过程中,膜4中对象lj的出现独立于规则R7、R8、R9和R10的执行时间。
作为促进剂,在该促进剂的作用下,通过应用规则R10将对象a进化为lj,系统开始模拟指令lj。在该过程中,膜4中对象lj的出现独立于规则R7、R8、R9和R10的执行时间。
(2)当对减法指令li开始模拟时,膜r中不存在对象a。在这种情况下,规则R8和R9将先后开始执行,最终对象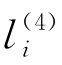 出现在膜4中。此时,通过执行规则R11,对象
出现在膜4中。此时,通过执行规则R11,对象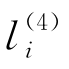 进入膜r中,进化为对象lk。当对象lk出现在膜r中时,规则R12开始执行,lk被送出膜r,并将该膜的膜上电荷重新变为正,系统开始模拟指令lk。膜4中对象lk的出现独立于规则R8、R9、R11和R12的执行时间。
进入膜r中,进化为对象lk。当对象lk出现在膜r中时,规则R12开始执行,lk被送出膜r,并将该膜的膜上电荷重新变为正,系统开始模拟指令lk。膜4中对象lk的出现独立于规则R8、R9、R11和R12的执行时间。
因此,系统可以正确地模拟M中的加法指令和减法指令。最后,系统将停止计算,这时,对象lh出现在膜4中。系统即使在时间无关模式下工作,依然能够得到正确的结果,这样的系统具有较好的鲁棒性和容错性。
本章通过仅带两类电荷并且使用促进剂的时间活性膜P系统求解了SAT问题。如果将膜上的电荷去除,可以考虑该系统是否还能求解NP完全问题。另外,使用该膜系统求解PSPACE完全问题的计算效率还有待进一步研究。
